Complete Solutions to Linked Comprehension of chapter FLUID MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FLUID MECHANICS |
| CENGAGE PHYSICS | Linked Comprehension |
| Number Of Questions | 43 |
| Academic Year | 2023-24 |
A small spherical ball of radius `r` is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height `h` (measured from the bottom) as `rho_(L)=rho_(0)[4-(3h//h_(0))]`.The density of the ball is (`5//2)rho_(0)`. The height of the vessel is `h_(0)=12//pi^(2)` Consider `r lt lt h_(0)` and `g = 10 m//s^(2)`.

The motion of the ball in the vessel is
View SolutionA small spherical ball of radius `r` is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height `h` (measured from the bottom) as `rho_(L)=rho_(0)[4-(3h//h_(0))]`.The density of the ball is (`5//2)rho_(0)`. The height of the vessel is `h_(0)=12//pi^(2)` Consider `r lt lt h_(0)` and `g = 10 m//s^(2)`.

The ball will reach at the bottom of the vessel
View SolutionA cylindrical tank having cross-sectional area `A = 0.5 m^(2)` is filled with two liquids of density `rho_(1)=900 kg m^(-3)` and `rho_(2)=600 kgm^(-3)`, to a height `h=60cm` each as shown in the figure. A small hole having area `a=5cm^(2)` is made in right vertical wall at a height `y = 20 cm` from the bottom. A horizontal force `F` is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (`ake `g = 10 ms^(-2)`).
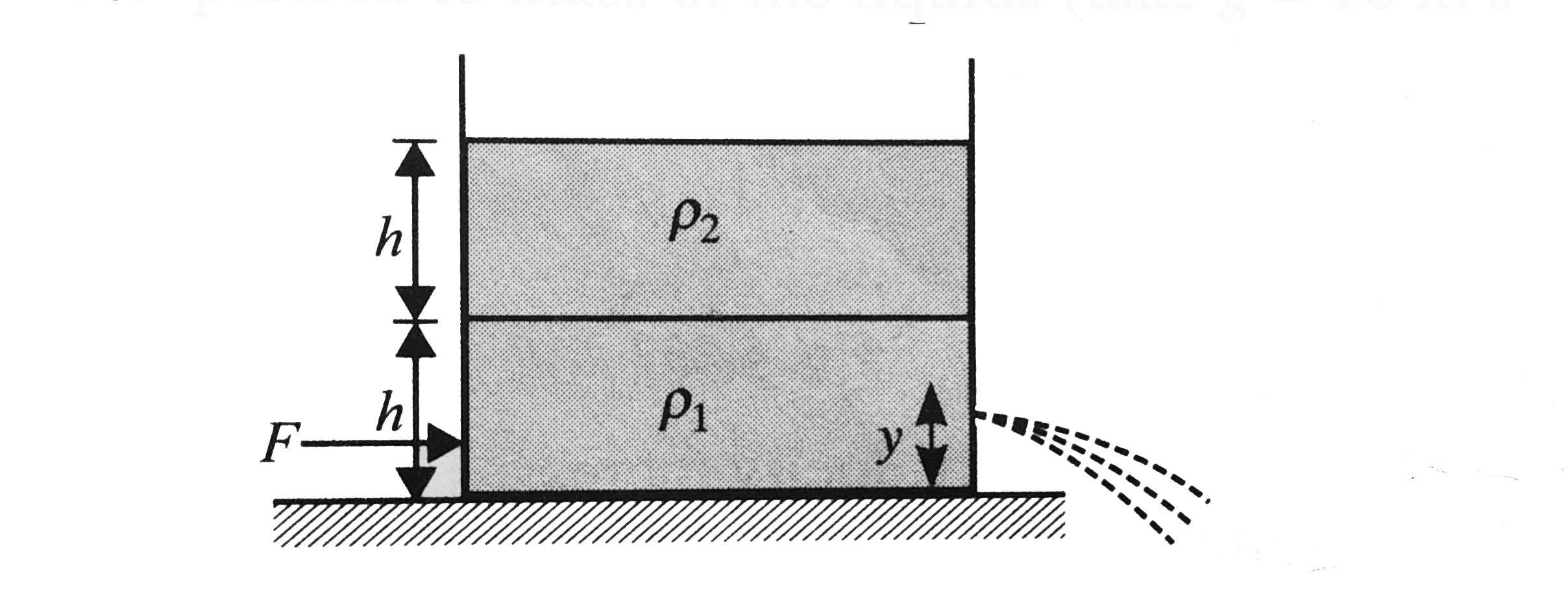
The velocity of efflux is
View SolutionA cylindrical tank having cross-sectional area `A = 0.5 m^(2)` is filled with two liquids of density `rho_(1)=900 kg m^(-3)` and `rho_(2)=600 kgm^(-3)`, to a height `h=60cm` each as shown in the figure. A small hole having area `a=5cm^(2)` is made in right vertical wall at a height `y = 20 cm` from the bottom. A horizontal force `F` is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (`ake `g = 10 ms^(-2)`).
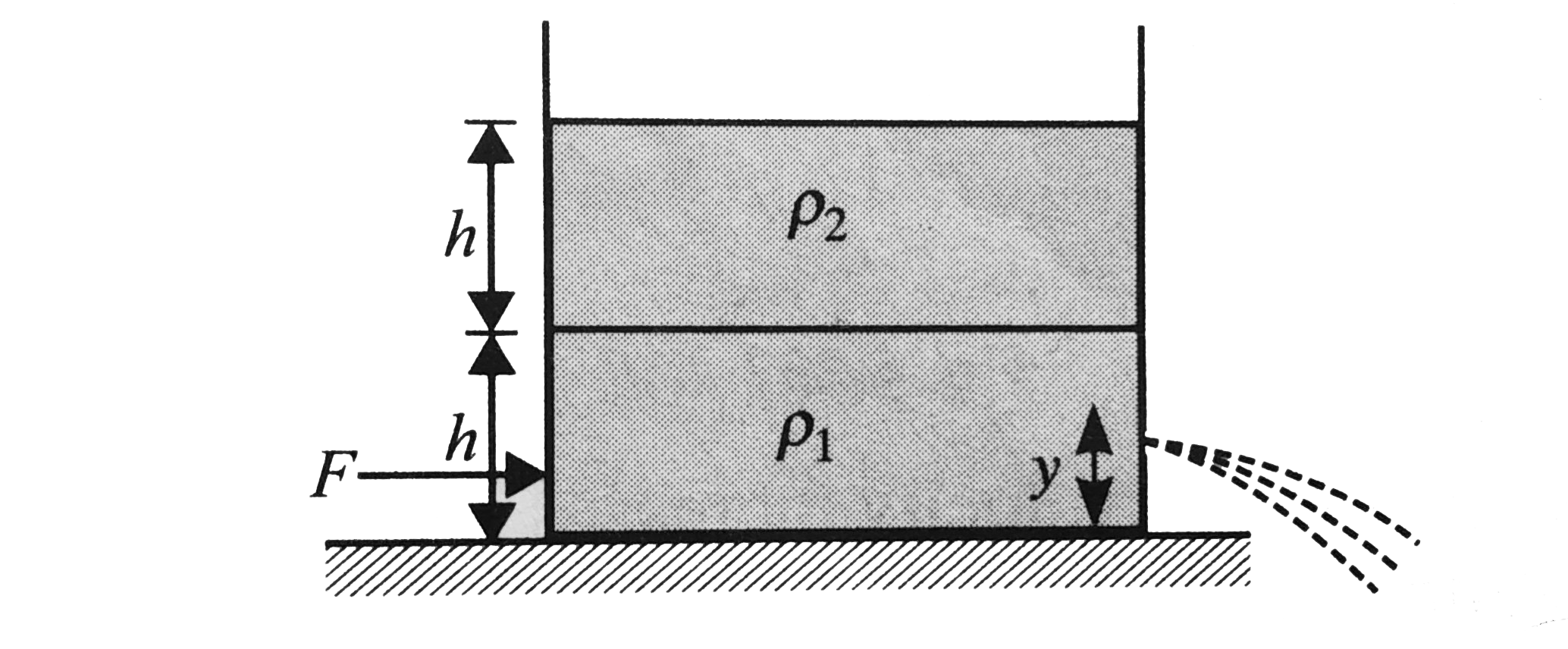
The velocity of efflux is
View SolutionA cylindrical tank having cross-sectional area `A = 0.5 m^(2)` is filled with two liquids of density `rho_(1)=900 kg m^(-3)` and `rho_(2)=600 kgm^(-3)`, to a height `h=60cm` each as shown in the figure. A small hole having area `a=5cm^(2)` is made in right vertical wall at a height `y = 20 cm` from the bottom. A horizontal force `F` is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (`ake g = 10 ms^(-2)`).
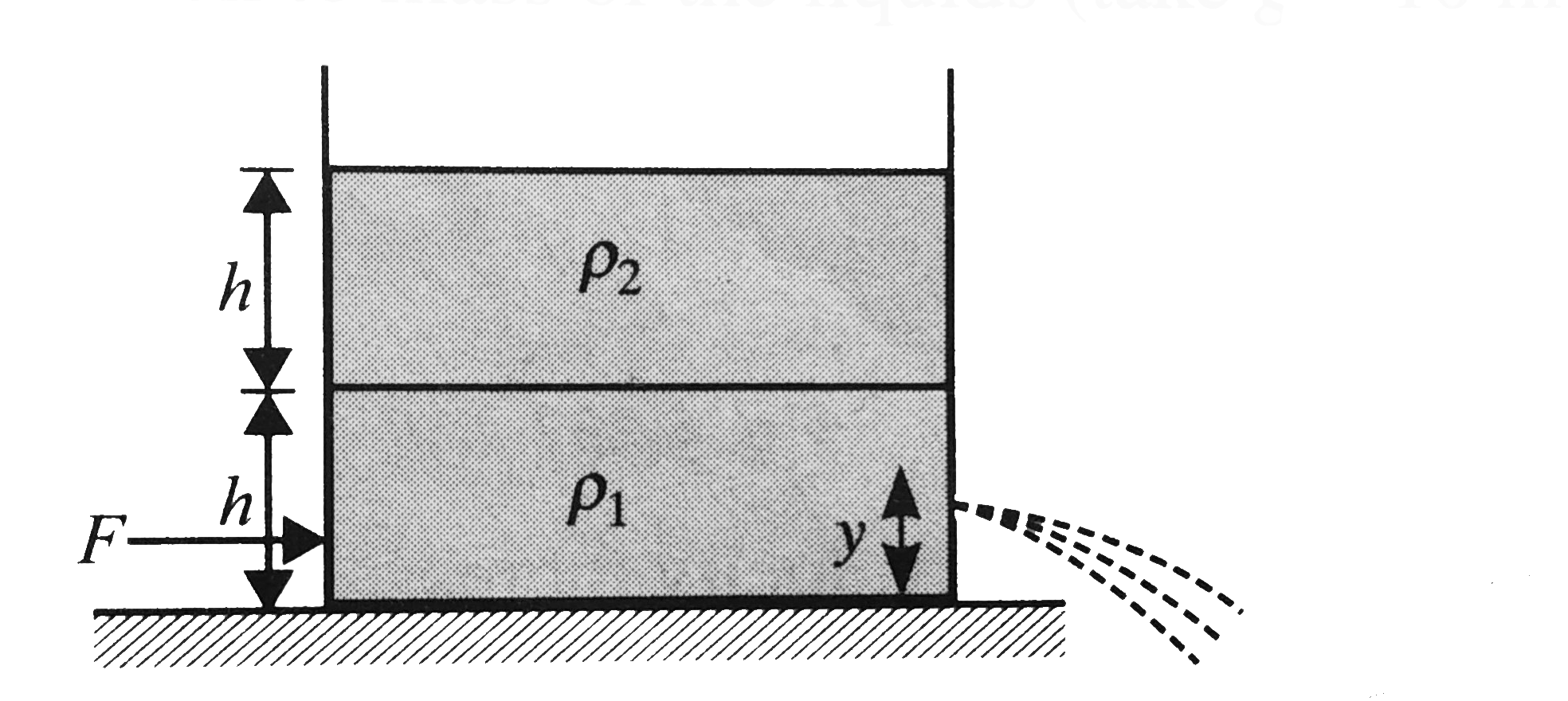
The velocity of efflux is
View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height `h_(0)` and pressure `2p_(0)` where `rh_(0)` is the atmospheric pressure. There is a hole in the wall of the tank at a depth `h_(1)` below the top from which water comes out. A long vertical tube is connected as shown.

Find the height `h_(2)` of the water in the long tube above top initially.
View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height `h_(0)` and pressure `2p_(0)` where `rh_(0)` is the atmospheric pressure. There is a hole in the wall of the tank at a depth `h_(1)` below the top from which water comes out. A long vertical tube is connected as shown.

Find the speed with which water comes out of the hole
View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height `h_(0)` and pressure `2p_(0)` where `rh_(0)` is the atmospheric pressure. There is a hole in the wall of the tank at a depth `h_(1)` below the top from which water comes out. A long vertical tube is connected as shown.

Find the height of the water in the long tube above the top when the water stops coming out of the hole.
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (`a_(y)`) for calculation of pressure, effective `g` is used. A closed box horizontal base `6 m` by `6 m` and a height `2m` is half filled with liquid. It is given a constant horizontal acceleration `g//2` and vertical downward acceleration `g//2`.
The angle of the free surface with the horizons is equal to
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (`a_(y)`) for calculation of pressure, effective `g` is used. A closed box horizontal base `6 m` by `6 m` and a height `2m` is half filled with liquid. It is given a constant horizontal acceleration `g//2` and vertical downward acceleration `g//2`.
Length of exposed portion of top of box is equal to
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (`a_(y)`) for calculation of pressure, effective `g` is used. A closed box horizontal base `6 m` by `6 m` and a height `2m` is half filled with liquid. It is given a constant horizontal acceleration `g//2` and vertical downward acceleration `g//2`.
Water pressure at the bottomof centre of the box is equal to (atmospheric pressure `=10^(5)N//m^(2)` density of water `=1000 kg//m^(3),g=10m//s^(2)`)
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (`a_(y)`) for calculation of pressure, effective `g` is used. A closed box horizontal base `6 m` by `6 m` and a height `2m` is half filled with liquid. It is given a constant horizontal acceleration `g//2` and vertical downward acceleration `g//2`.
The maximum value of water pressure in the box is equal to
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (`a_(y)`) for calculation of pressure, effective `g` is used. A closed box horizontal base `6 m` by `6 m` and a height `2m` is half filled with liquid. It is given a constant horizontal acceleration `g//2` and vertical downward acceleration `g//2`.
What is the value of vertical acceleration of box for given horizontal acceleration `(g//2)`, so that no part of the bottom of the box is exposed?
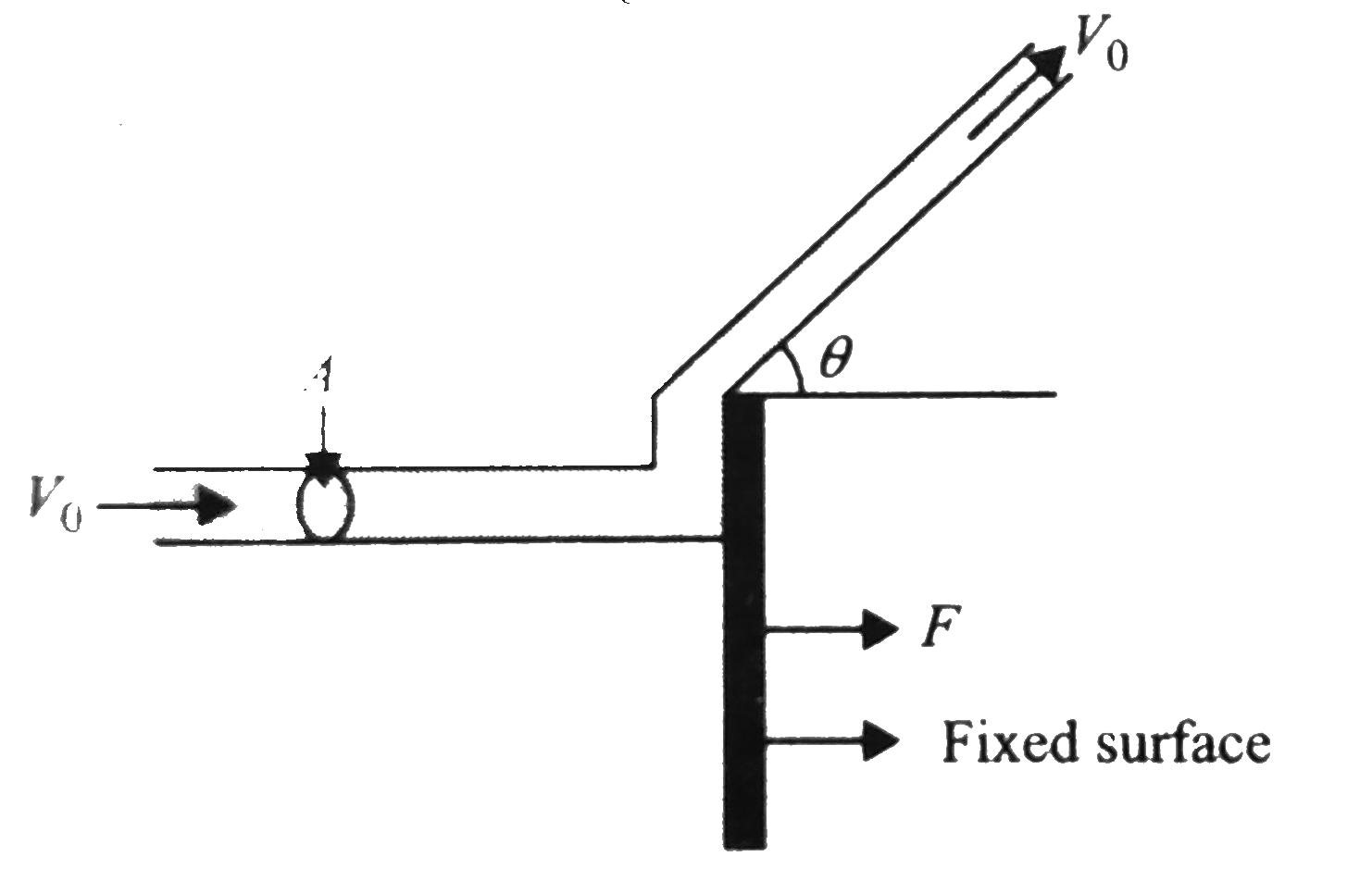
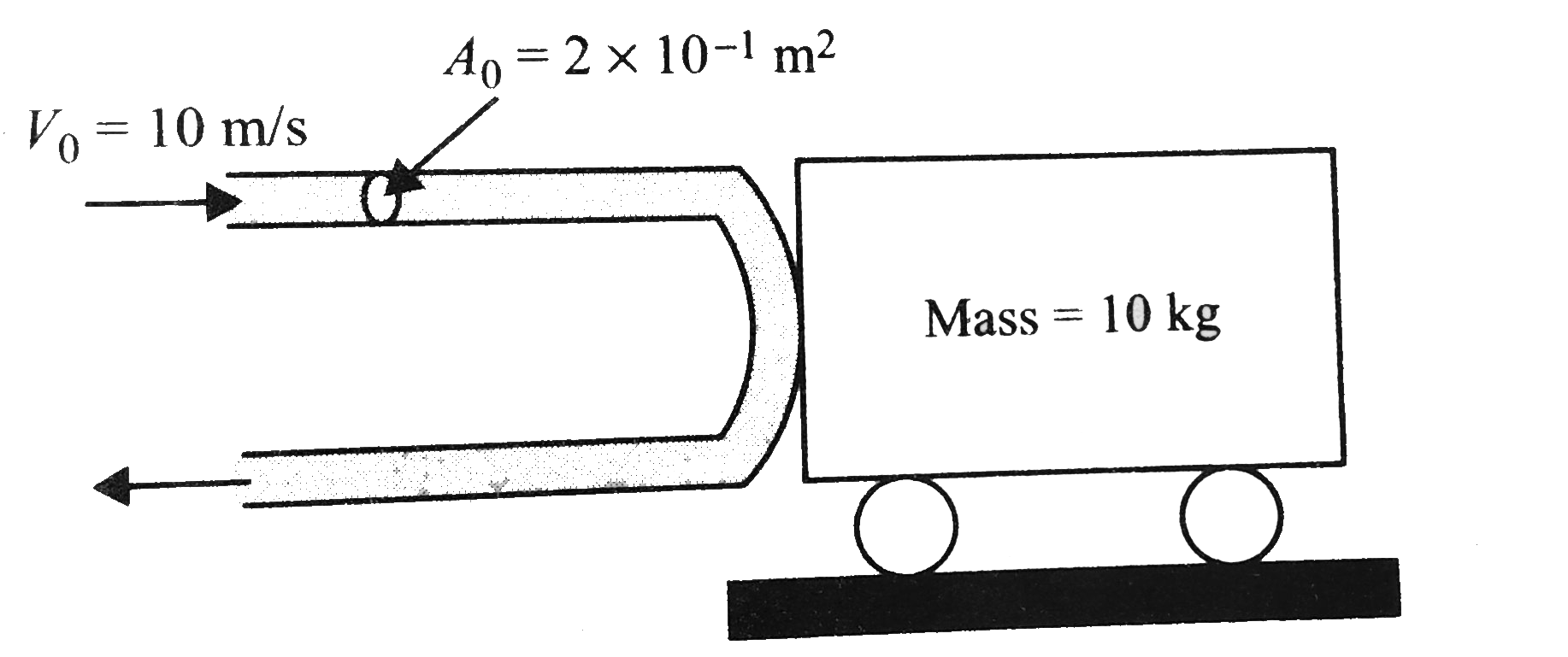
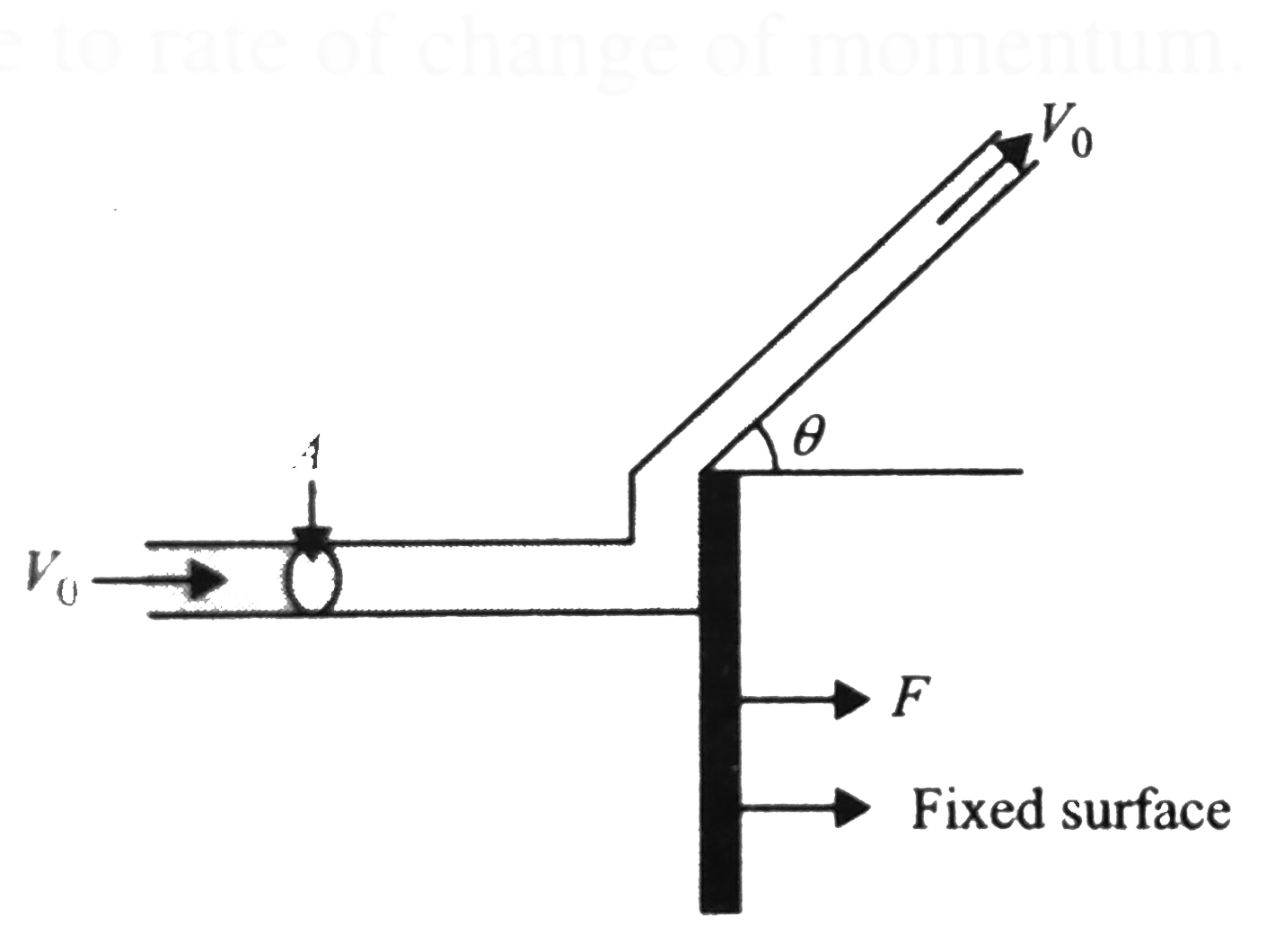
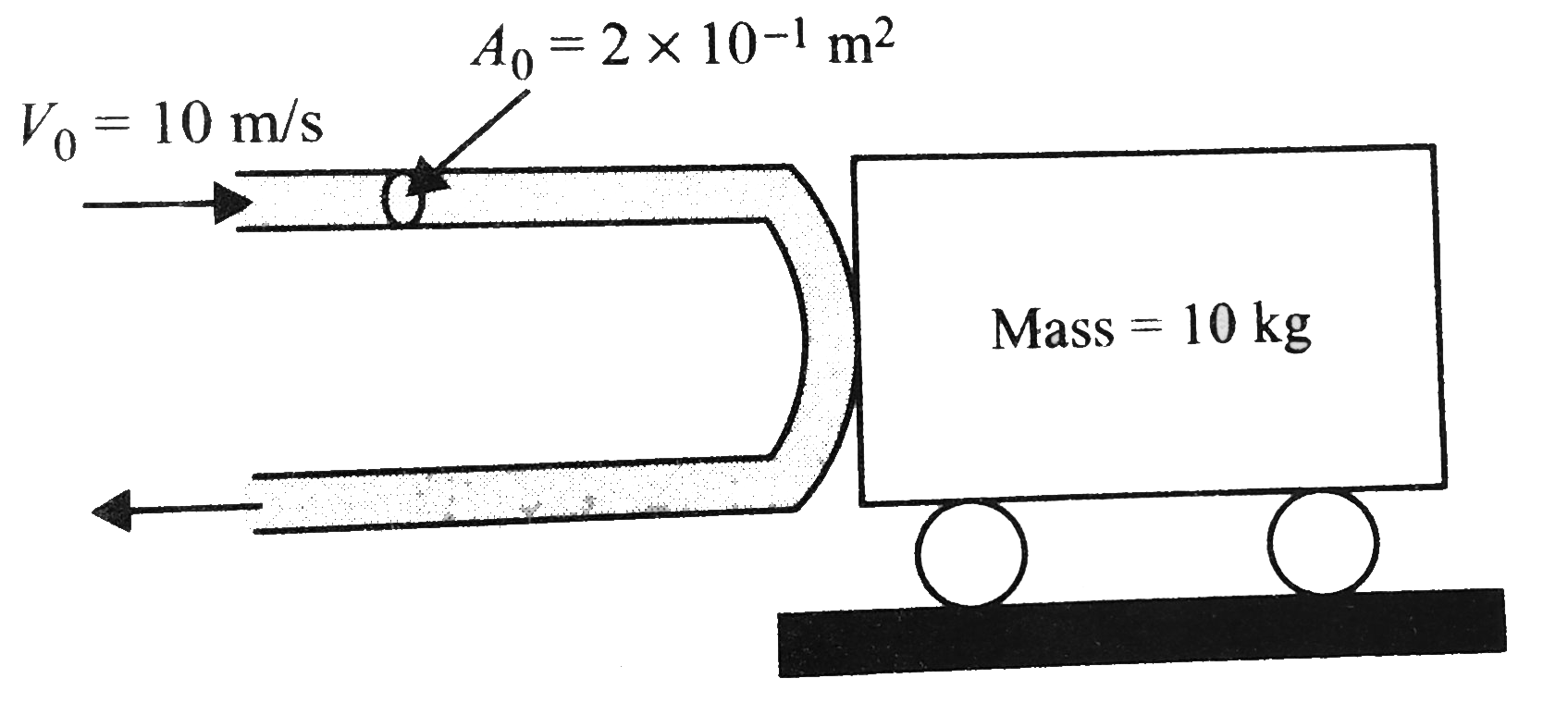
View SolutionWhen a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
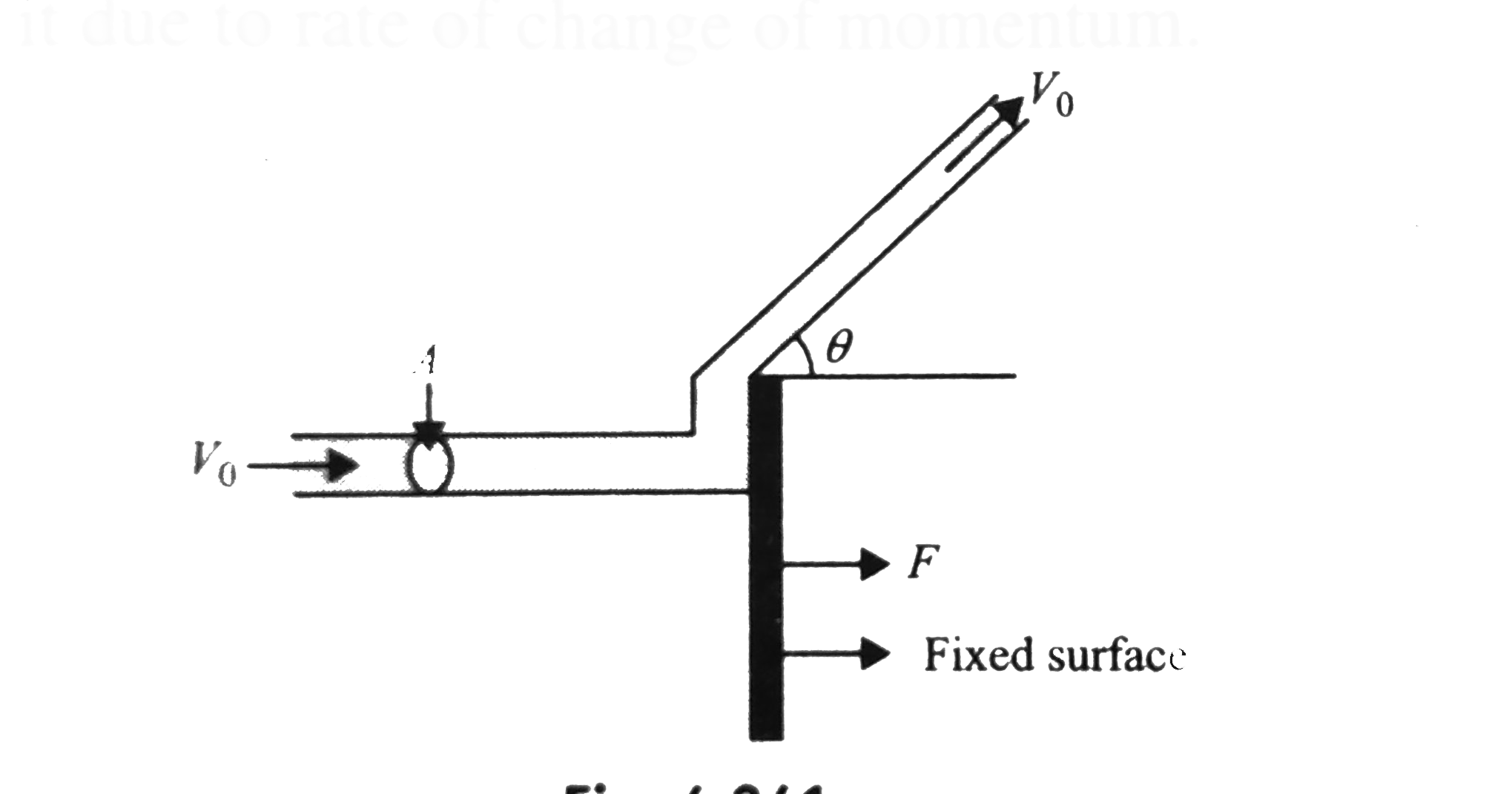
`F=(rhoAV_(0))V_(0)-(rhoAV_(0))V_(0)costheta=rhoAV_(0)^(2)[1-costheta]` If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be `u`. Then the above equation becomes `
F=rhoA(V_(0)-u)^(2)[1-costheta]` Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
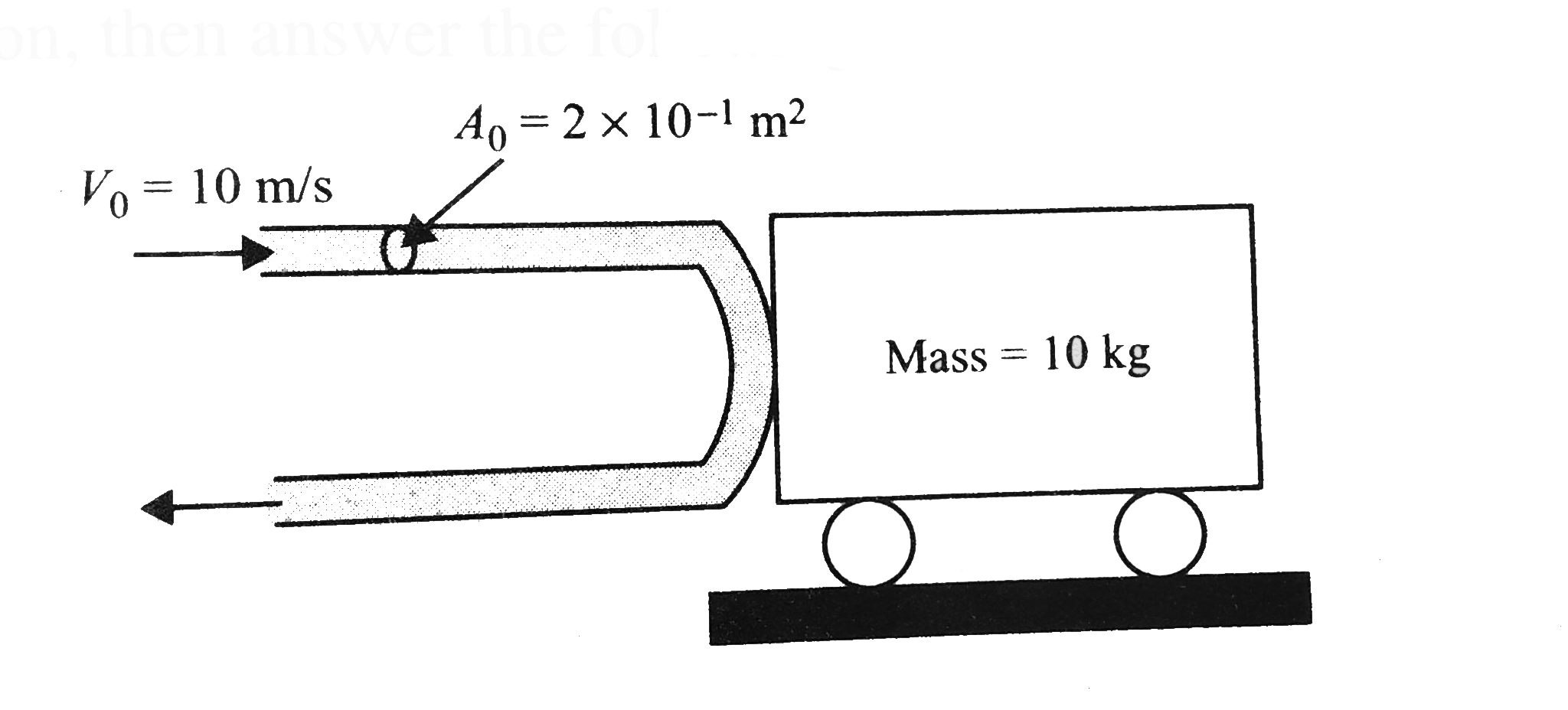
Given that cross sectional area of jet `=2xx10^(-4)m^(2)` velocity of jet `V_(0)=10m//s` density of liquid `=1000kg//m^(3)` ,mass of cart `M=10 kg`.
Initially (`l=0`) the force on the cart is equal to
View SolutionWhen a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
`F=(rhoAV_(0))V_(0)-(rhoAV_(0))V_(0)costheta=rhoAV_(0)^(2)[1-costheta]` If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be `u`. Then the above equation becomes `
F=rhoA(V_(0)-u)^(2)[1-costheta]` Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
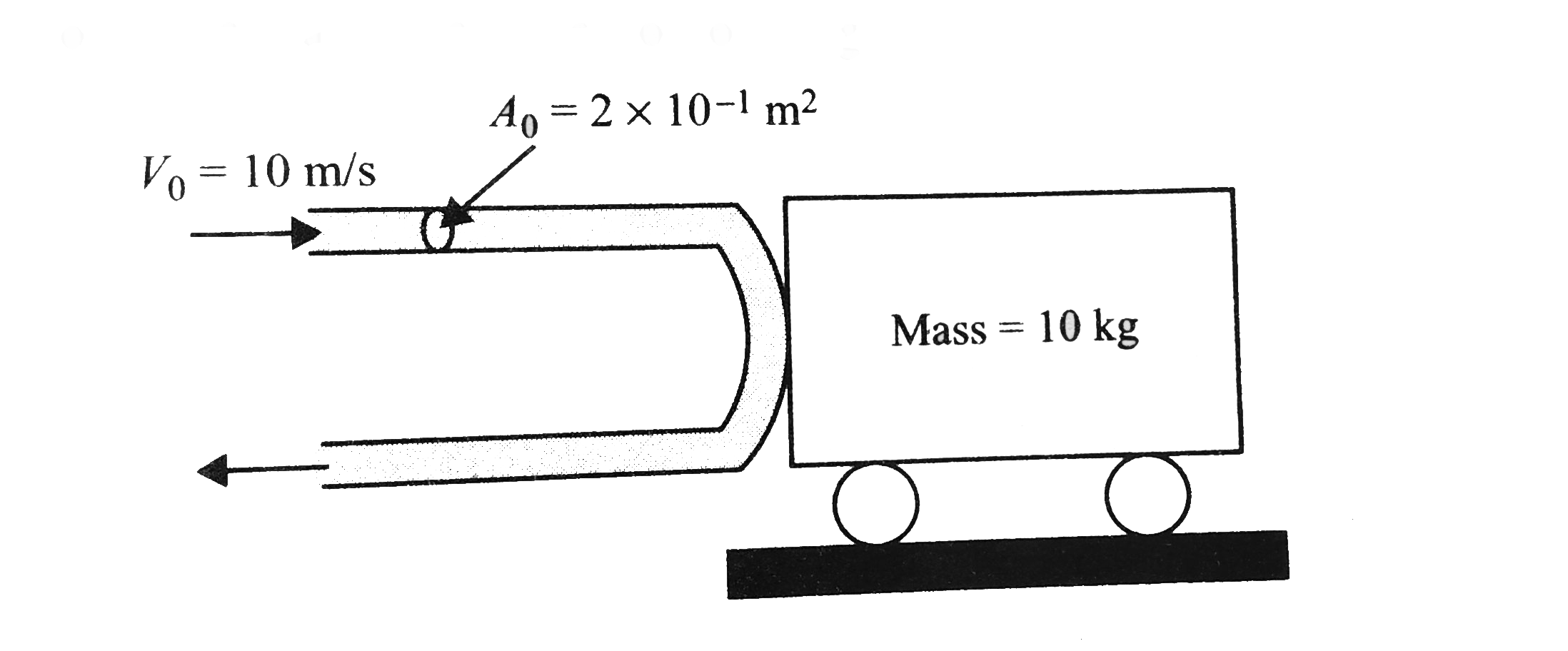
Given that cross sectional area of jet `=2xx10^(-4)m^(2)` velocity of jet `V_(0)=10m//s` density of liquid `=1000kg//m^(3)` ,mass of cart `M=10 kg`.
Velocity of cart at `t = 10 s` is equal to
View SolutionWhen a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
`F=(rhoAV_(0))V_(0)-(rhoAV_(0))V_(0)costheta=rhoAV_(0)^(2)[1-costheta]` If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be `u`. Then the above equation becomes `
F=rhoA(V_(0)-u)^(2)[1-costheta]` Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
Given that cross sectional area of jet `=2xx10^(-4)m^(2)` velocity of jet `V_(0)=10m//s` density of liquid `=1000kg//m^(3)` ,mass of cart `M=10 kg`.
The time at which velocity of cart becomes `2 m/s` is equal to
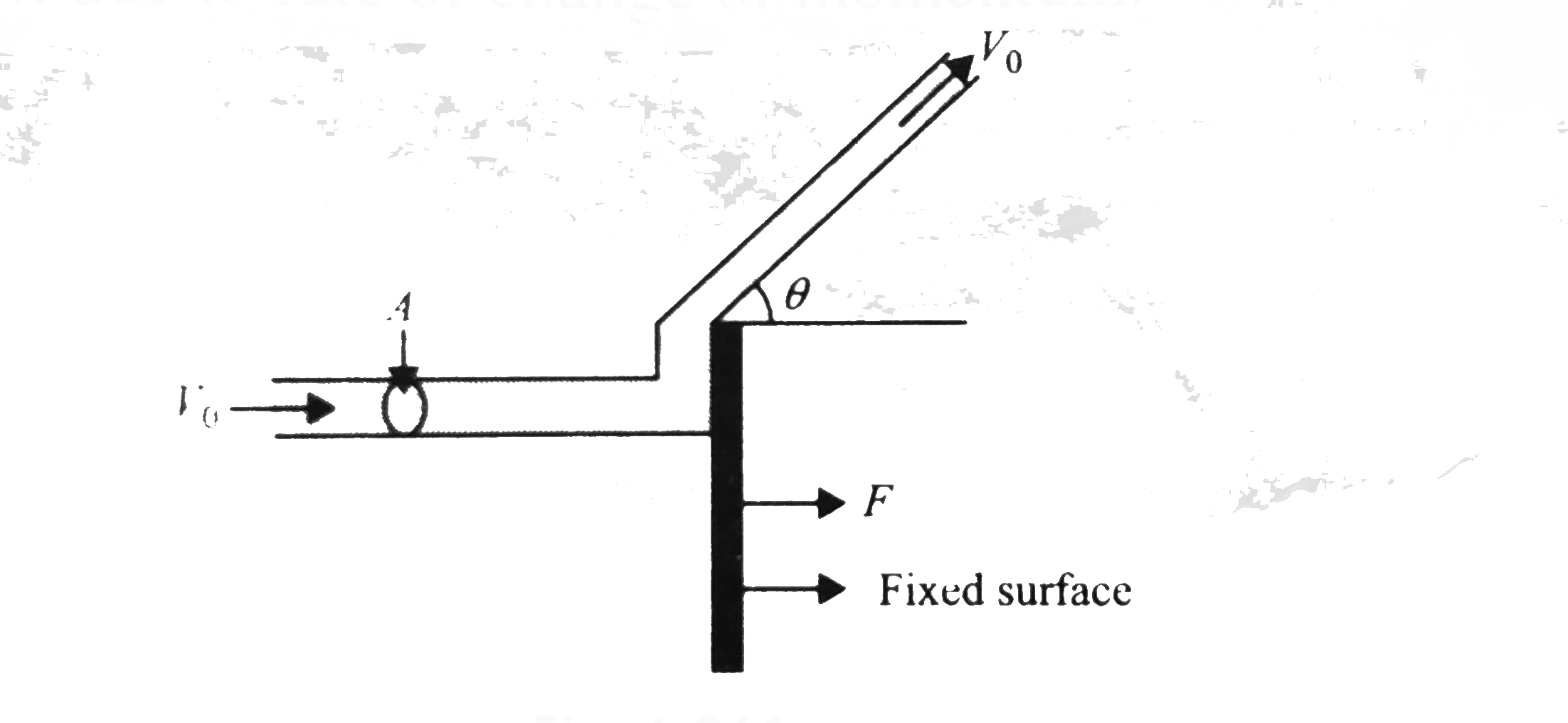
View SolutionWhen a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
`F=(rhoAV_(0))V_(0)-(rhoAV_(0))V_(0)costheta=rhoAV_(0)^(2)[1-costheta]` If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be `u`. Then the above equation becomes `
F=rhoA(V_(0)-u)^(2)[1-costheta]` Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
Given that cross sectional area of jet `=2xx10^(-4)m^(2)` velocity of jet `V_(0)=10m//s` density of liquid `=1000kg//m^(3)` ,mass of cart `M=10 kg`.
The power supplied to the cart when its velocity becomes `5 m//s` is equal to
View SolutionA uniform rod of length `L` pivoted at the bottom of a pond of depth `L//2` stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.
View SolutionA uniform rod of length `L` pivoted at the bottom of a pond of depth `L//2` stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass `m` of the rod.
View SolutionA cylindrical object of cork of mass `15 g` and cross-sectional area `A_(1) = 10 cm^(2)` floats in a pan of water as shown in the figure. An aluminum, cylinder of mass `25 g` and cross-sectional area `A_(2) = 2 cm^(2)` is attached `4 cm` below the cork and slides through a watertight frictionless hole in the bottom of the pan. Take density of the cork, `rho = 0.2 g//cm^(3), rho_("aluminium") = 2.7 g//cm^(3), g = 10 m//s^(2)`. Based on the above information, answer the following questions.

The length of the cork cylinder inside the water in equilibrium is
View SolutionA cylindrical object of cork of mass `15 g` and cross-sectional area `A_(1) = 10 cm^(2)` floats in a pan of water as shown in the figure. An aluminum, cylinder of mass `25 g` and cross-sectional area `A_(2) = 2 cm^(2)` is attached `4 cm` below the cork and slides through a watertight frictionless hole in the bottom of the pan. Take density of the cork, `rho = 0.2 g//cm^(3), rho_("aluminium") = 2.7 g//cm^(3), g = 10 m//s^(2)`. Based on the above information, answer the following questions.
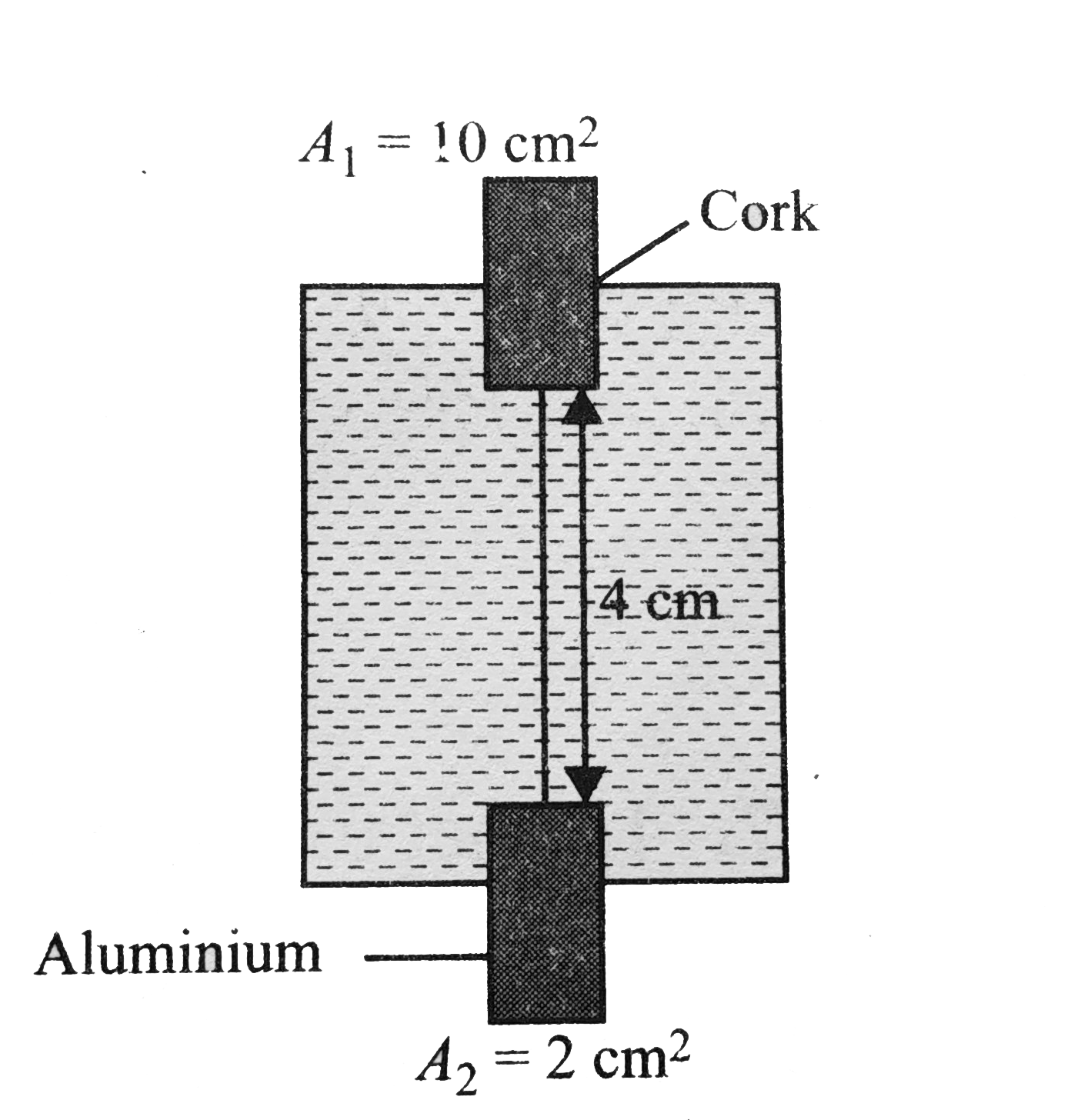
The tension in the string joining the cork and aluminium cylinder is
View SolutionA liquid having density `6000 kg//m^(3)` stands to a height of `4 m` in a sealed tank as shown in the figure. The tank contains compressed air at a gauge pressure of `3 atm`. The horizontal outlet pipe has a cross-sectional area of `6 cm^(2)` and `3 cm^(2)` at larger and smaller sections. Atmospheric pressure `= 1 atm, g = 10m//s^(2) 1 atm =10^(5) N//m^(2)`.

Assume that depth of water in the tank remains constant due to `s` very large base and air pressure above it remains constant. Based on the above information, answer the following questions.
The discharge rate from the outlet is
View SolutionA liquid having density `6000 kg//m^(3)` stands to a height of `4 m` in a sealed tank as shown in the figure. The tank contains compressed air at a gauge pressure of `3 atm`. The horizontal outlet pipe has a cross-sectional area of `6 cm^(2)` and `3 cm^(2)` at larger and smaller sections. Atmospheric pressure `= 1 atm, g = 10m//s^(2) 1 atm =10^(5) N//m^(2)`.
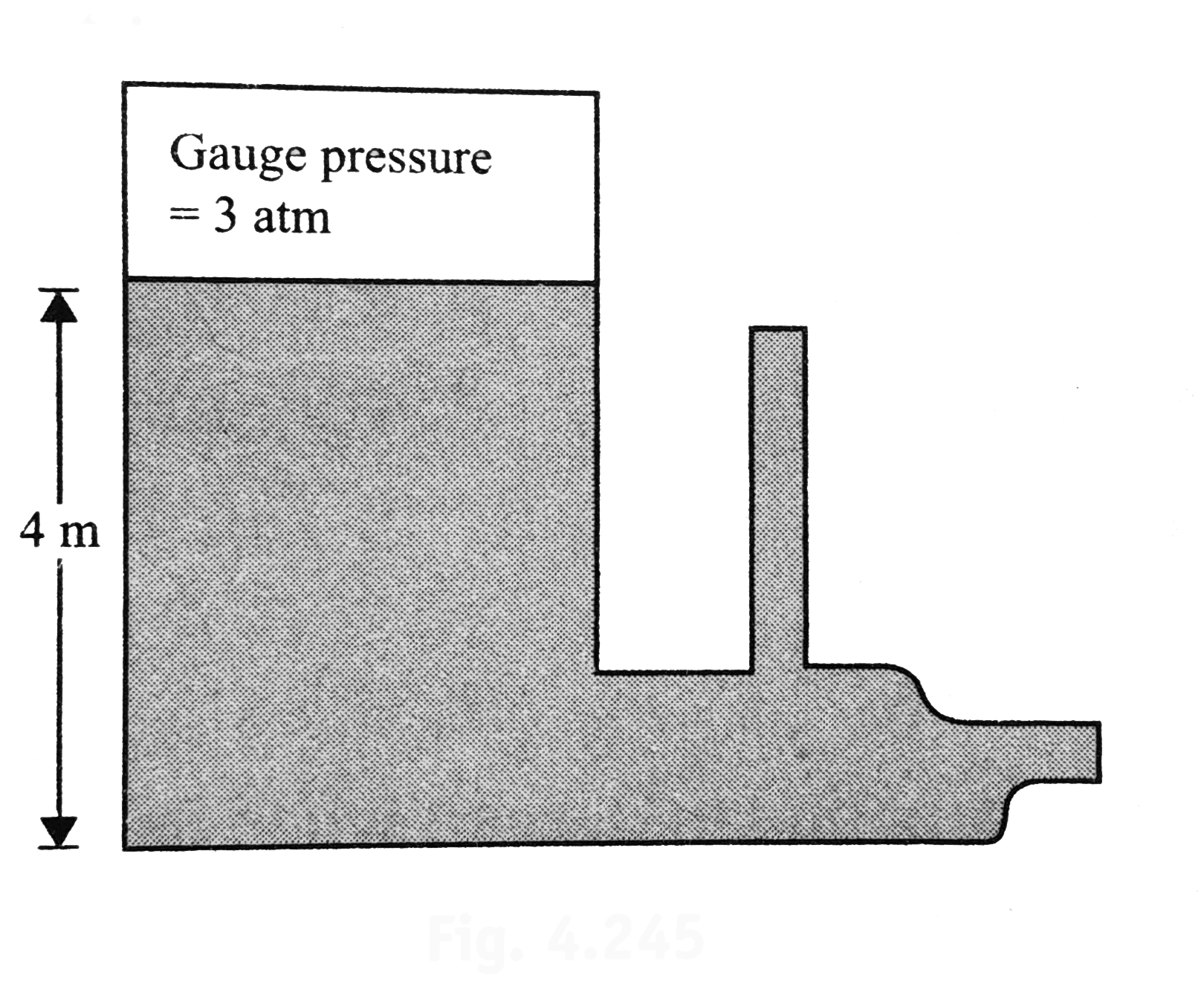
Assume that depth of water in the tank remains constant due to `s` very large base and air pressure above it remains constant. Based on the above information, answer the following questions.
The height at which liquid will stand in the open end of the pipe is
View SolutionA liquid having density `6000 kg//m^(3)` stands to a height of `4 m` in a sealed tank as shown in the figure. The tank contains compressed air at a gauge pressure of `3 atm`. The horizontal outlet pipe has a cross-sectional area of `6 cm^(2)` and `3 cm^(2)` at larger and smaller sections. Atmospheric pressure `= 1 atm, g = 10m//s^(2) 1 atm =10^(5) N//m^(2)`.

Assume that depth of water in the tank remains constant due to `s` very large base and air pressure above it remains constant. Based on the above information, answer the following questions.
The height at which liquid will stand in the open end of the pipe is
View SolutionThe vessel shown in the figure contains water, take `rho_("water")=1000kg//m^(2), g=m//s^(2)`). For this arrangement, answer the following questions:
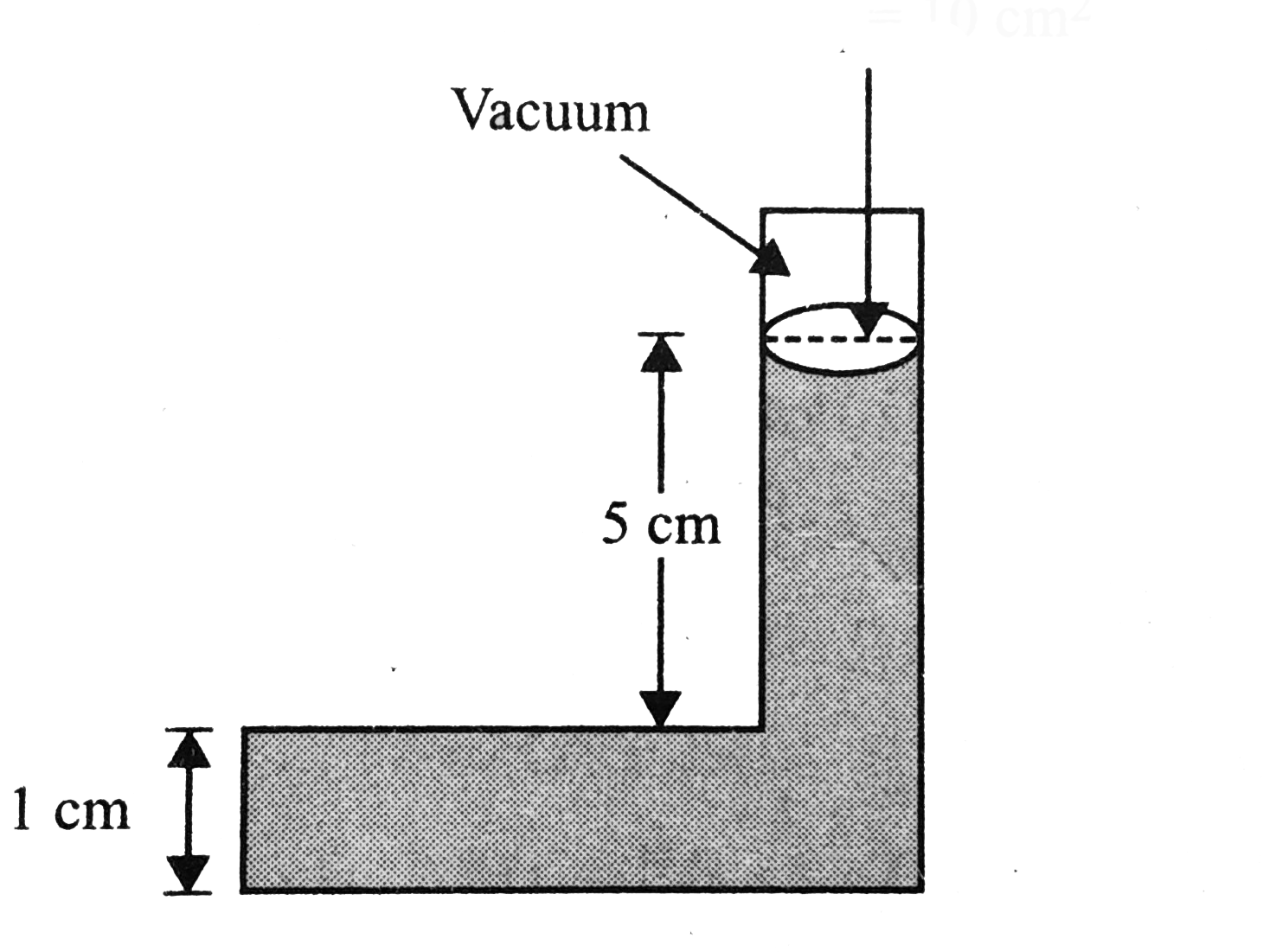
The net force acting on the base of the vessel is
View SolutionThe vessel shown in the figure contains water, take `rho_("water")=1000kg//m^(2), g=m//s^(2)`). For this arrangement, answer the following questions:
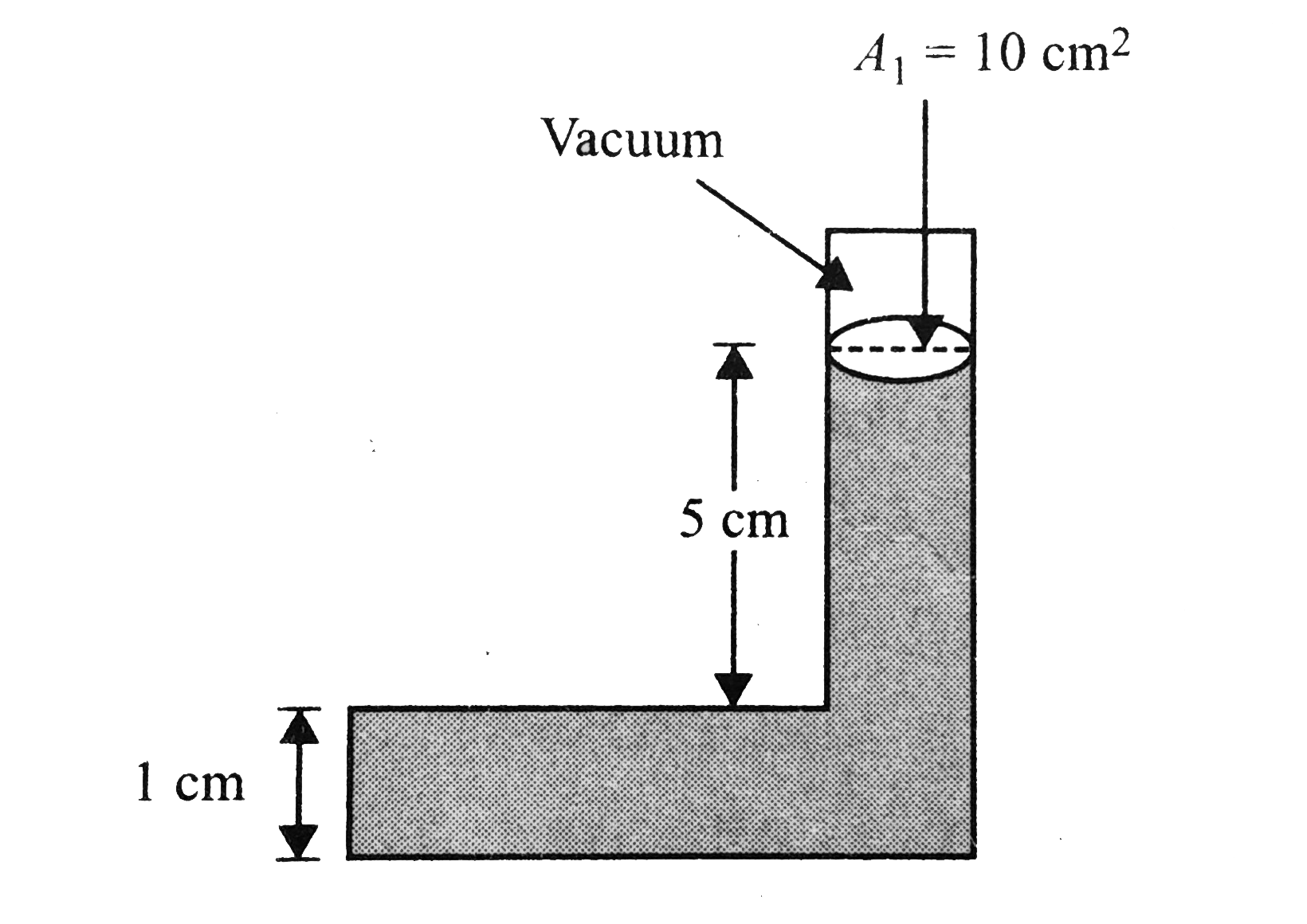
Mark out the correct statement(s).
View SolutionA rod of length `6m` has a mass of `12 kg`. It is hinged at one end of the rod at a distance of `3m` below the water surface.
a.What must be the weight of a block that is attached to the other end of the rod so that `5 m` of the rod's length is under water?
b. Find the magnitude and direction of the force exerted by the hinge on the rod. The specific gravity of the material of rod is `0.5.`

View SolutionA rod of length `6m` has a mass of `12 kg`. It is hinged at one end of the rod at a distance of `3m` below the water surface.
a.What must be the weight of a block that is attached to the other end of the rod so that `5 m` of the rod's length is under water?
b. Find the magnitude and direction of the force exerted by the hinge on the rod. The specific gravity of the material of rod is `0.5.`

View SolutionA tube of uniform cross section is used to siphon water from a vessel `V` as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure `(P_(0))`. The height of the tube above and below the water level in the vessel are `h_(1)` and `h_(2)`, respectively.

Determine the velocity `v_(B)` of the water issuing out at `B`.
View SolutionA tube of uniform cross section is used to siphon water from a vessel `V` as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure `(P_(0))`. The height of the tube above and below the water level in the vessel are `h_(1)` and `h_(2)`, respectively.
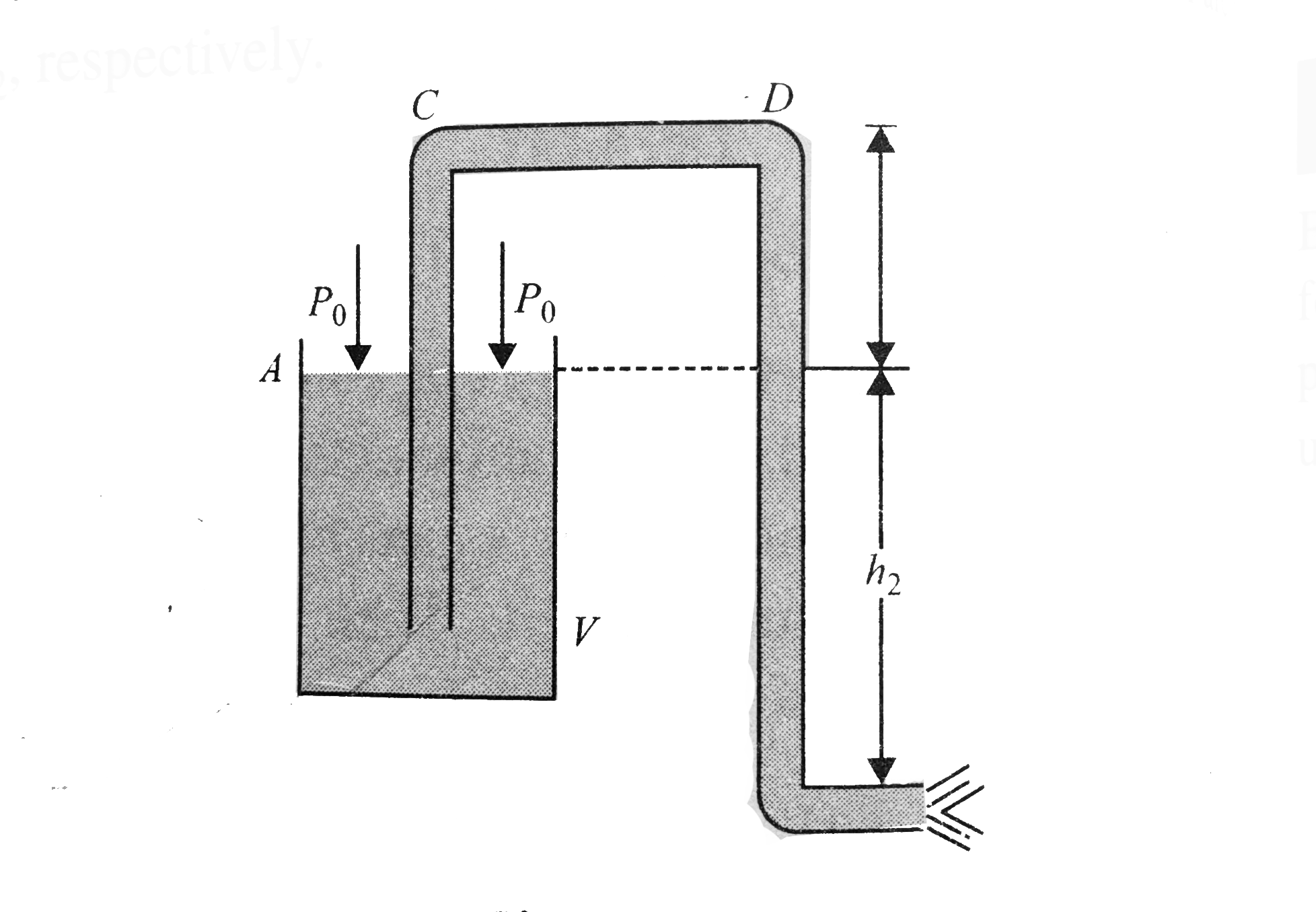
If `h_(1)=h_(2) = 3.0 m`, the maximum value of `h_(1)`, for which the siphon will work will be
View SolutionA tube of uniform cross section is used to siphon water from a vessel `V` as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure `(P_(0))`. The height of the tube above and below the water level in the vessel are `h_(1)` and `h_(2)`, respectively.
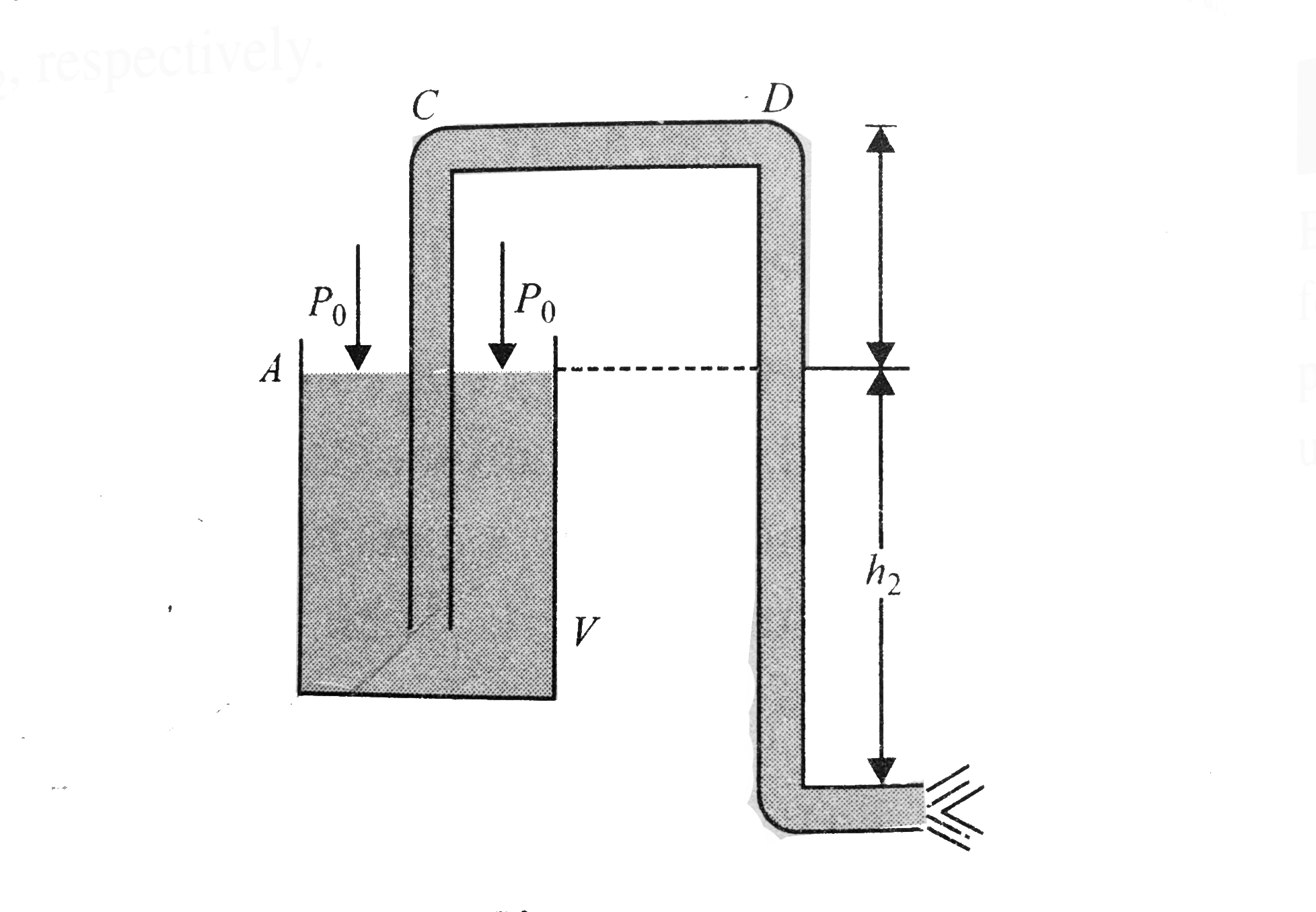
Given `h_(1) = h_(2) = 3.0 m`, the gauge pressure of water in the highest level `CD` of the tube will be
View SolutionA body of density `rho` is dropped from rest from height h (from the surface of water) into a lake of density of water `sigma(sigmagt rho)`. Neglecting all disspative effects, the acceleration of body while it is in the take is
View SolutionA body of density `rho` is dropped from reat from a height h into a lake of density `sigma(sigmagtrho)`. The maximum depth the body sinks inside the liquid is (neglect viscous effect of liquid)
View SolutionAn object of density `sigma(ltrho)` is dropped from rest at a height h into a liquid of density `rho` kept in a tall vertical cylindrical container. Neglect all dissipative effects and assume that there is no spilling of the liquid.
The time taken by the object to reach the starting point (from which it is dropped) is
View SolutionA vessel with a symmetrical hole in its bottom is Paste on a cart. The mass of the vessel and the cart is `1.5 kg`. With what force `F` (in `xx 10^(2)N)` should the cart be pulled that the maximum amount of water remains in the vessel. The dimensions of the vessel are as shown in the figure. Given that `b = 50 cm, c = 10 cm`, area of base `A= 40cm^(2), L = 20 cm, g = 10 m//s^(2).

View SolutionA solid cylinder of height `h` and mass `m` is floating in a liquid of density `rho` as shown in the figure. Find the acceleration of the vessel (in `m//s^(2)`) containing liquid for which the relative downward acceleration of the completely immersed cylinder w.r.t. vessel becomes equal to one-third of that of the vessel. (Take `g = 10 m//s^(2))`

View SolutionLength of horizontal arm of a uniform cross section `U`-tube is `l= 21 cm` and ends of both of the vertical arms are open to surrounding of pressure `10500 N//m^(2)`. A liquid of density `rho = 10^(3) kg//m^(3)` is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity `omega_(0) = 10 rad//s`. If length of each vertical arm is `a = 6 cm`, calculate the length of air column in the sealed arm. (in cm)

View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle `theta` that the plank makes with the vertical in the equilibrium position. (Exclude the case `theta=theta^@`)

View SolutionA rod of length `6 m` has specific gravity `rho (= 25//36)`. One end of the rod is tied to a `5 m` long rope, which in turn is tied to the floor of a pool `10 m` deep, as shown. Find the length (in `m`) of the part of rod which is out of water.

View SolutionLength of a horizontal arm of ends of both the vertical arms pressure `P_(0) = 10^(5) N//m^(2)`. A liquid of density `rho = 10^(3) kg //m^(3)` is poured in the tube such that liquid just fills the horizontal part of the tube as a shown in Fig. Now one end of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed `omega_(0)=sqrt(40//3)rad//sec`. If length of each vertical arm is `a = 1 m` and in the sealed end liquid rises to a height `y = 1//2 m`, find pressure in the sealed tube during rotation. (in `xx 10^(5) N//m^(2))`

View SolutionA piece of metal floats on mercury. The coefficient of volume expansion of metal and mercury are `gamma_1 and gamma_2`, respectively. if the temperature of both mercury and metal are increased by an amount `Delta T`, by what factor does the fraction of the volume of the metal submerged in mercury changes ?
View SolutionA horizontal pipeline carries water in a streamline flow. At a point along the pipe, where the cross- sectional area is `10cm^2`, the water velocity is `1ms^-1` and the pressure is 2000 Pa. The pressure of water at another point where the cross-sectional area is `5cm^2`, is........Pa. (Density of water `=10^3kg.m^-3`)
View SolutionA man is sitting in a boat which is floating in a pond. If the man drinks some water from the pond, the level of water in the pond decreases.
View Solution
Linked Comprehension questions and complete solutions for chapter FLUID MECHANICS of CENGAGE PHYSICS (HINGLISH) of Class 11