Complete Solutions to Illustration of chapter FLUID MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FLUID MECHANICS |
| CENGAGE PHYSICS | Illustration |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
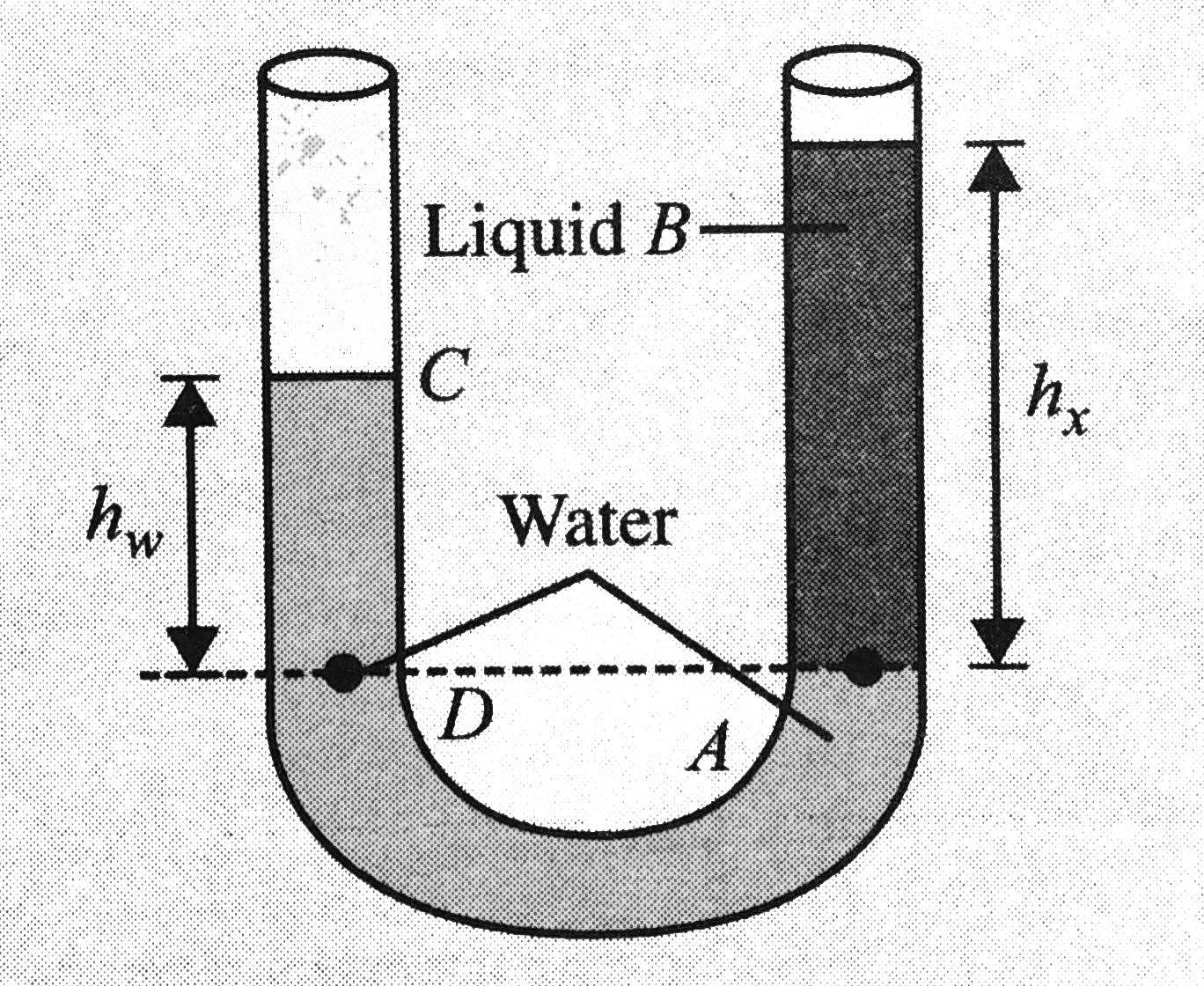
Figure shows an open tube which contains some water and a less dense liquid poured into the right hand side. If the density of the unknown liquid is `rho_(x)`, show that `rho_(x)=(rho_(w)h_(w))/(h_(x))`
View SolutionA vertical `U` tube of uniform cross section contains mercury in both of its arms. A glycerine `(d=1.3g//cm^(3))` column of length `10 cm` is introduced into one of the arms. Oil of density `0.8g//cm^(3)` is poured in the other arm until the upper surfaces of the oil and glycerine are in the same horizontal level. Find the length of oil column. Densit of mercury is `13.6g//cm^(3)`.

View SolutionTwo communicating cylindrical tubes contain mercury. The diameter of one vessel is four times large than the diameter of the outer. A column of water of height `70 cm` is poured into the narrow vessel. How much will the mercury level rise in the other vessel and how much will it sink in the narrow one? How much will the mercury level rise in the narrow vessel, if a column of water of the same height is poured into the broad vessel?

View SolutionThe area of cross section of the two arms of a hydraulic press is `1cm^(2)` and `20 cm^(2)` respectively. A force of `10 N` is applied on the water in the thinner arm. What force should be applied on the water in the thicker arms so that water may remain in equilibrium?

View SolutionIn a simple hydraulic press, the cross sectional area of the two cylinders is `5xx10^(-1)m^(2)` and `10^(-2)m^(2)` respectively. A force of `20 N` is applied at the small plunger.
a. What is the pressure produced in the cylinders?
b. What is the thrust exerted on the large plunger?
c. How much work is done by the operator, if the smaller plunger moves down `0.1m`?

View SolutionA container `A` is having some fluid of density `theta_(0)`. If is connected with a `U` tbe manometer shown in figure. Find the pressure of the container in both the cases given in figure.
View Solution_S01_019_Q01.png)
The manometer shown below is used to measure the difference in water level between the two tanks. Calculate this difference for the conditions indicated.
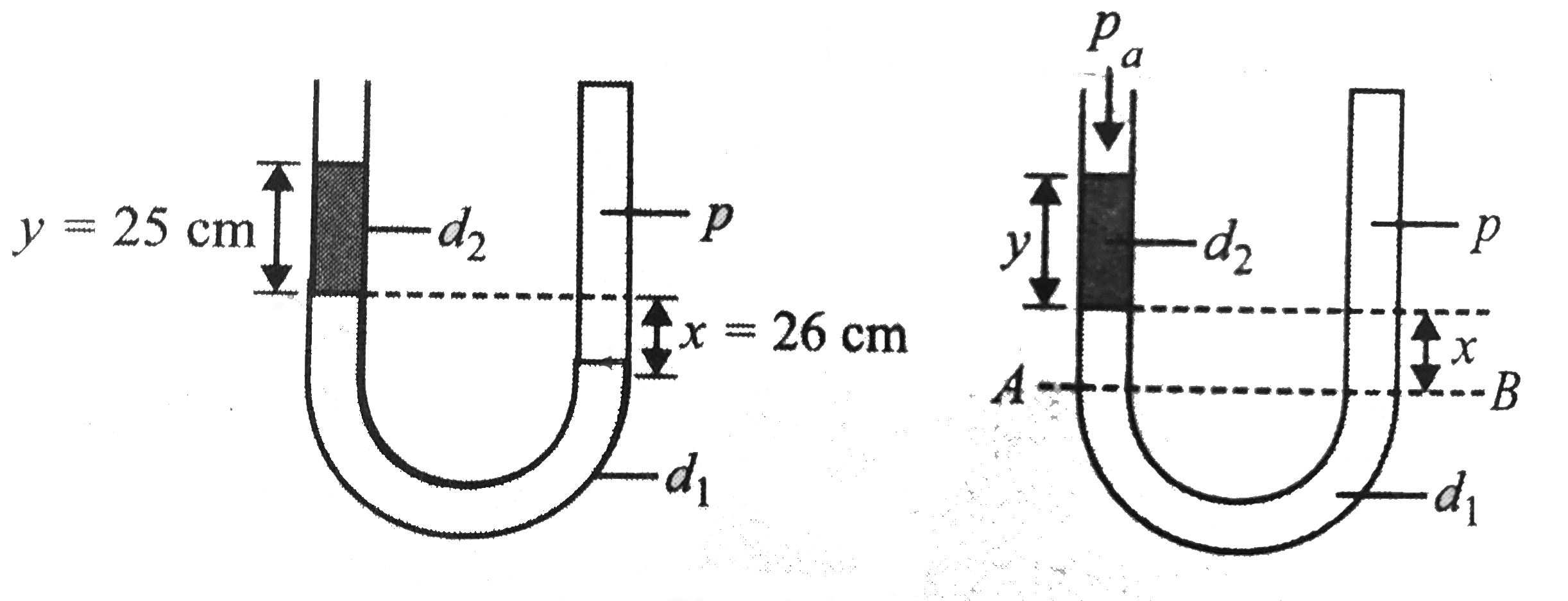
View SolutionIn a given `U` tube open at left end and closed at right end, if the pressure above the liquid the right arm is `p` find the value of `p`. Given `d_(2)=2xx13.6g//cm^(3), d_(1)=13.6g//cm^(3)`. Atmosphere pressure `p_(a)=76cm` of `Hg`.
View SolutionFind out pressures at point `A` and `B`. Also find angle `theta`. A zig zag tube open at `n`, having liquids of densities `rho_(1), rho_(2)` and `rho_(3)` is placed in a vertical plane as shown in figure. (The pressure at `M` is equal to atmospheric pressure).

View SolutionA circular tube of uniform cross section is filled with two liquids densities `rho_(1)` and `rho_(2)` such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle `theta` with horizontal find the value of `theta.`

View SolutionConsider a regular tank of size `(lxxb)` filled with a liquid of density `rho` to a height `H` as shown in figure. Find the force at the base and on the wall of the tank.

View SolutionA tank of square cross section `(2mxx2m)` is filled with water up to a height of `2.5 m`. Find the thrust experienced by the vertical and botom of the tank `(g=10m//s^(2))`.
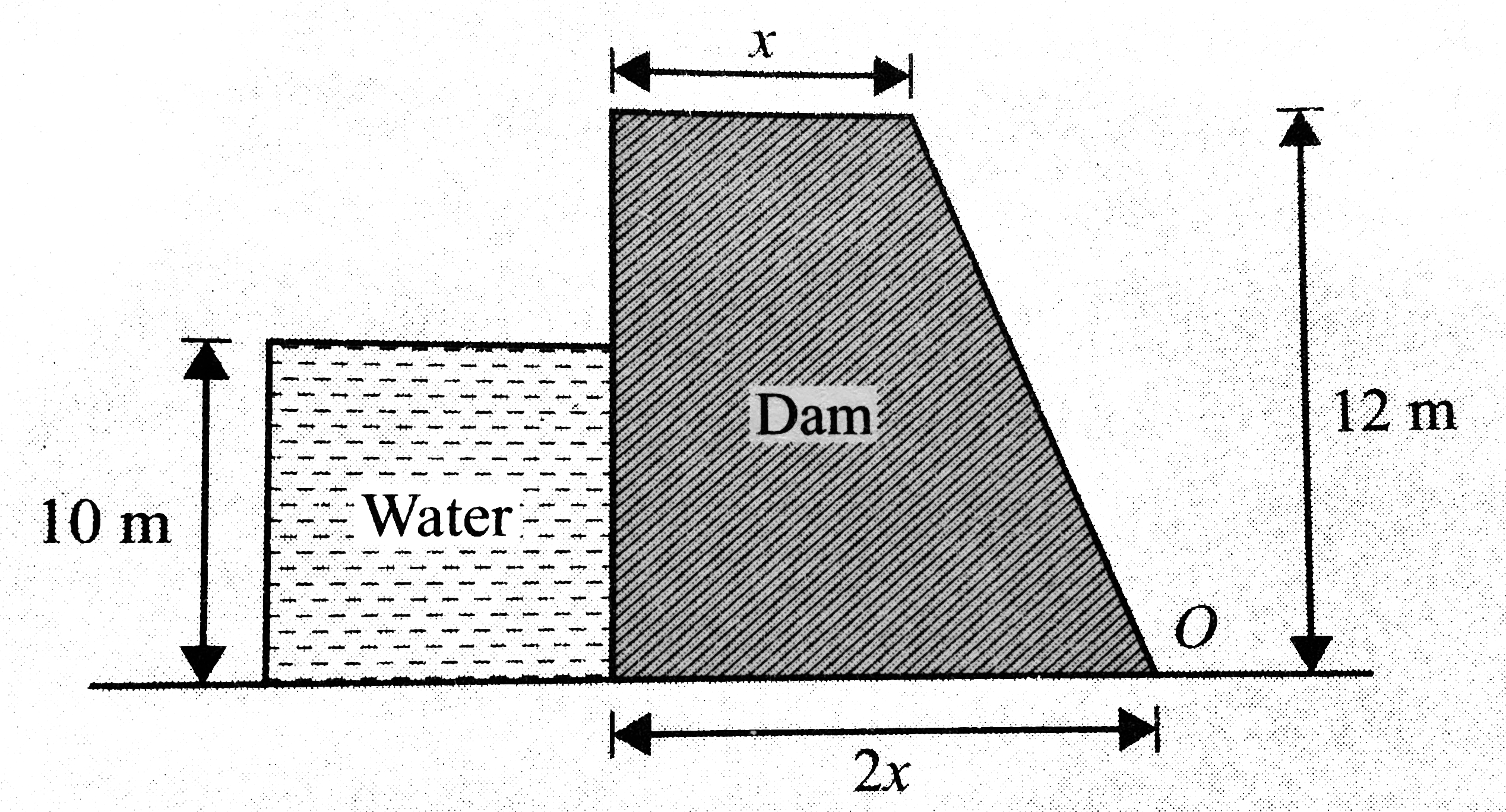
View SolutionFigure shows a cross sectional view of a masonry dam whose length perpendiclar to te diagram is `30 m`. The depth of the water behind te dam is `10 m`. the masonry of which is the dam is constructed has a density of `3000 kg//m^(3)`.
a. Find the dimensions `x` and `2x` if the weight of the dam is to be `10` times the horizontal force exerted on it by water.
b. Check the stability of the dam with respect to its overturning about the edge through point `O`.
View SolutionWater and liquid are filled up behind a square wall of side. Find out
a. pressures at `A, B` and `C`
b. forces in part `AB` and `BC`
c. total force and point of application of force (neglect atmospheric pressure in every calculation)
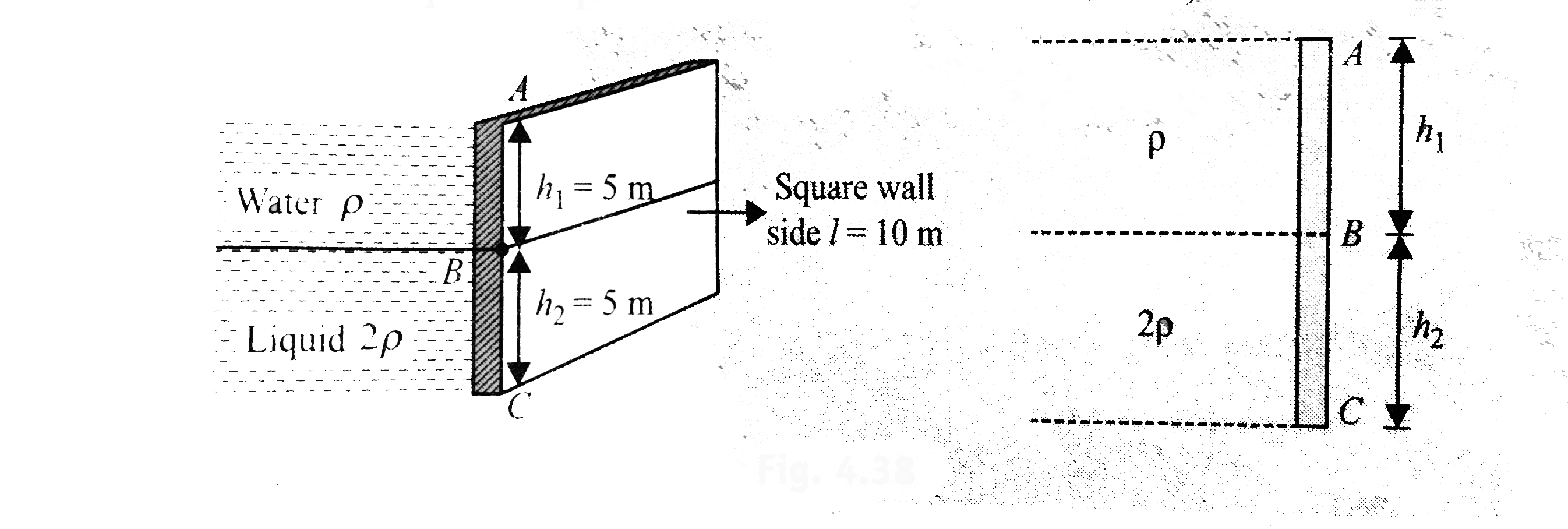
View SolutionFind the net downward thrust on the clined surface of a bucket full of water of height `h` and radii `a` and `b`.
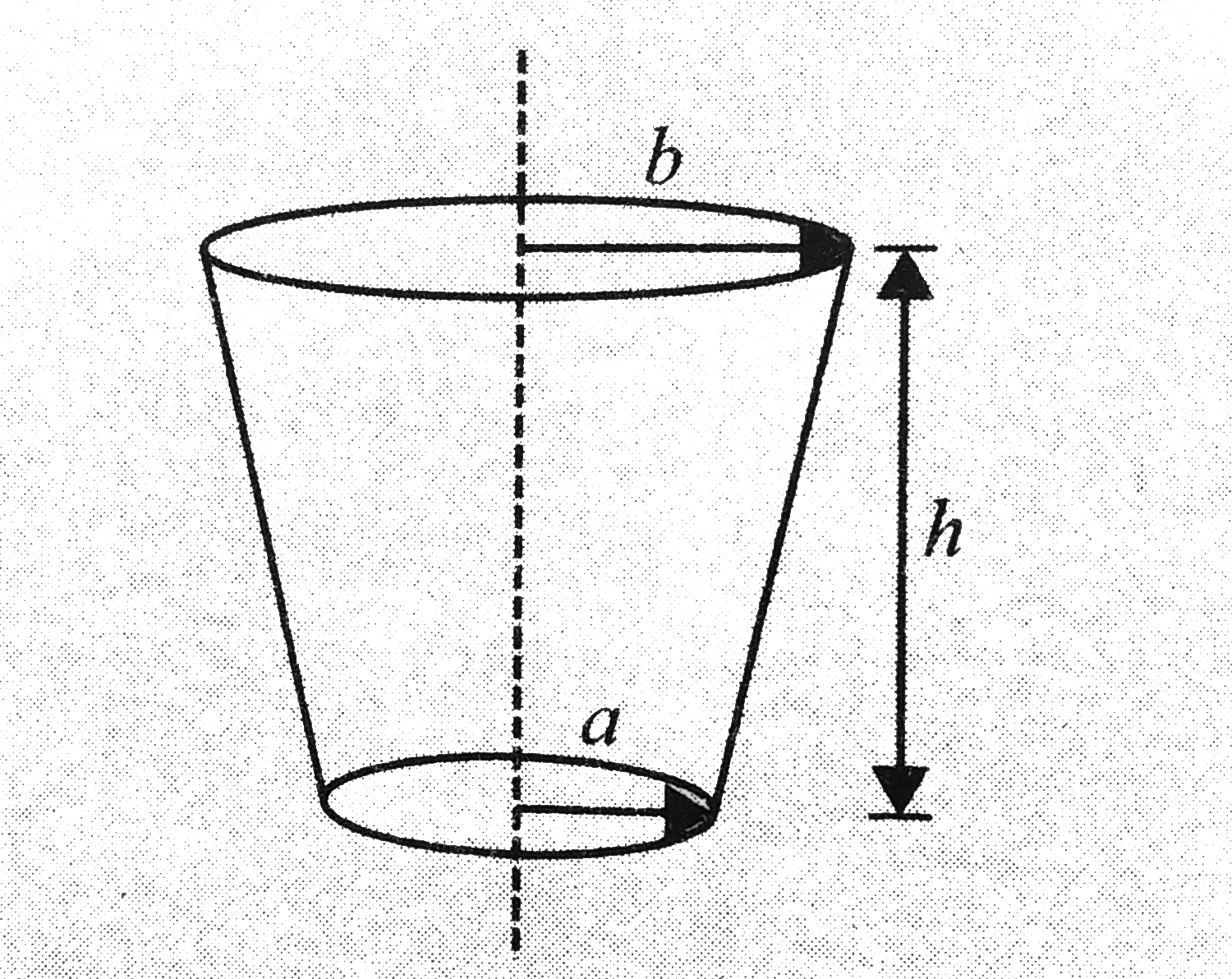
View SolutionWater is retained by a curved gate `AB`. Compute the horizontal and vertical component of the resultant of the hydrostatic pressure dsitribution on the gate `AB`, which is a quarter of a cylinder. Assume that the gate is `4m` wide.

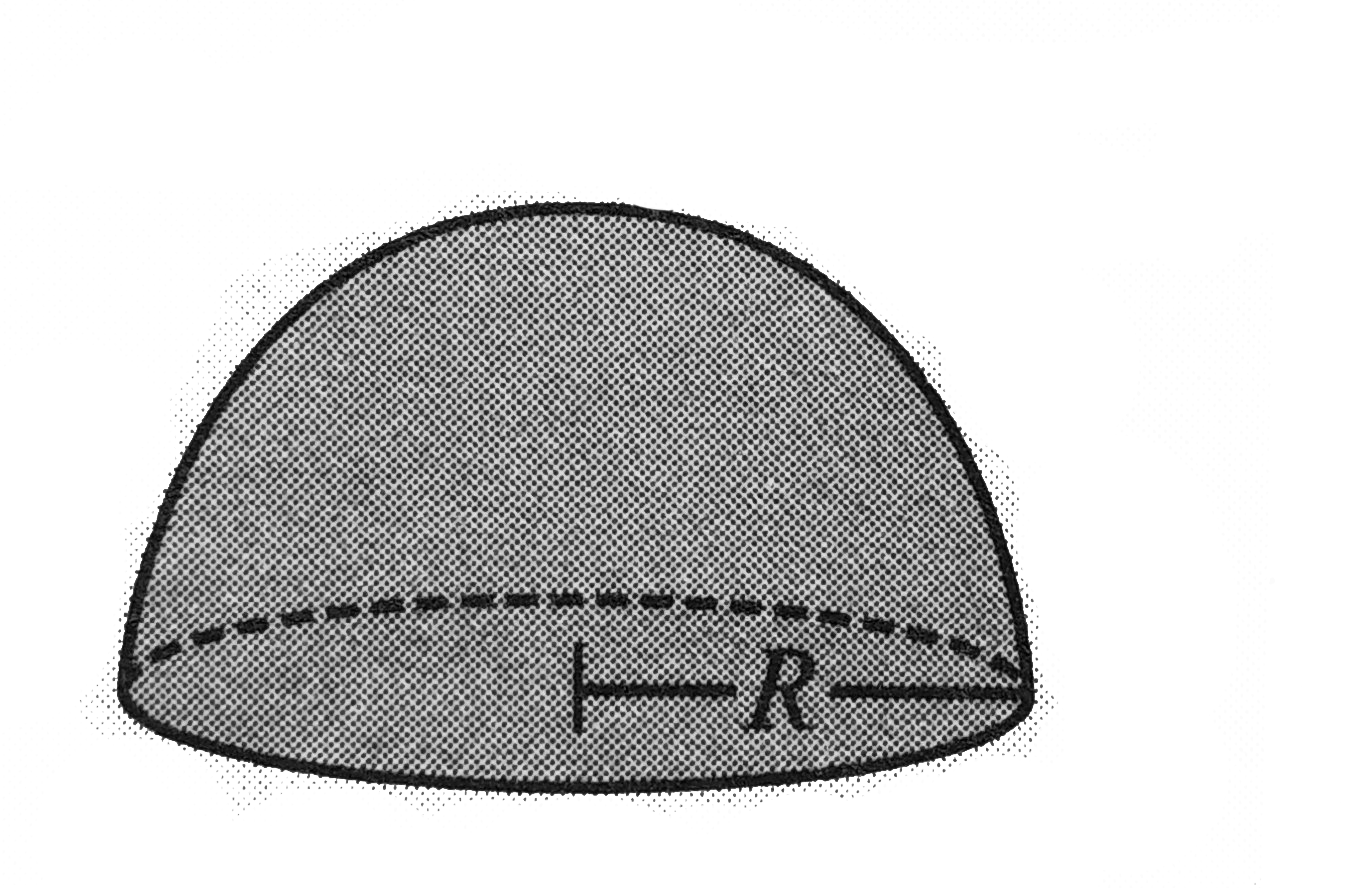
View SolutionA solid hemisphere of radius `R` is made to just sink in a liquid of density `rho`. Find a. the vertical thrust on the curved surface b. the vertical thrust on the flat surface c. the side thrust on the hemisphere. d. the total hydrostatic force acting on the hemisphere.
View SolutionA cylinderical tank of radiuus `20 cm` and height `50 cm` has water up to `30 cm` of height. What will be the rise in level of liquid at the periphery if the cylinder be givenan angular velocity of `10 rad s^(-1)`? Also determine the frequency of rotation when water just starts spilling over the sides of the vessel.
View SolutionA cylindrical vessel of diameter `0.3 m` and height `0.6 m` is filled two thirds with a liquid of specific gravity `0.8`. The vessel is rotated about its axis. a. Determine the speed of rotation when the liquid just starts spilling. b.Find the speed of rotation when the base is just visible. c. What is the percentate of liquid left in the vessel?
View SolutionA `U`-tube rotates with angular velocity `omega` about the vertical axis `AB`. What is the difference in fluid level h in terms of `omega` the radii `r_(1)` and `r_(2)` and the fluid density `rho?`
View SolutionA beaker containing water is placed on the pan of a balance which shows a reading of `M`. A lump of sugar of mass `m` ad volume `v` is now suspend by a thread (from an independent support) in such a way that it is completely immersed in water without touching the beaker and without any overflow of water. How will the reading change as time passes on?
View SolutionA piece of ice of floating in water. What will happen to the level water all ice melts? What will happen if the beaker the filled not with water but with liquid a. denser than water, b. lighter than water?
View SolutionA liquid of density `rho` is filled in a beaker of cross section `S` to a height `H` and then a cylinder of mass `m` and corss section `s` is made to float in it as shown in figure. It the atmospheric pressure is `p_(0)`, find the pressure a at the top face `A` of the cylinder `b` at the botom face `C` of the cylinder and c. at the base `B` of the beaker. Can ever these three pressures be equal?

View SolutionWhat fraction of an iceberg ice beneath the surface of the sea? Density of sea water `(rho)=1.028xx10^(3)kg//m^(3)`, density of ice d. `=0.917xx10^(3)kg//m^(3)`
View SolutionA cubical block of wood `10 cm` along each side floats at the interface between an oil and water with its lowest surface `2cm` below the interface. If the height of oil and water columns are `10 cm` each and `rho_("oil")=0.8g/"cc",` find a the mass of the block, b. the liquid pressure at the lower surface of the block.
View SolutionA cube of wood supporting 200gm mass just floats in water. When the mass is removed, the cube ruses by 2cm. What is the size of the cube?
View SolutionA glass sphere has a cavity inside it. whhen placed in water, it floats with `20` of its volume above the water surface. Find the volume of the cavity as a fraction of total volume (density of glass `=2.5g//"cc")`.
View SolutionA rod of length `6m` has a mass of `12 kg`. It is hinged at one end of the rod at a distance of `3m` below the water surface.
a. What must be the weight of a block that is attached to the other end of the rod so that `5 m` of the rod's length is under water?
b. Find the magnitude and direction of the force exerted by the hinge on the rod. The specific gravity of the material of rod is `0.5.`

View SolutionA vessel contains two immiscible liquids of densit `rho_(1)=1000 kg//m^(3)` and `rho_(2)=1500kg//m^(3)`. A solid block of volume `V=10^(3)m^(3)` and density `d=800kg//m^(3)` is tied to one end of a string and the outer end is tied to the bottom of the vessel as shown in figure.
The block is immersed with two fifths of its volume in the liquid of lower density. The entire system is kept in an elavator which is moving upwards with an acceleration of `a=g/2`. Find the tension in the string. brgt
View SolutionA solid sphere of mass `m=2 kg` and density `rho=500kg//m^(3)` is held stationary relative to a tank filled with water. The tank is acceerating upward with acceleration `2m//s^(2)`. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank. (Density of water`=1000kg//m^(3),g=10m//s^(2))`

View SolutionA pipe of non uniform cross section has two distinct section ` 1` and `2 ` with areas `2cm^(2)` and `4cm^(2)` respectively. If the velocity of flowing liquid at section `1` is `5cm//s`, determine the velocity at section `2`.
View SolutionA broad pipe having a radius `10 cm` branches into two pipes of radii `5 cm` and `3cm`. If the velocity of flowing water in the pipe of radius `3 cm` is `5 cm//s`, determine the velocities of water in the remaining two pipes. Given that the rate of discharge through the main branch is `600picm^(3)//s`.
View SolutionA liquid moves in a smoothh tube of uniform cross section. Find the pressure `P_(2)` at point `2` of the tube if the pressure at point `1` of the extended tube is `P_(1)` and the vertical distance between points `1` and `2` is `h`. brgt

View SolutionA bent tube is lowered into a water stream as shown in figure. The velocity of the stream is `V_(1)`. The closed upper end is located at a height `h_(0) ` and has a small orifice. To what height `h` will the liquid get spurt? brgt

View SolutionA horizontal cylinder of length `l` contains water. On the left a constant force `F` is applied on the piston and on the right there is a small hole of area a. What is the velocity of the piston? Hence, calculate the work done in emptying the vessel in time `t`. brgt
 given area of cylinder is A
given area of cylinder is A
View SolutionA cylindrical vessel of area of cross section `A` is filled with a liquid up to a height `H`. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionA wide vessel with a small hole in the bottom is filled with water and kerosene. Find the velocity of water flow if the thickness of water layer is `h_(1)=30 cm` and that of kerosene is `h_(2)=20cm` brgt

View SolutionOn the opposite sides of a wide vertical vessel filled with water, two identical holes are opened, each having cross sectiona area a. The height dference between them is equal to `h`. Find the resultant force of reaction of water flowing out of vessel.
View SolutionThe side wall of a wide vertical vessel of height `h=75 cm` a narrow slit (vertical) running all the way down to the bottom of the vessel.
The length of the slit is `l=50 cm` and the width is `b=1 mm`. With the slit closed, water is filled to the top. Find the resultant reaction force of water coming out as the slit is opened. brgt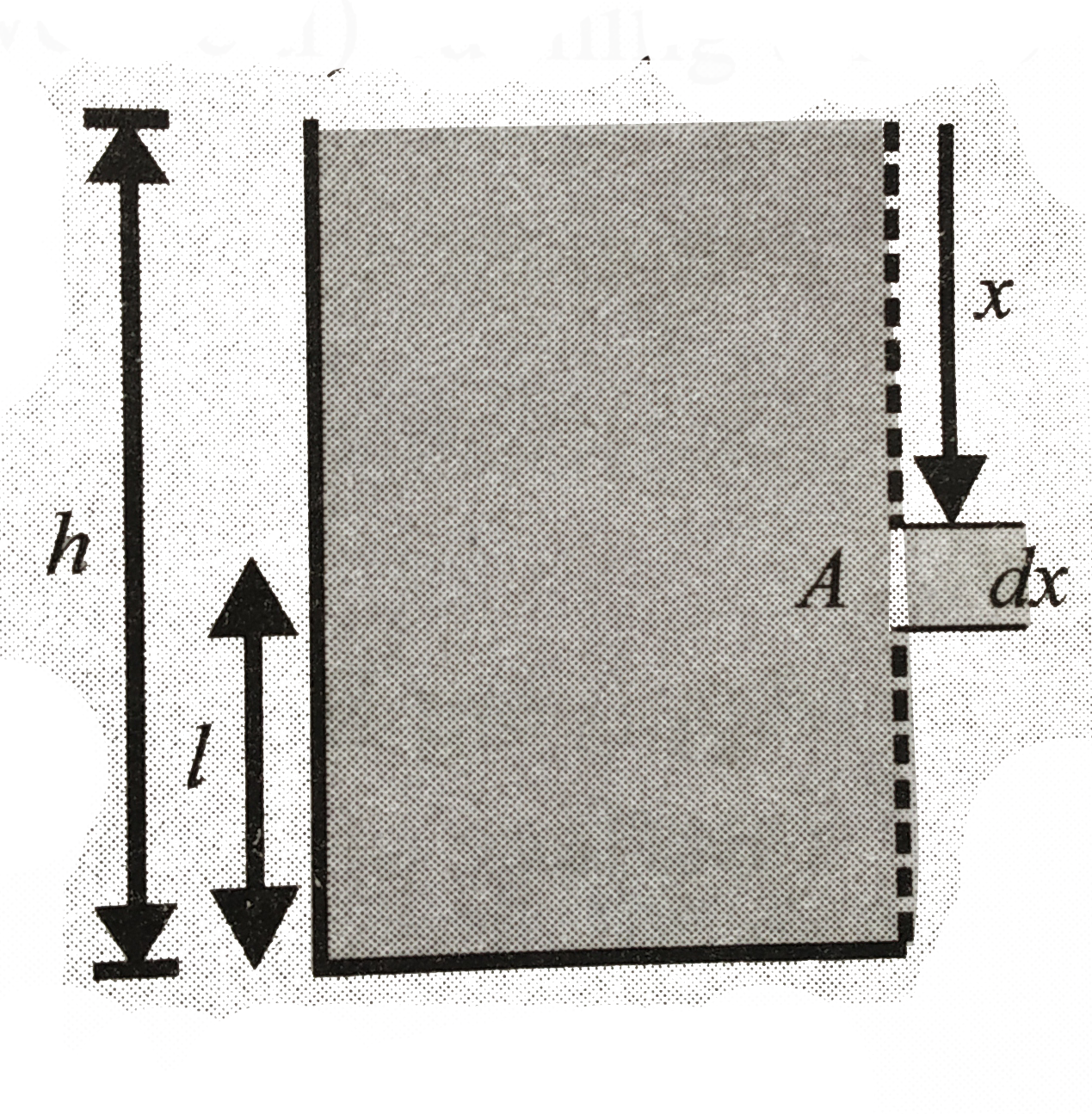
View Solution
Illustration questions and complete solutions for chapter FLUID MECHANICS of CENGAGE PHYSICS (HINGLISH) of Class 11