Complete Solutions to Subjective of chapter KINEMATICS-1 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS-1 |
| CENGAGE PHYSICS | Subjective |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
A car starts from rest and moves with constant acceleration and covera the distance between two point `180 m` apart in `6 s`. Itsspeed as it passes the second point is `45 ms^(-1)` Find
a. Its acceleration
b. Its speed when it was at the point
c. The distance from the first point when it was at rest`.
View SolutionA stone is let to fall from a balloon ascending with an acceleration `f`. Aftre time `t`. A second stonr is dropped. Prove that the distance between the stones after time `t'`
since the second stone is dropped, is `(1)/(2) (f+g)t(t+2t')`.
View SolutionA stone falling from the top of a vertical tower has descended `x` metre when another is dropped from a point `y` metre, below the top. If they fall from rest and from rest andreach the groundtogerher, show that the height of the tower is `(x+y)^(2))/(4x) m`.
View SolutionDivede a plane `10 m` long and `5 m` high into three parts so that a body starting from rest takes equal times to slide down these. Also find the time taken then.
View SolutionThe driver of a car moving at `30 ms(-1)` suddenly sees a truck that is moving in the same direction at `10 ms^(-1)` and is `60 m` head. The maximum deceletation of the car is `5 ms(-2)`.
a. Will the collision occur if the driver's reaction time is zero ? If so. then?
b. If the car driver's reaction time of `0.5 s` included, what is the minimum deceleration required to avoied the collision?.
View SolutionA steel ball is dropped from th roof of a building. `A` man standing in front of a `1-m` high window in the building notes tha the ball takes `0.1 s` to the fall from the top to the boottom of the window. The ball continues to fall and strikes the ground. On striking the ground, the ball gers rebounded with the same speed with which it hits the ground. If the ball reappears at the bottom of the window `2 s` after passing the bottom of the window on the way down, dind the height of the building.
View SolutionA particle is dropped from the top a tower `h` metre high and at the same moment another particle is projected upward from the bottom. They meet the upper one has descended a distance `h//n` . Show that thevelocities of the two when they meet are in the ratio `2`: `(n-2)` and that the initial velocity of the particle projected upis `sqrt((1//2))n gh`.
View SolutionAn elevator whose floor-to-ceiling destance is `2.50 m` starts ascending with a constant acceleration of `1.25 ms^(-2)` On second after the start, a bolt begins falling from the elevator. Calculate:
a. The free fall time of the bolt
b. The displacement and reference frame of ground.
View SolutionTwo motor cars start from A simultaneously & reach B after 2 hour. The first car travelled half the distance at a speed of `v_(1)=30 km hr^(-1)` & the other half at a speed of `v_(2)=60 km hr^(-1)`. The second car covered the entire with a constant acceleration. At what instant of time, were the speeds of both the vehicles same? Will one of them overtake the other enroute?
View SolutionA train of length `l=350m` starts moving rectilinearly with constant acceleration `w=3.0*10^-2 m//s^2`, `t=30s` after the start the locomotive headlight is switched on (event 1), and `tau=60s` after that event the tail signal light is switched on (event 2). Find the distance between these events in the reference frames fixed to be train and to the Earth. How and at what constant velocity V relative to the Earth must a certain reference frame K move for the two events to occur in it at the same point?
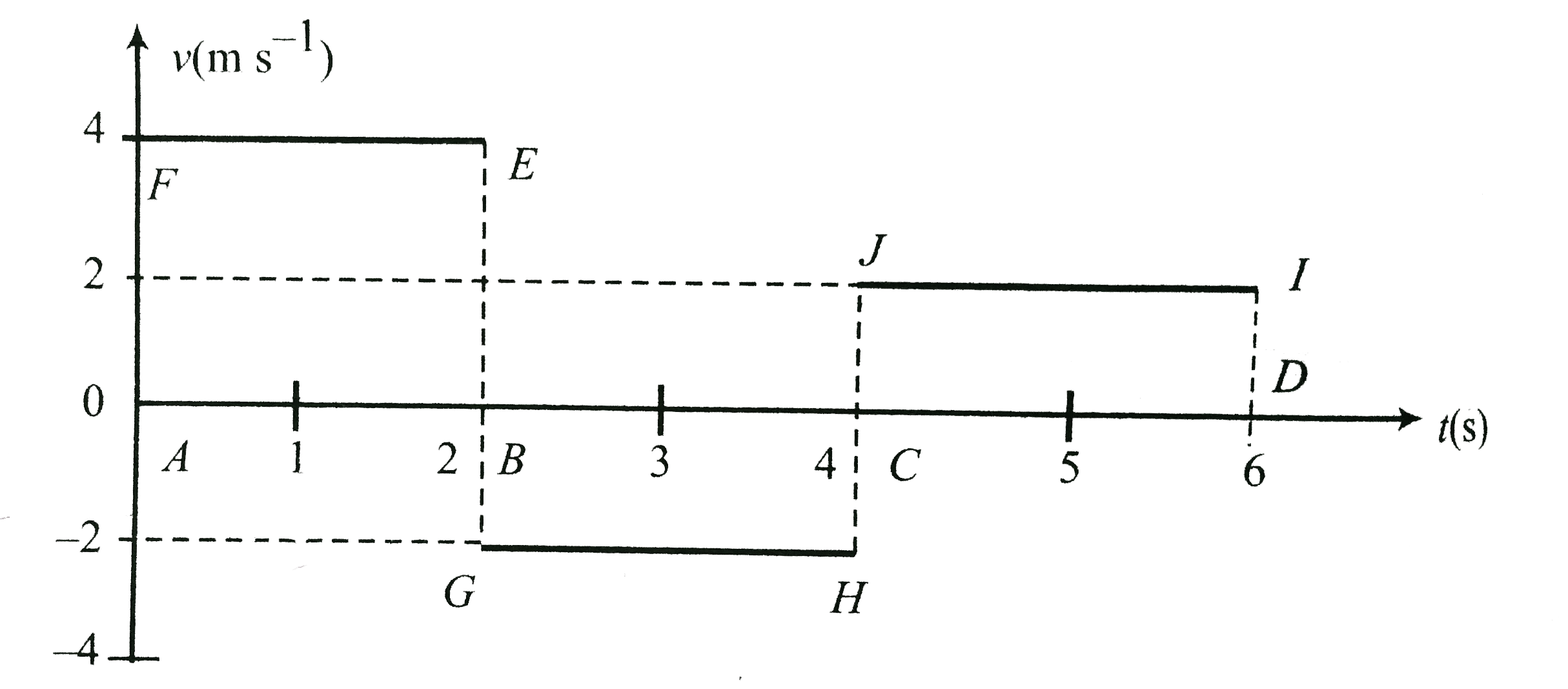
View SolutionStarting at `x=0`, a particle moves according to the graph of `v` vs `t` shown in . Sketch a staph of the instantaneoud acceleration `a` vs `t`, indicationg numerical values at significant points of the graph.
 .
.
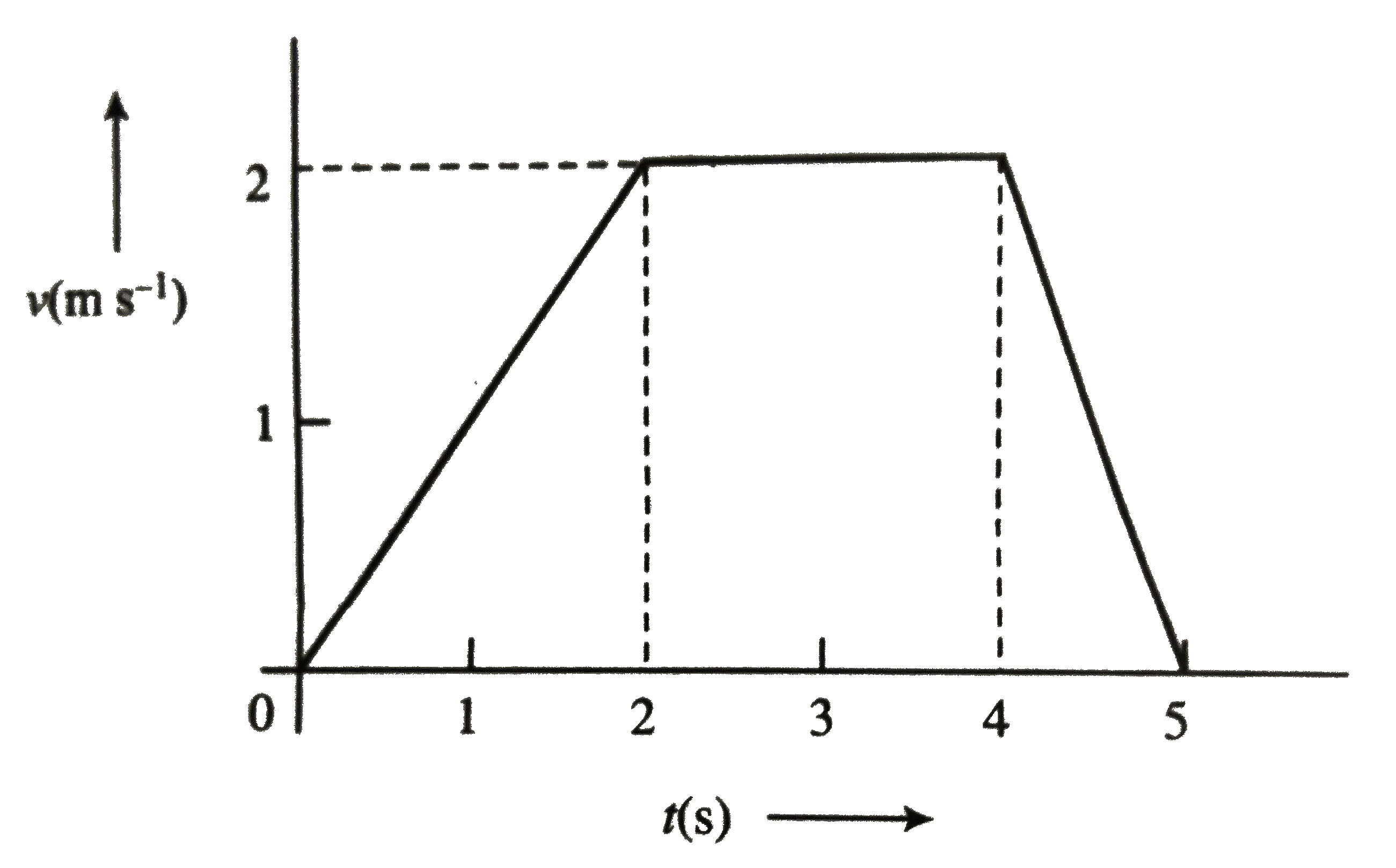
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in `6 s`.
 .
.
View SolutionShows a graph of the acceleration of a model railroad locomotive moving on the x-axis. Graph its velocity and coordinate as functions of time if `x=0` and `v_(x)=0` at `t=0`.
 .
.
View SolutionA woman starts from her home at `9.00` a. m., walks with a speed of `5 km h^(-1)` on straight road up to her office `2.5 km`away, stays at the offiec up to `5.00 p. m.`, and returnshome by anauto with a seed of `25 kmh^(-1)`. Plot the position-time graph of the woman taking home as origin.
View SolutionA runner jogs a along a straight road (in the `+x` direction) for `30 min`, travelling a distance of `6 km`. She then turns around and walks back towards her starting point for `20 min`, travelling `2 km` during this time.
State true/ false:
a. The final displacement of the entire trip is `0.16 km min^(-1)` .
b. Her average speed for the entire is `0.16 km min^(-1)`.
c. The average velocity for the entire trip is `0.4 km min^(-1)`.
d. The runner's average velocity while jogging is `0.4 km min^(-1)`.
e. Her average velocity while walking is `0.1 km min^(-1)`.
View SolutionAt the instant, the traffic light turns green, a car that has been waiting at an intersection starts ahead with a constant acceleration of `3.20 ms^(-2)`, At the some instant, a truck travelling with a constant speed of `20.0 ms^(-1)`, overtakes and passes the car.
a. At what distance from its starting point does the car overtake the truck?
b. Calculate the speed of the car when it overtakes the truck.
c. Sketch an `x-t` graph of themotion of both vehicles.
Take `x-0` at the intersection.
d. Sketch a `v_(x)-t` graph of the motion of both vehicles.
View SolutionThe acceleration of a particle varies with time as shown in .
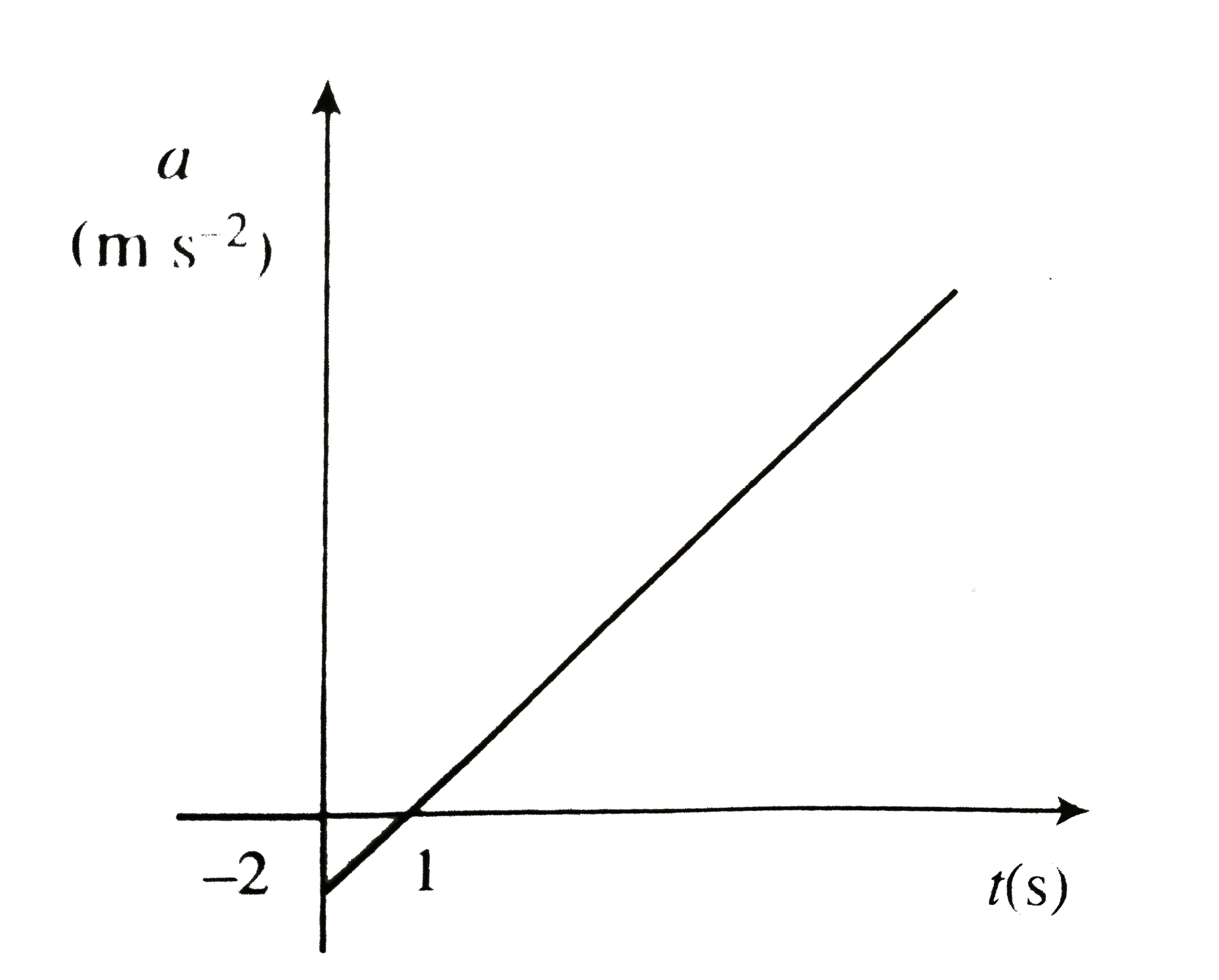 .
.
a. Find an expression for velocityinterms of `t`. Assume that `v=0` at `t=0`
b. Calculate the displacement of the paarticle in the time interval from `t=2s` s.
View SolutionA ball is prouected vertical up from the top of a cliff of height `h` with a speed `v_(1)` Another ball is projected vertically up with a speed `v_(2)` from the bottom of the cliff, after a time `t_(0)` from the instantof projection of the first ball, When will the balls meet?.
View SolutionA body moving along a straight line traversed one third of the total distance with a velocity `4 m//sec` in the first stretch. In the second stretch, the remaining distance is covered with a velocity `2 m//sec` for some time `t_(0)` and with `4 m//s` for the remaining time. If the average velocity is `3 m//sec`, find the time for which body moves with velocity `4 m//sec` in second stretch:
View SolutionA passenger reaches the platform and finds that the second last boggy of the train is passing him. The second last boggy takes `3 s` to pass the passenger, and the last boggy takes `2 s` to pass him. Find the time by which the passnger late for the departure of the trains? Assume that the train accelerates at constant rate and all the boggies are of equal length.
View SolutionReferring to `a-s` diagram as shown in , findthe velocity of the particle when the particle when the spaarticle justcovers `20 m`, `(v_(0)=sqrt50 ms^(-1)`.
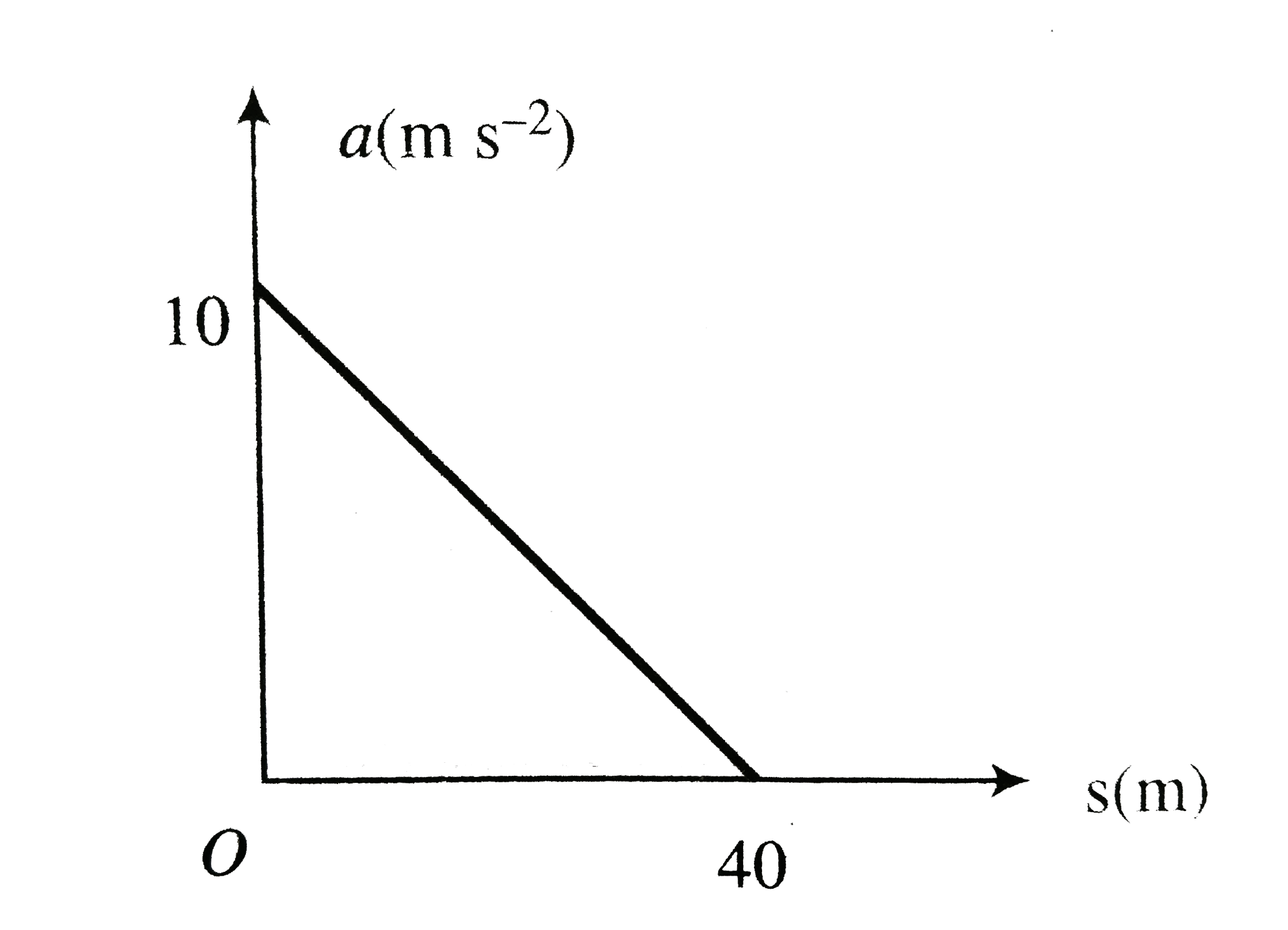 .
.
View SolutionA ballon starts risintg from ground from rest at some constant acceleration. After some time, a storne is dropped from it. If the stone reaches the ground in the same time in which balloon reached the dropping poing from ground, find the acceleration of the balloon.
View SolutionThe balls are released from the top of a tower of heigh `H` at regular interval of time. When first ball reaches at the grund, the nthe ball is to be just released and `((n+1))/(2) th`
ball is at some distance `h` from top of the tower. Find the value of `h`.
View SolutionA car moves in a straight line, the car accelerates from rest with a constant acceleraation `alpha` on a straight foad. After gaining a velocity `v`, the car moves with that velocity for somerime. Then car decelerates with a retardation `beta`, If the total distance covered by the car is equal to `s` find the total time of its motion.
View SolutionA ball is released from the top of a multistory tower. The ball taked ` 1 s` to fall pasta floor of the tower `8 m` height of a floor some distance from the top of thetower. Find the velocities of the ball at the top and at the bottom of the window.
View SolutionA particle is projected vertically from the ground takes time `t_(1)=1 s` upto point `A`, `t_(2)=3 s` from point `A` to `B`, and time `t_(3)=4 s` from point `B` to highest point. Find the height of the middle point of `A` and `B` from the ground.
View SolutionThe loaded bucket of a craneachievers a maximum velocity `5 m//s` in some time at a uniform rate and thentakes half of this time to stop at a uniform rate after the application of brake. The time differnce between the instants when half of the maximum velocity is achieved is `t (sec)`. Find the displacement of the bucket.
View SolutionAt the same instant, ball `A` is ball `B` is projected vertically building of height `h` and ball `B` is projected vertically upward from the ground with velocity `u`. The ration of velocty of `A` to the velocity of `B` at the point of cllistion is same asthe ratio of height of this point from top of the building to the height from the ground, find the height of the point of collision above theground.
View SolutionA railway track runs parallel to a road until a turn brings the road to railway corssing. A cyclist rides along the road every day at a constant speed `20 km//hr`. He normally meets a train that travels in same direction at the crossing. One day he was late by `25` minutes and met the train `10 km` before the railway crossing. Find the speed of the train.
View Solution
Subjective questions and complete solutions for chapter KINEMATICS-1 of CENGAGE PHYSICS (HINGLISH) of Class 11