Complete Solutions to Linked Comprehension Type of chapter MISCELLANEOUS KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MISCELLANEOUS KINEMATICS |
| CENGAGE PHYSICS | Linked Comprehension Type |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
An inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed `v_0`. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
Just as the student starts his free fall, he presses the button of the stopwatch. When he reaches at the top of 100th floor, he has observed the reading of stopwatch as 00:00:06:00 `(hh:mm:ss:100 th part of the second). Find the value of g. (correct upt ot two decimal places).15:54View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed `v_0`. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
What should be the initial downward speed of the rocketeer so that he catches the student at the top of 100 the floor for safe landing ?15:54View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed `v_0`. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
The position - time graph for rocketeer would be (take the top of building as origin, and vertical downward direction as positive y-axis.)15:54View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed `v_0`. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
In Q.1, what would be the approximate retardation to be given by jet pack along for safe landing?15:54View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed `v_0`. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
The correct velocity - time graph for the rocketeer would be15:54View SolutionAn elevator without a ceiling is ascending up with an acceleration of `5 ms^-2.` A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of `10 ms^-1` and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is `15 ms^-1` with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (`g=10 ms^-2`)
1. The time in which the ball strikes the floor of elevator is given by04:25View SolutionAn elevator without a ceiling is ascending up with an acceleration of `5 ms^-2.` A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of `10 ms^-1` and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is `15 ms^-1` with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (`g=10 ms^-2`)
2. The maximum height reached by ball, as measured from the ground would be06:18View SolutionAn elevator without a ceiling is ascending up with an acceleration of `5 ms^-2.` A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of `10 ms^-1` and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is `15 ms^-1` with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (`g=10 ms^-2`)
3. Displacement of ball with respect to ground during its night would be04:36View SolutionAn elevator without a ceiling is ascending up with an acceleration of `5 ms^-2.` A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of `10 ms^-1` and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is `15 ms^-1` with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (`g=10 ms^-2`)
3. Displacement of ball with respect to ground during its night would be04:36View SolutionAn elevator without a ceiling is ascending up with an acceleration of `5 ms^-2.` A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of `10 ms^-1` and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is `15 ms^-1` with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (`g=10 ms^-2`)
4. The maximum separation between the floor of elevator and the ball during its flight would be06:46View SolutionProjectile motion is a combination of two one-dimensional motion: one in horizontal and other in vertical direction. Motion in 2D means in a plane. Necessary condition for 2D motion is that the velocity vector is coplanar to the acceleration vector. In case of projectile motion, the angle between velocity and acceleration will be `0^@ltthetalt180^@`. During the projectile motion, the horizontal component of velocity ramains unchanged but the vertical component of velocity is time dependent. Now answer the following questions:
A particle is projected from the origin in the x-y plane. The acceleration of particle in negative y-direction is `alpha`. If equation of path of the particle is `y = ax - bx^2`, then initial velocity of the particle is10:13View SolutionProjectile motion is a combination of two one-dimensional motion: one in horizontal and other in vertical direction. Motion in 2D means in a plane. Necessary condition for 2D motion is that the velocity vector is coplanar to the acceleration vector. In case of projectile motion, the angle between velocity and acceleration will be `0^@`lt`theta`lt`180^@`. During the projectile motion, the horizontal component of velocity ramains unchanged but the vertical component of velocity is time dependent. Now answer the following questions:
An object is projected from origin in x-y plane in which velocity changes according to relation `vecv = a hati + bx hatj`. Path of particle is10:13View SolutionProjectile motion is a combination of two one-dimensional motion: one in horizontal and other in vertical direction. Motion in 2D means in a plane. Necessary condition for 2D motion is that the velocity vector is coplanar to the acceleration vector. In case of projectile motion, the angle between velocity and acceleration will be `0^@ltthetalt180^@`. During the projectile motion, the horizontal component of velocity ramains unchanged but the vertical component of velocity is time dependent. Now answer the following questions:
A body is projected at angle of `30^@` and `60^@` with the same velocity. Their horizontal ranges are `R_1` and `R_2` and maximum heights are `H_1 and H_2`, respectively, then
A body is projected at angle of `30^@` and `60^@` with the same velocity. Their horizontal ranges are `R_1` and `R_2` and maximum heights are `H_1` and `H_2`, respectively, then10:13View SolutionA helicopter is flying at `200 m` and flying at `25 ms^(-1)` at an angle `37^@` above the horizontal when a package is dropped from it.
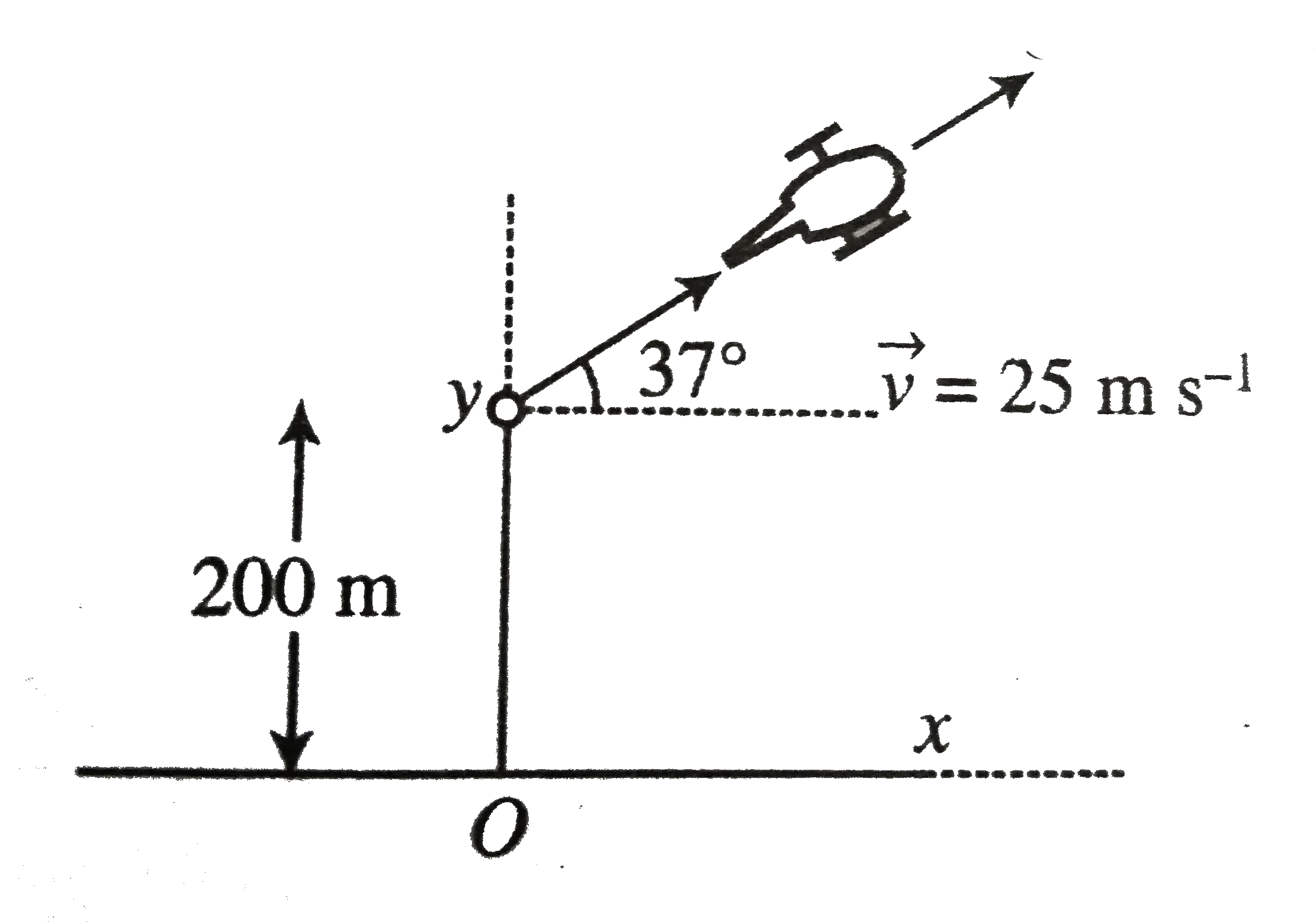
The distance of the point O where the package lands is03:30View SolutionA helicopter is flying at `200 m` and flying at `25 ms^(-1)` at an angle `37^@` above the horizontal when a package is dropped from it.
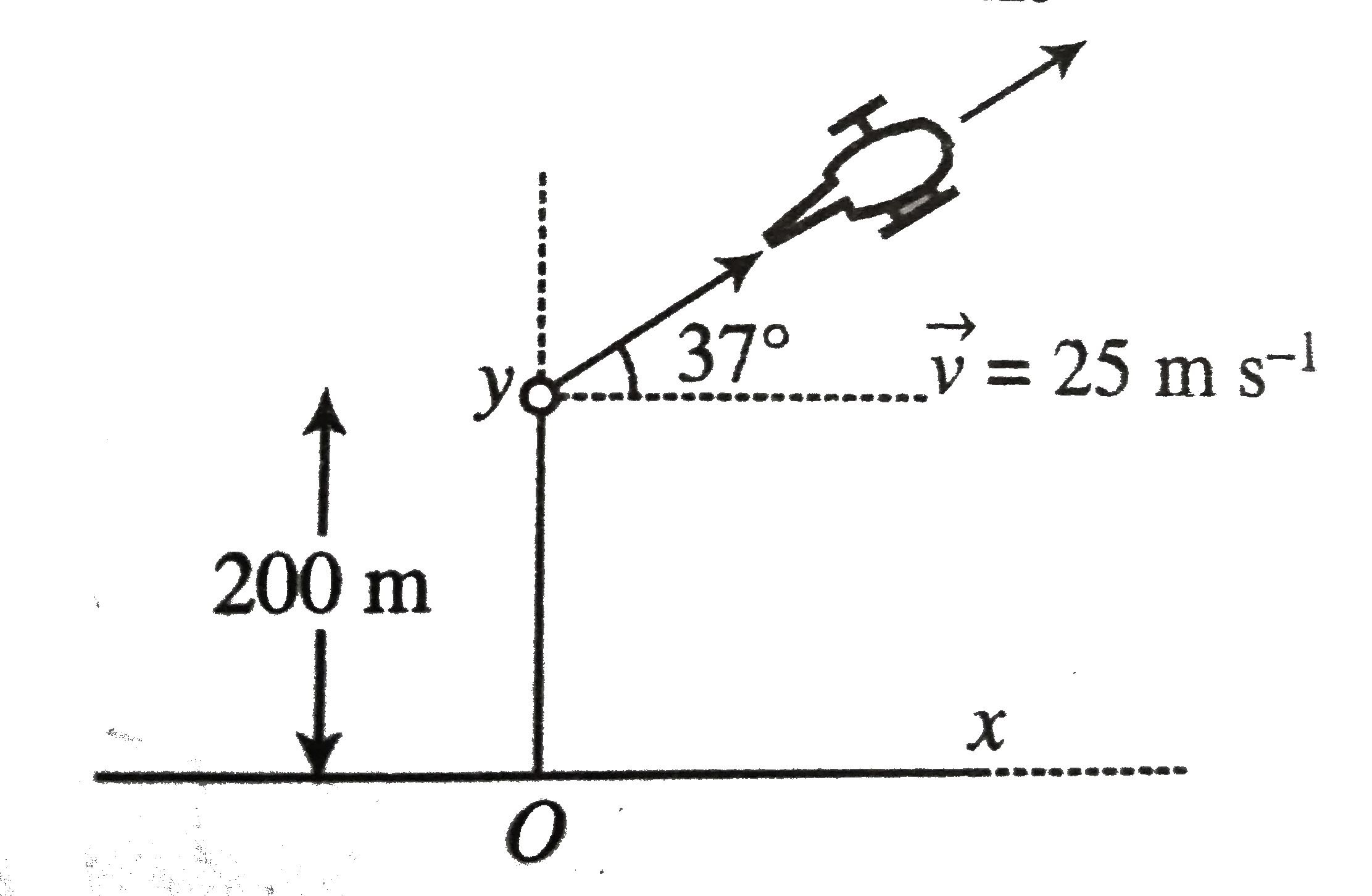
If the helicopter flies at constant velocity, find the x and y coordinates of the location of the helicopter when the package lands.03:30View SolutionTwo particles are thrown simultaneously from points A and B with velocities `u_1 = 2ms^(-1) and u_2 - 14 ms^(-1)`, respectively, as shown in figure.
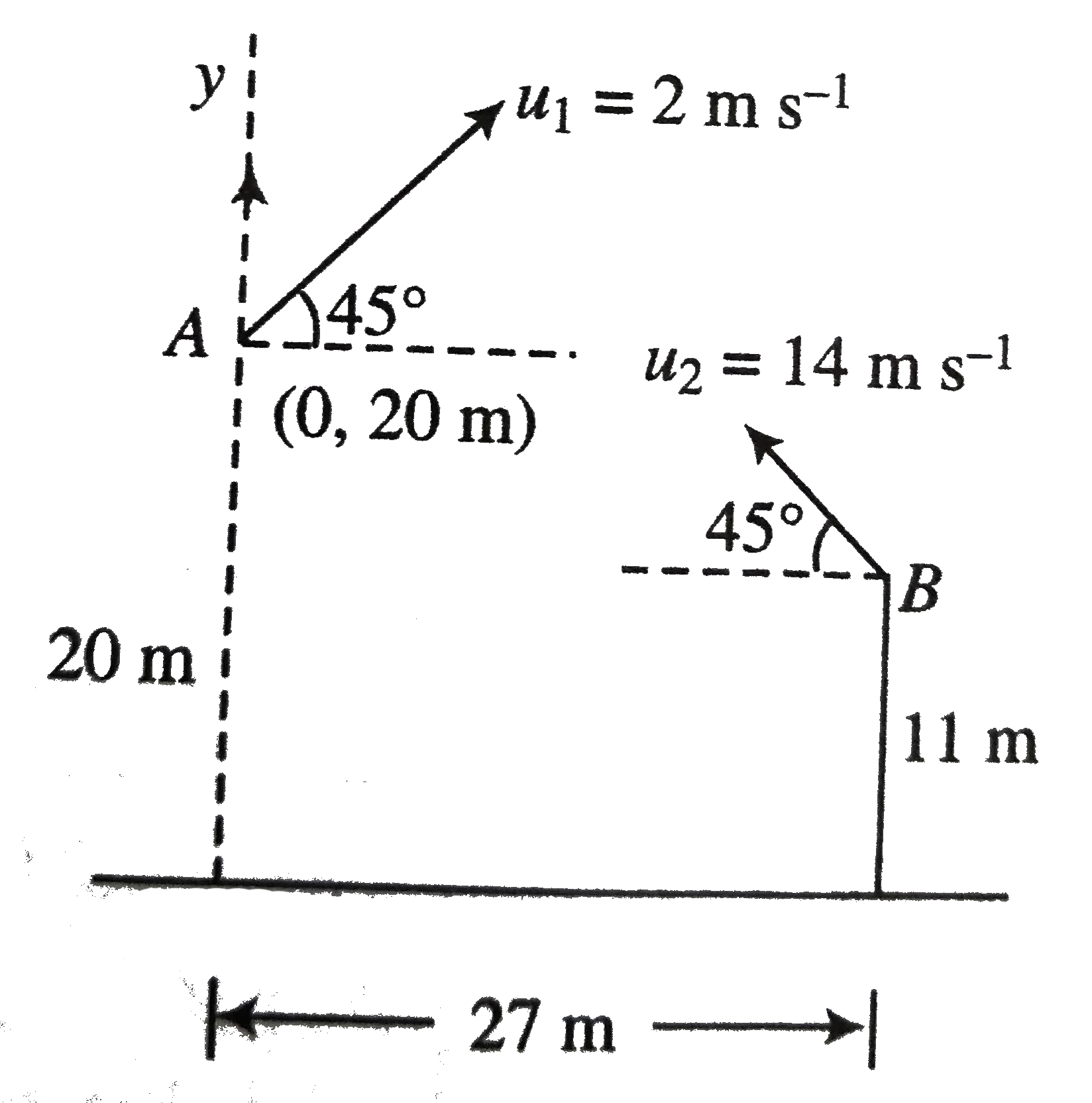
The relative velocity of B as seen from A in05:40View SolutionTwo particles are thrown simultaneously from points A and B with velocities `u_1 = 2ms^(-1) and u_2 - 14 ms^(-1)`, respectively, as shown in figure.
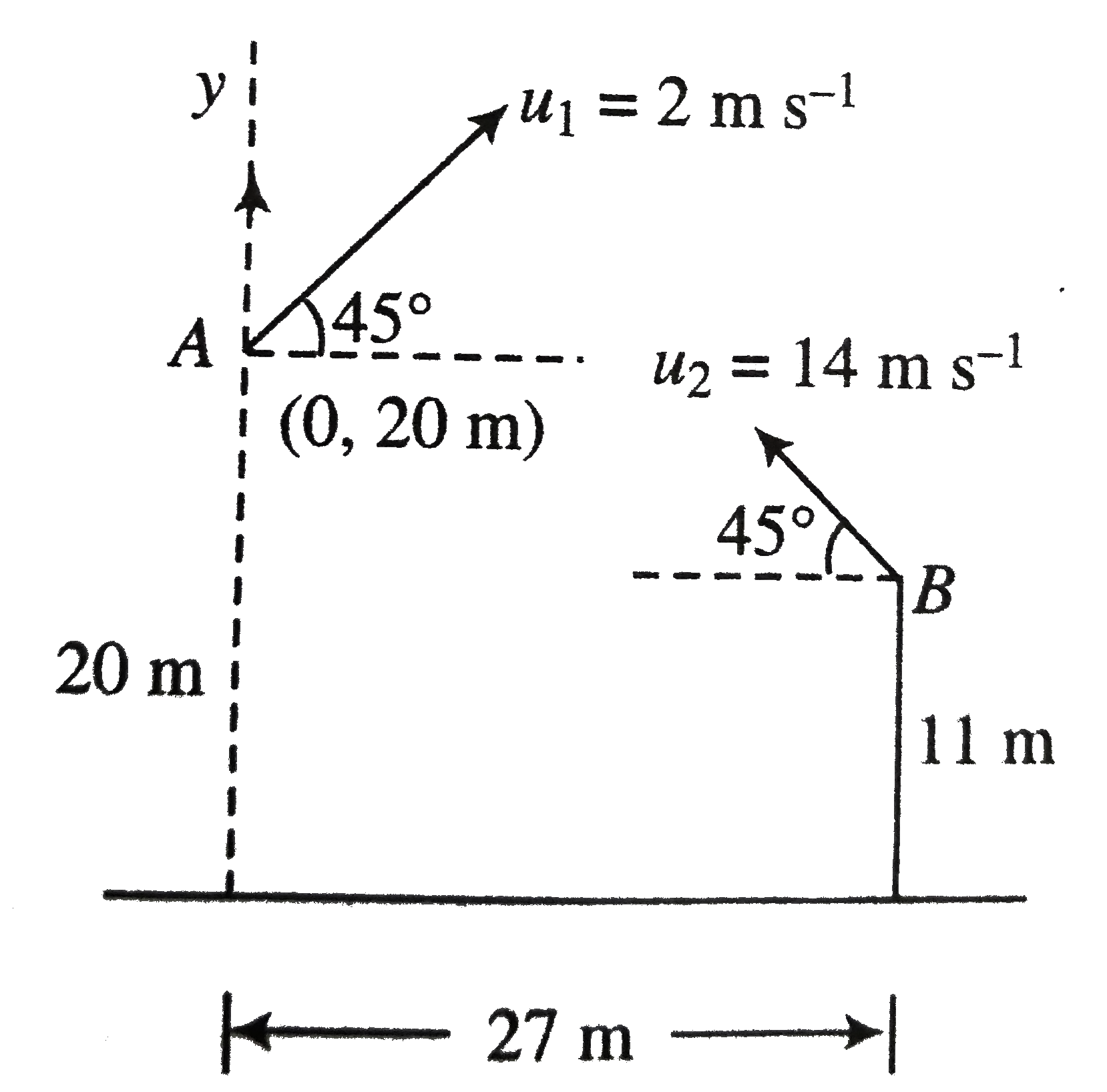
The direction (angle) with horizontal at which B will appear to move as seen from A is05:40View SolutionTwo particles are thrown simultaneously from points A and B with velocities `u_1 = 2ms^(-1) and u_2 - 14 ms^(-1)`, respectively, as shown in figure.
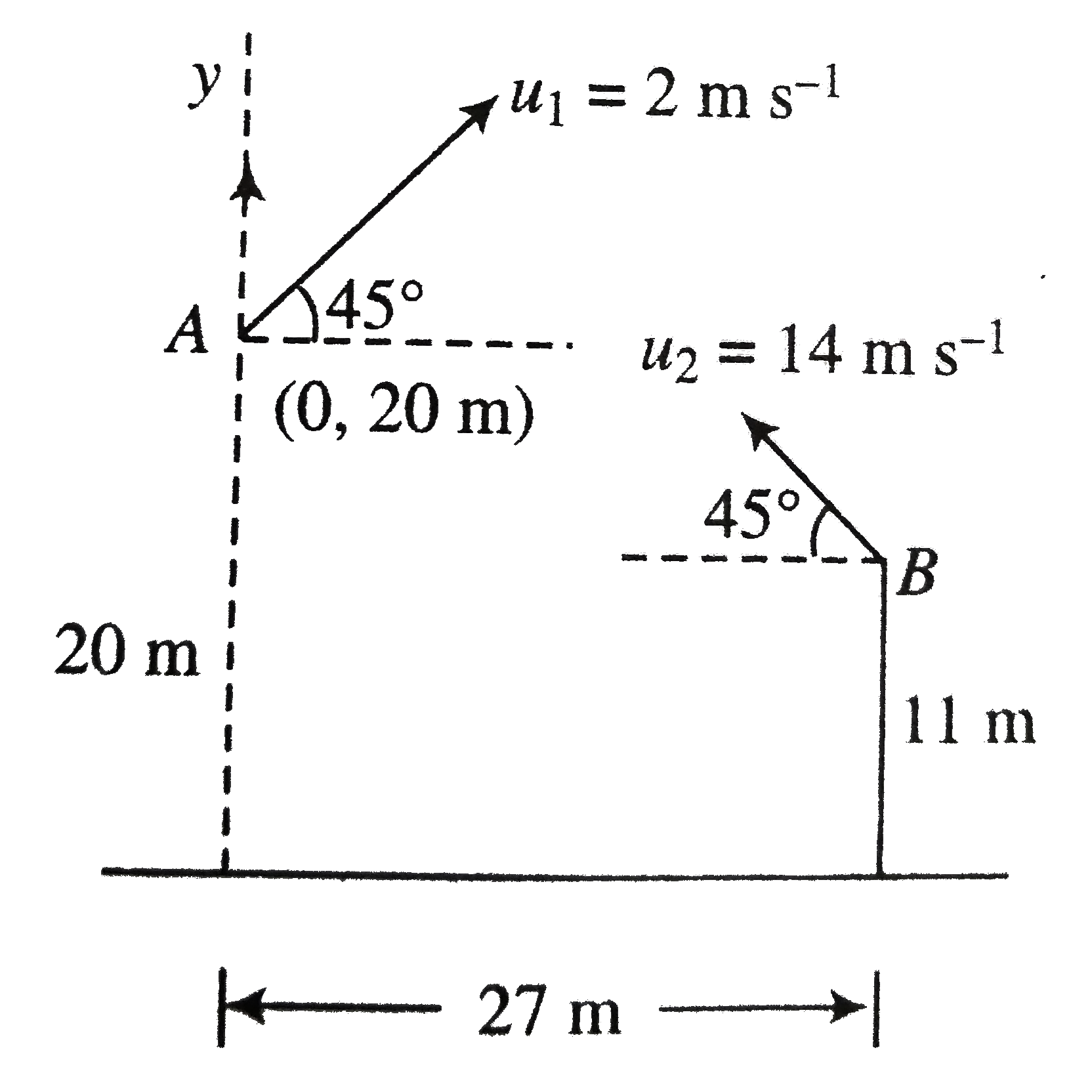
Minimum separation between A and B is05:40View SolutionTwo inclined planes OA and OB having inclination (with horizontal) `30^(@)` and `60^(@)`, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity `u = 10(sqrt3) ms^(-1)` along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate

The velocity with which particle strikes the plane OB,12:12View SolutionTwo inclined planes OA and OB having inclination (with horizontal) `30^(@)` and `60^(@)`, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity `u = 10(sqrt3) ms^(-1)` along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
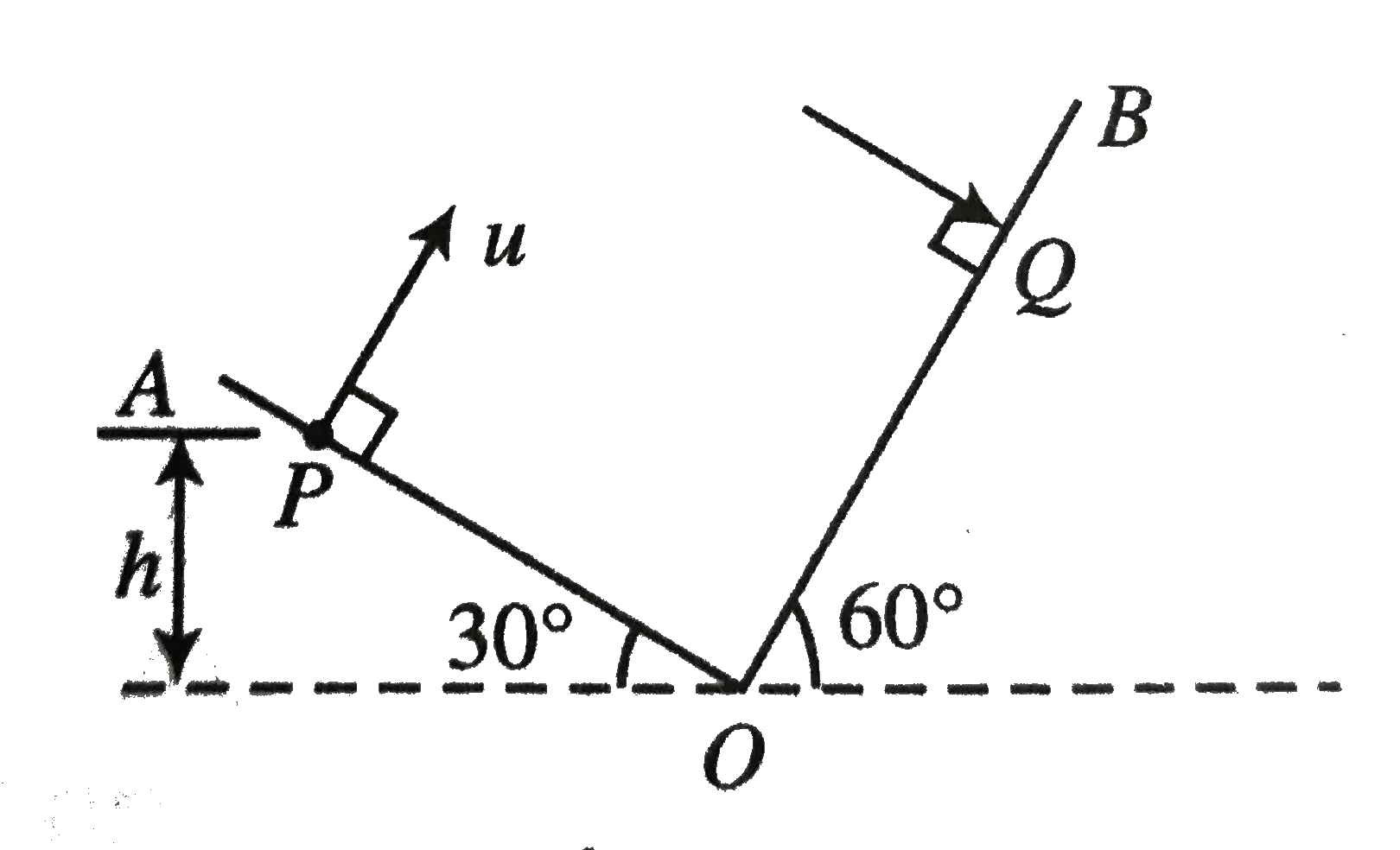
Time of flight of the particles12:12View SolutionTwo inclined planes OA and OB having inclination (with horizontal) `30^(@) and 60^(@)`, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity `u = 10sqrt3 ms^(-1)` along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
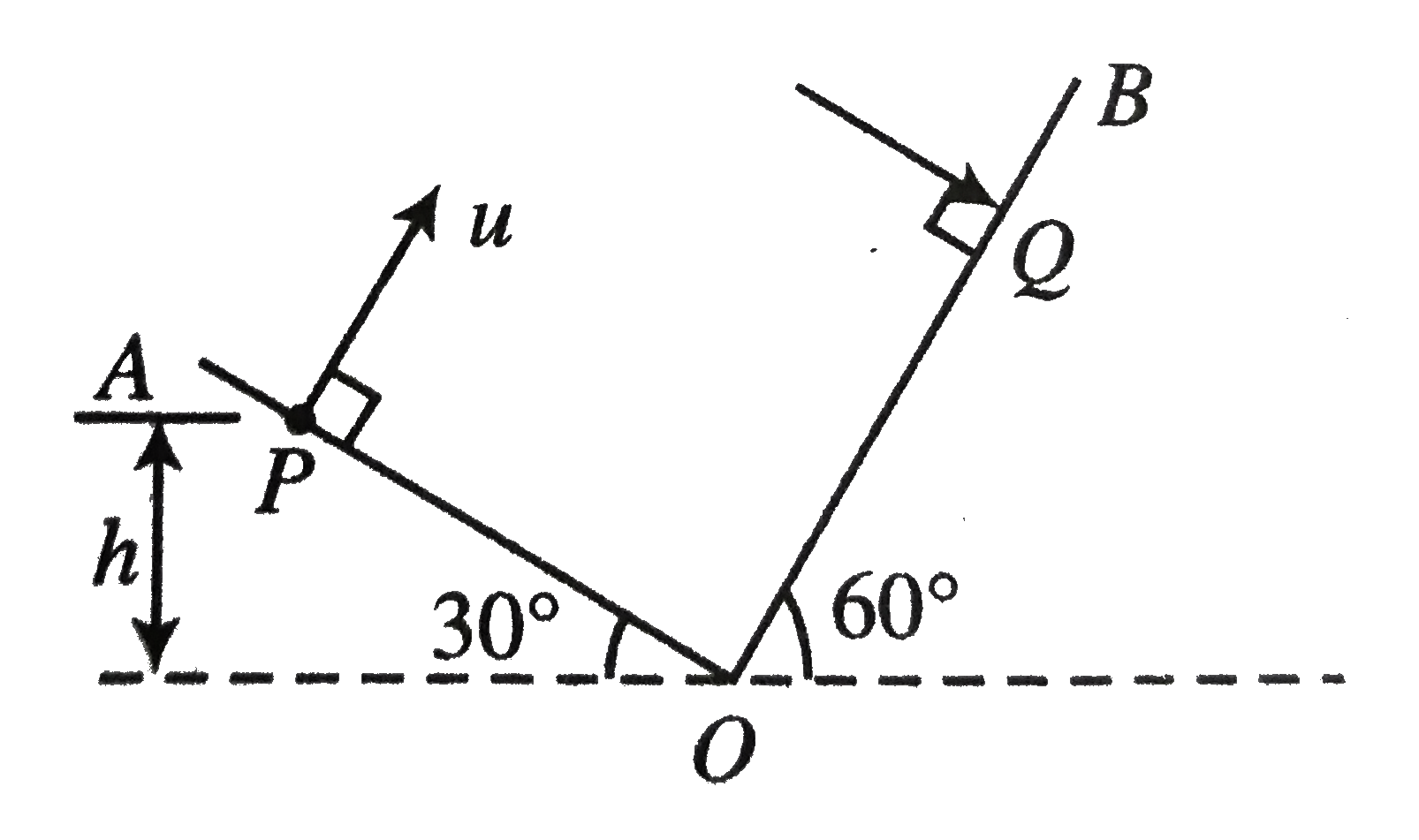
The vertical height h of P from O,12:12View SolutionTwo inclined planes OA and OB having inclination (with horizontal) `30^(@)` and `60^@()`, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity `u = 10sqrt3 ms^(-1)` along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
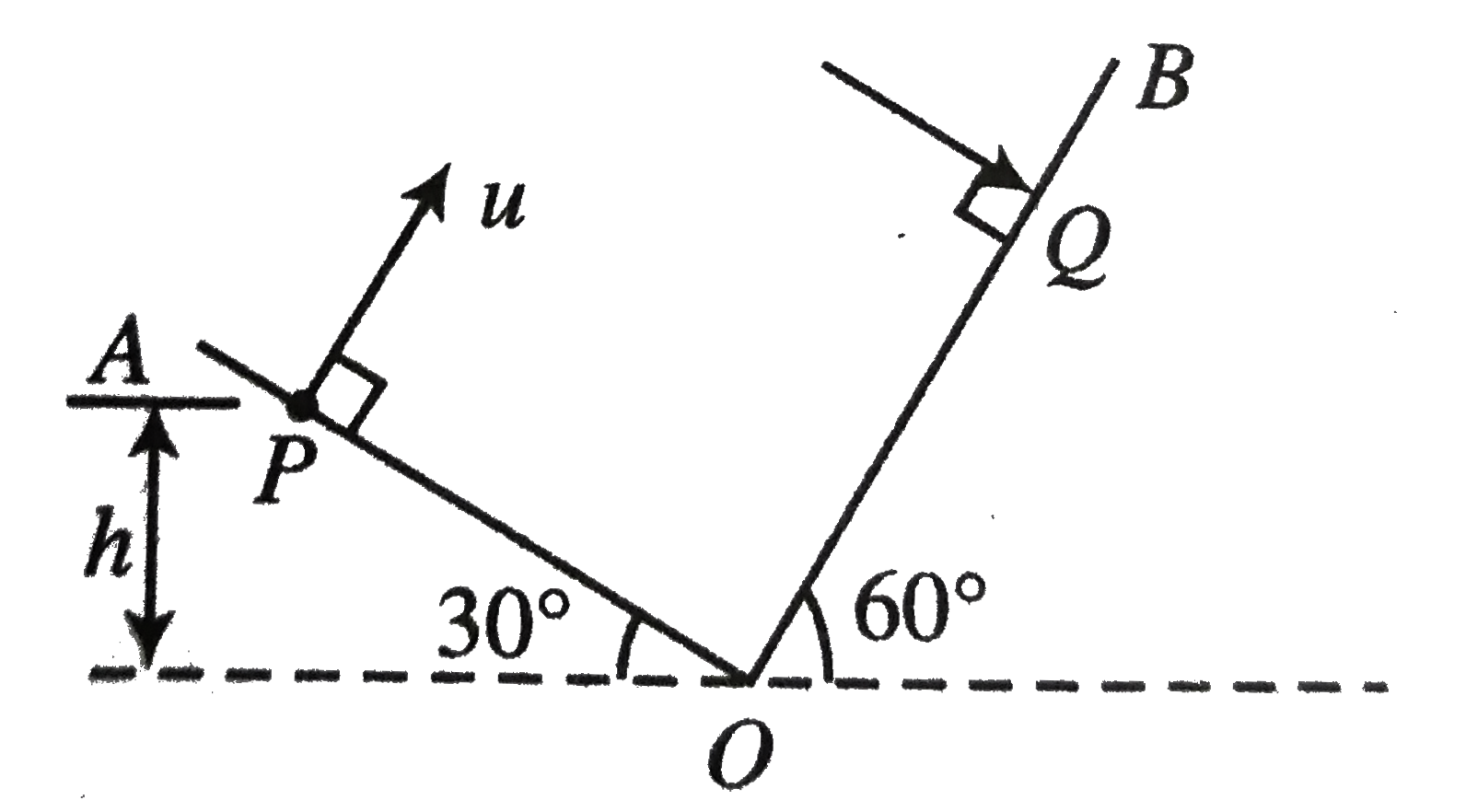
The maximum height attained by the particle (from the line O)12:12View SolutionTwo inclined planes OA and OB having inclination (with horizontal) `30^@` and `60^(@)`, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity `u = 10(sqrt3) ms^(-1)` along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
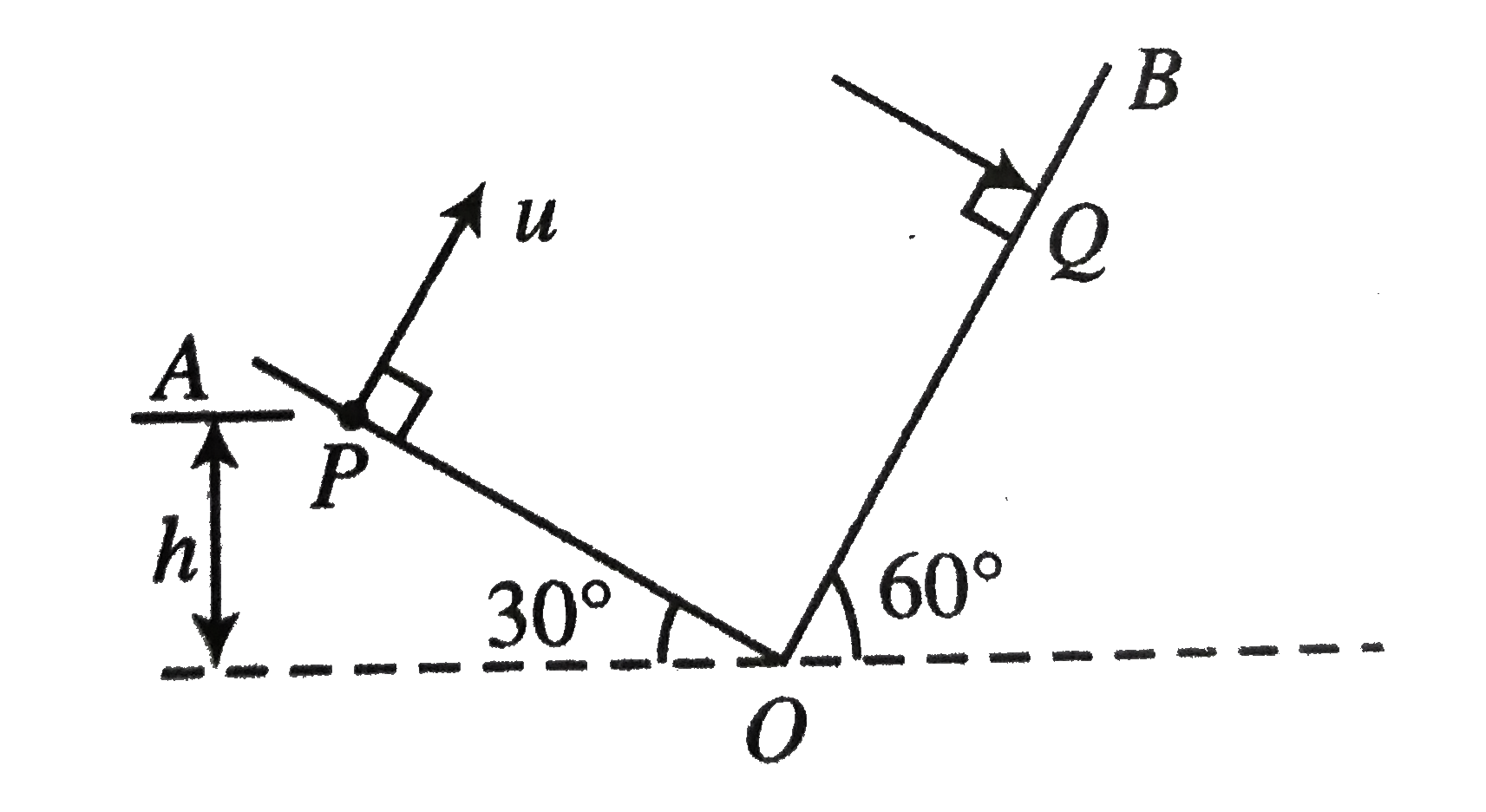
The distance PQ,12:12View SolutionThe x-t graph of a particle moving along a straight line is shown in figure
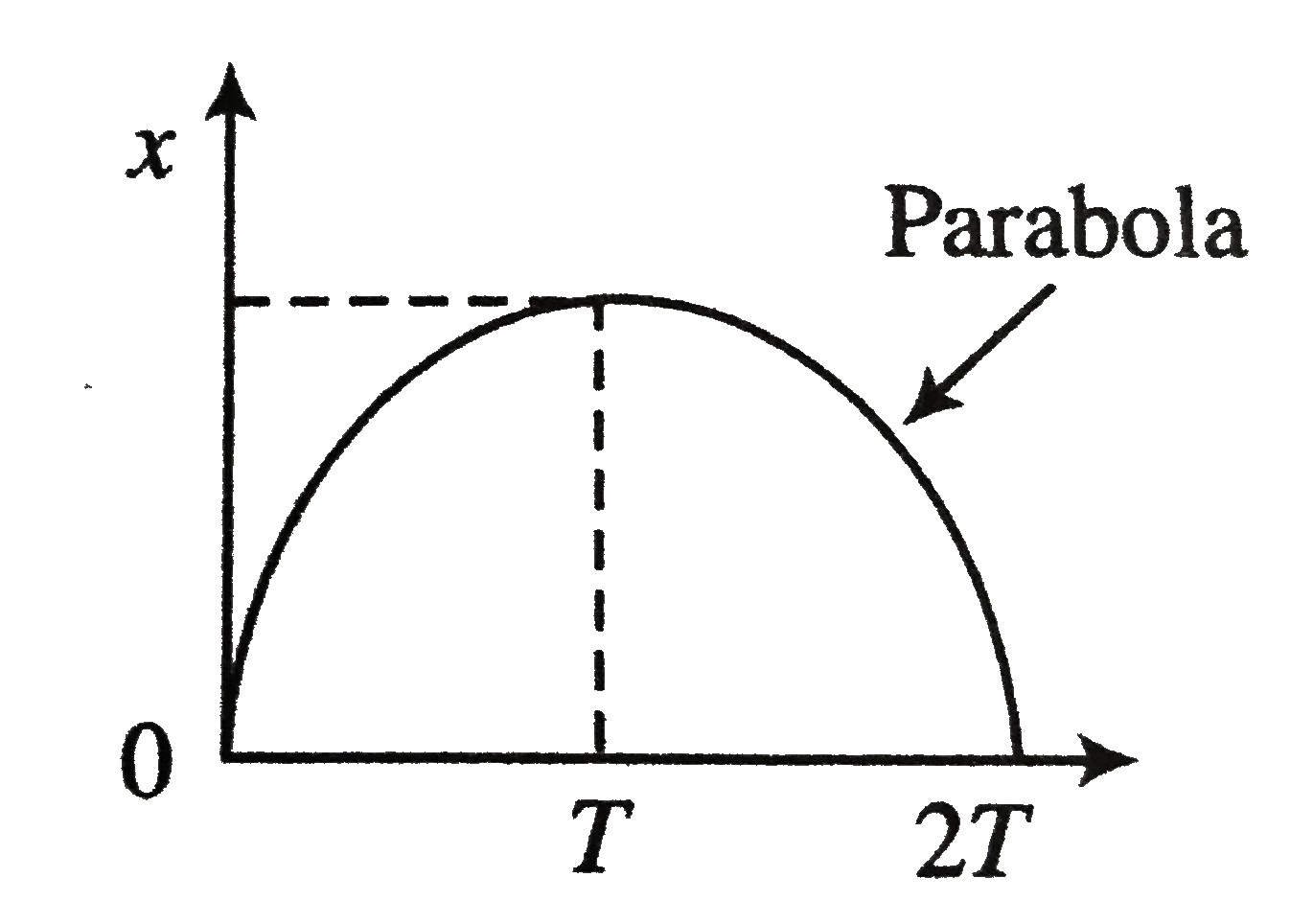
The v-t graph of the particle is correctly shown by06:08View SolutionThe x-t graph of a particle moving along a straight line is shown in figure
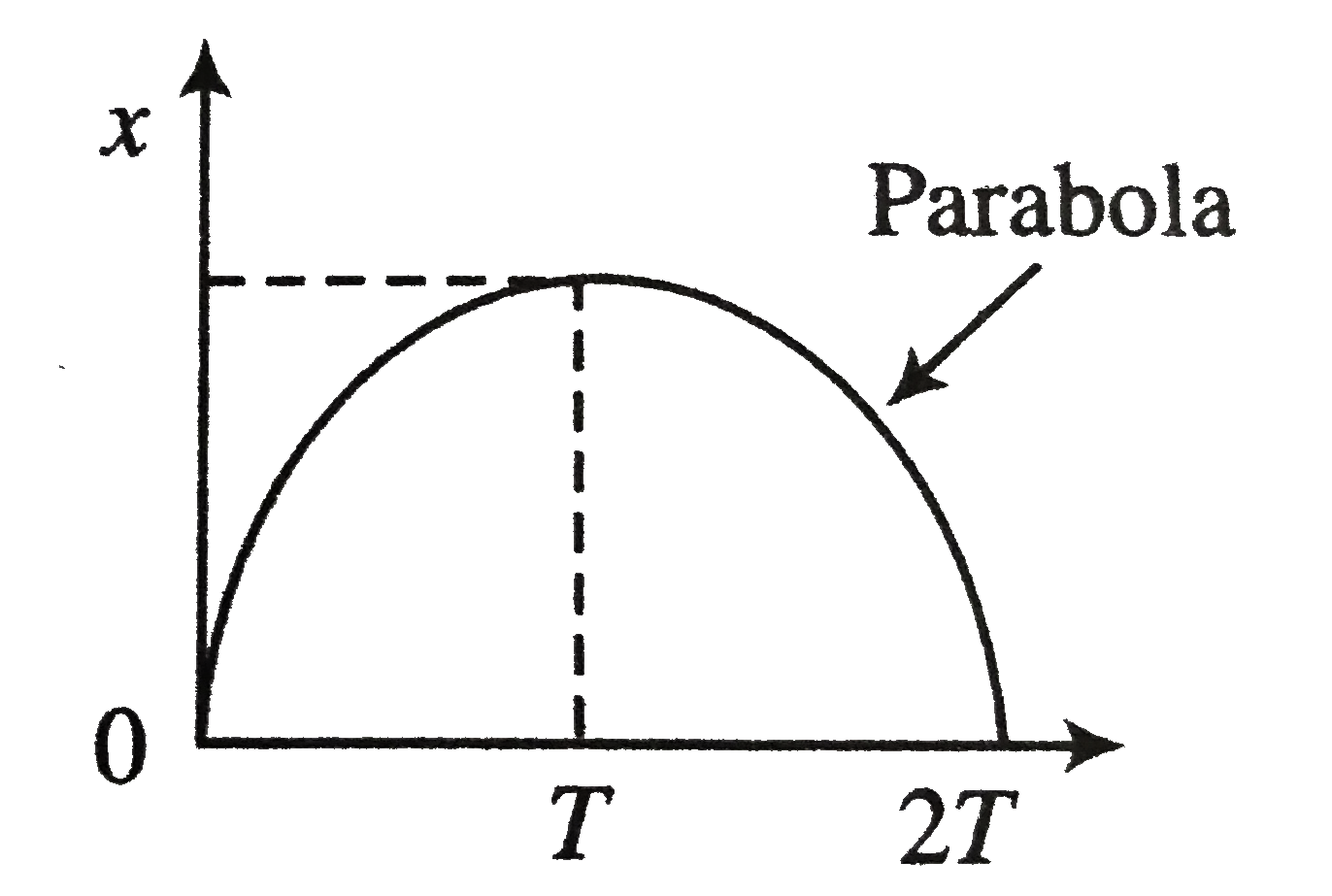
The a-t graph of the particle is correctly shown by06:08View SolutionThe x-t graph of a particle moving along a straight line is shown in figure

The speed-time graph of the particle is correctly shown by06:08View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

`vecv_(boat) = vecv_(boat,water) + vecv_(water)`.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.07:54View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
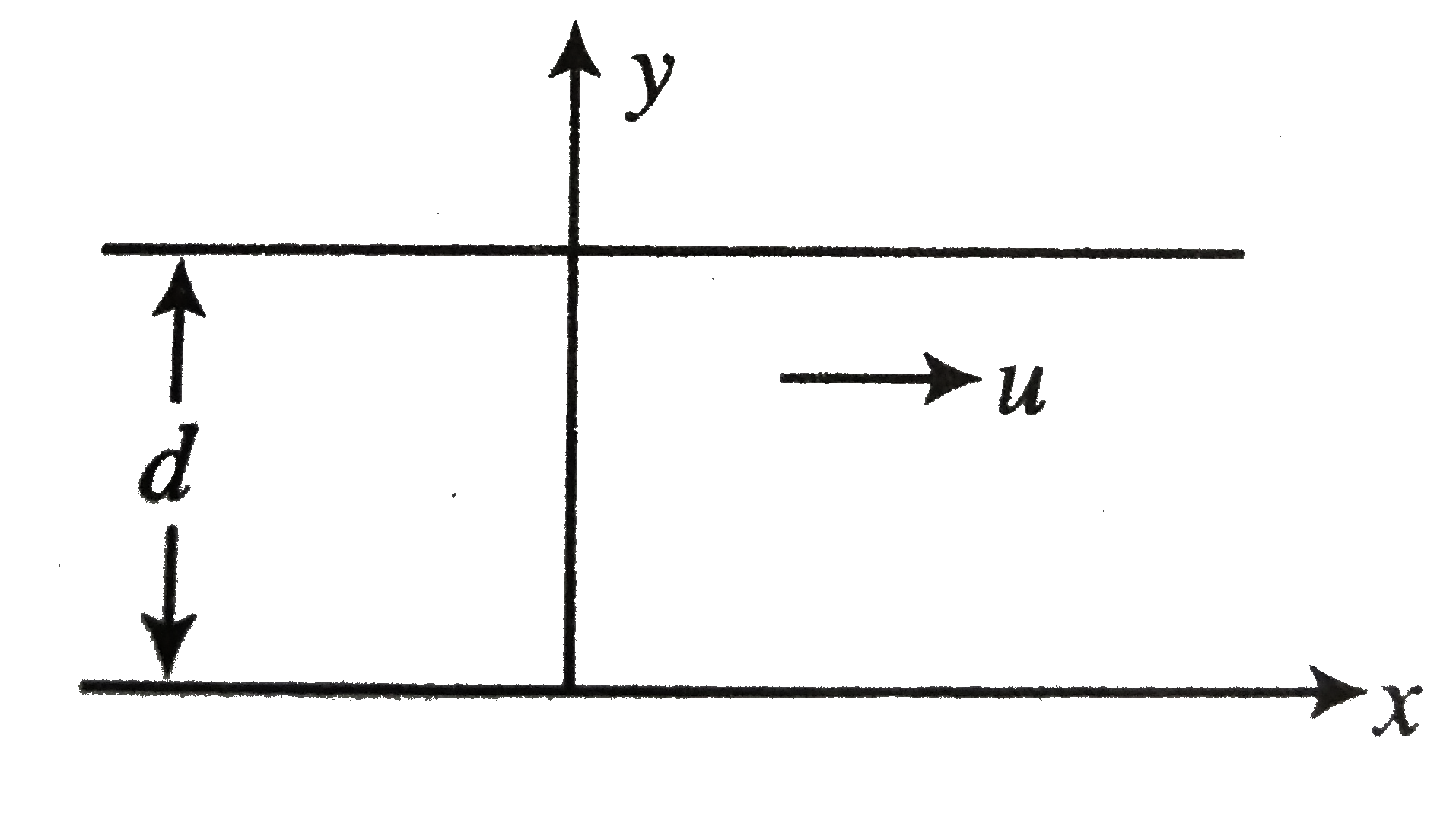
`vecv_(boat) = vecv_(boat,water) + vecv_(water)`.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.07:54View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

`vecv_(boat) = vecv_(boat,water) + vecv_(water)`.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.07:54View SolutionRam Shyam are walking on two perpendicular tracks with speed `3ms^(-1)` and `4 ms^(-1)`, respectively. At a certain moment `(say t = 0s)`, Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks.
During the motion the magnitude of velocity of ram with respect to Shyam is10:57View SolutionRam Shyam are walking on two perpendicular tracks with speed `3ms^(-1) and 4 ms^(-1)`, respectively. At a certain moment (say t = 0s), Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks.
Shortest distance between them subsequently is10:57View SolutionRam Shyam are walking on two perpendicular tracks with speed `3ms^(-1) and 4 ms^(-1)`, respectively. At a certain moment (say t = 0s), Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks.
The time t when they are at shortest distance from each other subsequently is -10:57View SolutionTwo graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take `g = 10 ms^(-2)`.
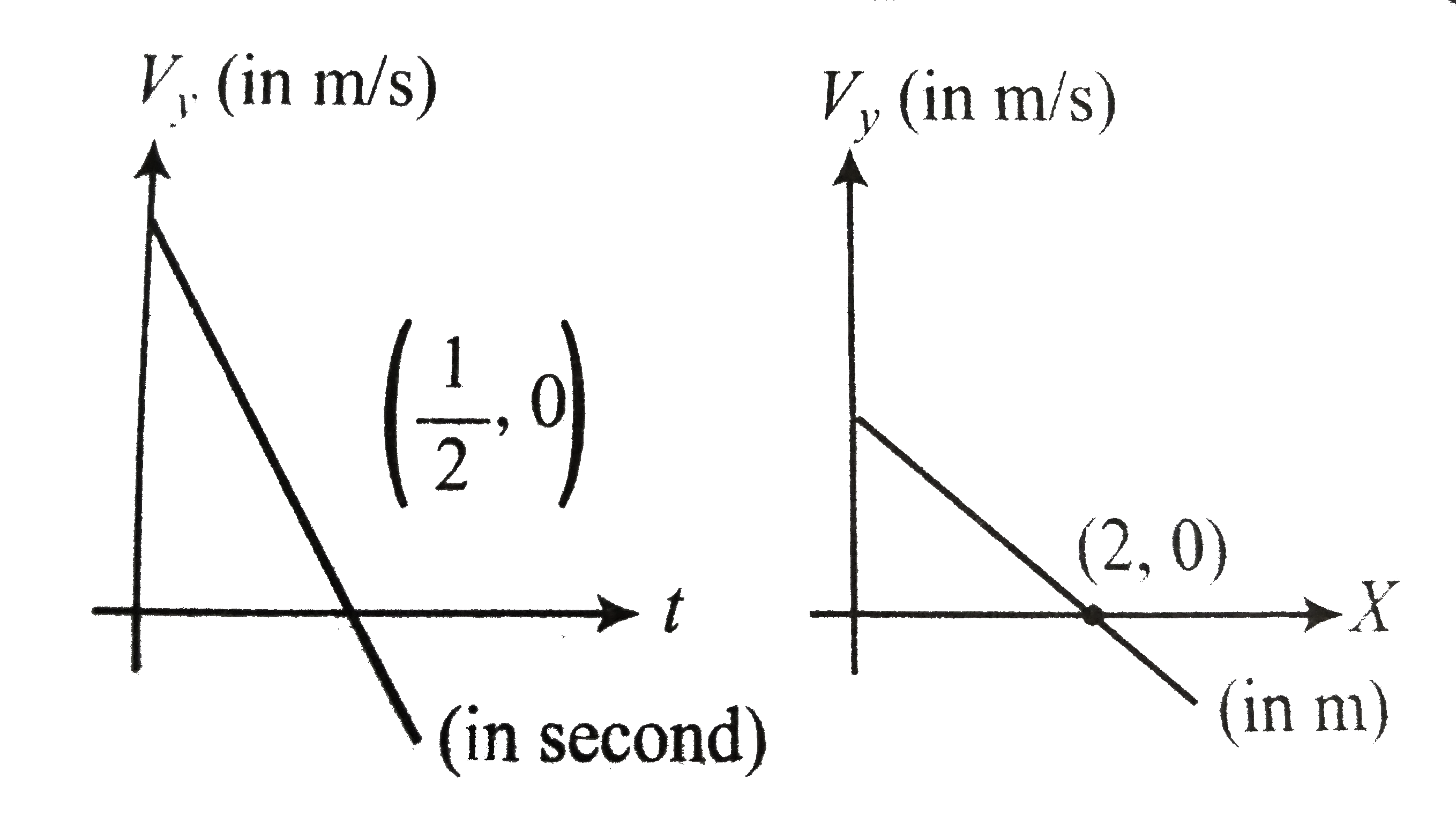 ,
,
The projection speed is :06:07View SolutionTwo graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take `g = 10 ms^(-2)`.
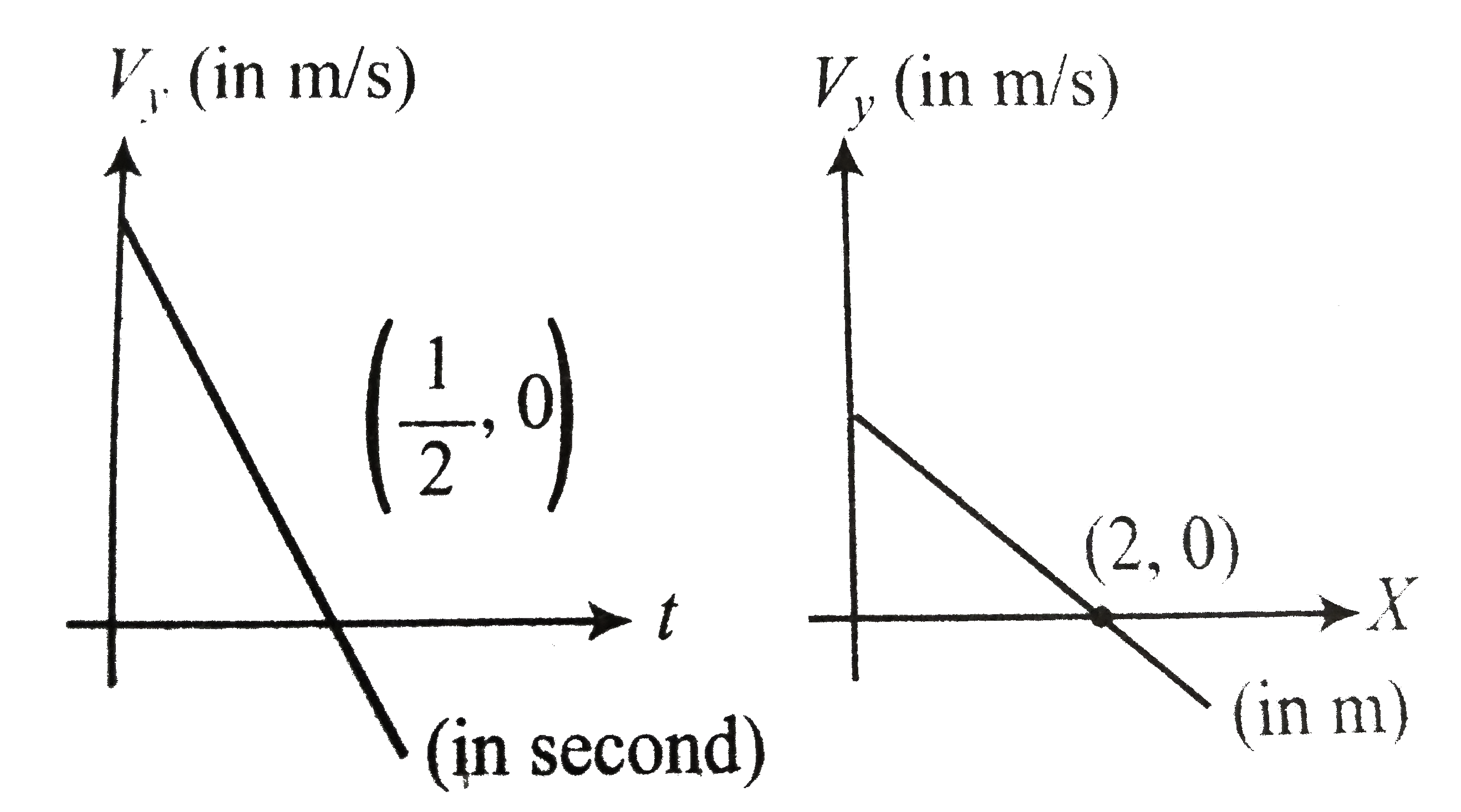
Projection angle with the horizontal is :06:07View SolutionTwo graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take `g = 10 ms^(-2)`.
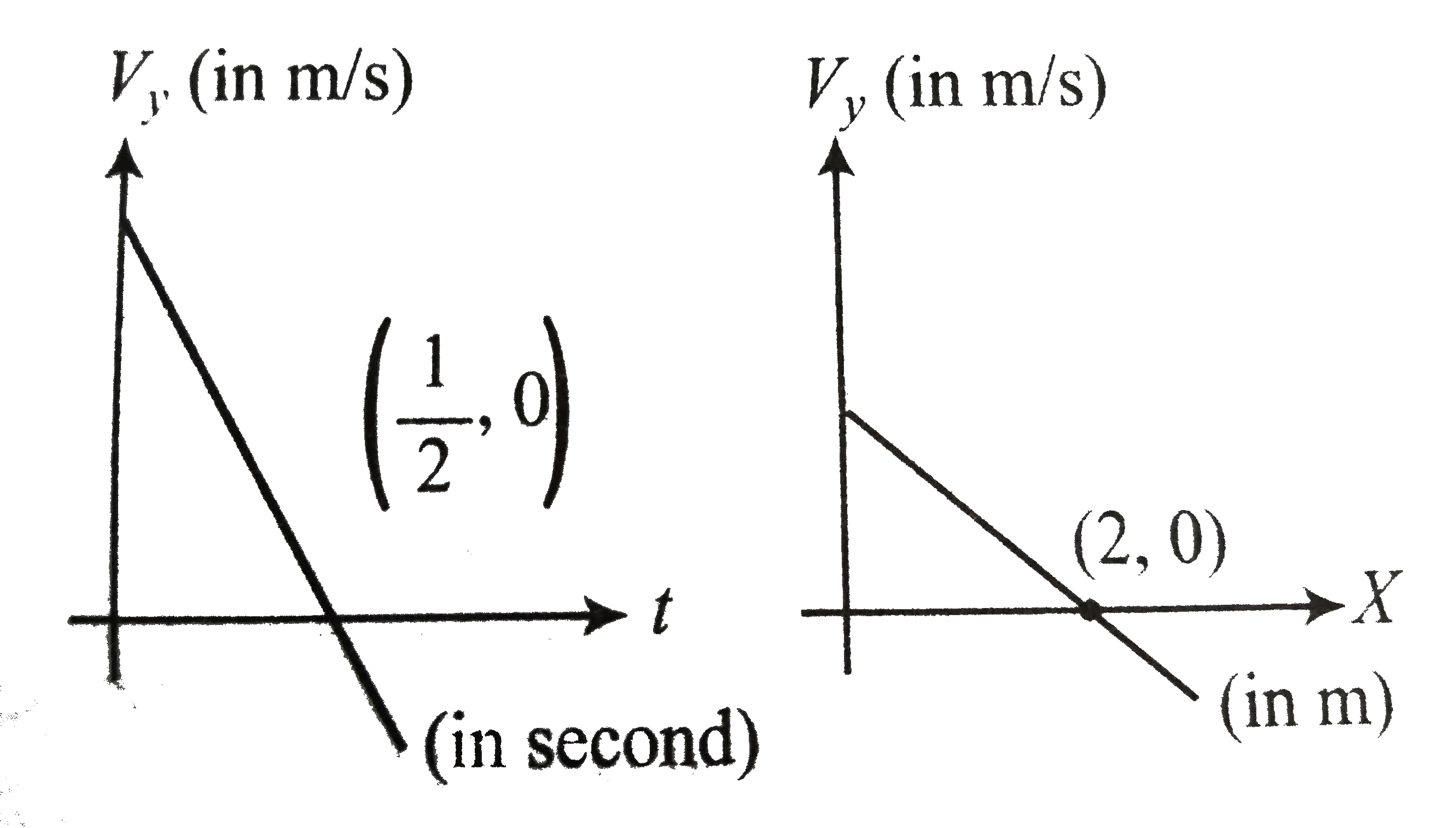 ,
,
Maximum height attained from the point of projection is06:07View Solution
Linked Comprehension Type questions and complete solutions for chapter MISCELLANEOUS KINEMATICS of CENGAGE PHYSICS (HINGLISH) of Class 11
