Complete Solutions to Single Correct Answer Type of chapter MISCELLANEOUS KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MISCELLANEOUS KINEMATICS |
| CENGAGE PHYSICS | Single Correct Answer Type |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
A particle is moving along the x-axis whose acceleration is given by ` a= 3x-4`, where x is the location of the particle. At t = 0, the particle is at rest at `x = 4//3m`. The distance travelled by the particles in 5 s is
View SolutionA point moves such that its displacement as a function of time is given by `x^3 = r^3 + 1`. Its acceleration as a function of time t will be
View SolutionThe acceleration of a particle starting from rest and travelling along a straight line is shown in figure. The maximum speed of the particle is
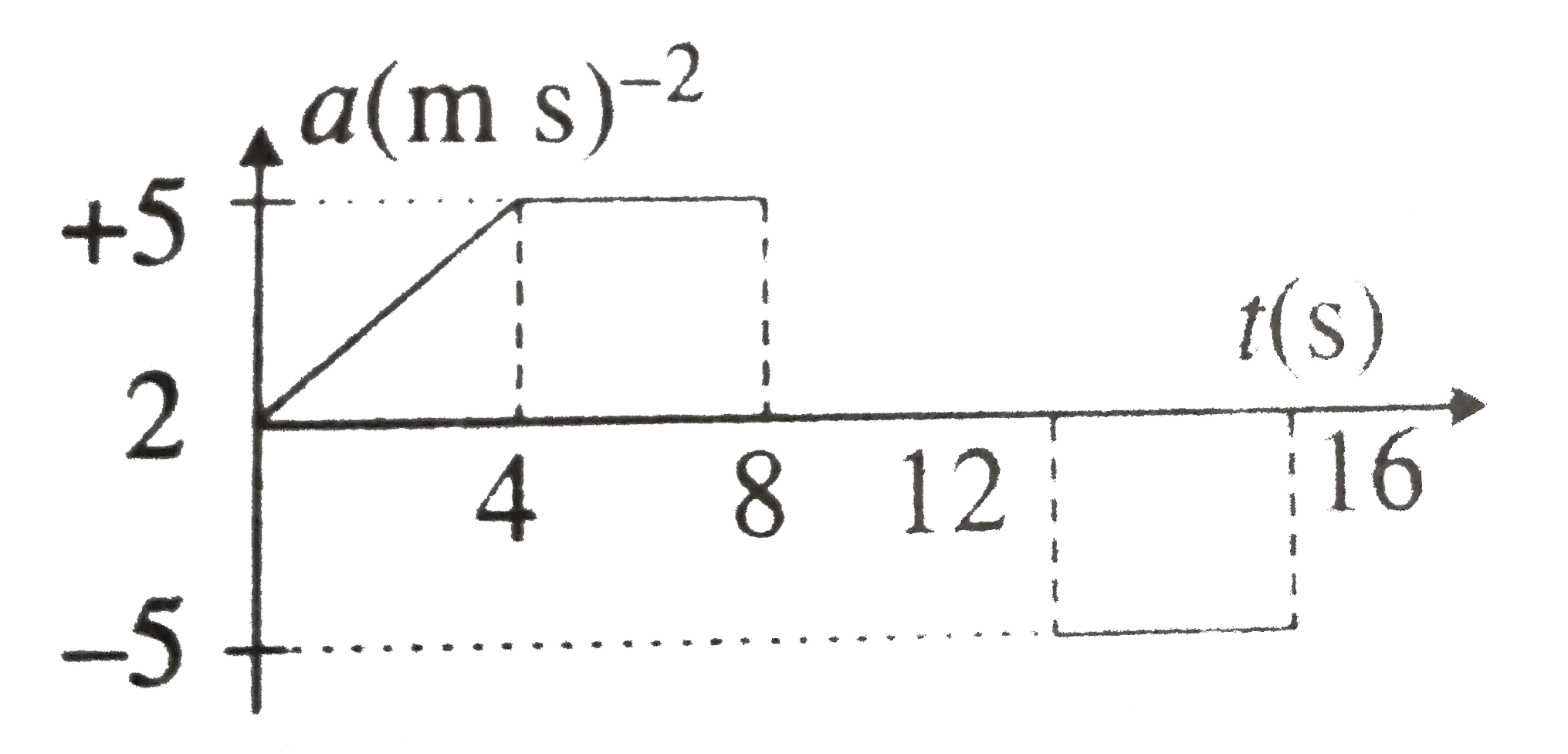
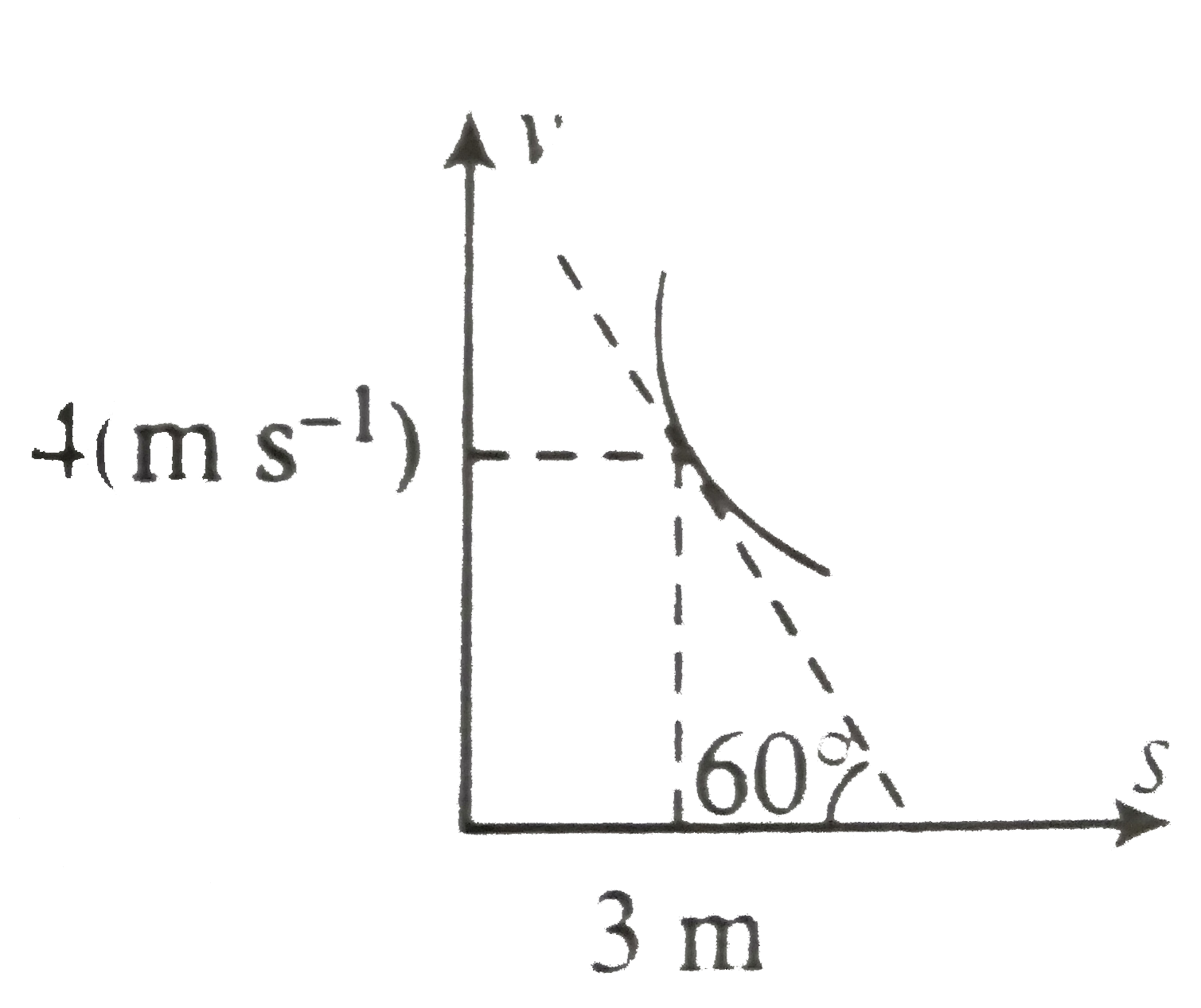
View SolutionA particle is moving along a straight line whose velocity - displacement graph is shown in figure. What is the acceleration when displacement is 3 m?
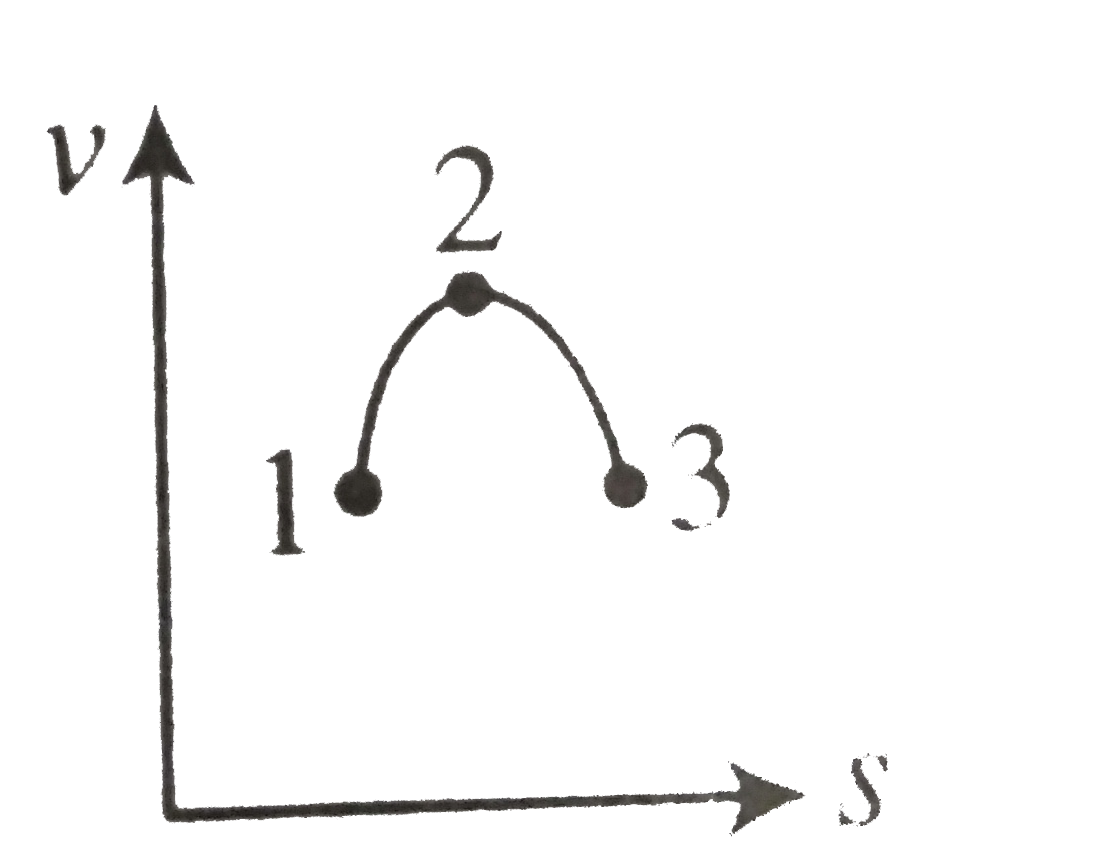
View SolutionFigure shows the velocity-displacement curve for an object moving along a straight line. At which of the points marked is the object speeding up?
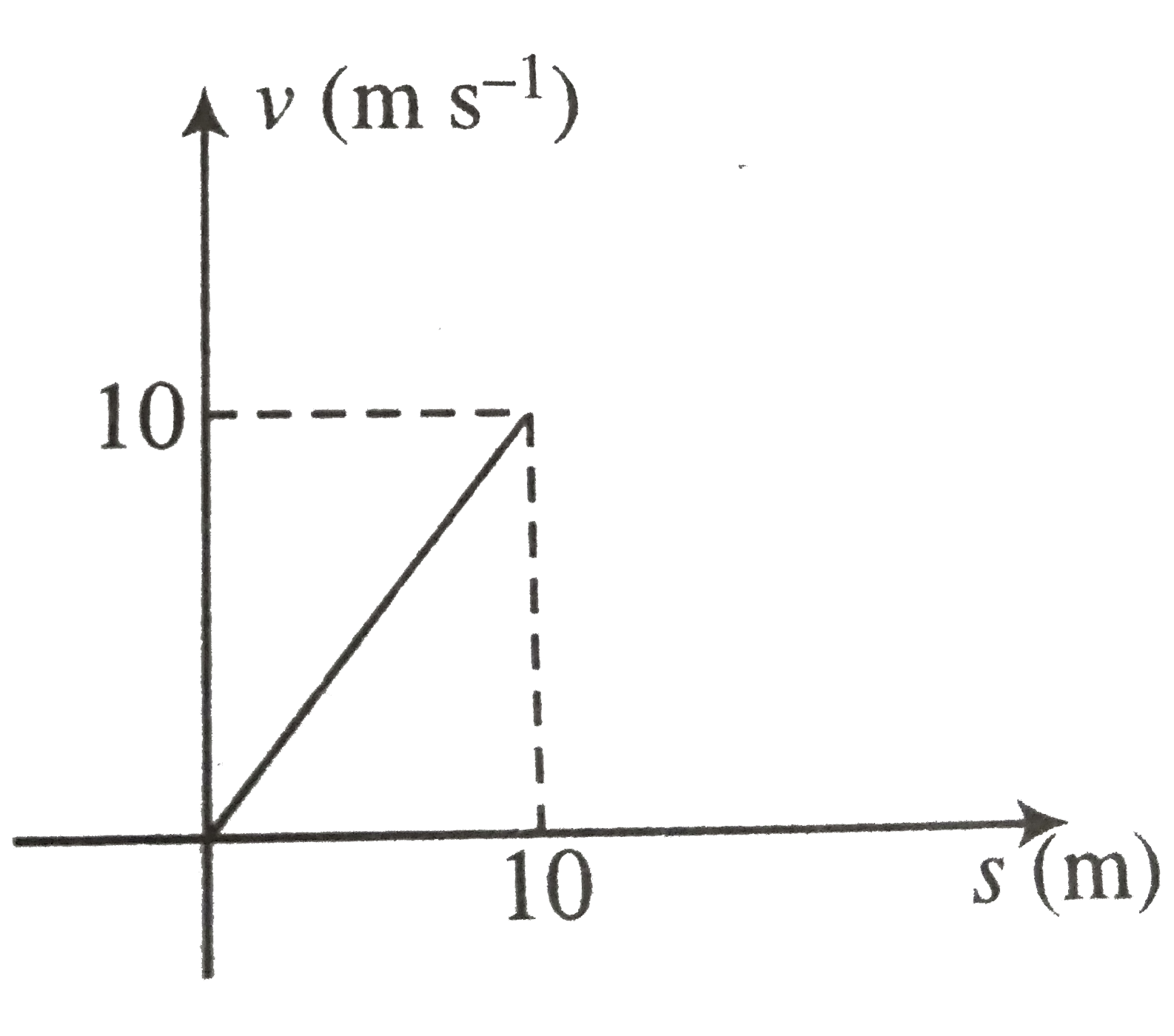
View SolutionVelocity versus displacement graph of a particle moving in a straight line as shown in figure.

The acceleration of the particle.
View SolutionVelocity versus displacement graph of a particle moving in a straight line as shown in figure.
The corresponding acceleration versus velocity graph will be .
View SolutionThe acceleration - velocity graph of a particle moving in a straight line is shown in figure. Then the slope of the velocity- displacement graph
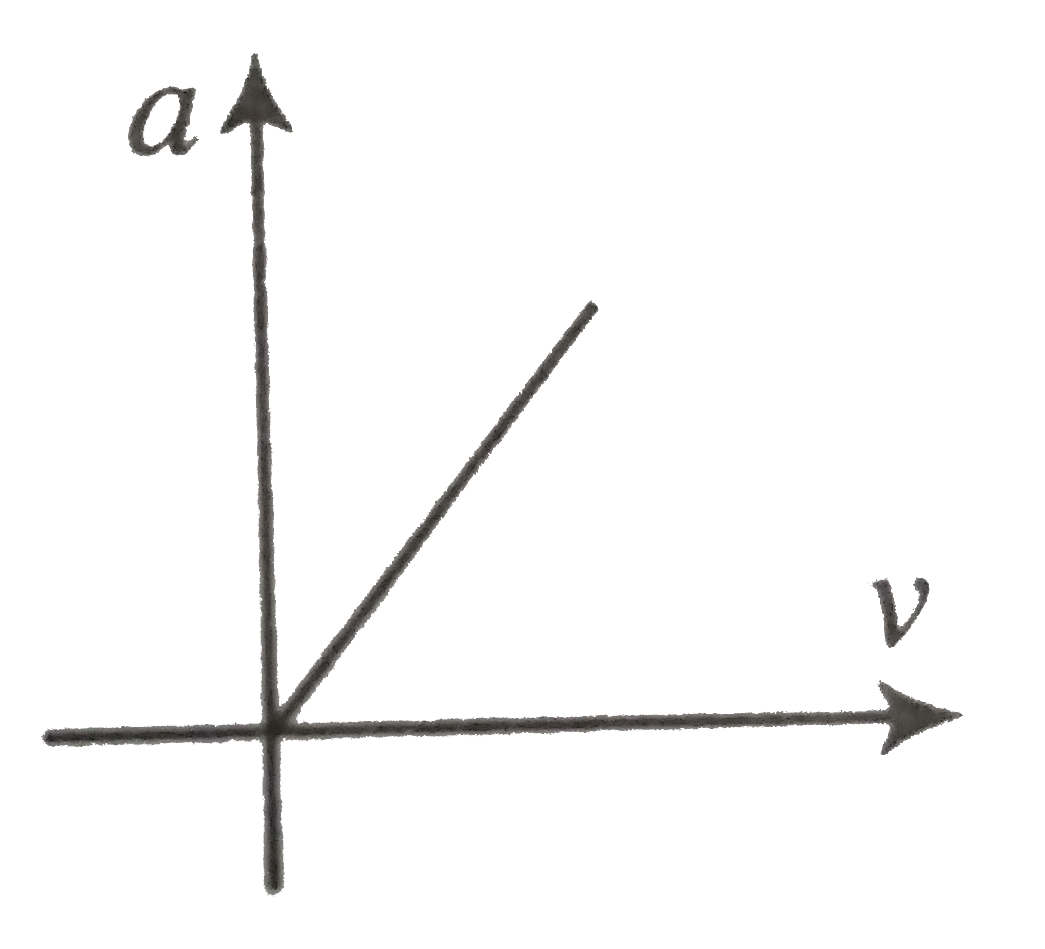
View SolutionA particle starts moving rectilinearly at time t = 0 such that its velocity v changes with time t according to the equation `v = t^2-t`, where t is in seconds and v is in `m s^(-1)`. The time interval for which the particle retrads (i.e., magnitude of velocity decreases)is
View SolutionAn object is moving in the x-y plane with the position as a function of time given by `vecr = x(t)hati + y(t)hatj`. Point O is at `x = 0 , y = 0` . The object is definitely moving towards O when
View SolutionAn object has velocity `vecv_1` w.r.t. ground. An observer moving with constant velocity `vecv_0` w.r.t. ground measures the velocity of the object as `vecv_2`. The magnitudes of three velocities are related by
View SolutionA man swimming downstream overcomes a float at a point M. After travelling distance D,he turned back and passed the float at a distance of `D//2` from the point M. Then the ratio of speed of swimmer with respect to still water to the speed of the river will be
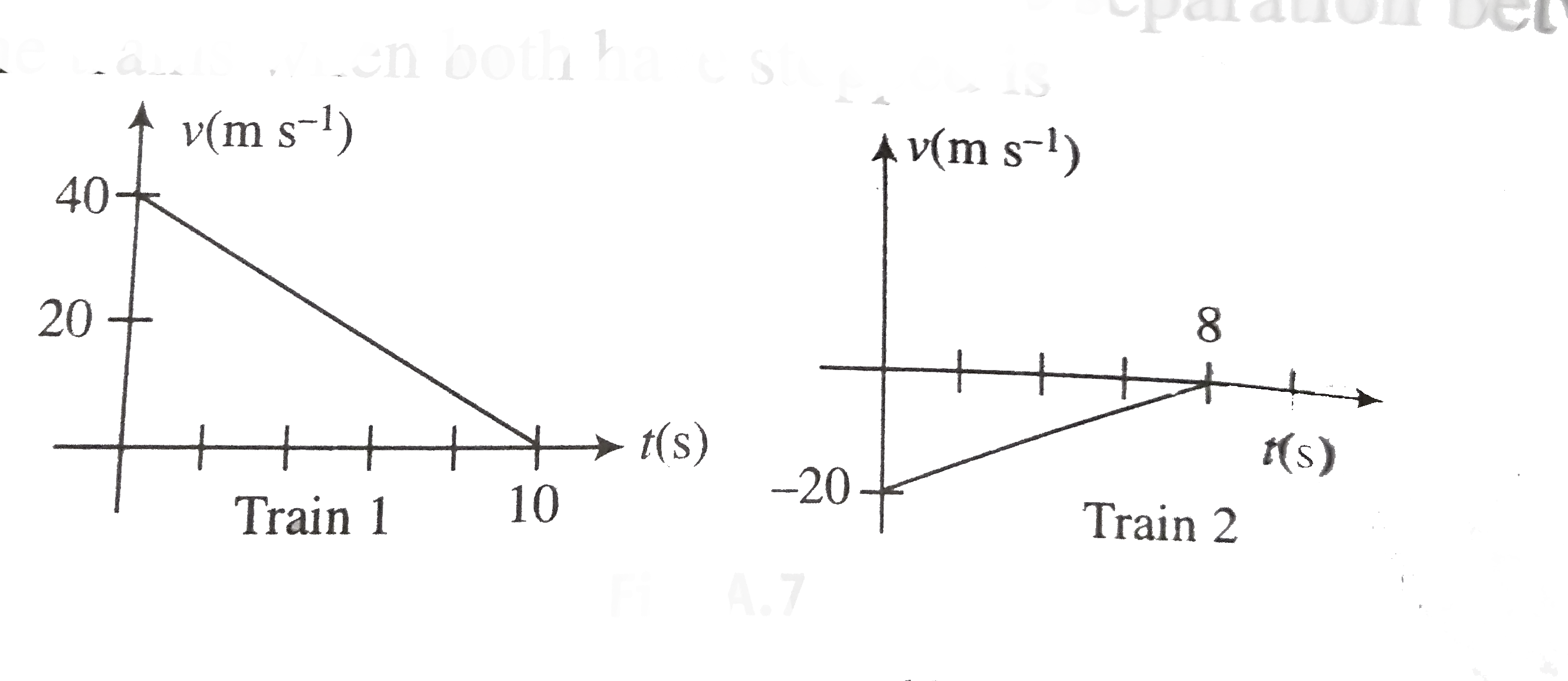
View SolutionTwo trains, which are moving along different tracks in opposite directions, are put on the same track due to a mistake. Their drivers, on noticing the mistake, start slowing down the trains when the trains are 300 m apart. Graphs given in figure show their velocities as function of time as the trains slow down. The separation between the trains when both have stopped is
View SolutionThe acceleration of a particle which moves along the positive x-axis varies with its position as shown in figure. If the velocity of the particle is `0.8 ms^(-1)` at x = 0, then velocity of the particle at `x = 1.4 m` is `(in ms^(-1))`.
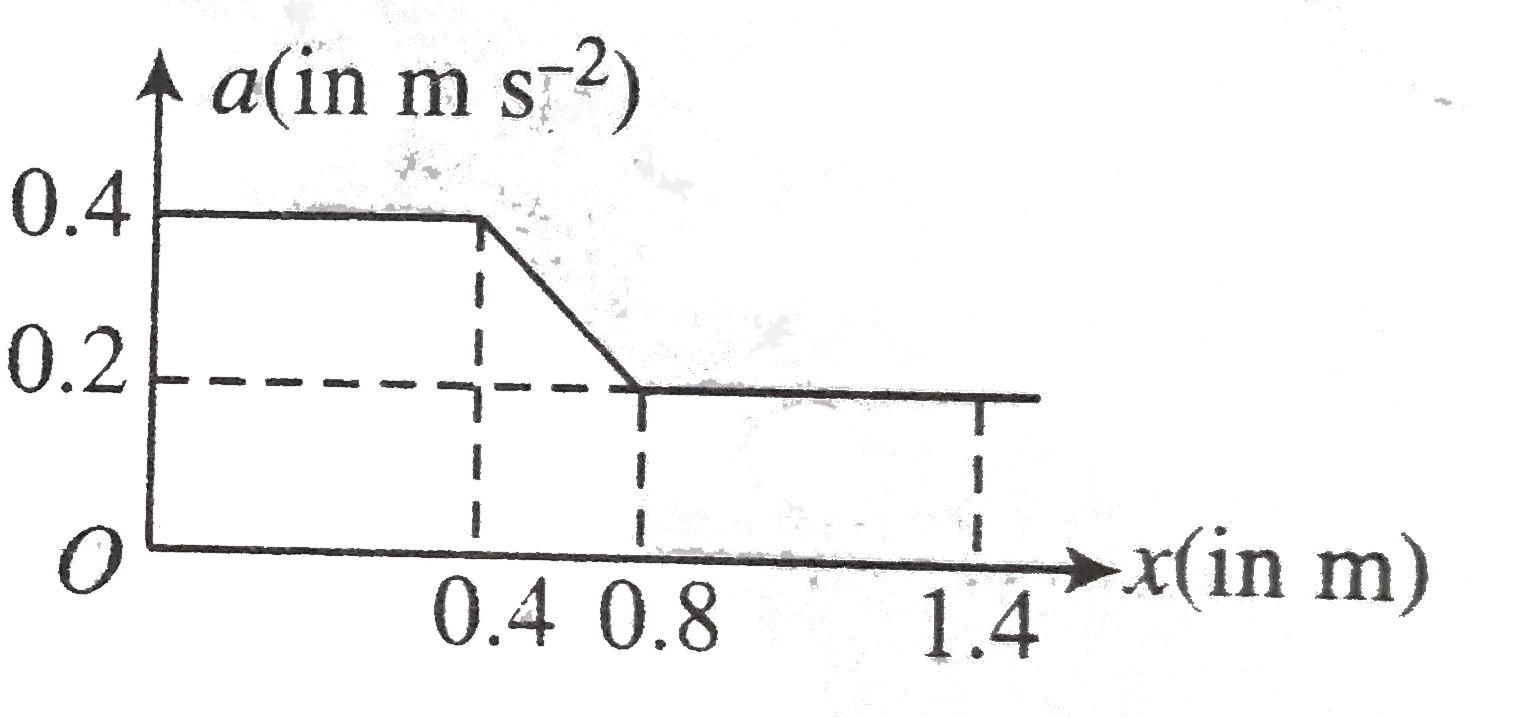
View SolutionSix particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
View SolutionThree boys are running on a equitriangular track with the same speed `5 ms^(-1)`. At start, they were at the three corners with velocity along indicated directions. The velocity of approach of any one of them towards another at `t = 10 s` equals

View SolutionTwo boys P and Q are playing on a river bank. P plans to swim across the river directly and come back. Q plans to swim downstream by a length equal to the width of the river and then come back. Both of them bet each other, claiming that the boy succeeding in less time will win. Assuming the swimming rate of both P and Q to the same, it can be concluded that
View SolutionA man holds an umbrella at `30^@` with the vertical to keep himself dry. He, then, runs at a speed of `10ms^(-1)`, and find the rain drops to be hitting vertically. Study the following statement and find the correct options.
i. Velocity of rain w.r.t. Earth is `20 ms^(-1)`
ii. Velocity of rain w.r.t. man is `10 sqrt(3)ms^(-1)`.
iii. Velocity of rain w.r.t. Earth is `30 ms^(-1)`
iv. Velocity of rain w.r. t. man is `10sqrt(2) ms^(-1)` .
View SolutionRain appears to fall vertically to a man walking at `3kmh^(-1)`, but when he changes his speed to double, the rain appears to fall at `45^@` with vertical. Study the following statements and find which of them are correct.
i. Velocity of rain is `2 (sqrt3) kmh^(-1)`.
ii. The angle of fall of rain (with vertical) is `theta = tan^(-1)(1/(sqrt2)).`
iii. The angle of fall of rain (with vertical) is `theta = sin^(-1) (1/(sqrt2))`.
iv. Velocity of rain is `3(sqrt2)kmh^(-1)` .
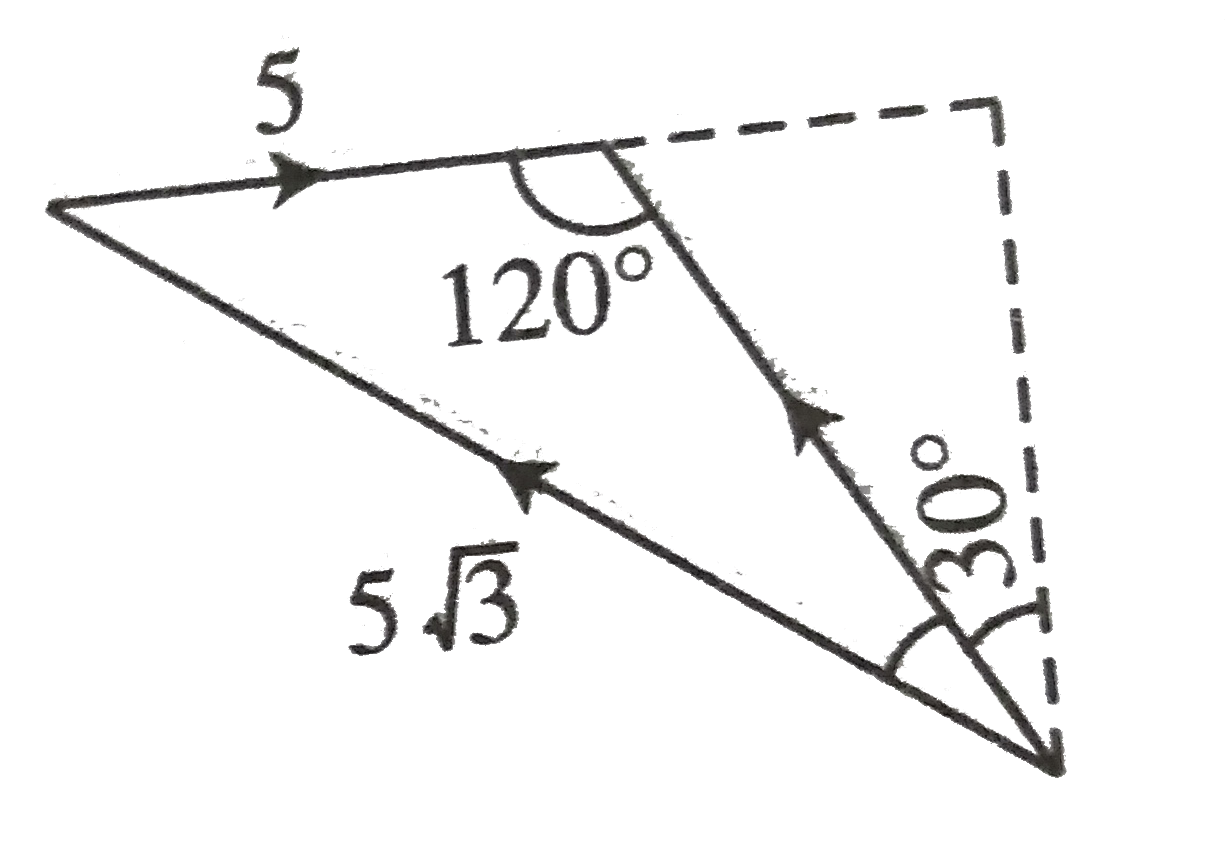
View SolutionA motor boat is to reach at a point `30^@` upstream on the outer side of a river flowing with velocity `5 ms^(-1)`. The velocity of motor boat with respect to water is `5(sqrt3) ms^(-1)`. The driver should steer the boat at an angle.
View SolutionThe raindrops are hitting the back of a man walking at a speed of `5km//hr`. If he now starts running in the same direction with a constant acceleration, the magnitude of the velocity of the rain with respect to him will
View SolutionA body A is thrown vertically upwards with such a velocity that it reaches a maximum height of h. Simultaneously, another body B is dropped from height h. It strikes the ground and does not rebound. The velocity of A relative to B versus time graph is best represented by (upward direction is positive).
View SolutionA particle is projected with velocity u at angle `theta` with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionTwo particles are projected simultaneously from the same point, with the same speed, in the same vertical plane, and at different angles with the horizontal in a uniform gravitational field acting vertically downwards. A frame of reference is fixed to one particle. The position vector of the other particle , as observed from this frame, is `vecr`. Which of the following statement is correct?
View SolutionTwo particles are thrown horizontally in opposite directions with velocities u and 2u from the top of a high tower. The time after which their radius of curvature will be mutually perpendicular is
View SolutionIn figure, the angle of inclination of the inclined plane is `30^@`. Find the horizontal velocity `V_0` so that the particle hits the inclined plane perpendicularly.
 .
.
View SolutionA particle reaches its highest point when it has covered exactly one half of its horizontal range. The corresponding point on the displacement -time graph is charecterized by :
View SolutionTwo particles A and B are placed as shown in figure. The particle A, on the top of tower, is projected horizontally with a velocity u and particle B is projected along the surface towards the tower, simultaneously. If both particles meet each other, then the speed of projection of particles B is [ignore any friction]
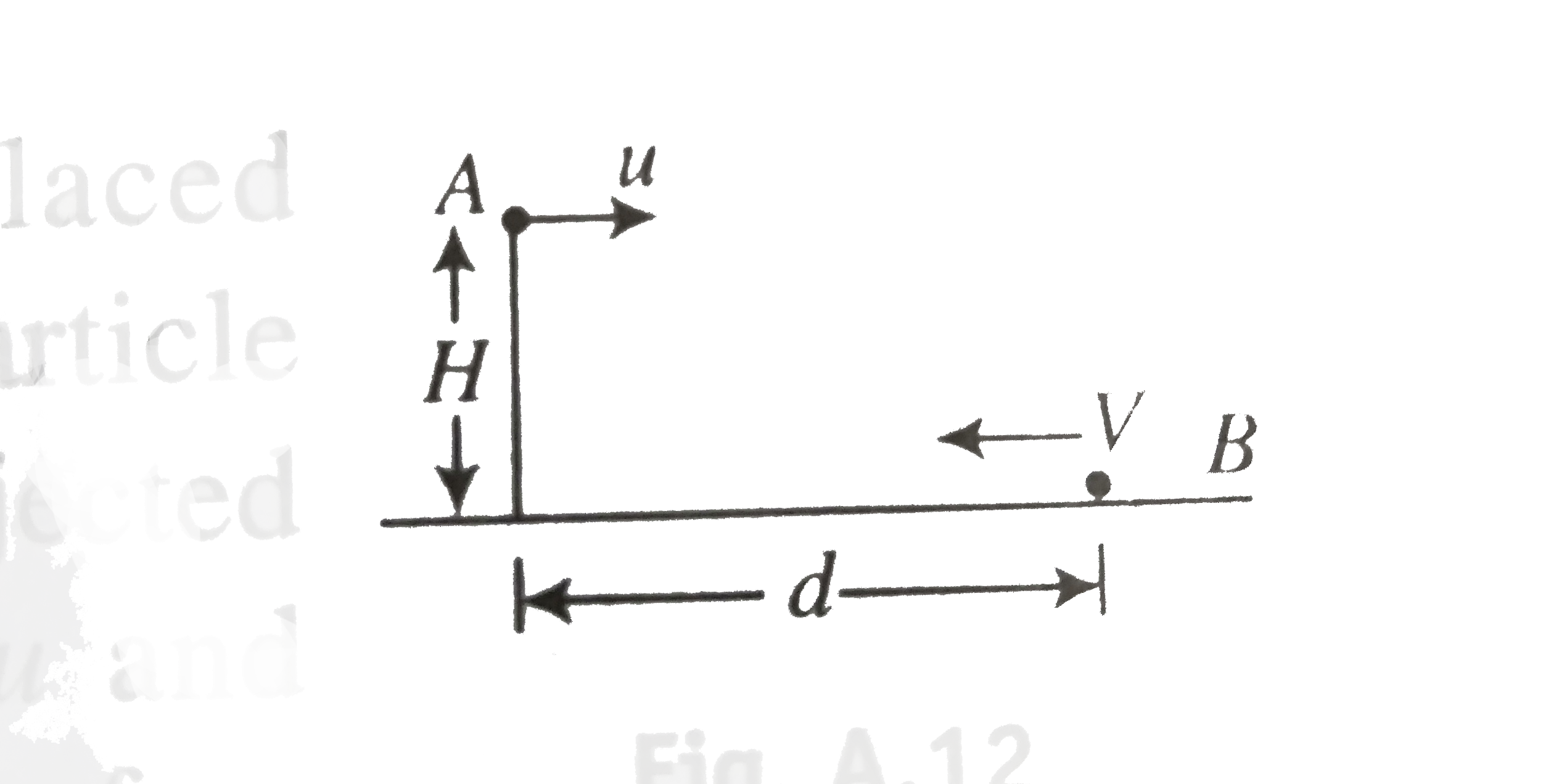
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle `theta` with the horizontal. The range of the projectile along the inclined plane is

View SolutionA ball rolls off the top of a staircase with a horizontal velocity `u m//s`. If the steps are h meter high and b meter wide, the ball will hit the edge of the nth steps, if:
View SolutionThe maximum range of a projectile is 500m. If the particle is thrown up a plane is inclined at an angle of `30^(@)` with the same speed, the distance covered by it along the inclined plane will be:
View SolutionA cannon fires a projectile as shown in figure. The dashed line shows the trajectory in the absence of gravity. The points M,N, O, and P correspond to time at `t = 0, 1 s, 2 s`, and `3` s, respectively. The length of X,Y, and Z are , respectively.
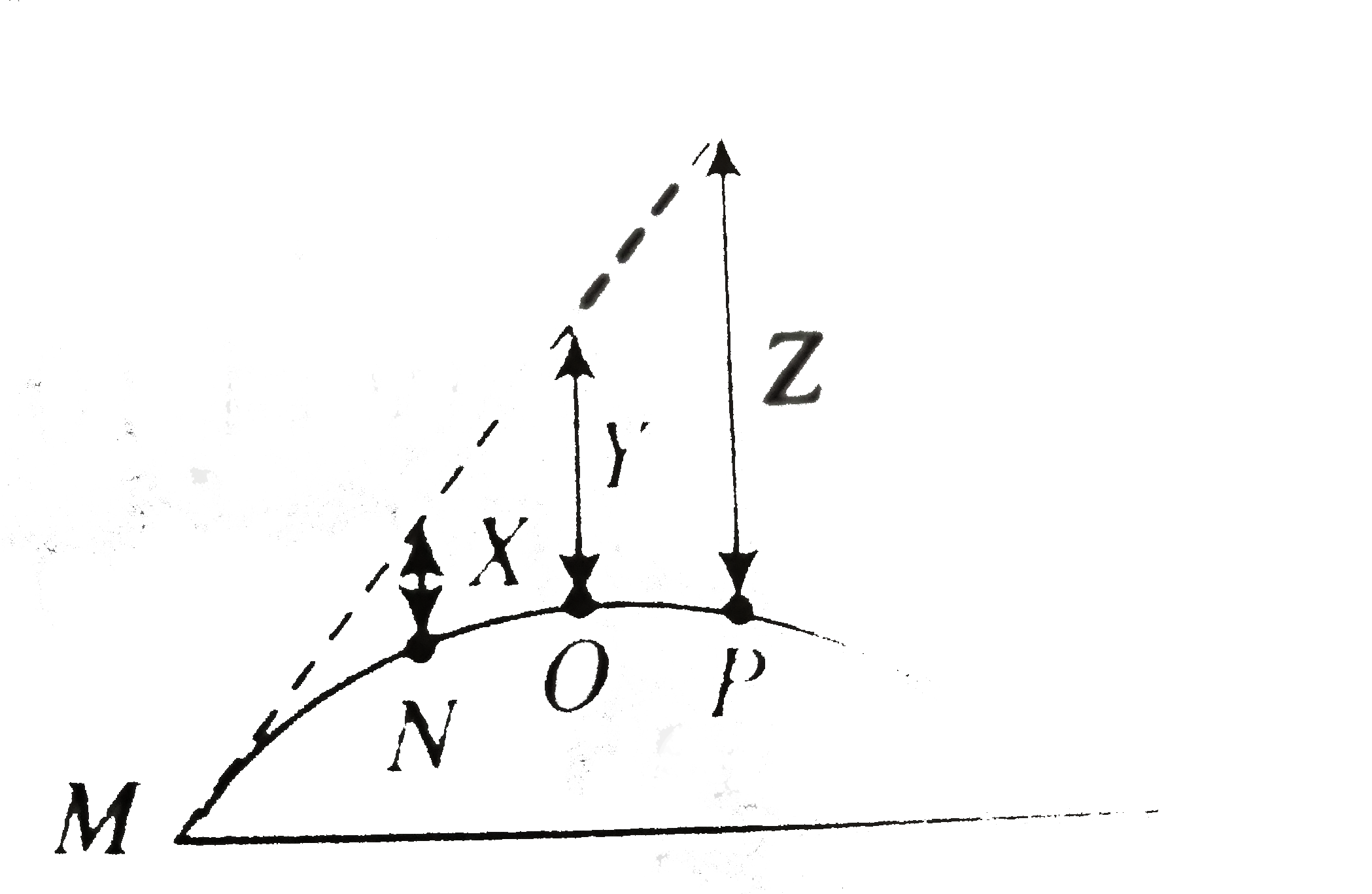 .
.
View SolutionThe speed of a projectile at its highest point is `v_1` and at the point half the maximum height is `v_2`. If `v_1/v_2 = sqrt(2/5)`, then find the angle of projection.
View SolutionA particle is projected at an angle of elevation `alpha` and after t second it appears to have an elevation of `beta` as seen from the point of projection. Find the initial velocity of projection.
View SolutionShots are fired simultaneously from the top and bottom of a vertical cliff with the elevation `alpha = 30^@`, beta `= 60^@`, respectively. The shots strike an object simultaneously at the same point. If `a = 10 (sqrt3)` m is the horizontal distance of the object from the cliff, then the height h of the cliff is

View SolutionFigure shows that particle A is projected from point P with velocity u along the plane and simultaneously another particle B with velocity v at an angle `alpha` with vertical. The particles collide at point Q on the plane. Then
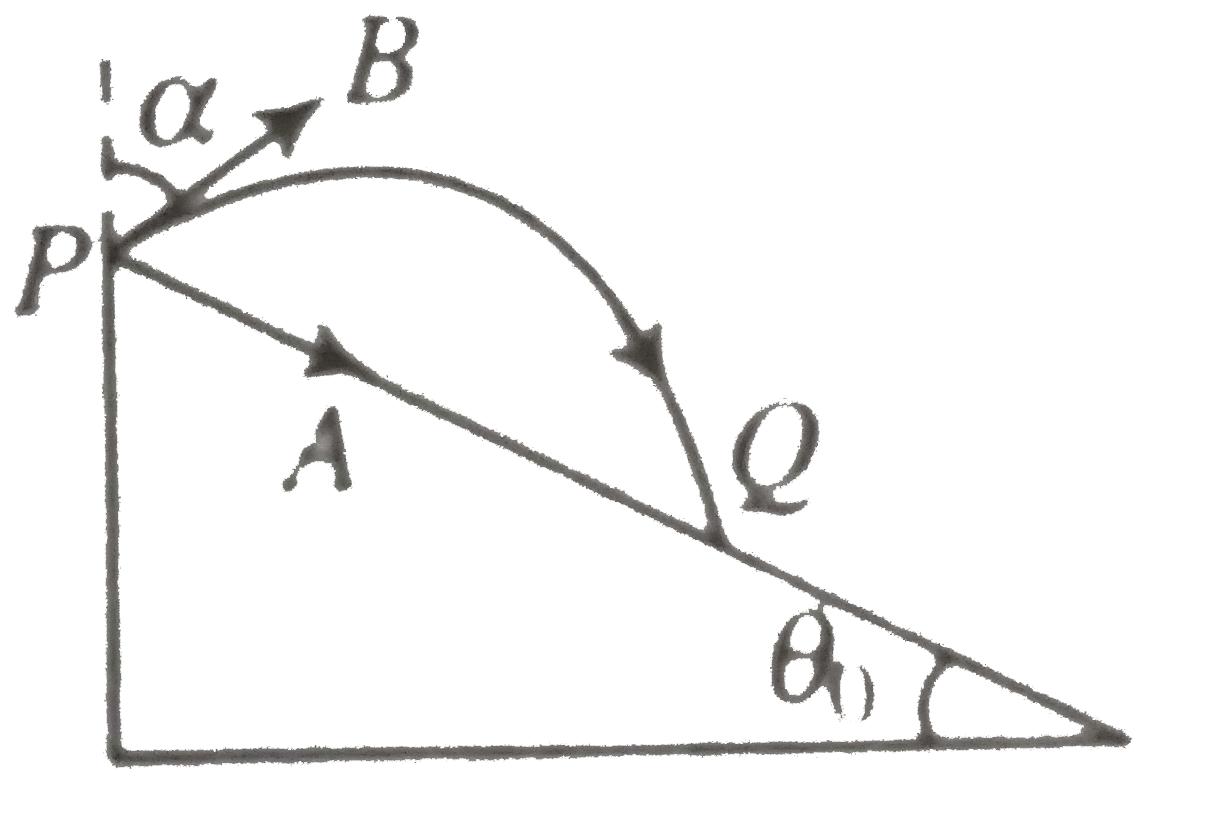
View SolutionA platform is moving upwards with an accelerations of `5ms^(-2)`. At the moment when its velocity is ` u = 3ms^(-1)`, a ball is thrown from it with a speed of `30 ms^(-1)` w.r.t. platform at an angle of `theta = 30^@` with horizontal. The time taken by the ball to return to the platform is
View SolutionTwo balls are projected from points A and B in vertical plane as shown in figure. AB is a straight vertical line. The balls can collide in mid air if `v_1//v_2` is equal to
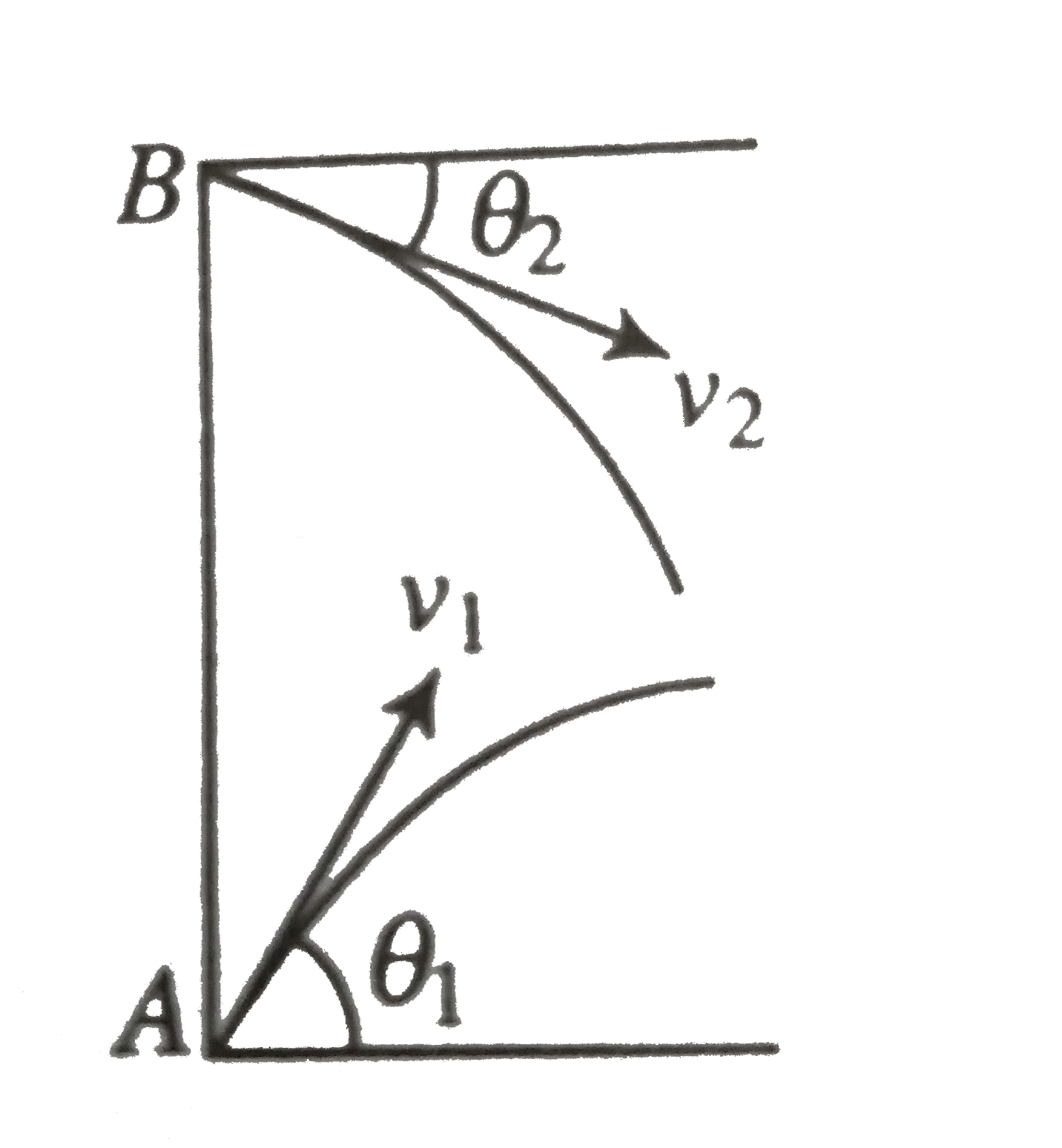
View SolutionA particle is thrown at time t = 0 with a velocity of `10 ms^(-1)` at an angle `60^@` with the horizontal from a point on an inclined plane, making an angle of `30^@` with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is

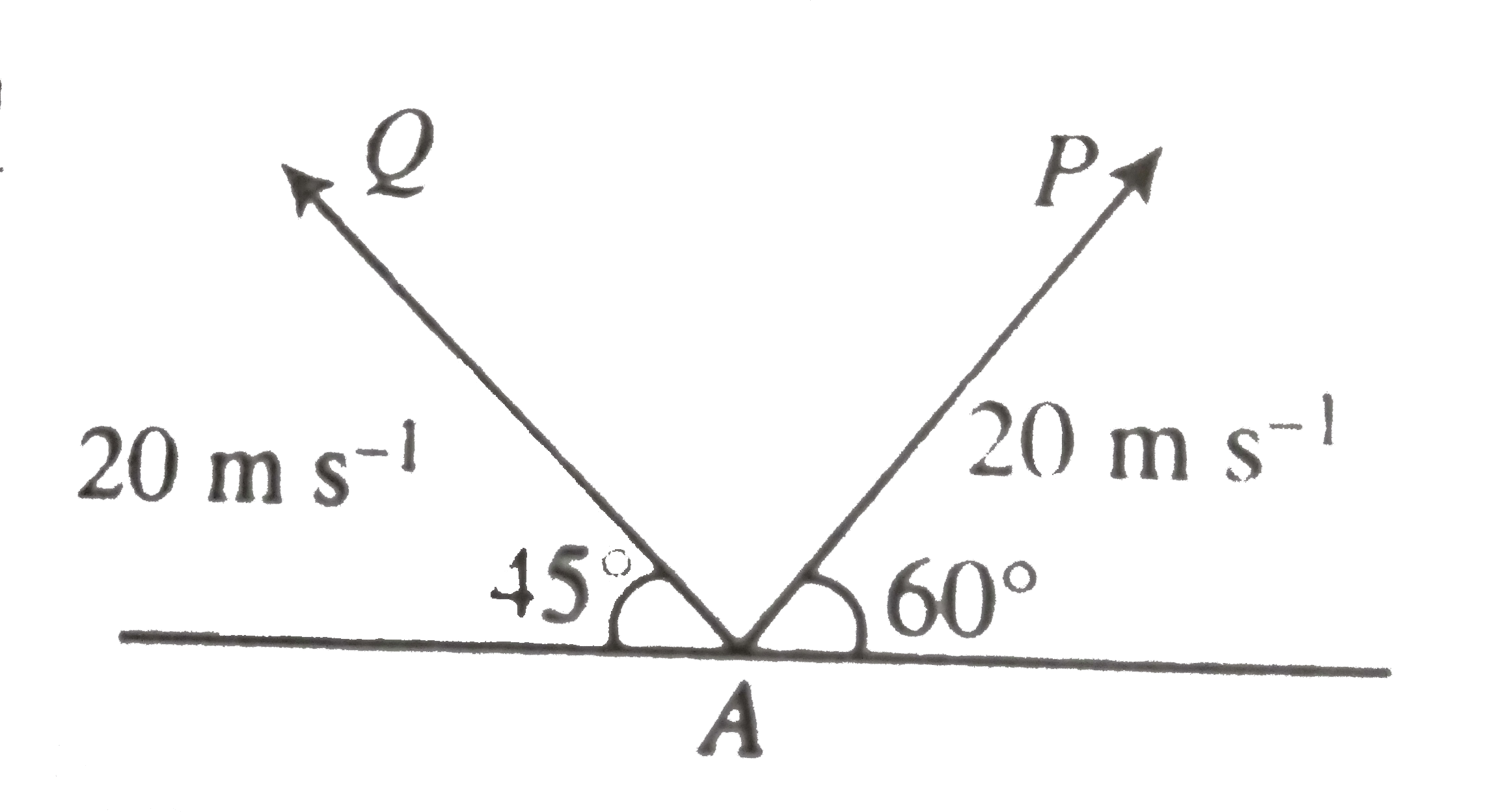
View SolutionTwo particles P and Q are projected simultaneously away from each other from a point A as shown in figure. The velocity of P relative to Q in `ms^(-1)` at the instant when the motion of P is horizontal is
View SolutionFigure shows the velocity and acceleration of a point line body at the initial moment of its motion. The acceleration vector of the body remains constant. The minimum radius of curvature of trajectory of the body is

View SolutionFigure shows path followed by a particle and position of a particle at any instant. Four different students have represented the velocity vectors and acceleration vectors at the given instant. Which vector diagram can not be true in any situation? (In each figure velocity is tangential to the trajectory).
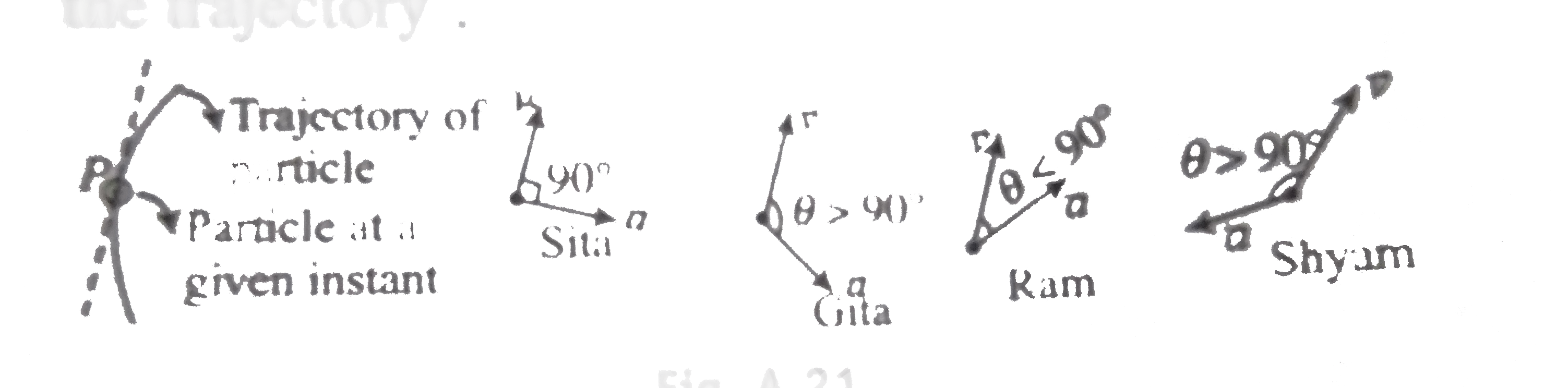
View SolutionA car is moving in east direction. It takes a right turn and moves along south direction without change in its speed. What is the direction of average acceleration of the car?
View SolutionTwo guns on a battleship simultaneously fire two shells with same speed at enemy ships. If the shells follow the parabolic trajectories as shown in figure. Which ship will get hit first?

View SolutionThe initial and final velocities of an object are as shown in figure. Which arrows shown in figure can be represent average acceleration vector?

View SolutionTwo identical balls are set into motion simultaneously from an equal height `h`. While ball `A` is thrown horizontally with velocity `v`, ball `B` is just released to fall by itself. Choose the alternative that best represents the motion of `A` and `B` with respect to an observer who moves with velocity `v//2` with respect to the ground as shown in the figure.

View SolutionAn aeroplane is flying vertically upwards. When it is at a height of `1000 m` above the ground and moving at a speed of `367 m//s`., a shot is fired at it with a speed of 567 `ms^(-1)` from a point directly below it. What should be the acceleration of aeroplane so that it may escape from being hit?
View SolutionJai is standing on the top of a building of height 25 m he wants to throw his gun to Veeru who stands on top of another building of height 20 m at distance 15 m from first building. For which horizontal speed of projectile, it is possible?
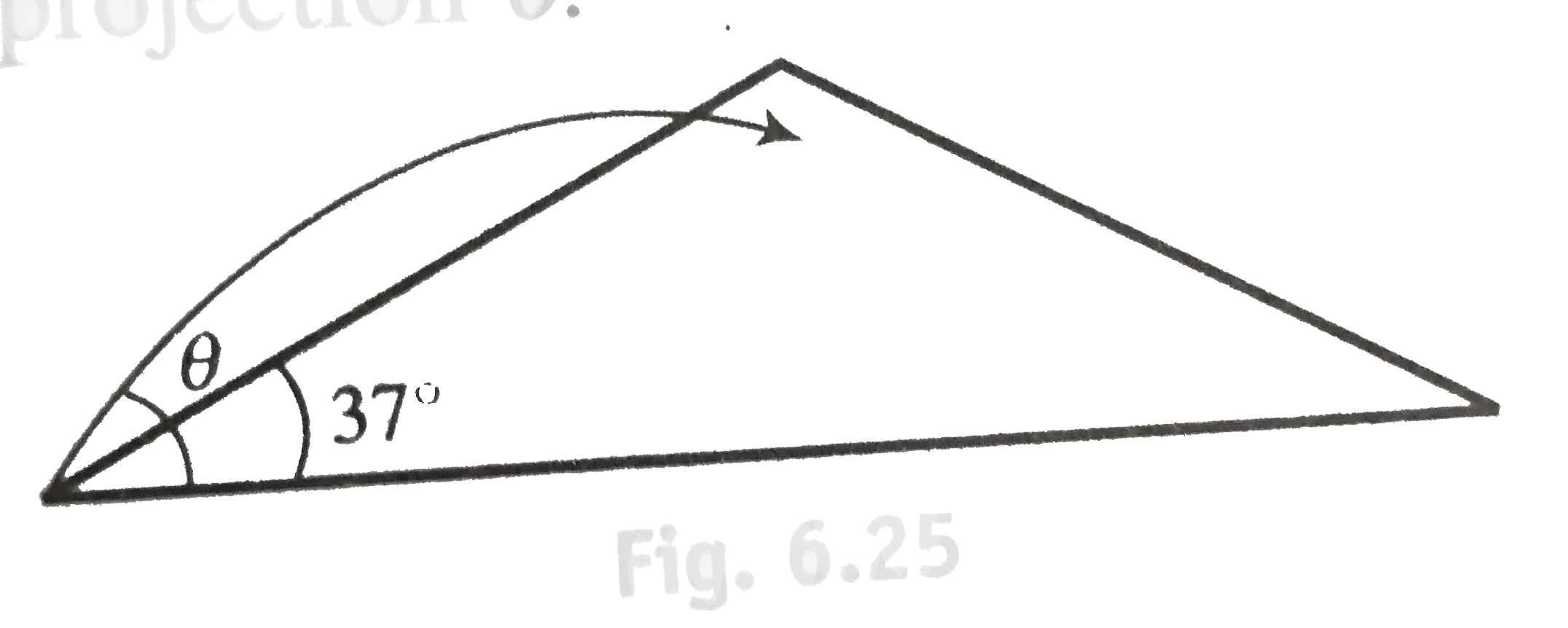
View SolutionA shot is fired at an angle `theta` to the horizontal such that it strikes the hill while moving horizontally. Find the initial angle of projection `theta`.
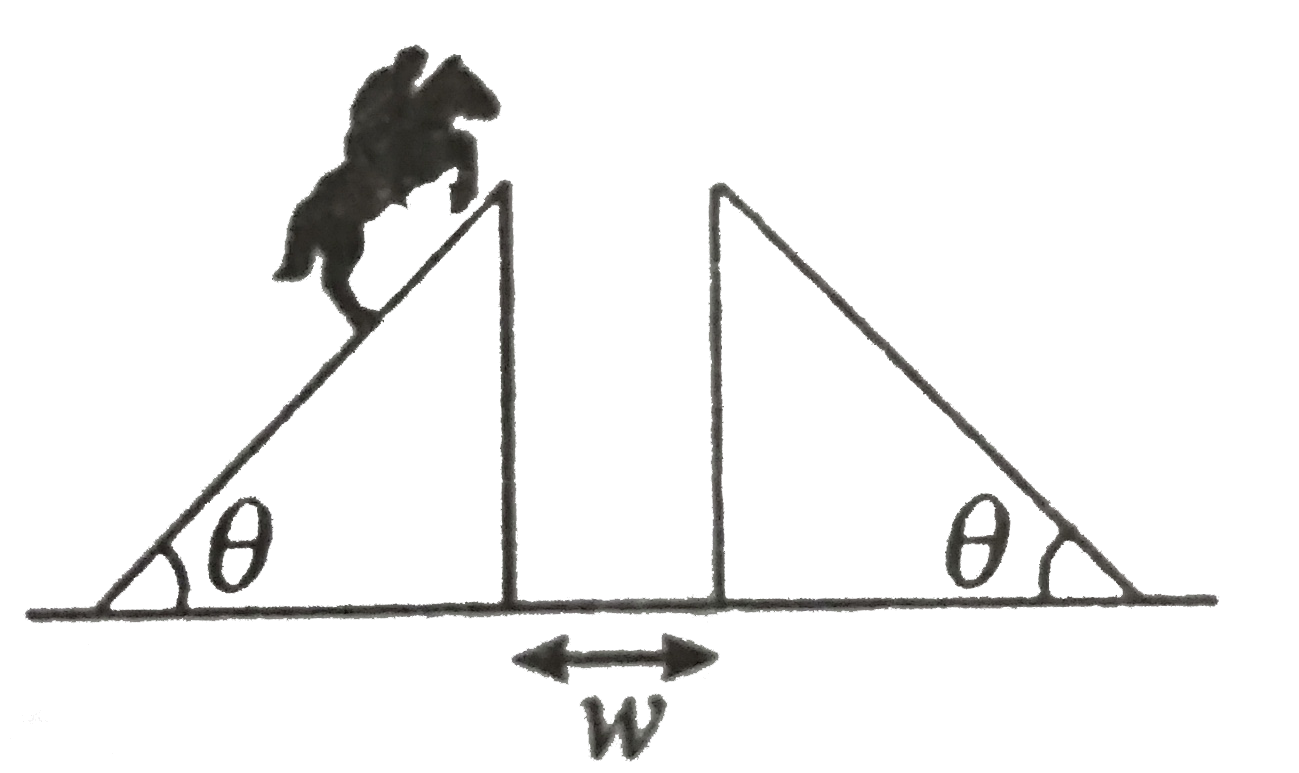
View SolutionA man is riding on a horse. He is trying to jump the gap between two symmetrical ramps of snow separated by a distance W as shown in figure. He launches off the first ramp with a speed `v_L`. The man and the horse have a total mass m. and their size is small as compared to W. The value of initial launch speed `V_(L)` which will put the horse exactly at the peak of the second ramp is
View SolutionA particle is moving eastwards with a velocity of ` 5 ms_(-1)`. In `10 seconds` the velocity changes to `5 ms^(-1)` northwards. The average acceleration in this time is
View SolutionA river is flowing from west to east at a speed of ` 5 metres per minute` . A man on the south bank of the river , capable of swimming at `10 metres per minute`, in still water , wants to swim across the river in the shortest time . He should swim in a direction
View SolutionA boat which has a speed of `5 km// hr ` in steel water crosses a river of width ` 1 km` along the shortest possible path in `15 minutes`. The velocity of the river water in ` km// hr` is
View SolutionIn `1.0 s`, a particle goes from point `A` to point `B` , moving in a semicircle of radius `1.0 m ` (see figure ). The magnitude of the average velocity
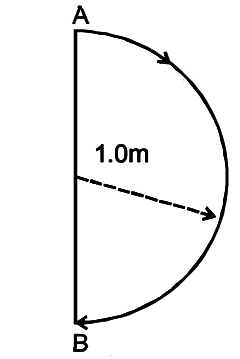
View SolutionA ball is dropped vertically from `a` height `d` above the ground . It hits the ground and bounces up vertically to a height ` (d)//(2). Neglecting subsequent motion and air resistance , its velocity `v` varies with the height `h` above the ground as
View SolutionA particle starts sliding down a frictionless inclined plane. If ` S_(n) ` is the distance travelled by it from time ` t = n-1 sec `, to `t = n sec`, the ratio ` (S_(n))/(s_(n+1))` is
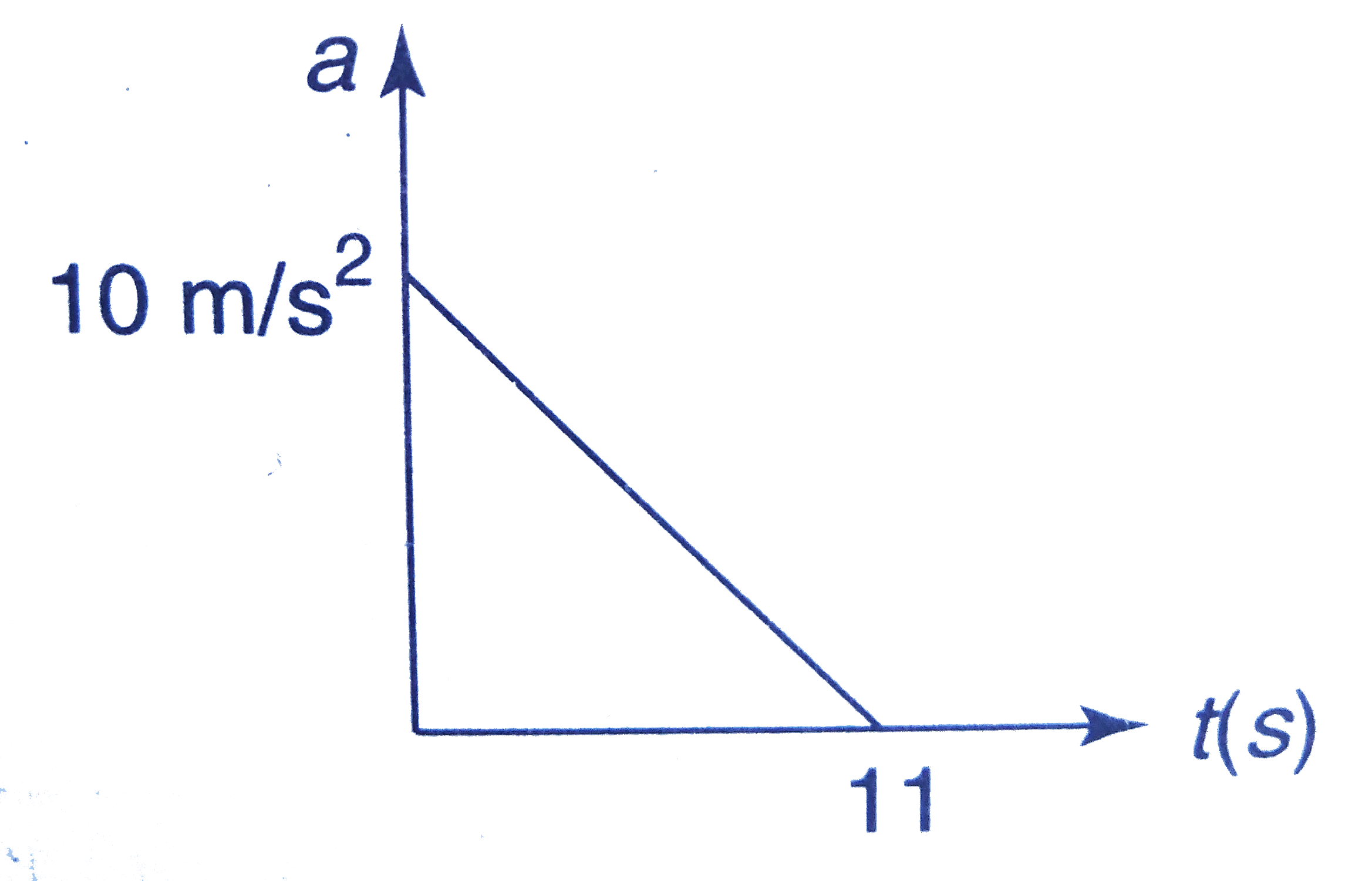
View SolutionA particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.
View SolutionThe velocity - displacement graph of a particle moving along a straight line is shown
The most suitable acceleration - displacement graph will be

View SolutionConsider a disc rotating in the horizontal plane with a constant angular speed `omega` about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed `(1)/(8)` rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then
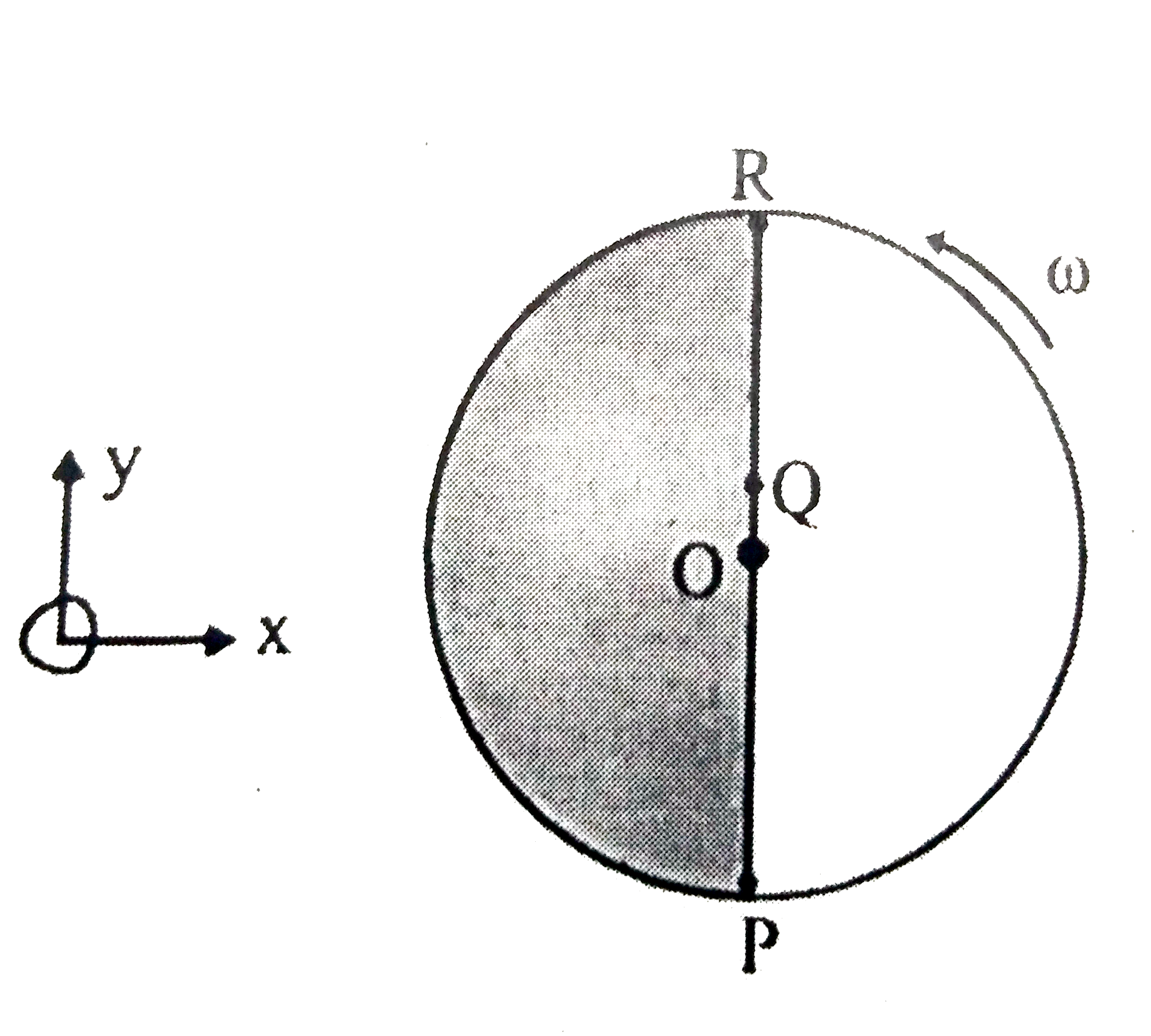
View Solution
Single Correct Answer Type questions and complete solutions for chapter MISCELLANEOUS KINEMATICS of CENGAGE PHYSICS (HINGLISH) of Class 11