Complete Solutions to COMPREHENSION_TYPE of chapter KINEMATICS 1 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS 1 |
| DC PANDEY MASTER PROBLEM PACKAGE | COMPREHENSION_TYPE |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
A particle starts from rest with a time varying acceleration `a=(2t-4)`. Here `t` is in second and `a` in `m//s^(2)`
Particle comes to rest after a time `t=`………… second
View SolutionA particle starts from rest with a time varying acceleration `a=(2t-4)`. Here `t` is in second and `a` in `m//s^(2)`
Maximum velocity of particle in negative direction is at `t=`…………… second
View SolutionA particle starts from rest with a time varying acceleration `a=(2t-4)`. Here `t` is in second and `a` in `m//s^(2)`
The velocity time graph of the particle is
View Solution`x` and `y` co-ordinates of a particle moving in `x-y` plane at some instant of time are `x=2t` and `y=4t`.Here `x` and `y` are in metre and `t` in second. Then
The distance travelled by the particle in a time from `t=0` to `t=2s` is ………`m`
View Solution`x` and `y` co-ordinates of a particle moving in `x-y` plane at some instant of time are `x=2t` and `y=4t`.Here `x` and `y` are in metre and `t` in second. Then
The path of the particle is a…….
View SolutionAt time `t=0`, particle `A` is at `(1m,2m)` and `B` is at `(5m,5m)`. Velociyt of `B` is `(2hati+4hatj)m//s` Velocity of particle `A` is `sqrt(2)v)` at `45^(@)` with `x`-axis. A collides with `B` .
Value of `v` is ………..m/s
View SolutionAt time `t=0`, particle `A` is at `(1m,2m)` and `B` is at `(5m,5m)`. Velocity of `B` is `(2hati+4hatj)m//s` Velocity of particle `A` is `sqrt(2)v)` at `45^(@)` with `x`-axis. A collides with `B` .
Time when `A` will collide with `B` is …….second.
View SolutionThe position of a particle is given by
`x=2(t-t^(2))`
where `t` is expressed in seconds and `x` is in metre.
The acceleration of the particle is
View SolutionThe position of a particle is given by
`x=2(t-t^(2))`
where `t` is expressed in seconds and `x` is in metre.
The maximum value of position co-ordinate of particle on positive `x`-axis is
View SolutionThe position of a particle is given by
`x=2(t-t^(2))`
where `t` is expressed in seconds and `x` is in metre.
The particle
View SolutionThe position of a particle is given by
`x=2(t-t^(2))`
where `t` is expressed in seconds and `x` is in metre.
The total distance travelled by the paticle between `t=0` to `t=1s` is
View SolutionThe position of a particle is given by
`x=2(t-t^(2))`
where `t` is expressed in seconds and `x` is in metre.
When does the object return to its initial velocity?
View SolutionThe position of a particle is given by
`x=2(t-t^(2))`
where `t` is expressed in seconds and `x` is in metre.
When is the object at rest?
View SolutionThe graph given shows the positions of two cars, `A and B`, as a function of time. The cars move along the x-axis on parallel but separate tracks, so that they can pass each other's position without colliding. At which instant in time is car-A overtaking the car-B ?
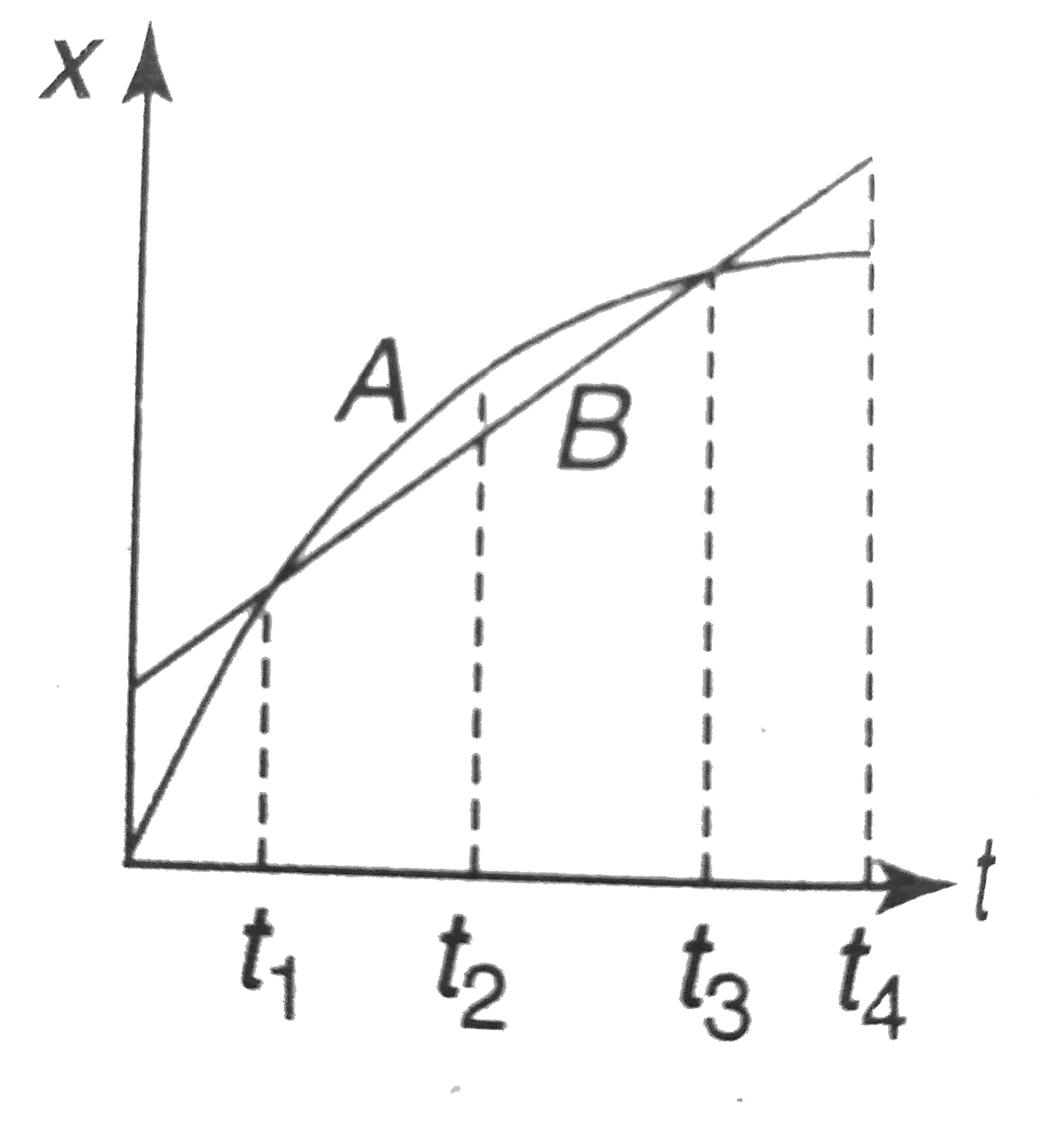
View SolutionThe graph given show the position of two cars `A` and `B` as a function of time. The cars move along the `x` axis on parallel but separate tracks, so that they can pass each other's position without colliding.

At time `t_(3)` which car is moving faster?
View SolutionThe graph given shows the positions of two cars, `A and B`, as a function of time. The cars move along the x-axis on parallel but separate tracks, so that they can pass each other's position without colliding. At which instant in time is car-A overtaking the car-B ?

View SolutionThe graph given show the position of two cars `A` and `B` as a function of time. The cars move along the `x` axis on parallel but separate tracks, so that they can pass each other's position without colliding.

Which one of the following best describes the motion of car `A` as shown on the graphs?
View SolutionTwo trains `R` and `S` are approaching each other on a straight track, the former with a uniform velocity of `25m//s` and the latter with `15m//s`. When the are `225m` apart brakes are siultaneously applied to both of them. The deceleration given by te brakes to the train `S` increases linearly with time by `0.3m//s^(2)` every second (i.e. `dv//dt=-0.3t`), while the train `R` is given a uniform deceleration
What must be the minimum deceleration of train `R` so that the trains do not collide?
View SolutionTwo trains A and B are approaching each other on a straight track, the former with a uniform velocity of 25 m/s and other with 15m/s, when they are 225 m a part brakes are simultaneously applied to both of them. The deceleration given by the brakes to thetrain B increases linearly with time by `0.3 m//s^(2)` every second, while the train A is given a uniform deceleration, (a) What must be the minimum deceleration of the train A so that the trains do not collide ? (b) What is the time taken by the trains to come to stop ?
View Solution
COMPREHENSION_TYPE questions and complete solutions for chapter KINEMATICS 1 of DC PANDEY ENGLISH of Class 11