Complete Solutions to MCQ_TYPE of chapter KINEMATICS 1 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS 1 |
| DC PANDEY MASTER PROBLEM PACKAGE | MCQ_TYPE |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
Velocity displacement graph of a particle moving in a straight line is as shown in figure.
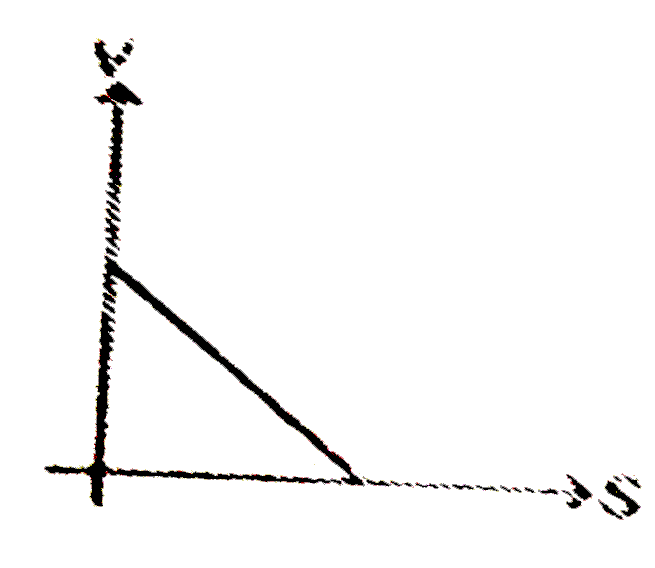
View SolutionLet `v` and `a` be the instantaneous velocity and acceleration of a particle moving in a plane. Then rate of change of speed `(dv)/(dt)` of the particle is equal to
View SolutionStarting from rest a particle is first accelerated for time `t_1` with constant acceleration `a_1` and then stops in time `t_2` with constant retardation `a_2.` Let `v_1` be the average velocity in this case and `s_1` the total displacement. In the second case it is accelerating for the same time `t_1` with constant acceleration `2a_1` and come to rest with constant retardation `a_2` in time `t_3.` If `v_2` is the average velocity in this case and `s_2` the total displacement, then
View SolutionA particle leaves the origin with an initial velodty `v= (3.00 hati) m//s` and a constant acceleration `a= (-1.00 hati-0.500 hatj) m//s^2.` When the particle reaches its maximum x coordinate, what are
(a) its velocity and (b) its position vector?
View SolutionAcceleration of a particle which is at rest at ` x=0 ` is `vec a = (4 -2 x) hat i`. Select the correct alternative (s).
View SolutionA car is moving rectilinearly on a horizontal path with acceleration `a_(0)`.A person sitting inside the car observes that an insect `S` is crawling up the screen with an acceleration a.If `theta` is the inclination of the wind screen with the horizontal, then the acceleration of the insect.
View SolutionThe coordinate of a particle moving in a plane are given by ` x(t) = a cos (pt) and y(t) = b sin (pt)` where `a,b (lt a)` and `P` are positive constants of appropriate dimensions . Then
View SolutionA particle moving along a straight line with uniform acceleration has velocities `7 m//s` at A and `17 m//s` at C. B is the mid point of AC. Then :-
View SolutionLet `r` be the radius vector of a particle in motion about some reference point and `r` its modulus. Similarly, `v` be the velocity vector and `v` its modulus. Then
View SolutionTwo particles `A` and `B` are located in `x-y` plane at points `(0,0)` and `(0,4m)`. They simultaneoulsy start moving with velocities `v_(A)=2hatjm//s` and `v_(B)=2hatim//s`. Select the correct alternative(s)
View SolutionThe co-ordinate of the particle in x-y plane are given as `x=2+2t+4t^(2)` and `y=4t+8t^(2)` :-
The motion of the particle is :-
View SolutionRiver is flowing with a velocity `v_(BR)=4hatim//s`. A boat is moving with a velocity of `v_(BR)=(-2hati+4hatj)m//s` relative to river. The width of the river is `100m` along `y`-direction. Choose the correct alternative(s)
View SolutionA particle is moving along `x`-axis. Its velocity `v` with `x` co-ordinate is varying as `v=sqrt(x)`. Then
View SolutionFrom `v-t` graph shown in figure. We can draw the following conclusions
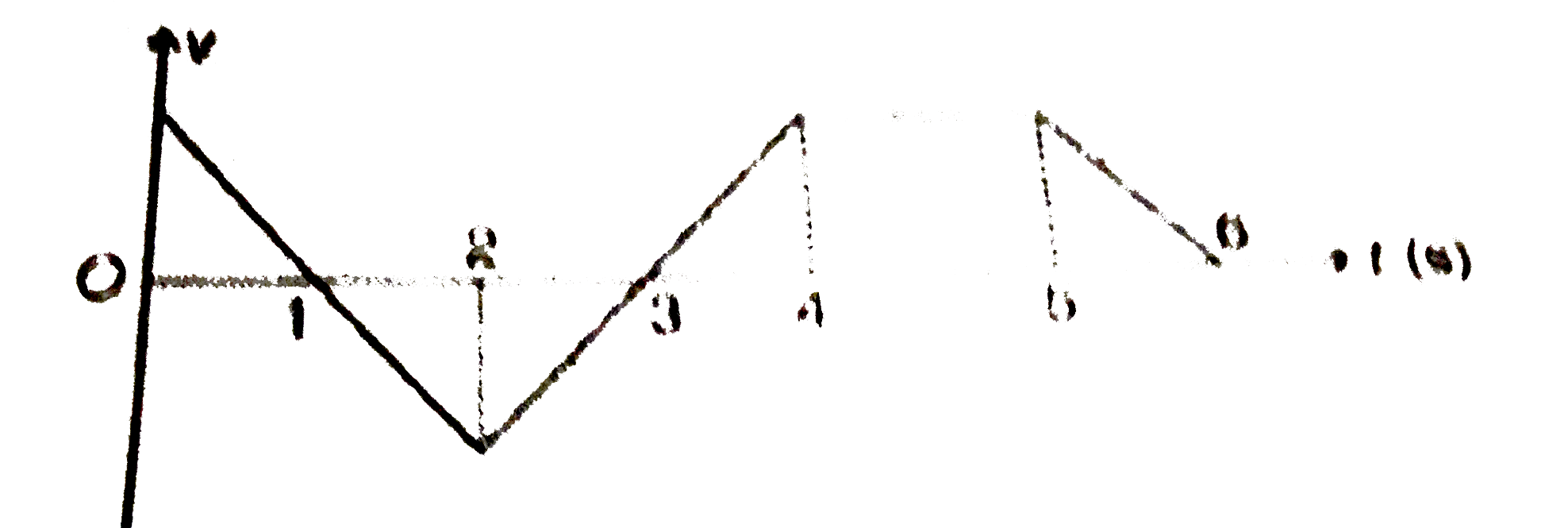
View SolutionA particle `P` is projected upwards with `80m//s`. One second later another particle `Q` is projected with initial velocity `70m//s`. Before either of the particle srikes the ground `(g=10m//s^(2))`
View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
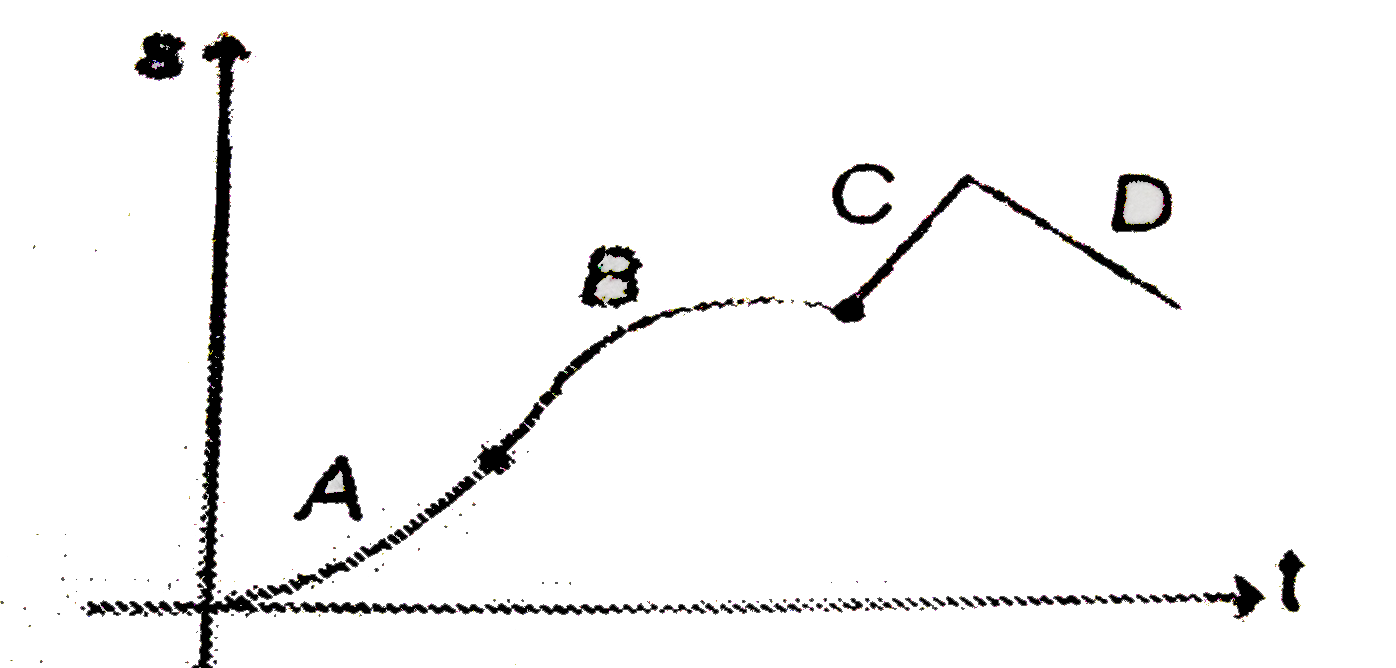
View SolutionAt time `t=0`, a particle is at `(-1m, 2m)` and at `t=2s` it is at `(-4m,6m)`. From this we can conclude that in the given time interval.
View SolutionA particle `P` lying on a smooth horizontal `x-y` plane starts from `(3hati+4hatj)m` with velocity `(2hati)m//s`. Another particle `Q` is projected (horizontally from origin with velocity `(xhati+yhatj)` so that is strikes `P` after `2s`. Then
View SolutionPath of a particle moving in `x-y` plane is `y=3x+4`. At some instant suppose `x`- component of velocity is `1m//s` and it is increasing at a constant rate of `1m//s^(2)`. Then at this instant.
View SolutionA particle moves along the X-axis as `x=u(t-2s)=at(t-2)^2`.
View SolutionA man standing on the edge of the terrace of a high rise building throws a stone, vertically up with at speed of `20 m//s`. Two seconds later, an identical stone is thrown vertically downwards with the same speed of `20 m`,. Then
View SolutionThe `v-t` graph for two particles `P` and `Q` are given in the figure. Consider the following statements(s). Then, which of the following statement(s) is/are True:

View SolutionA particle is moving in a straight line along the positive `x`-axis such that its speed is inversely proportional to the distance from origin `[vprop1/x impliesv=k/x` where `k` is the proportionally constant].
The graph of motion of the particle for `1//v` versus `x` (distance from origin) is shown in the figure.
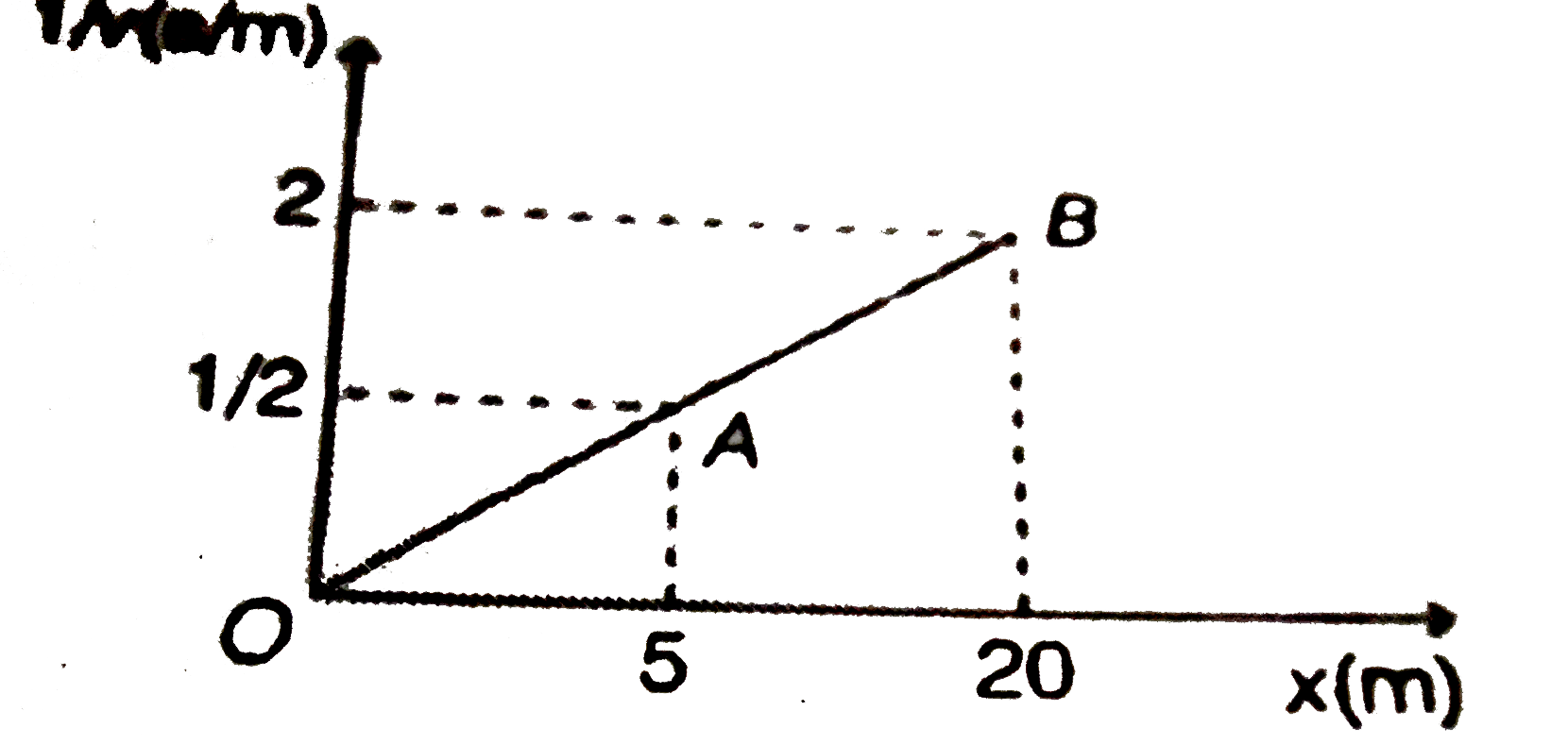
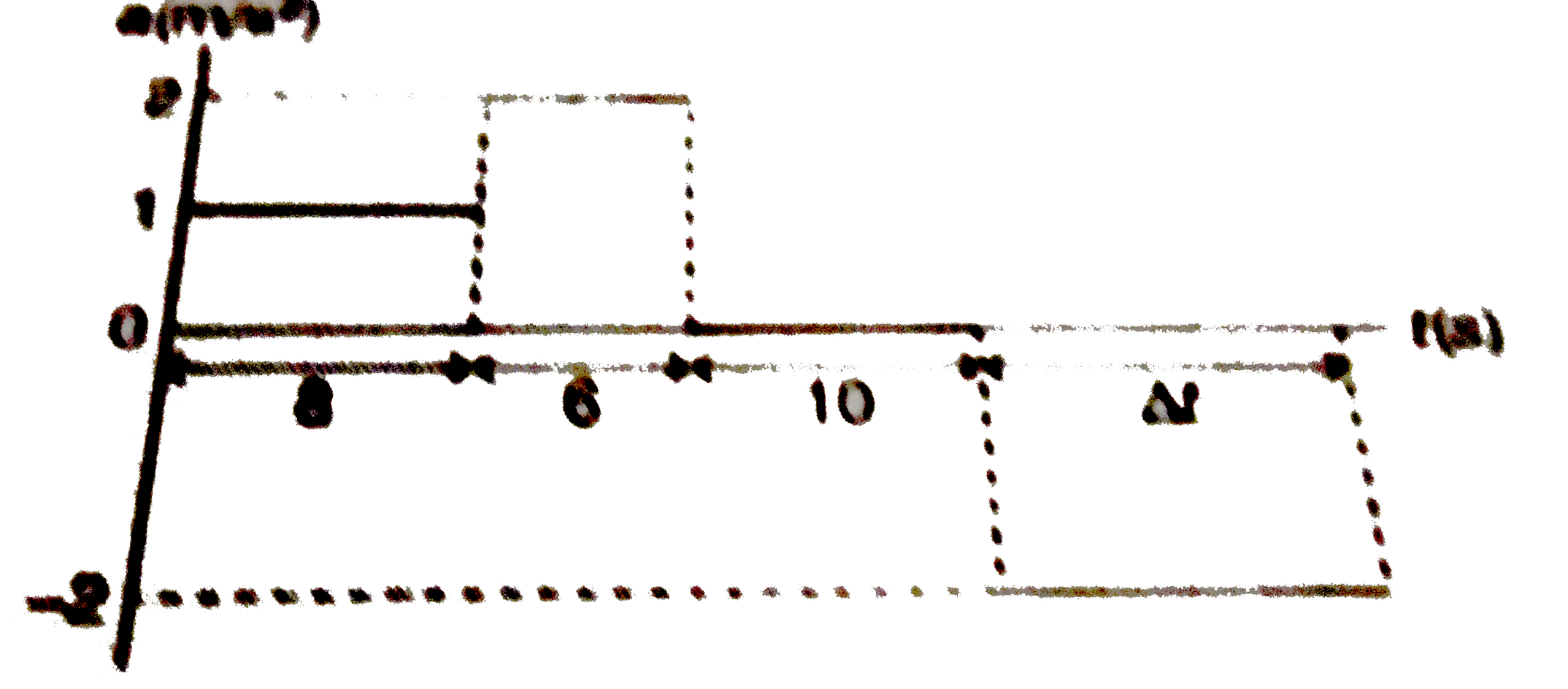
View SolutionA subway train travels between two of its stations at then stops with the acceleration shcedule shown in the acceleration versus time graph. Then
View SolutionA particle starts moving with initial velocity `3m//s` along `x`- axis from origin. Its acceleration is varying with `x` co-ordinate in parobalic nature as shown in the figure. At `x=1m `, tangent to the graph makes an angle `45^(@)` with positive `x`- aixs. Then at `x=3m`,
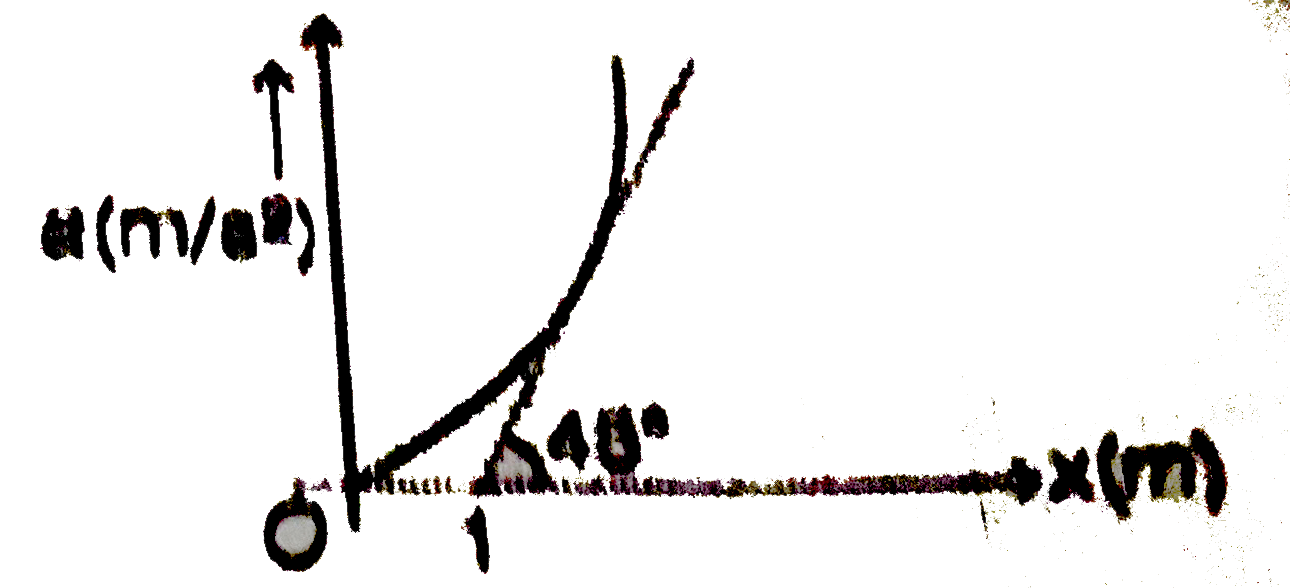
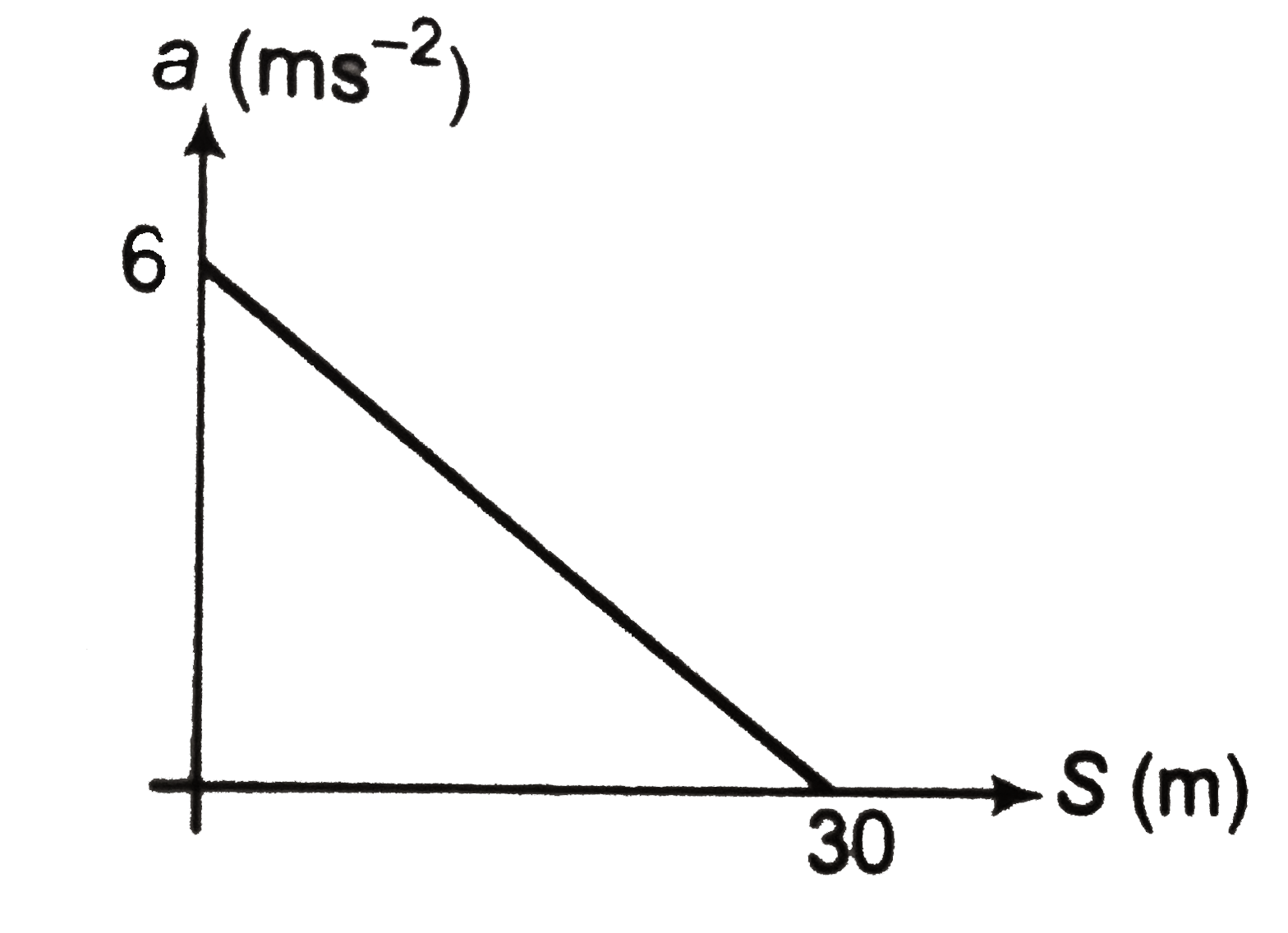
View SolutionA train starts from rest at `S = 0` and is subjected to an acceleration as shown in figure. Then,
View SolutionMan A is sitting in a car moving with a speed of 54 `(km)/(hr)` observes a man B in front of the car crossing perpendicularly a road of width 15 m in three seconds. Then the velocity of man B (in `(m)/(s)`) will be:
View Solution
MCQ_TYPE questions and complete solutions for chapter KINEMATICS 1 of DC PANDEY ENGLISH of Class 11