Complete Solutions to SCQ_TYPE of chapter KINEMATICS 1 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS 1 |
| DC PANDEY MASTER PROBLEM PACKAGE | SCQ_TYPE |
| Number Of Questions | 87 |
| Academic Year | 2023-24 |
A particle has a velocity u towards east at `t=0`. Its acceleration is towards west and is constant. Let `x_A` and `x_B` be the magnitude of displacements in the first 10 seconds and the next 10 seconds
View SolutionA body starts from rest and is uniformly accelerated for `30` s. The distance travelled in the first `10` s is `x_(1)`, next `10` s is `x_(2)` and the last `10` s is `x_(3)`. Then `x_(1):x_(2):x_(3)` is the same as :-
View SolutionA ball is dropped from the top of a building. The ball takes `0.5s` to fall the `3m` length of a window some distance from the to of the building. If the speed of the ball at the top and at the bottom of the window are `v_(T)` and `v_(T)` respectively, then `(g=9.8m//s^(2))`
View SolutionA ball is dropped into a well in which the water level is at a depth `h` below the top. If the speed of sound is `C`, then the time after which the splash is heard will be give by.
View SolutionTwo identical balls are shot upward one after another at an interval of 2s along the same vertical line with same initial velocity of `40 ms^-1`. The height at which the balls collide is
View SolutionA stone thrown upwards with a speed u from the the top of the tower reaches the ground with a speed 3u. The height of the tower is
View SolutionA body iniitially at rest is moving with uniform acceleration a. Its velocity after n seconds is v. The displacement of the body in last 2 s is
View SolutionA balloon is moving upwards with velocity `10m//s`. It releases a stone which comes down to the ground in `11s`. The height of the balloon from the ground at the moment when the stone was dropped is `(g=10m//s^(2))`
View SolutionA particle is thrown upwards from ground. It experiences a constant resistance force which can produce a retardation of `2 ms^-2.` The ratio of time of ascent to time of descent 13 (`g = 10 ms^-2`)
View SolutionShown in the figure are the velocity time graphs of the two particle `P_(1)` and `P_(2)` moving in same straight line in same direction. Which of the following statements about their relative motion is true?
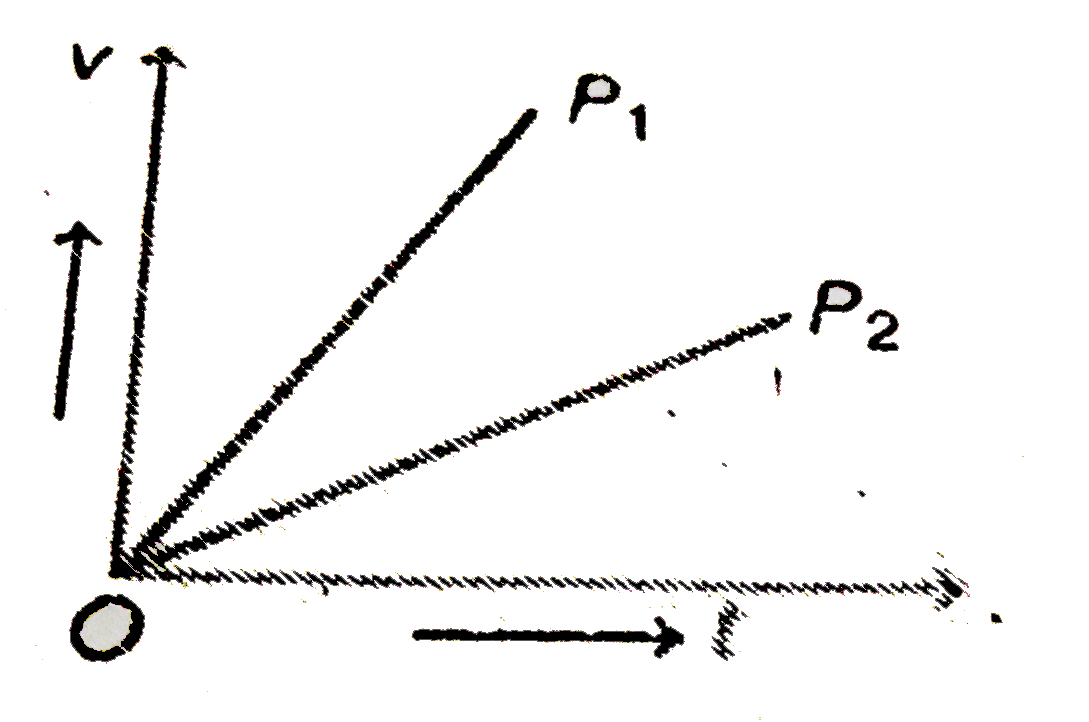
Their relative velocity
View SolutionTwo trains `A` and `B` `, 100km` apart are travelling towards each other on different tracks with same starting speed of `50km//h`. The train `A` accelerates at `20km//h^(2)` and the train `B` retards at the rate `20km//h^(2)`. The distance covered by the train `A` when they cross each other is
View SolutionTo cross the river in shortest distance, a swimmer should swimming an angle ` theta` with the upsteram. What is the ratio of the time taken to swim across in the shortest time to that in swimming across over shortest distance. [Asume that the speed of swimmer in still water is greater than the speed of river flow]
View SolutionRaindrops are falling vertically with a velocity `10 m//s`. To a cyclist moving on a straight road the rain drops appear to be coming with a velocity of `20m//s`. The velocity of cyclist is :-
View SolutionAt a metro station, a girl walks up a stationary escalator in time `t_1`. If she remains stationary on the escalator, then the escalator take her up in time `t_2`. The time taken by her to walk up on the moving escalator will be
View SolutionTwo cars are moving in the same direction with a speed of 30 km/h. They are separated from each direction meets the two cars after an interval of 4 minutes, The speed of the third car is
View SolutionA bus is moving with a velocity `10 ms^-1` on a straight road. A scooterist wishes to overtake the bus in `100 s`. If the bus is at a distance of `1 km` from the scooterist, with what velocity should the scooterist chase the bus ?
View SolutionTwo trains take `3s` to pass another when going in the opposite directions but only `2.5s` if the speed of one is increased by `50%`. The time one would take to pass the other when going in the same direction at their original speed is
View SolutionFor four particle A,B,C,D, the velocities of one with respect to other are given as `vecV_(DC)` is `20(m)/(s)` towards north, `vecV_(BC)` is `20(m)/(s)` towards east and `vecV_(BA)` is `20(m)/(s)` towards south. Then `vecV_(DA)` is
View SolutionA ball is thrown vertically down with velocity of `5m//s`. With what velocity should another ball be thrown down after 2 seconds so that it can hit the `1^(st)` ball in next 2 second.
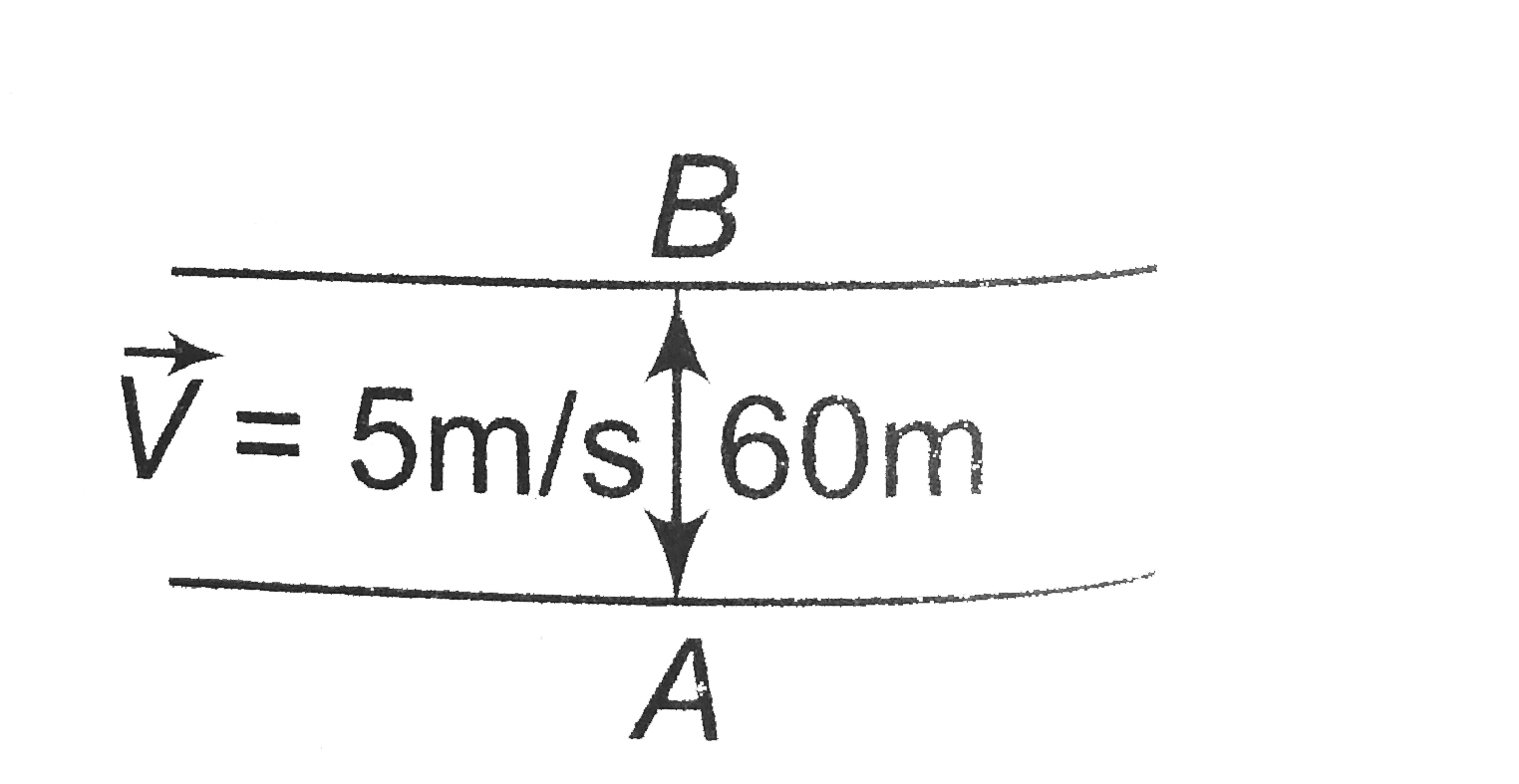
View SolutionA man is crossing a river flowing with velocity of `5m//s`. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be
View SolutionThe velocity of an object moving rectilinearly is given as a function of time by `v=4t-3t^(2)` where `v` is in m/s and `t` is in seconds. The average velocity if particle between `t=0` to `t=2` seconds is
View SolutionThe acceleration-time graph of a particle moving in a straight line is as shown in figure. The velocity of the particle at time `t = 0` is `2 m//s`. The velocity after `2` seconds will be

View SolutionTwo cars `A` and `B` cross a point `P` with velocities `10m//s` and `15m//s`. After that they move with different uniform accelerations and the car `A` overtakes `B` with a speed of `25ms^(-1)`. What is velocity of `B` at that instant?
View SolutionThe last soldier of an `80m` long marching troops runs from the end to its front, and then it runs back to the end with the same speed. During this, the marching troop covers a distance of `150m`. The distance covered by the soldier is
View SolutionIf position time graph of particle is sine curve as shown, what will be its velocity-time graph.

View SolutionThe greatest acceleration or deceleration that a train may have is a. The minimum time in which the train may reach form one station to the other seprated by a distance d is-
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity `u` in first `t` seconds is.
View SolutionDuring a accelerated motion of a particle
View SolutionTwo particles are released from the same height at an interval of `1s`. How long aftger the first particle begins to fall will the two particles be `10m` apart? (`g=10m//s^(2)`)
View SolutionA body travelling along a straight line , one thired of the total distance with a velocity ` 4 ms^(-1)`. The remaining part of the distance was covered with a velocity ` 2 ms^(-1)` for half the time and with velocity ` 6 ms^(-1)` for the other half of time . What is the mean velocity averaged over te whle time of motin ?
View SolutionTwo cars start off to race with velocities `4 m/s and 2 m/s` and travel in straight line with uniform accelerations `1 msec^-2`and 2 msec − 2` respectively. If they reach the final point at the same instant, then the length of the path is.
View SolutionA juggler maintains four balls in motion, making each to them to rise a height of `20 m` from his hand. What time interval should he maintain, for the alphaer distance between them.
View SolutionThe displacement of a particle moving in a straight line is described by the relation `s=6+12t-2t^(2)`. Here `s` is in metre and `t` in second. The distance covered by the particle in first `5s` is
View SolutionA ball projected upwards from the foot of a tower. The ball crosses the top of the tower twice after an interval of `6 s` and the ball reaches the ground after `12 s`. The height of the tower is `(g = 10 m//s^2)` :
View SolutionA particle is projected vertically upwards from a point A on the ground. It takes time to reach a point B, but it still continues to move up. If it takes further time to reach the ground from point B. Then height of point B from the ground is :
View SolutionA particle is released from rest from a tower of height 3h. The ratio of time intervals for fall of equal height h i.e. `t_(1):t_(2):t_(3)` is :
View SolutionA ball is dropped from the roof of a tower height `h`. The total distance covered by it in the last second of its motion is equal to the distance covered by it in first three seconds. The value of `h` in metre is `(g=10m//s^(2))`
View SolutionBall `A` is dropped from the top of a building. At the same instant ball `B` is thrown vertically upwards from the ground. When the balls collide, they are moving in opposite direction and the speed of `A` is twice the speed of `B`. At what fraction of the height of the building did the collision occurs ?
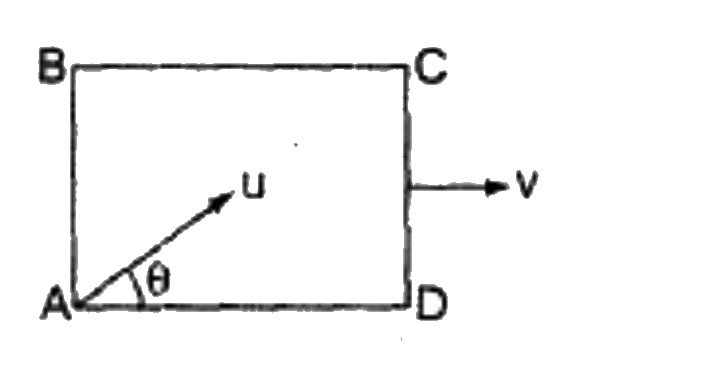
View SolutionA horizontal smooth square platform ABCD is moving towards the right with a uniform speed v. At what angle `theta` must a particle slide from A, on the platform, with speed u so that it strikes the point B?
(Assume u to be uniform and `u gt v`)
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff with initial speed `v and 2 v`. The relative position of the second stone with respect to first varies with time till both the stones strike the ground as.
View SolutionOne stone is dropped from a tower from rest and simultaneously another stone is projected vertically upwards from the tower with some initial velocity. The graph of distance (s) between the two stones varies with time (t) as (before either stone hits the ground).
View SolutionA particle is dropped from point `A` at a certain height from ground. It falls freely and passes through thre points `B, C` and `D` with `BC=CD`. The time taken by the particle to move from `B` to `CD` is `2s` and from `C` to `D` is `1s`. The time taken to move from `A` to `B` is s
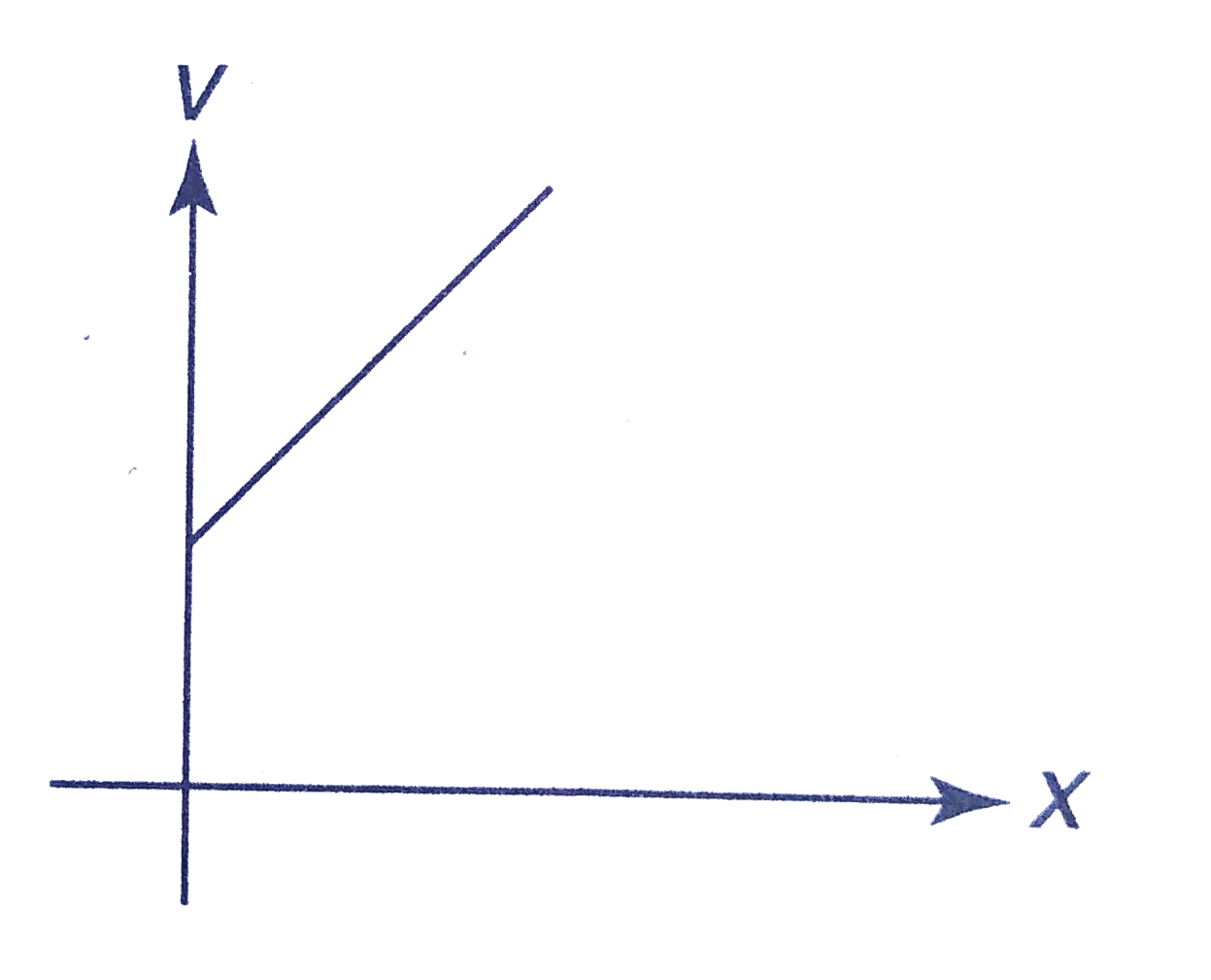
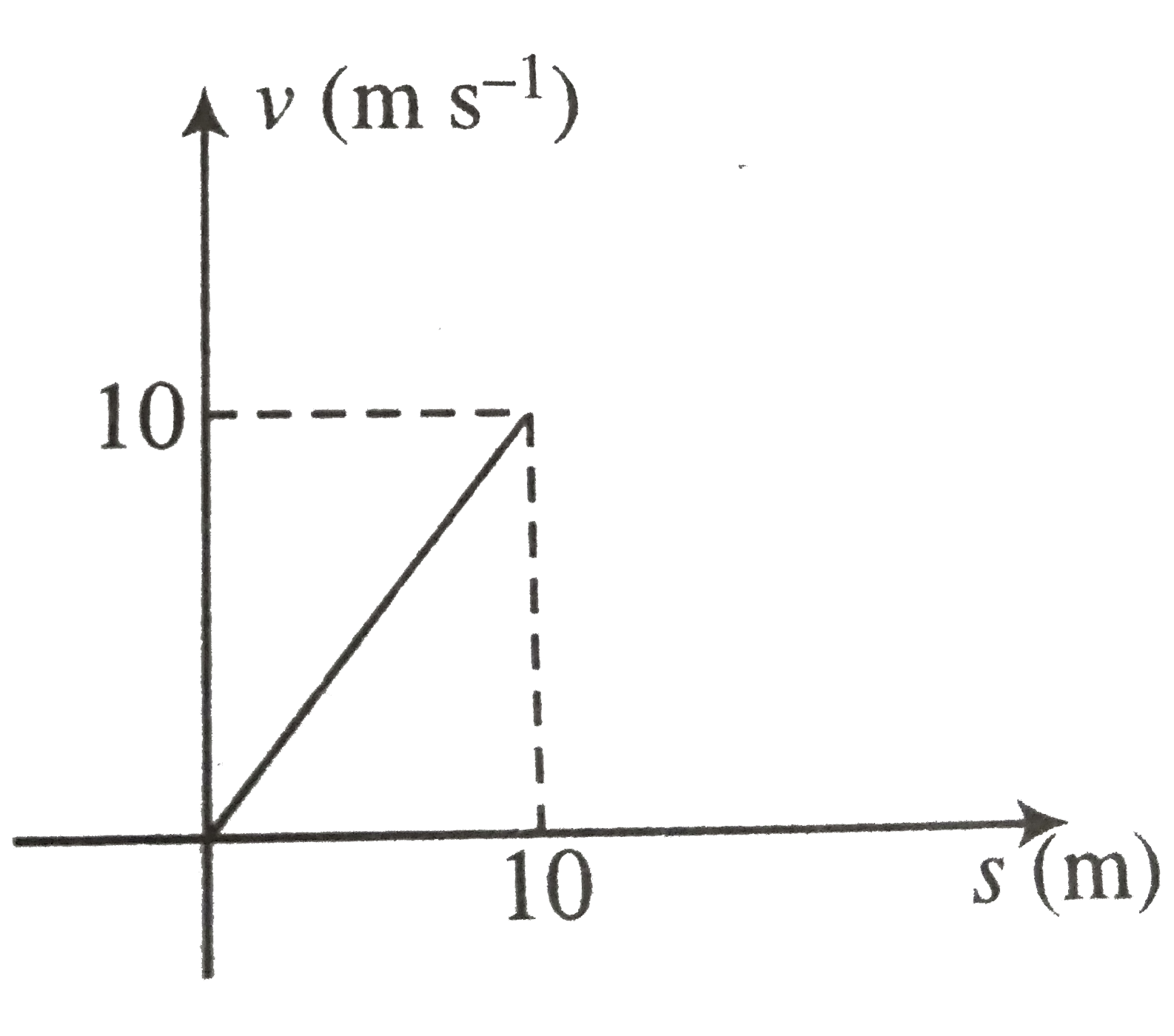
View SolutionGraph of velocity versus displacement of a particle moving in a straight line is as shown in figure.
The acceleration of the particle is.
View SolutionA ball is dropped from a certain height on a horizontal floor. The coefficient of restitution between the ball and the floor is `(1)/(2)`. The displacement time graph of the ball will be.
View SolutionThe speed -time graph of the ball in the above situation is.
View SolutionVelocity time equation of a particle moving in a straight line is `v=2t-4` for `tle2s` and `v=4-2t` for `tgt2`.The distance travelled by the particle in the time interval from `t=0` to `t=4s ` is (Here `t` is in second and `v` in m/s)
View SolutionA body starts from the origin and moves along the X-axis such that the velocity at any instant is given by `(4t^3-2t)`, where t is in sec and velocity in m/s. what is the acceleration of the particle when it is 2 m from the origin?
View SolutionTwo objects are moving along the same straight line. They cross a point A With an acceleration a, 2a and velocity 2u, u at time `t = 0.` The distance moved by the object when one overtakes the
View SolutionTwo balloons are moving in air with velocities `v_(1)={2thati+(t-2)hatj)m//s` and `v_(2)={(t-4)hati+thatj}m//s` then at what `t` balloons are moving parallel to each other:
View SolutionVeolocity-time graph of a particle undergoing rectilinear motioin is plotted upto `t=t_(4)` as shown in the figure. Average acceleration of the particle is zero in the time internal between
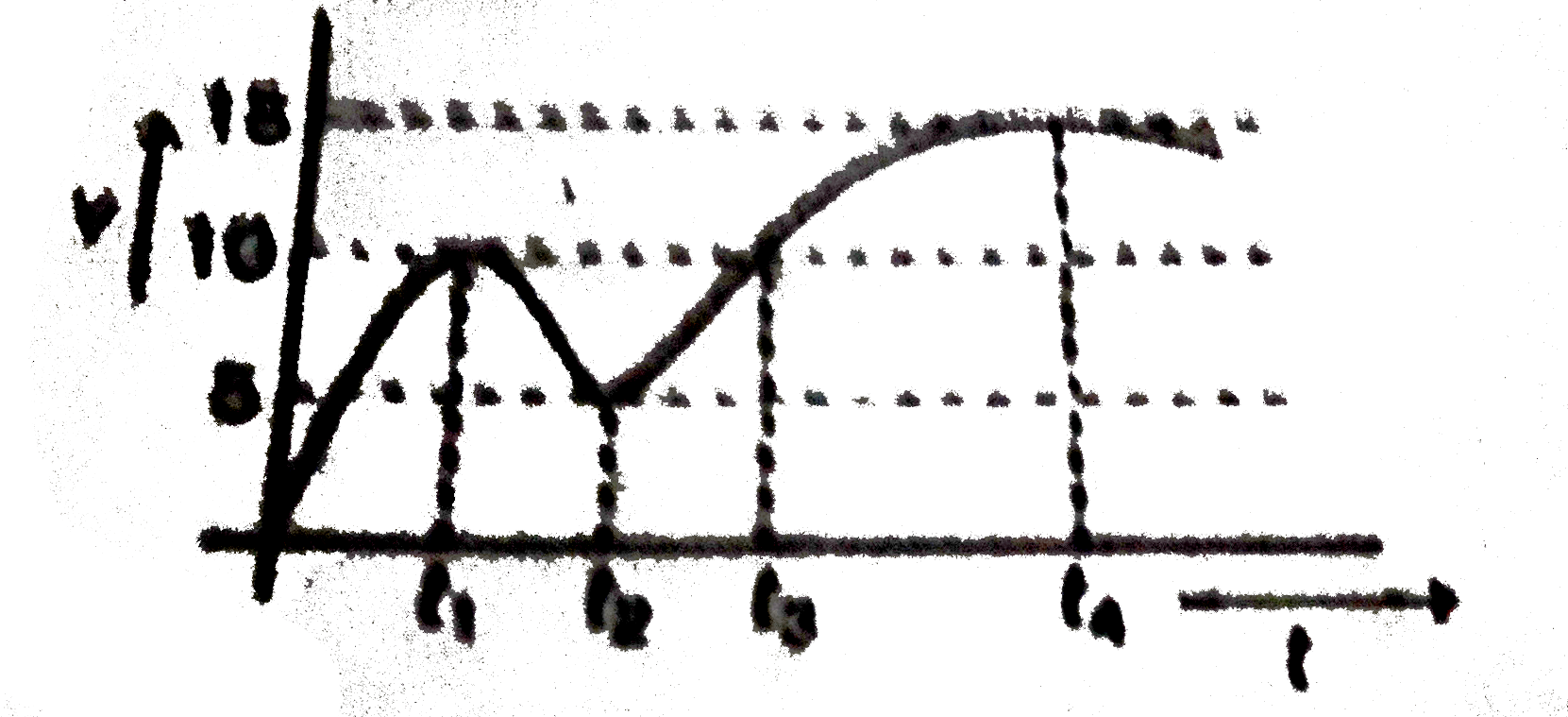
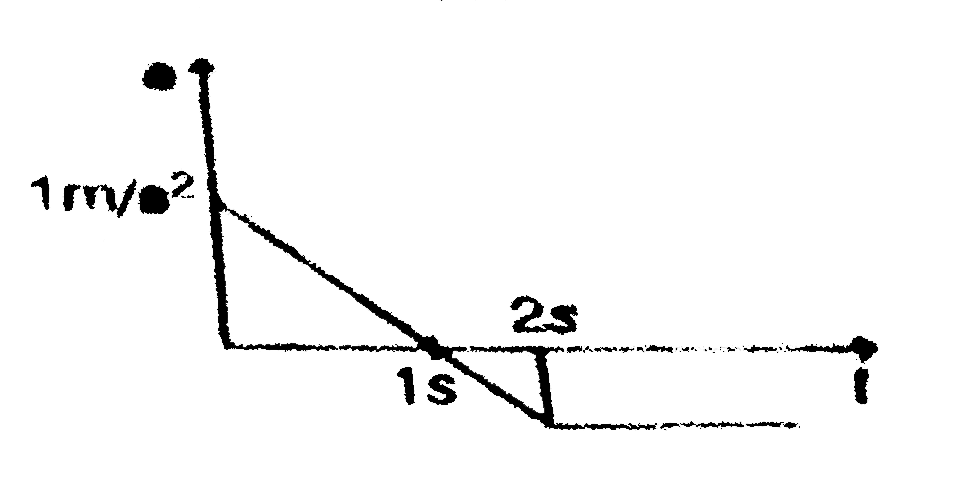
View SolutionAcceleration versus time curve for a particle moving in a straight line is shown in the figure. If particle starts from rest at `t=0`, then which of the following curve is correct for the same particle.
View SolutionAn airplane flies northward from town `A` and `B` and then back again. There is a steady wind blowing towards the north so that for the first state of the trip, the airplane is flying in the same direction as the wind and for the return trip of the journey, the airplane is flying opposite of the wind. The total trip time `T_(omega)` as compared to the total trip time in the absence of any winds `T_(0)` is:
View SolutionA car breaks a traffic signal with a speed of `40m//s`. After `2s`, a policeman starts following him with a constant acceleration of `12.5m//s^(2)`. Taking the position of signal to be origin, correct position time graph would be
View SolutionA plane is flying at a speed of `720kmh^(-1)` with respect to air. The wind is blowing at a speed of `54kmh^(-1)` from west to east. With respect to ground the plane is found to be movig northwards. In which direction is the plane heading?
View SolutionA particle is moving on a straight line. Its velocity at time `t` is `(8-2t)m//s`. What is the total distance covered from `t=0` to `t=6s`?
View SolutionA ball is dropped from a tower of height `h` under gravity. If it takes `4s` to reach the ground from height `h/2`, then time taken by it to reach from `h` to `h/2` is nearly:
View SolutionVelocity of a particle varies with time as `v=athati+2ht^(2)hatj`. If the particle starts from point `(0,c)`, the trajectory of the particle is
View SolutionTwo particles start moving from the same point along the same straight line. The first moves with constant velocity `v` and the second with constant acceleration `a`. During the time that elapses before the sound catches the first, the greatest distance between the particle is.
View SolutionA glass wind screen whose inclination with the vertical can be changed is mounted on a car. The moves horizontally with a speed of `2m//s`. At what angle `alpha` with the vertical should the wind screen placed so that the rain drops falling vertically downwards with velcoity `6m//s` strike the wind screen perpendicularly?
View SolutionA swimmer crosses a flowing stream of width `omega` to and fro in time `t_(1)`. The time taken to cover the same distance up and down the stream is `t_(2)`. If `t_(3)` is the time the swimmer would take to swim a distance `2omega` in still water, then
View SolutionA point mass starts moving in straight line with constant acceleration `a` from rest at `t=0`. At time `t=2s`, the acceleration changes the sign remaining the same in magnitude. The mass returns to the initial position at time `t=t_(0)` after start of motion. Here `t_(0)` is
View SolutionIn a car race car `A` takes `t_(0)` time less to finish than car `B` and pases the finishing point with a velocity `v_(0)` more than car `B`. The cars start from rest and travel with constant accelerations `a_(1)` and `a_(2)` . Then the ratio `(v_(0))/(t_(0))` is equal to
View SolutionA particle moves in space along the path `z=ax^(3)+by^(2)` in such a way that `(dx)/(dt)=c=(dy)/(dt)` where `a,b` and `c` are constants. The acceleration of the particle is
View SolutionFour rods of side length `l` have been hinged to form a rhombus. Vertex `A` is fixed to a rigid support, vertex `C` is being moved along the `x`-axis with constant velocity `V` as shown in figure. The rate at which vertex `B` is nearing the `x`-axis at the moment the rhombus is in the form of a squarem is
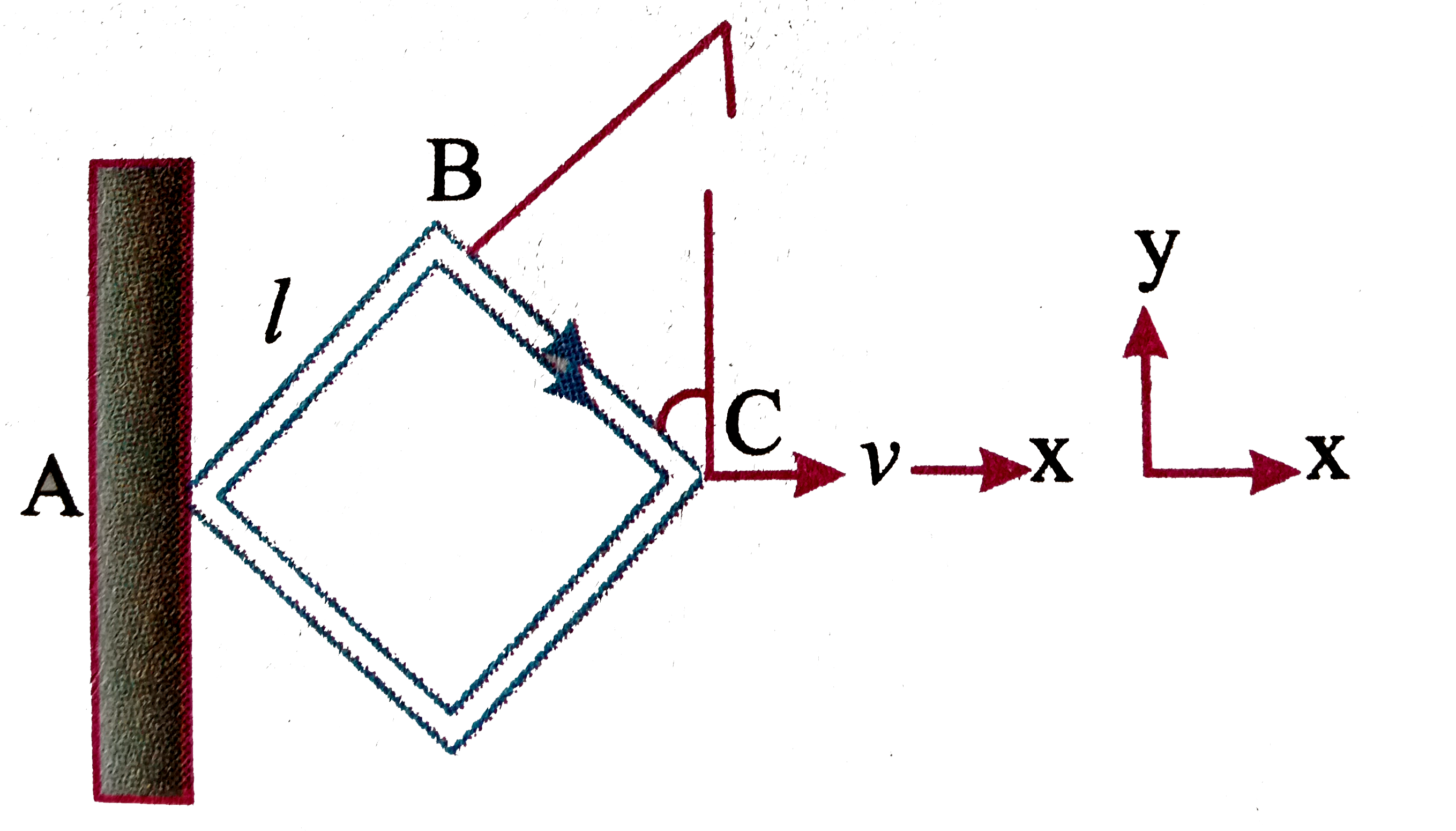
View SolutionA car leaves station `X` for station `Y` every 10 min. The distance between `X` and `Y` is `60km`. The car travels at speed `60km//h`. A man drives a car from `Y` towards `X` at speed `60km//h`. If he starts at the moment when first car leaves station `X`, how many cars would he meet om route?
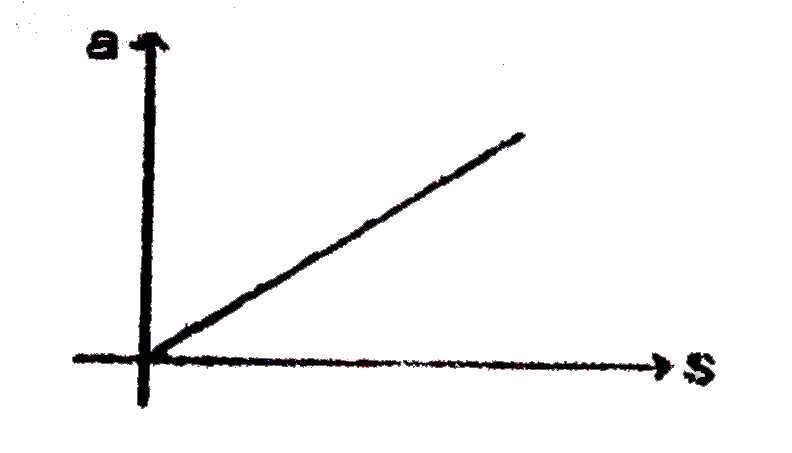
View SolutionAcceleration `(a)` -displacement `(s)` graph of a particle moving in a straight line is as shown in the figure. The initial velocity of the particle is zero. The `v-s` graph of the particle would be
View SolutionA horizontal wid is blowing with a velocity `v` towards north-east. A man starts running towards north with acceleration `a`. The after which man will feel the wind blowing towards east is
View SolutionThe distance between two moving particles `P` and `Q` at any time is a.If `v_(r)` be their relative velocity and if `u` and `v` be the components of `v_(r)`, along and perpendicular to `PQ`.The closest distance between `P` and `Q` and time that elapses before they arrive at their nearest distance is
View SolutionConsider a collection of a large number of particles each with speed v. The direction of velocity is randomly distributed in the collection. Show that the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is greater than v.
View SolutionVelocity versus displacement graph of a particle moving in a straight line as shown in figure.
The corresponding acceleration versus velocity graph will be .
View SolutionA particle is moving in `x-y` plane with `y=x/2` and `V_(x)=4-2t`. The displacement versus time graph of the particle would be
View SolutionA car 2m long and 3m wide is moving at `10m//s` when a bullet hits it in a direction making an angle of `tan^(-1)(3//4)` with the car as seen from the ground. The bullet enters one edge of the car at the corner and passes out at diagonally opposite corner. Neglecting gravity, the time for the bullet to cross the car is
View SolutionA particle starts from rest and moves with an acceleration of `a={2+|t-2|}m//s^(2)` The velocity of the particle at `t=4` sec is
View SolutionA `2-m` wide truck is moving with a uniform speed `v_(0)=8 ms^(-1)` along a straight horizontal road. `A` pedestrian starts to cross the road with a uniform speed `v` when the truck is `4 m` away from him, The minimum value of `v` so that he can cross the road safely is .
View SolutionIn the one-dimensional motion of a particle, the relation between position `x` and time `t` is given by `x^(2)+2x=t` (here `xgt0`). Choose the correct statement
View SolutionA particle moves in `x-y` plane, starting from `A` along straight line path `AB` and `BC` as shown in the graph. When it is at point `P` angle between diections of its average velocity and instantaneous velocity is `[tan37^(@)=3//4]`

View SolutionA particle is moving along `x`-axis with constant acceleration. At `t=0`, the particle is at `x=3m` and `(dx)/(dt)=+4m//s`. The maximum value of `x` co-ordiante of the particle is observed 2 seconds later. Starting from `t=0` sec, after what time, particle reaches its initial position again?
View SolutionThe acceleration of a particle which moves along the positive x-axis varies with its position as shown in figure. If the velocity of the particle is `0.8 ms^(-1)` at x = 0, then velocity of the particle at `x = 1.4 m` is `(in ms^(-1))`.
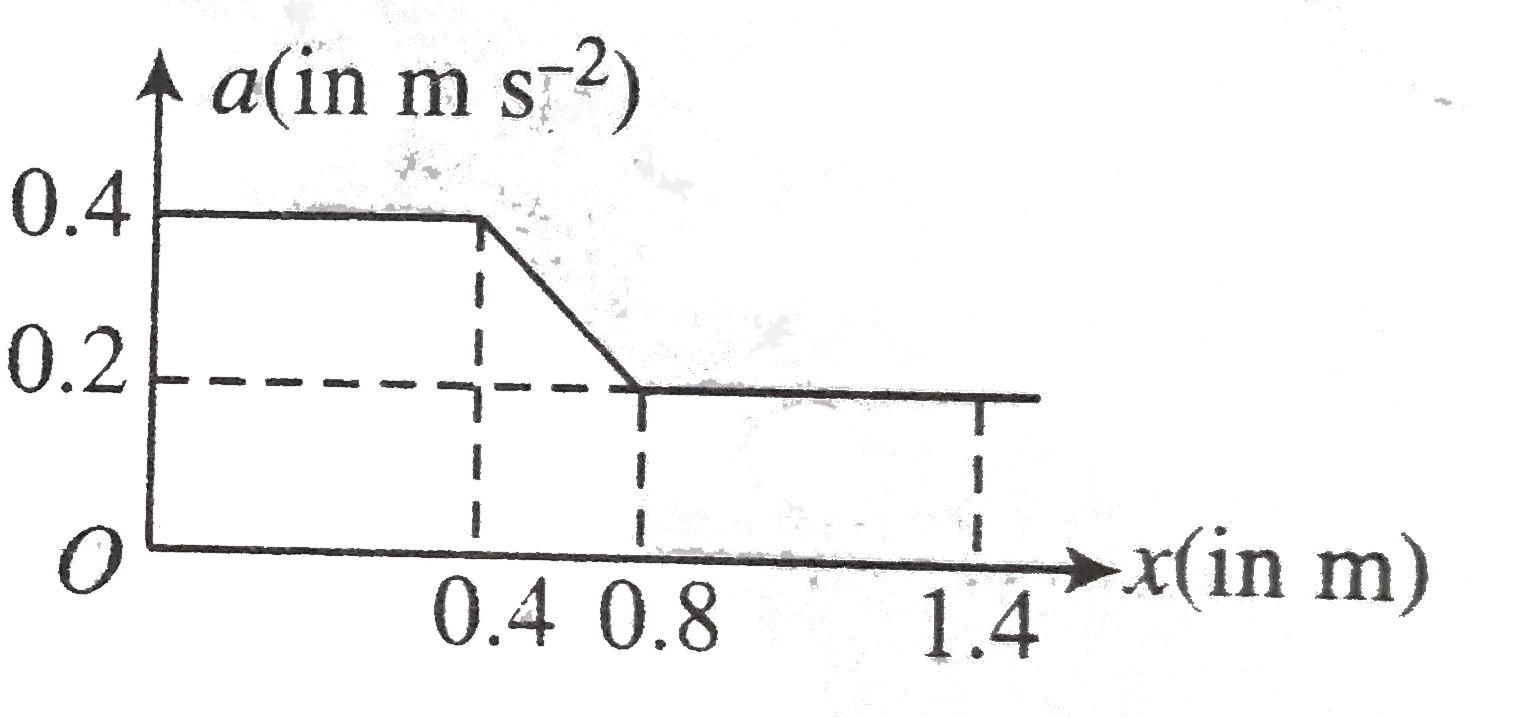
View SolutionA stone is drpped from the top of a tall cliff and n seconds later another stone is thrown vertically downwards with a velocity u. Then the second stone overakes the first, below the top of the cliff at a distance given by
View SolutionA boat `'B'` is moving upstream with velocity `3m//s` with respect to ground. An observer standing on the boat observes that a swimmer `'S'` is crossing the river perpendicular to the direction of motion of the boat. If river flow velocity is `4m//s` and swimmer crosses the river of width `100,m` is `50s`. Then
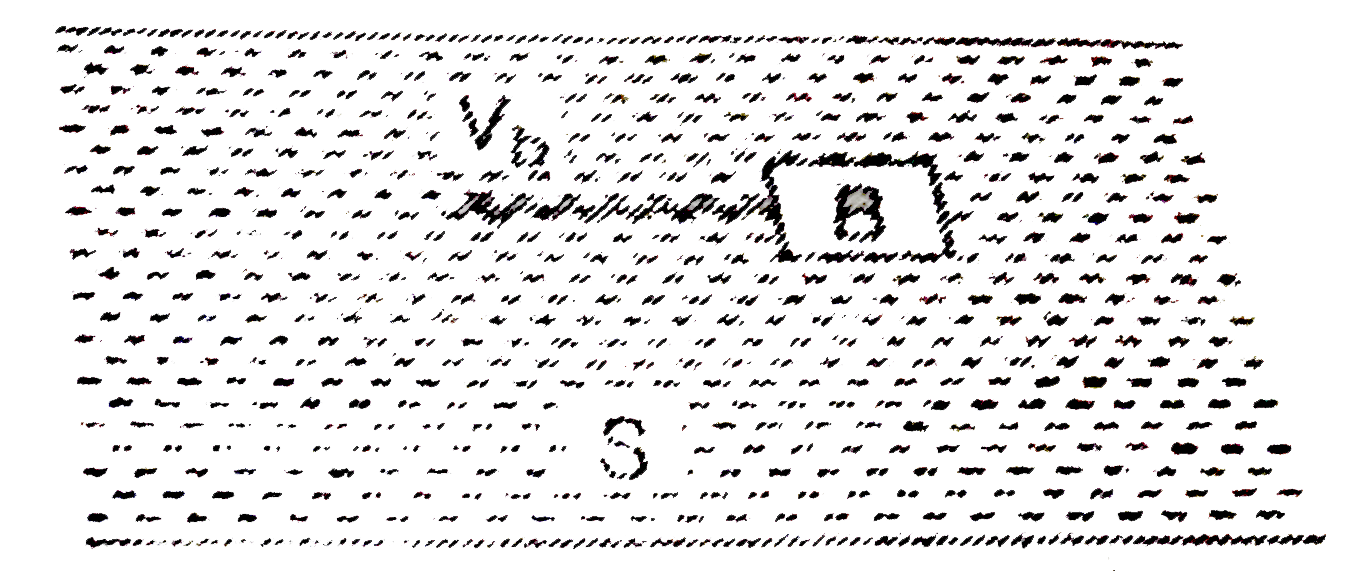
View SolutionA particle moves along the positive `x`-axis with an acceleration`a_(x)` which increases linearly with `x`, as shown in the graph. If the velocity of the particle at `x=4cm` is `0.40m//s` determine the velocity at `x=12cm`
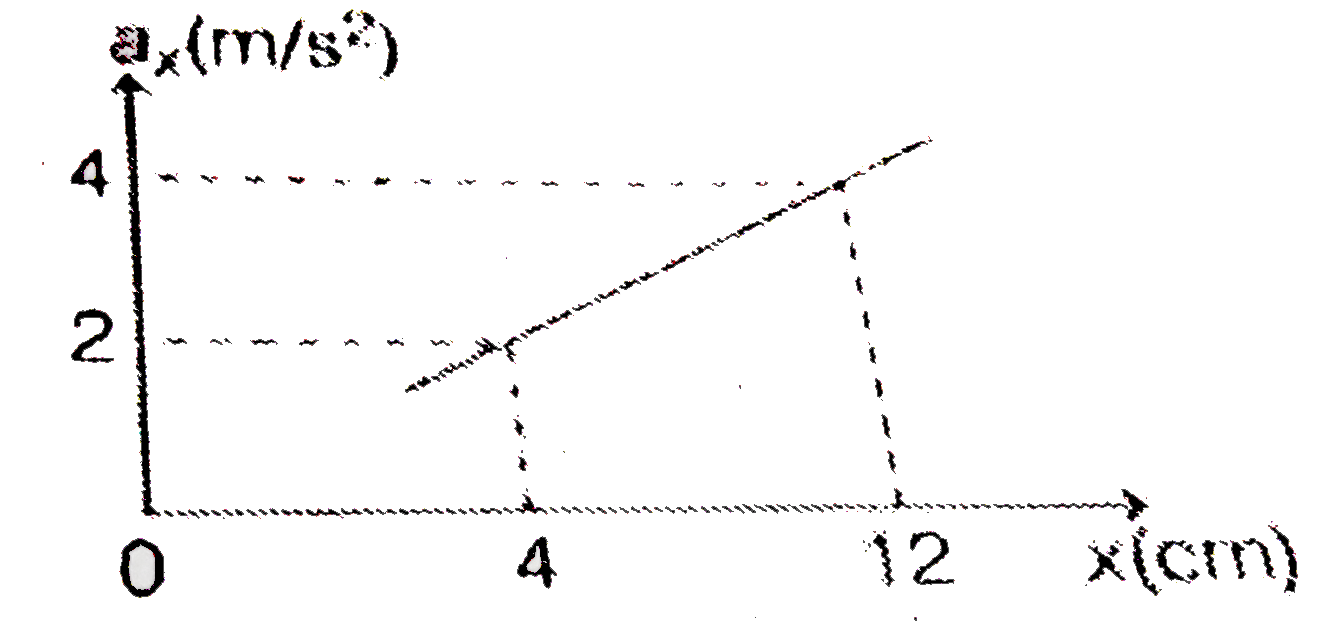
View SolutionIn the figure shown a river of width `4m` is flowing with speed of `5m//s`. A swimmer whose swimming speed relative to the water is `4m/s`, starts swimming from a point `A` on a bank. On the other bank `B` is a point which is directly opposite to `A`. What minimum distance (in m) the swimmer will have to walk on the other bank to reach the point `B`.
View SolutionChoose the correct option:
The string in fig. is passing over small smooth pulley rigidly attached to trolley A. If the speed of trolley is constant and equal to `v_(A)` towards right, speed of block B at the instant shown in figure are
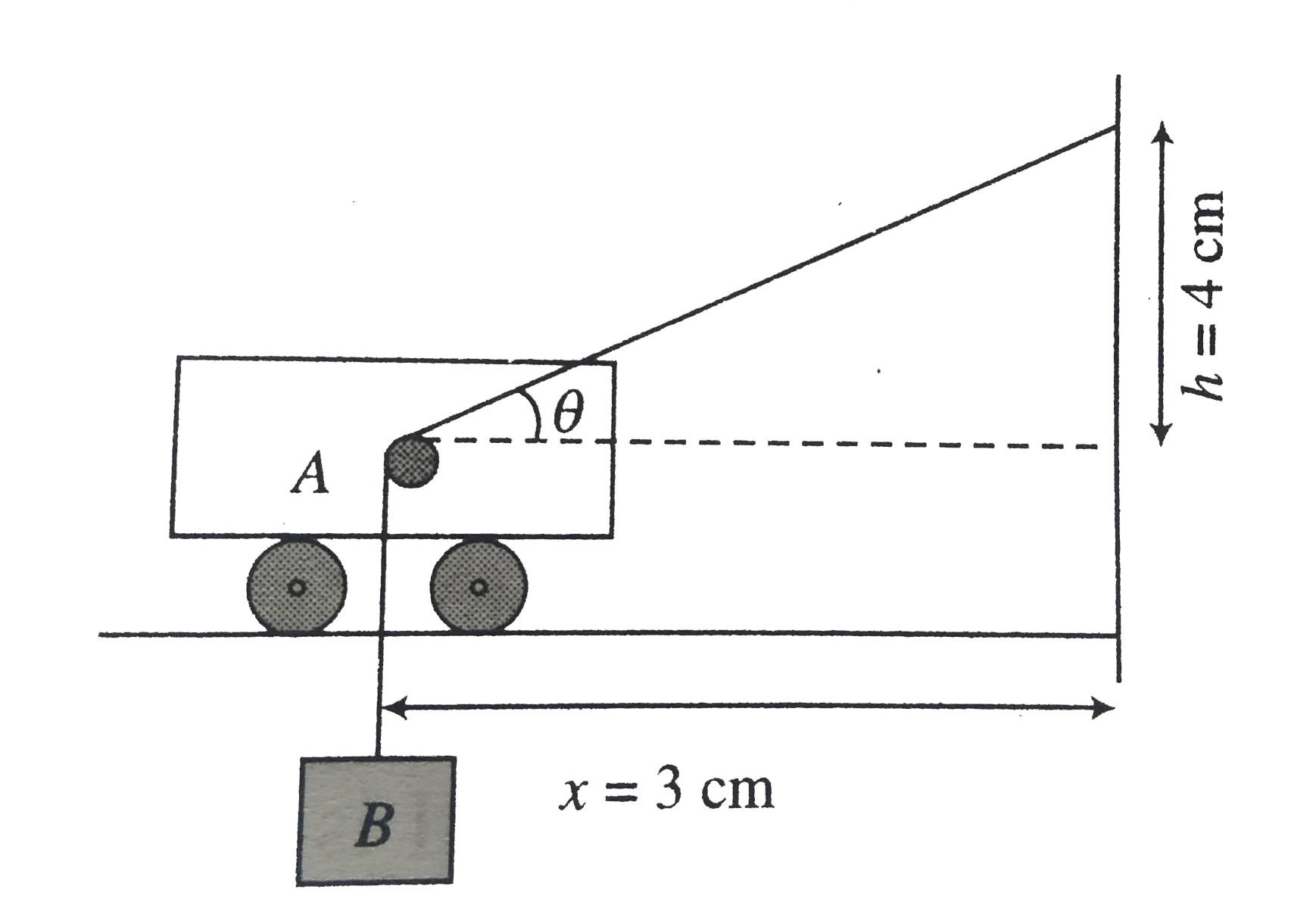
View SolutionA man who swims at a speed of `5km//h` wants to cross a `500m` wide stream flowing at `4km//h` and reach the point which is directly opposite to his starting point. If he reaches a point somewhere else he has to walk back to desitination, his walking speed being `2km//h`. Find the minimum time in which he can reah his destination.

View SolutionTwo particles having position verctors `vecr_(1)=(3hati+5hatj)` metres and `vecr_(2)=(-5hati-3hatj)` metres are moving with velocities `vecv_(1)=(4hati+3hatj)m//s and vecv_(2)=(alphahati+7hatj)m//s`. If they collide after 2 seconds, the value of `alpha` is
View SolutionTwo particles `A` and `B` start from the origin along `x`-axis. Velocity time graph of both particles are shown in the figure. During the given time interval, the maximum separation between the particles is
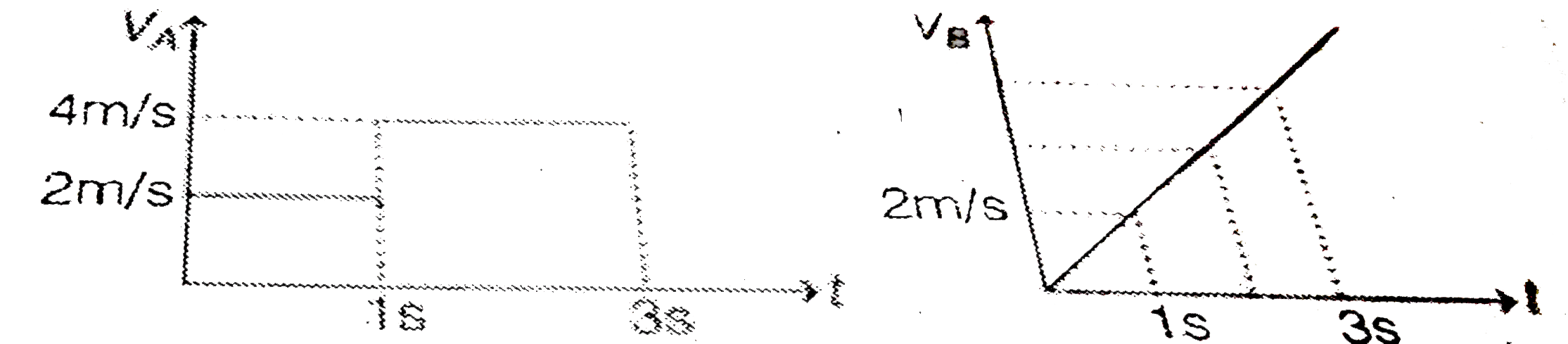
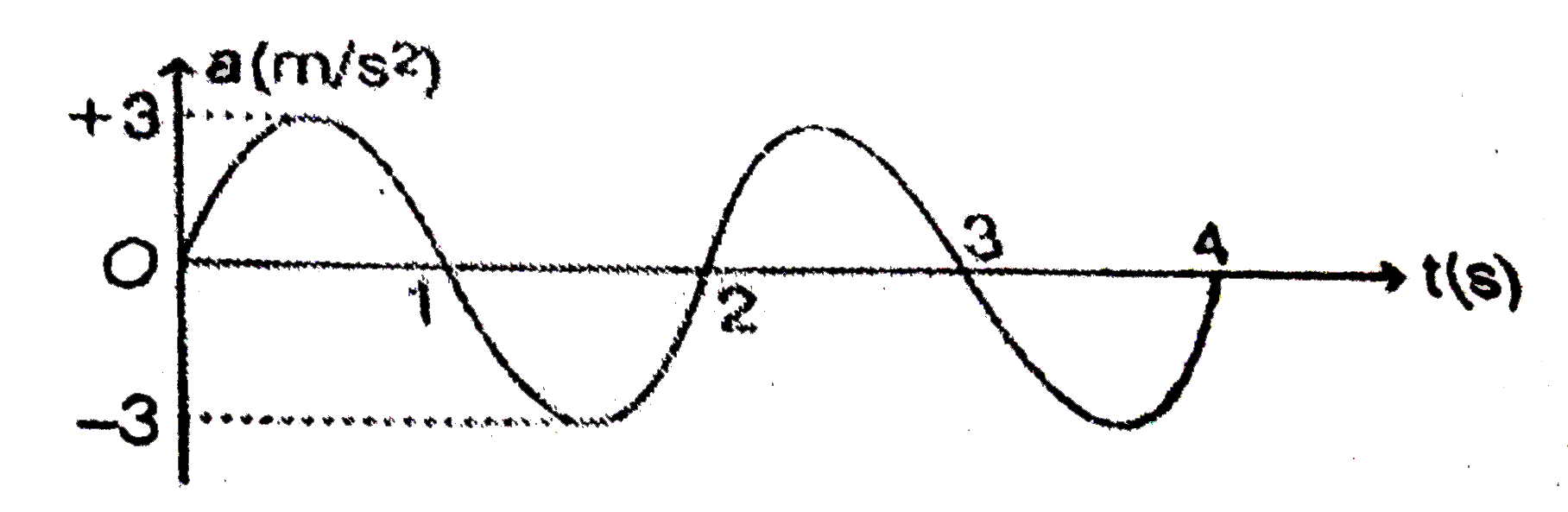
View SolutionA particle is moving in a straight line. Particle was initially at rest. Acceleration versus time graph is shown in figure. Acceleration of particle is given by `a=3sin pi t` in `m//s^(2)`. The time (in s) when the particle comes to rest is
View Solution
SCQ_TYPE questions and complete solutions for chapter KINEMATICS 1 of DC PANDEY ENGLISH of Class 11