Complete Solutions to Example of chapter VECTORS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | Vectors |
| DC PANDEY NEET | Example |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
check Wether the vector `((hati)/sqrt (2)+(hatj)/sqrt(2))` is a unit vector or not .
View SolutionFind the unit vector of `4hati-3hatj+hatk.`
View SolutionIf vector `hati- 3hatj+5hatk and hati-3hatj-ahatk` are equal vector then find the value of a.
View SolutionIf `vec(A) = 3hati +4hatj` and `vec(B) = 7 hat I +24 hatj`, find a vector having the same magnitude as `vec(B)` and parallel to `vec(A)`.
View SolutionTwo forces whose magnitudes are in the ratio `3:5` give a resultant of 28N. If the angle of their inclination is `60^@`, find the magnitude of each force.
View SolutionAboy Walks 4m east and then 3m south .Find the displacement of the boy.
View SolutionIf A=B+C have scalar magnitudes of 5,4,3 units respectively , then find the angle between A and C.
View SolutionFind the sum of vector A and B as shown in the figure ,also find the direction of sum vector. Given A=4unit and B=3 unit .

View SolutionTwo equal vector have a resultant equal to either of them, then the angle between them will be:
View SolutionFind the resultant of three vectors shown in the figure.
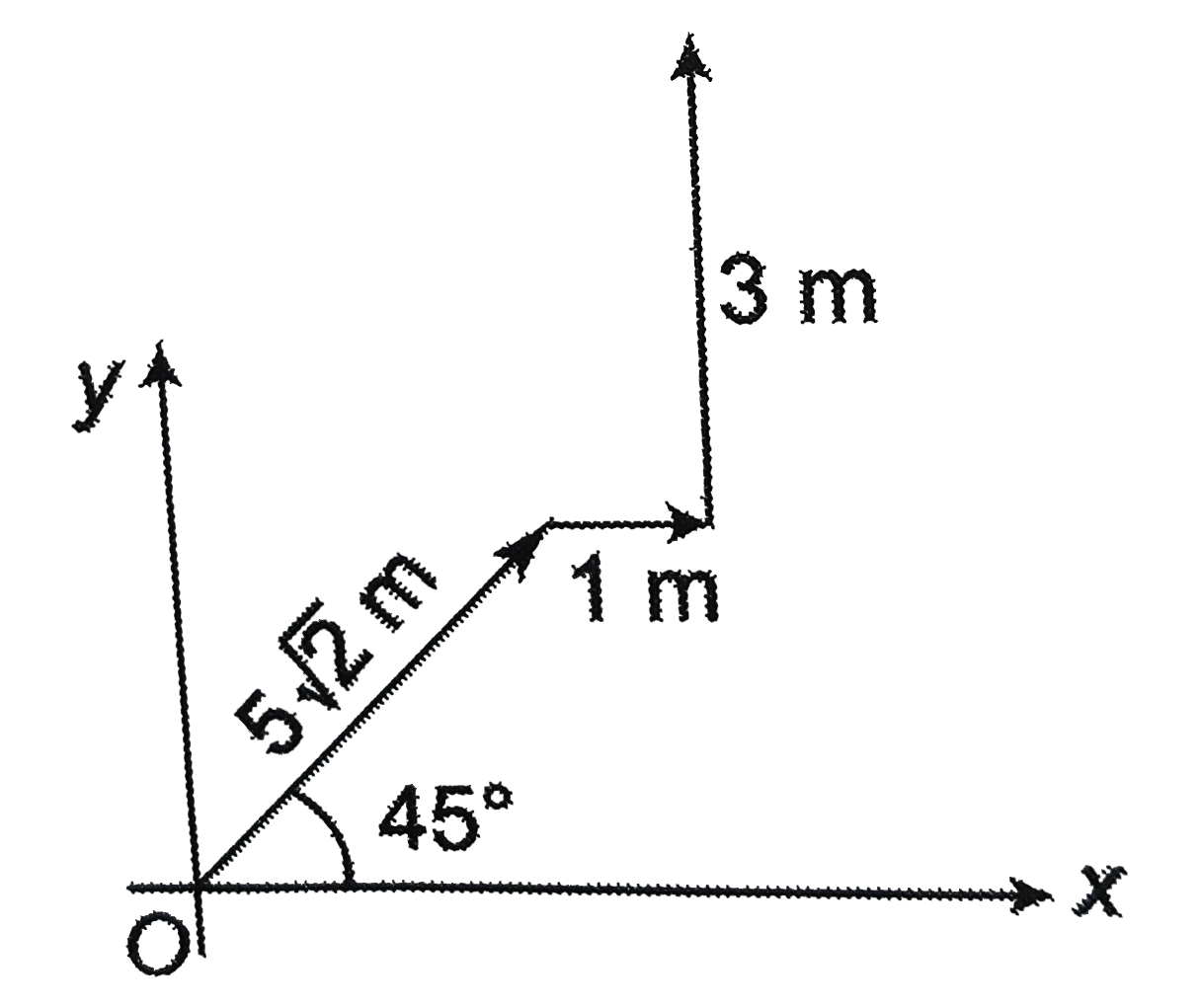
View SolutionFind the subraction of vector A and B as shown in the figure , also find the direction of subtraction vector ,Given A=4 unit and b=3 unit .
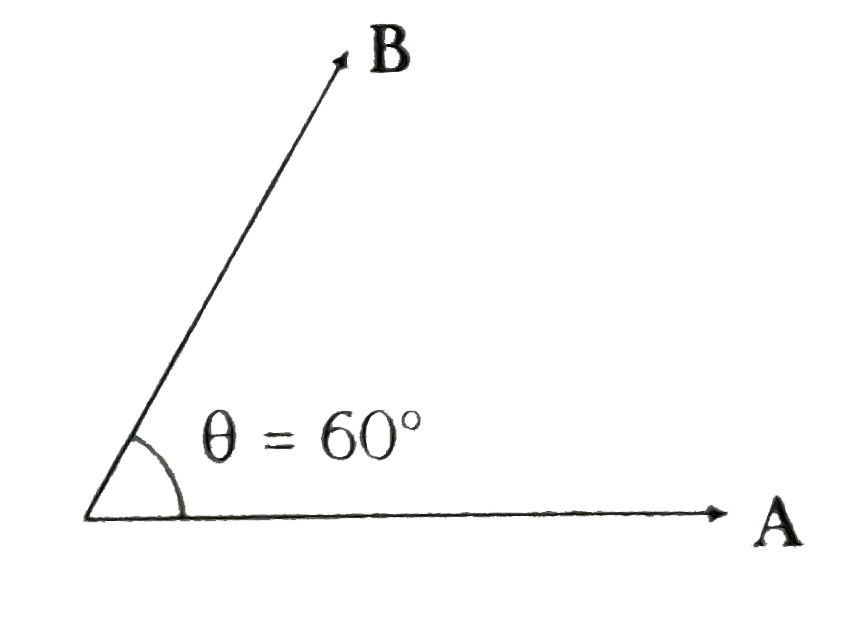
View SolutionObtain the magnitude of 2A - 3B if
`A = hati +hatj- 2 hat k and B = 2 hat i - hat j+hat k` .
View SolutionIf a and b are the vectors AB and BC determined by the adjacent sides of a regular hexagon. What are the vectors determined by the other sides taken is order?
View SolutionThe initial and final position vector for a particle are(-3m) `hati+(2m)hatj+(8m)hatk ` and `(9m)hati+(2m) hatj+(-8m)hatk` respectively ,find the displacement of the particle.
View SolutionIf `|vec(P) + vec(Q)| = |vec(P) - vec(Q)|` , find the angle between `vec(P)` and `vec(Q)`.
View SolutionA vector is given by `vec (A) = 3 hat(i) + 4 hat(j) + 5 hat(k)`. Find the magnitude of `vec(A)` , unit vector along `vec(A)` and angles made by `vec(A)` with coordinate axes.
View SolutionResolve a weight of 10N in two directions which are parallel and perpendiular to a slope inclined at `30^@` to the horizontal.
View SolutionResolve horizontally and vertically a force `F= 8N` which makes an angle of `45^(@)` with the horizontal.
View SolutionFind the resultant of the following forces.
`[sin 37^(@) = (3)/(5) ,cos 37^(@) = (4)/(5) , sin 53^(@) = (4)/(5) , cos 53^(@) = (3)/(5)]`
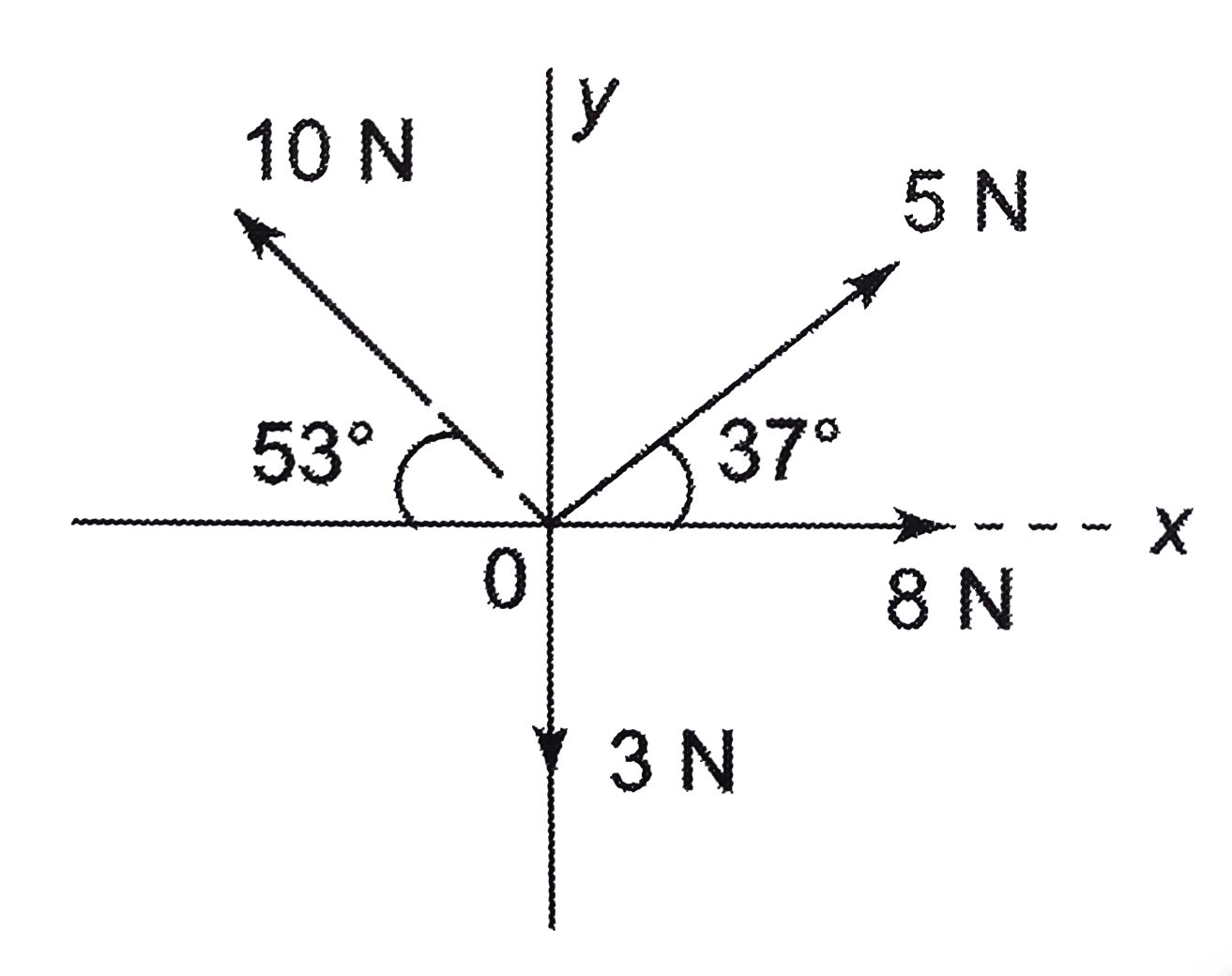
View SolutionFind the angle that the vector `A = 2hati+3hatj-hatk` makes with y-axis.
View SolutionIf a particle moves from the point `A(1 , 2 , 3)` to the point `B( 4 , 6 ,9)`, its displacement vector be
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionFind component of vector A +B along (i) x-axis, (ii) C. Given `A = hati - 2hatj, B=2hati+3hatk` and `C = hati +hatj`.
View SolutionWork done by a force F on a body is W = F .s, where s is the displacement of body. Given that under a force `F = (2 hat i +3 hat j +4 hat k)` N a body is displaced from position vector `r_1 = (2 hat i +3 hat j + hat k)` m to the position vector `r_2 = (hat i +hat j+ hat k)` m. Find the work done by this force.
View SolutionFind the angle between two vector `A=2hati+hatj-hatk andB=hati-hatk.`
View SolutionProve that the vectors `A=2hati-3hatj+hatk and B=hati+hatj + hatk` are mutually perpendicular .
View SolutionFind the (i) Scalar component and (ii)vector component of `A=3hati+4hatj+5hatk on B=hati+hatj+hatk.`
View SolutionShow that the vectors `a =3hati - 2hatj+hatk, b=hati - 3hatj+5hatk` and `c=2hati+hatj-4hatk` form a right angled triangle.
View SolutionProve that the mid-point of the hypotenuse of right angled triangle is equidistant from its vertices.
View SolutionFind the projection of `veca=2hati-hatj+hatk and vecb=hati-2hatj+hatk.`
View SolutionLet a force F be acting on a body free to rotate about a point O and let r the position vector of any point P on the line of action of the force. Then torque `(tau)` of this force about point O is defined as ` tau = rxxF` Given, `F = (2hati + 3hatj - hatk)N and r = (hati- hatj+6hatk)m` Find the torque of this force.
View SolutionFind a unit vector ,`C=AxxB` is a vector perpendicular to both A and B Henc , a unit vector `hatn`perpendicular to A and B can be Written as
`hatn=(C)/(C)=(AxxB)/(|AxxB|)`
`Here, AxxB=|underset(1,-1,1)underset(2,3,1)hati,hatj,hatk|`
`=hati(3+1)+hatj(1-2)+hatk(-2-3)`
`=4hati-hatj-5hatk`
`Further, |AxxB|=sqrt((4)^(2)+(-1)^(2)+(-5)^(2))=sqrt(42)`
`therefore"the desired unit vector is "hatn=(AxxB)/(|AxxB|)`
`or hatn=(1)/(sqrt(42))(4hati -hatj+5hatk)`
View SolutionShow that the vector `A = (hati) - (hatj) + 2 hatk` is parallel to a vector `B = 3hat i - 3hat j + 6hat k`.
View SolutionProve that `|axxb|^2 =a^2b^2 - (a.b)^2`
View SolutionA particle moves on a given straight line with a constant speed v. At a certain time it is at a point P on its straight lline path.O is a fixed point. Show than `vec(OP)xxvec upsilon` is independent of the position P.?
View Solutionif `axxb = bxxc != 0` with a `!= -c` then show that a+c = kb, where k is scalar.
View SolutionLet A,B and C be the unit vectors . Suppose that A.B=A.C =0 and the angle between B and C is `(pi)/(6)` then prove that `A = +-2(BxxC)`
View SolutionThe diagonals of a parallelogram are `2hati` and `2hatj`. What is the area of the parallelogram
View SolutionIf `a=3hati+hatj-4hatk,b=6hati+5hatj-2hatk,` then find the area of a triangle whose adjacent sides are determined by a and b.
View SolutionThe adjacent sides of a parallelogram is given by two vector A and B where `A=5hati-4hatj+3hatkand B=3hati-2hatj+hatk` Calculate the area of parallelogram .
View Solution
Example questions and complete solutions for chapter VECTORS of DC PANDEY ENGLISH of Class 11