Complete Solutions to Subjective of chapter VECTORS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | VECTORS |
| DC PANDEY | Subjective |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
If `a =2hati+3hatj+4hatk and b =4hati+3hatj +2hatk` ,find the angel between a and b.
View SolutionThe vectors `vecA` has a magnitude of 5 unit `vecB` has a magnitude of 6 unit and the cross product of `vecA and vecB` has a magnitude of 15 unit. Find the angle between `vecA and vecB`.
View SolutionSuppose `veca` is a vector of magnitude 4.5 unit due north. What is the vector (a) `3veca` (b) `-4 veca`?
View SolutionTwo vectors have magnitudes 3 unit and 4 unit respectively. What should be the angel between them if the magnitude of the resultant is (a). 1 unit (b). 5 unit and (c). 7 unit.
View SolutionThe work done by a force `vecF` during a displacement `vecr` is given by `vecF.vecr`. Suppose a force of 12 N acts on a particle in vertically upward directionand the particle is displaced through 2.0 m in vertically downward direction. Find the work done by the force during this displacement.
View SolutionIf `vecA,vecB,vecC` are mutually perpendicular show that `vecCxx(vecAxxvecB)=0`. Is the converse true?
View SolutionProve that `vecA.(vecAxxvecB)=0`
View SolutionFind the resultant of the three vectors shown in figure (2W1).
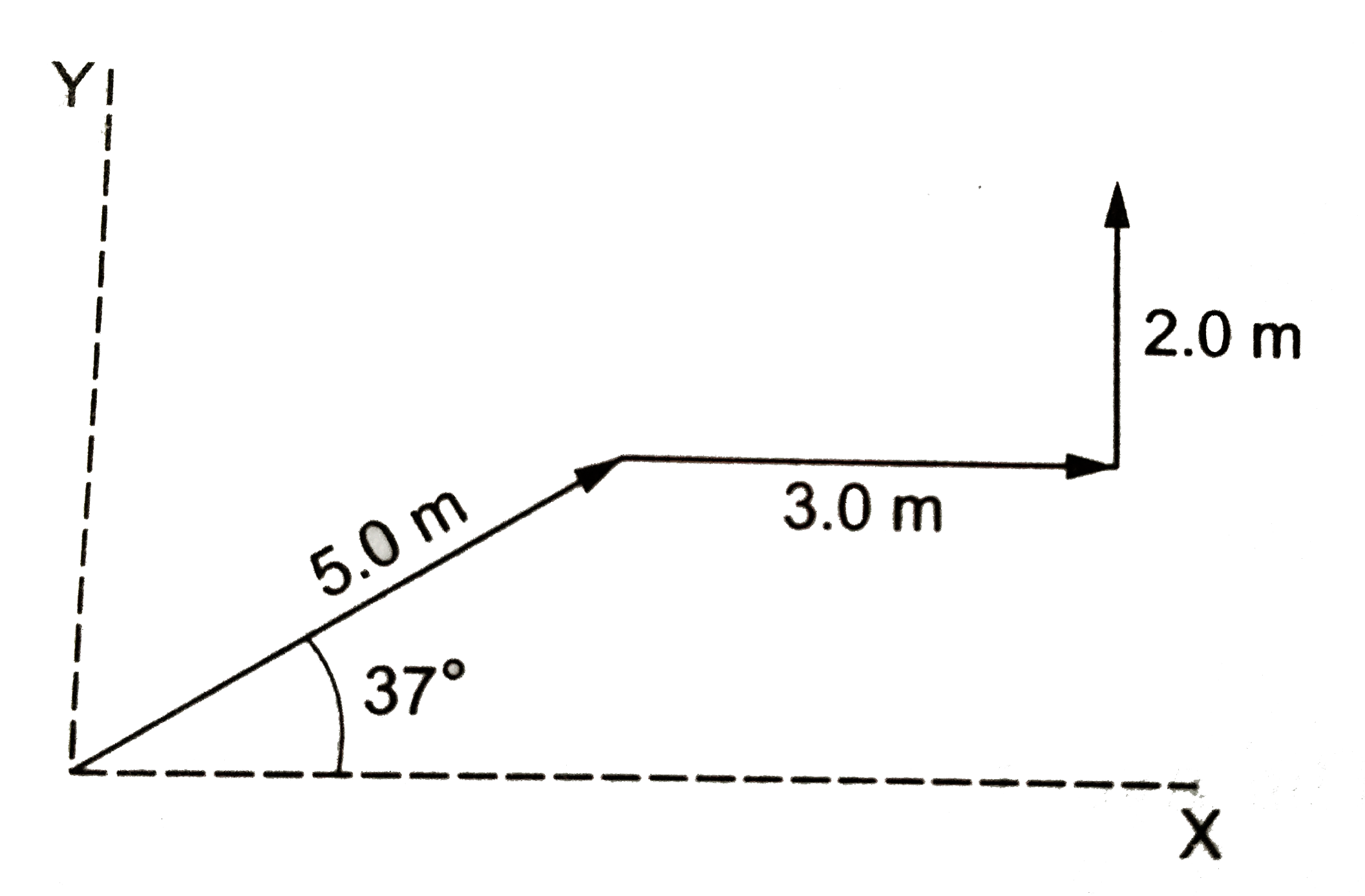 .
.
View SolutionGiven an example for which `vecA.vecB=vecC.vecB but vecA!=vecC`.
View SolutionObtain the angle between A+B and A-B if `A = 2hati +3hatj and B = hati - 2hatj.`
View SolutionDeduce the condition for the vectors `2hati + 3hatj - 4hatk and 3hati - alpha hatj + bhatk` to be parallel.
View SolutionFind the area of the parallelogram whose sides are represented by `2hati + 4hatj - 6hatk and hati +2hatk.`
View SolutionIf vectors A and B be respectively equal to `3hati - 4hatj + 5hatk and 2hati + 3hatj - 4hatk.` Find the unit vector parallel t A + B
View Solutionif `A = 2hati - 3hatj+7hatk, B = hati + 2hatj and C=hatj - hatk`. Find `A(BxxC)`
View SolutionThe x and y-components of vector A are 4 m and 6 m respectively. The x and y-components of vector A + B are 10 m and 9 m respectively. Calculate for the vector B the following:
(a) its x and y-components
(b) its length
(c ) the angle it makes with x-axis.
View SolutionThree vectors which are coplanar with respect to a certain rectangular co-ordinate system are given by `a = 4 hati - hatj, b = - 3hati + 2hatj and c =- 3hatj`
Find
(a) `a+b+c`
(b) `a+b-c`
(c ) Find the angle between `a+b+c and a+b-c`
View SolutionLet `vecA and vecB` be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angles `30^@ and 60^@` respectively, find the resultant.
View SolutionThe resultant of vectors `vec(OA) and vec(OB)` is peerpendicular to `vec(OA)`. Find the angle AOB.
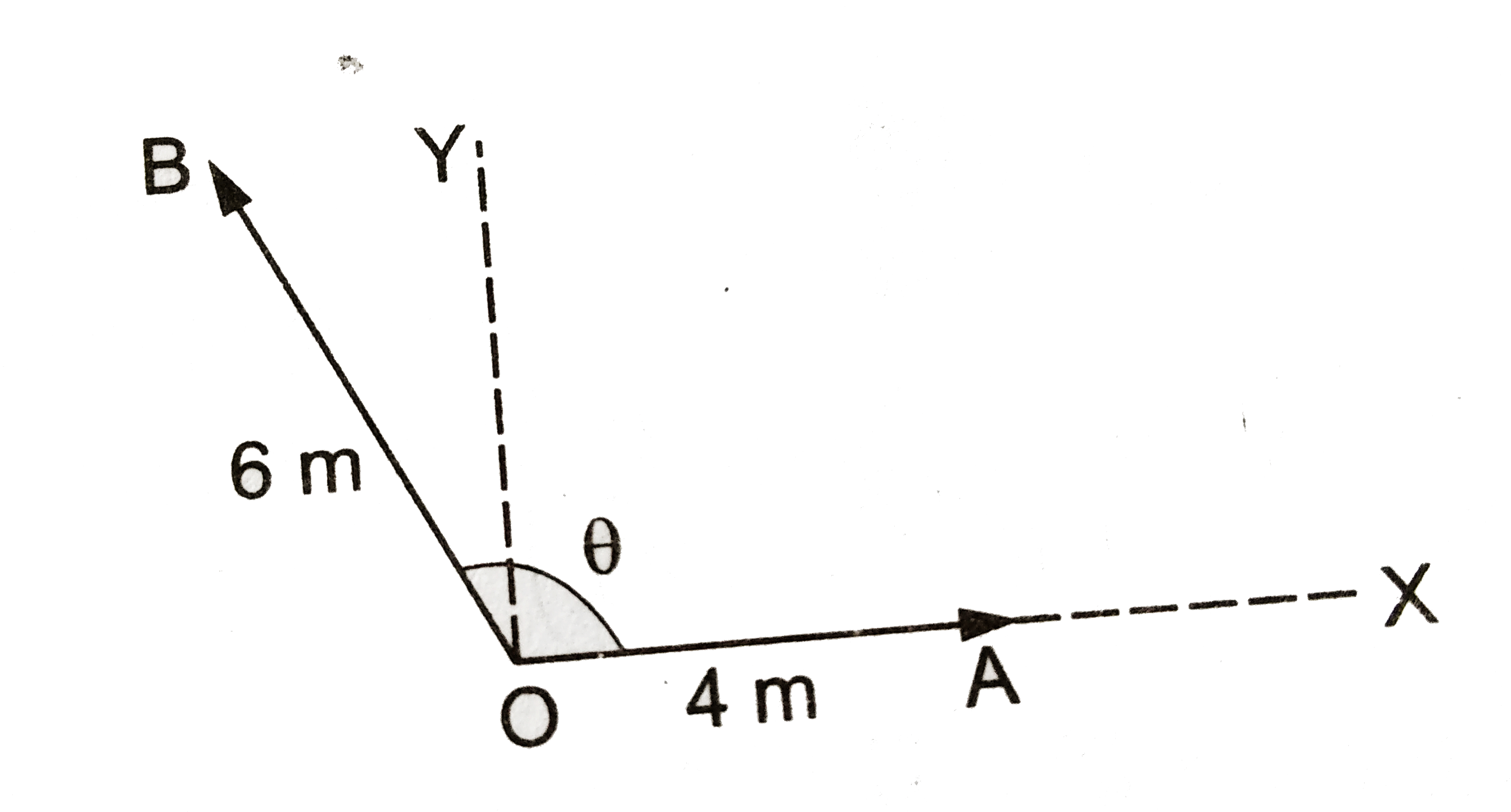
View SolutionFind the components of a vector `A = 2hati + 3hatj` along the directions of `hati + hatj and hati - hatj.`
View SolutionIf two vectors are `A = 2hati + hatj - hatk and B = hatj - 4hatk.` By calculation, prove AxxB isperpendicular to both A and B.
View SolutionThe resultant of two vector A and B is at right angles to A and its magnitude is half of B. Find the angle between A and B.
View SolutionFour forces of magnitude P, 2P, 3P and 4P act along the four sides of a square ABCD in cyclic order. Use the vector method to find the magnitude of resultant force.
View SolutionIf P + Q = R and P - Q = S, prove that `R^2 + S^2 = 2(P^2 + Q^2)`
View SolutionIn an `Delta ABC` as showin in Fig. 2 . (2) .71 (a) prove
that ` a/(sin A) =b/(sin B) =C/(sin C)`.
View Solution
Subjective questions and complete solutions for chapter VECTORS of DC PANDEY ENGLISH of Class 11