Complete Solutions to Solved Examples of chapter VECTORS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | VECTORS |
| DC PANDEY | Solved Examples |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
In the shown fig . 5.12 (a) , (b) and (c ) , find the angle between A and B .
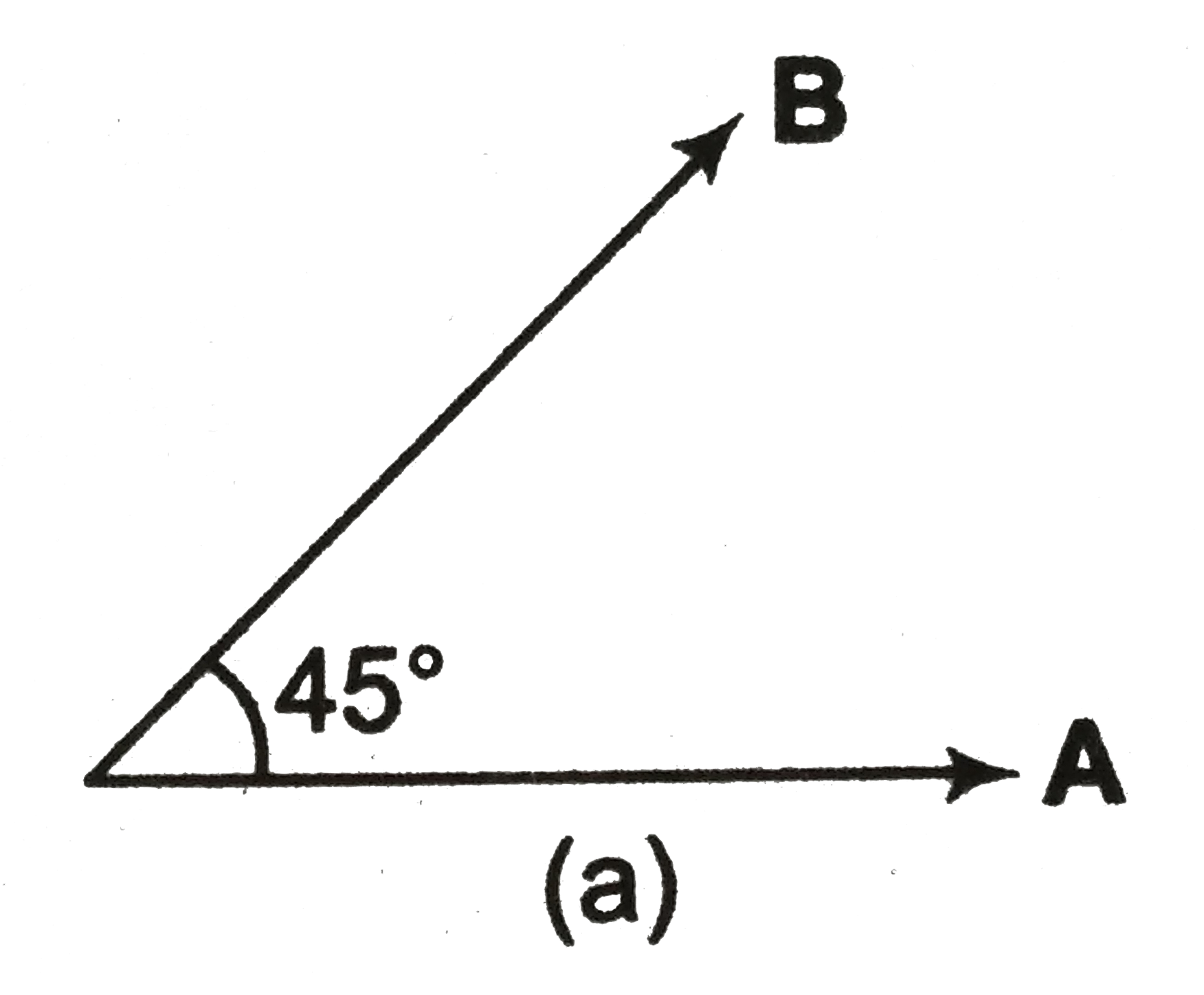
(b)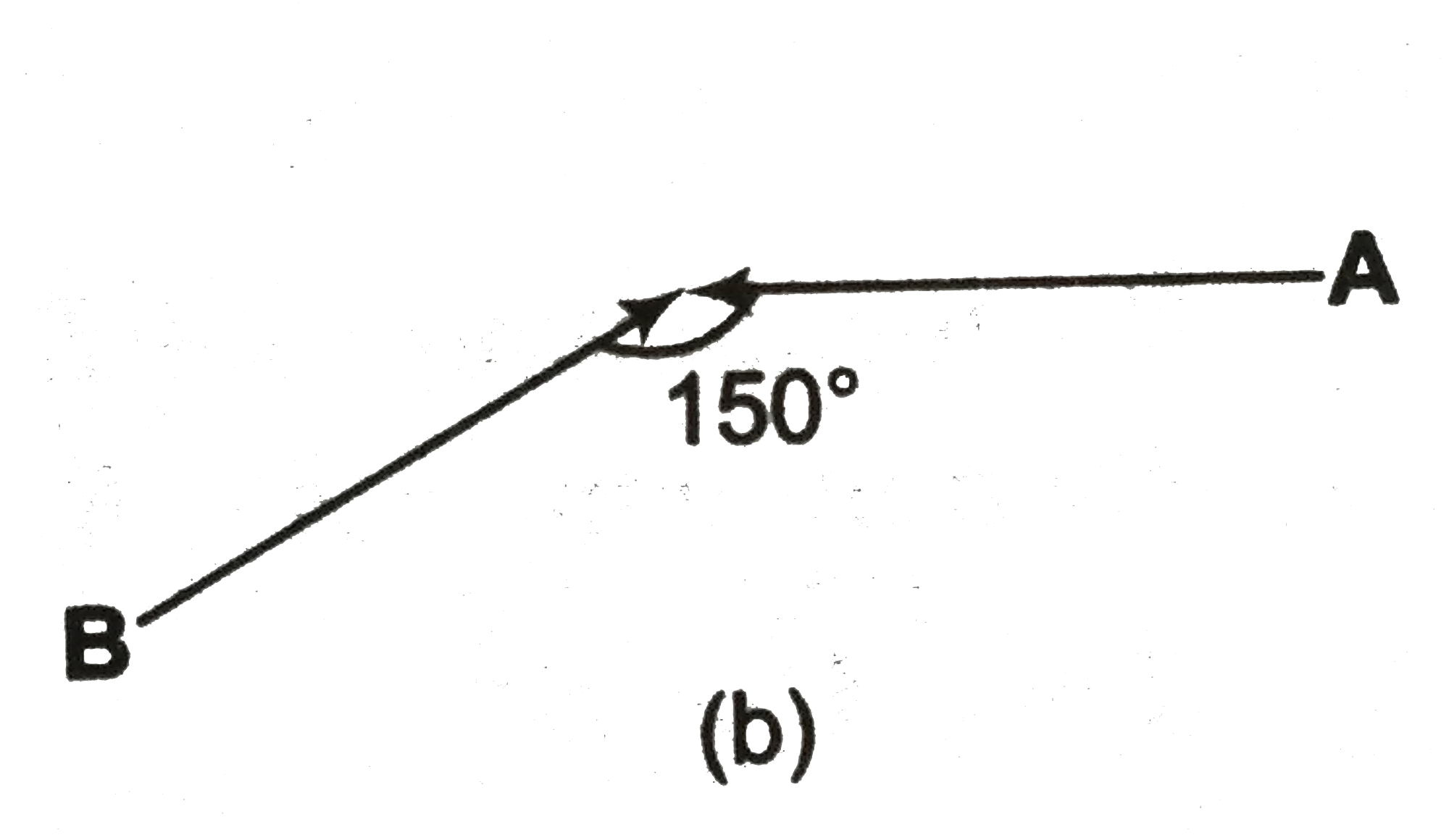
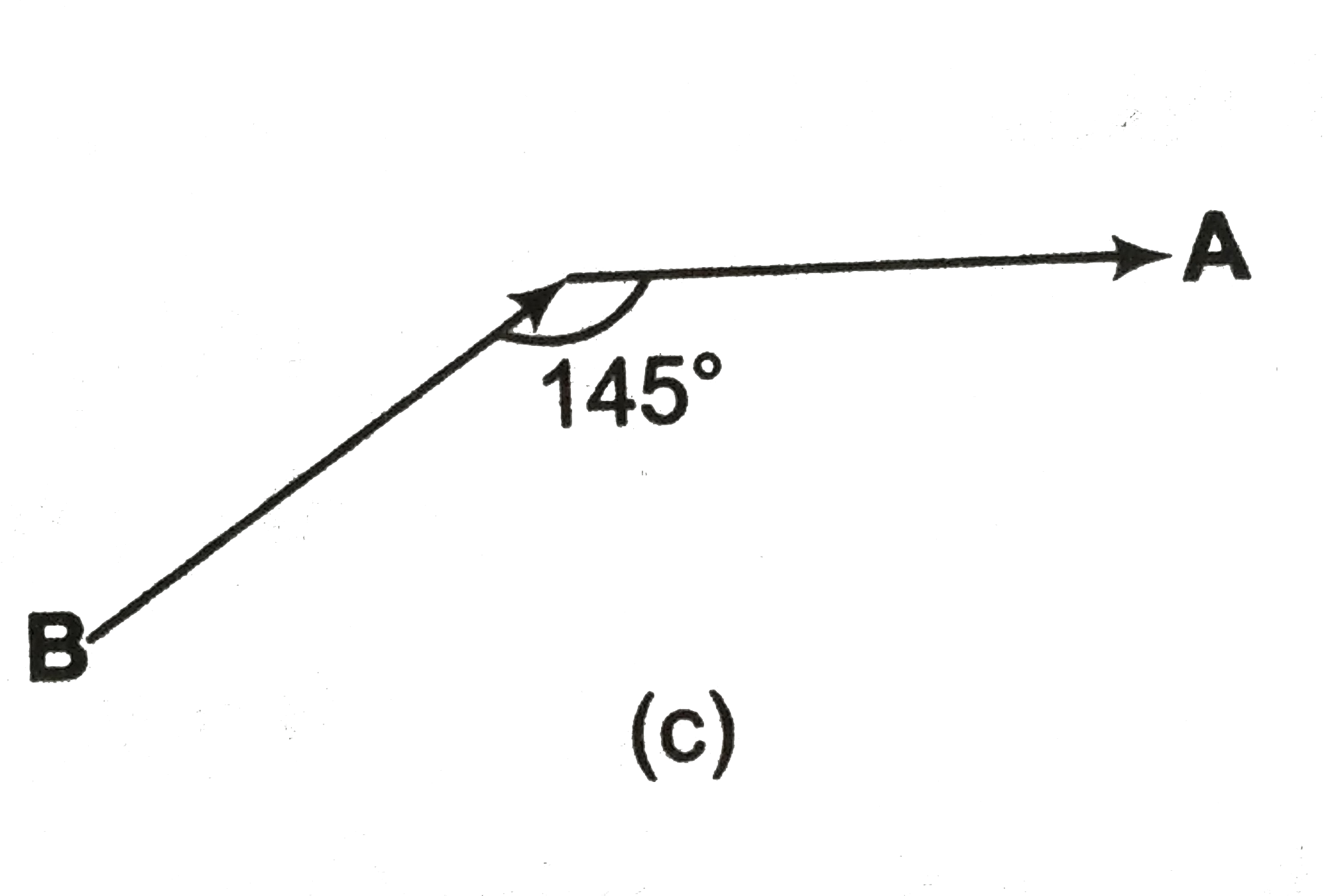 .
.
View SolutionWhat is the angle between a and `-(3)/(2) a`.
View SolutionFind A+B and A-B in the diagram shown in figure. Given A=4 units and B=3 units.
 .
.
View SolutionA force`F` has magnitude of `15N`. Direction of `F` is at `37^(@)` from nagative x-axis towards posititve y-axis. Represent F in terms of `hat i` and `hat J` .
View SolutionFind magnitude and directon of a vector, `A = (6hati - 8 hat j)`.
View SolutionResolve a weight of 10N in two directions which are parallel and perpendiular to a slope inclined at `30^@` to the horizontal.
View SolutionResolve horizontally and vertically a force f =8 N which makes an angle of `45^@` with the horizontal.
View SolutionObtain the magnitude of 2A - 3B if
`A = hati +hatJ- 2 hat k and b = 2 hat I - hat j+hat k` .
View SolutionWork done by a force F on a body is W = F .s, where s is the displacement of body. Given that under a force `F = (2 hat I +3 hat j +4 hat k)` N a body is displaced from position vector `r_1 = (2 hat I +3 hat j + hat k)` m to the position vector `r_2 = (hat i +hat j+ hat k)` m. Find the work done by this force.
View SolutionFind the angle between two vectors `A= 2 hat i + hat j - hat k` and `B=hat i - hat k` .
View SolutionProve that the vectors `A = 2 hati - 3 j+hat k` and `B= hat i+hat j + hat k` are mutually perpendicular.
View SolutionShow that the vector `A = (hati) - (hatj) + 2 hatk` is parallel to a vector `B = 3hati - 3hat + 6hatk`.
View SolutionLet a force F be acting on a body free to rotate about a point O and let r the position vector of ant point P on the line of aciton of the force. Then torque `(tau)` of this force abot point O is defined as ` tau = rxxF` Given, `F = (2hati + 3hatj - hatk)N and r = (hati- hatj+6hatk)m` Find the torque of this force.
View SolutionFind component of vector A +B along (i) x-axis, (ii) C. Given `A = hati - 2hatj, B=2hati+3hatk` and `C = hati +hatj`.
View SolutionFind the angle that the vector `A = 2hati+3hatj-hatk` makes with y-axis.
View SolutionIf a and b are the vectors AB and BC determined by the adjacent sides of a ragular hexagon. What are the vectors determined by the other sides taken is order?
View Solutionif `axxb = bxxc != 0` with a `!= -c` then show that a+c = kb, where k is scalar.
View Solutionif `A = 2hati - 3hatj+7hatk, B = hati + 2hatj and C=hatj - hatk`. Find `A(BxxC)`
View SolutionFind the resultant of the three vectors `vec(OA), vec(OB)` and `vec(OC)` shown in figure. Radius of the circle is R.

View SolutionProve that `|axxb|^2 =a^2b^2 - (a.b)^2`
View SolutionShow that the vectors `a =3hati - 2hatj+hatk, b=hati - 3hatj+5hatk` and `c=2hatj+hatj-4hatk` form a right angled triangle.
View SolutionLet A,B and C be the unit vectors . Suppose that A.B=A.C =0 and the angle between B and C is `(pi)/(6)` then prove that `A = +-2(BxxC)`
View SolutionA particle moves on a given straight line with a constant speed v. At a certain time it is at a point P on its straight lline path.O is a fixed point. Show than `vec(OP)xxvec upsilon` is independent of the position P.?
View SolutionProve that the mid-point of the hypotenuse of right angled triangle is equidistant from its vertices.
View Solution
Solved Examples questions and complete solutions for chapter VECTORS of DC PANDEY ENGLISH of Class 11