Complete Solutions to Example of chapter MOTION IN A PLANE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| DC PANDEY NEET | Example |
| Number Of Questions | 73 |
| Academic Year | 2023-24 |
A scooter is moving along a straight line AB covers a distance of 360 m in 24 s and returns back from B to C and coveres 240 m in 18 s. Find the total distance travelled by the scooter.
View SolutionA wheel completes 2000 revolutions to cover the 9.5 km. distance. then the diameter of the wheel is
View SolutionA man starts from his home and walks 50 m towards, then he turns towards east and walks 40 m and then reaches to his office after moving 20 m towards south.
(i) What is the total distance covered by the man from his home to office ?
(ii) What is his displacement from his home to office ?
View SolutionAn object covers 1/4 of the circular path, what will be the ratio of the distance and displacement of the object ?
View SolutionDisplacement of a person moving from X to Y along a semicircular path of radius r is 200 m. What is the distance travelled by him ?
View SolutionAn athlete complete one round of a circular track of diameter `200 m` in `40 s`. What will be the distance covered and the displacement at the end of `2` minutes `20 s` ?
View SolutionThe distance covered by an object (in meter) is given by
`s=8 t^(3)-7t^(2)+5t`
Find its speed at t = 2 s.
View SolutionAbdul while driving to school, computes the average speed for his trip to be `20 kmh^(-1)`. On his return trip along the same route, there is less traffic and the average speed is `40 kmh^(-1)`. What is the average speed for Abdul's trip ?
View SolutionA car moves from `X` to `Y` with a uniform speed `v_u` and returns to `X` with a uniform speed `v_d`. The average speed for this round trip is :
(a) `(2v_(d)v_(u))/(v_(d)+v_(u))` (b) `sqrt(v_(u)u_(d))` (c) `(v_(d)v_(u))/(v_(d)+v_(u))` (d) `(v_(u)+v_(d))/(2)`
View SolutionA particle travels along a straight line. It covers halg the distance with a speed (v). The remaining part of the distance was covere with speed `v_(1)` for half the time and with speed `v_(2)` for the other half the time . Find the average speed of the particle over the entire motion.
View SolutionA car covers the first half of the distance between two places at a speed of `40 kmh^(-1)` and second half at `60 kmh^(-1)` Calculate the average speed of the car.
View SolutionIn one second, a particle goes from point A to point B moving in a semicircle (Fig). Find the magnitude of the average velocity.
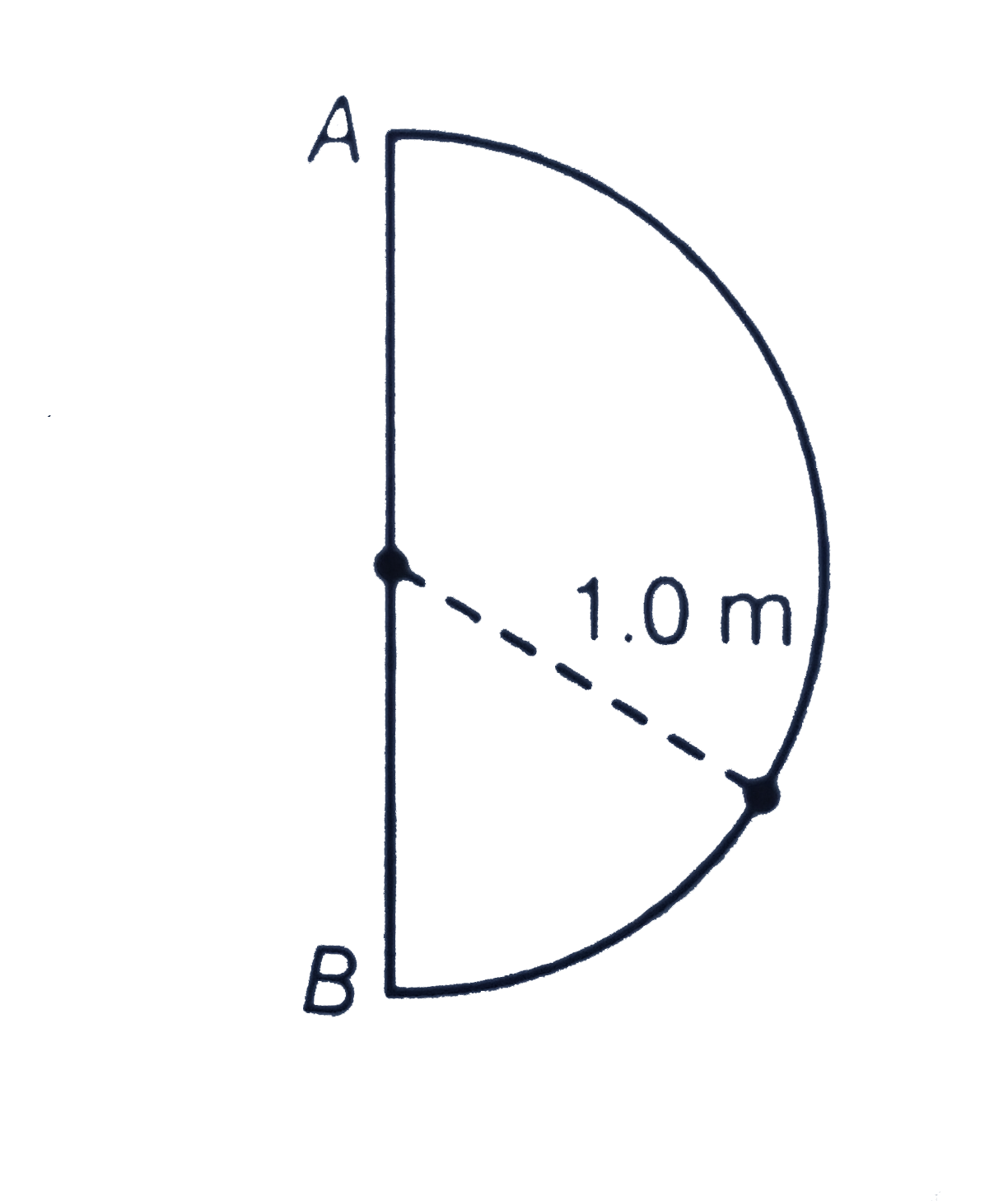
View SolutionA farmer has to go 500 m due north, 400 m due east and 200 m due south to reach his field. If he takes 20 min to reach the field.
(a) What distance he has to walk to reach the field ?
(b) What is the displacement from his house to the field ?
(c) What is the average speed of farmer during the walk ?
(d) What is the average velocity of farmer during the walk ?
View SolutionJoseph jogs from one end A to the other end B of a straight 300 m road in 2 min 50 s and then turns around and jogs 100 m back to point C in another 1 min. What are Joseph's average speeds and velocities in jogging (i) from A to B and (ii) from A to C ?
View SolutionA car is moving along a straight line OP as shown in the figure. It moves from O to P in 18 s and returns from P to Q in 6 s. Which of the following statements is not correct regarding the motion of the car ?
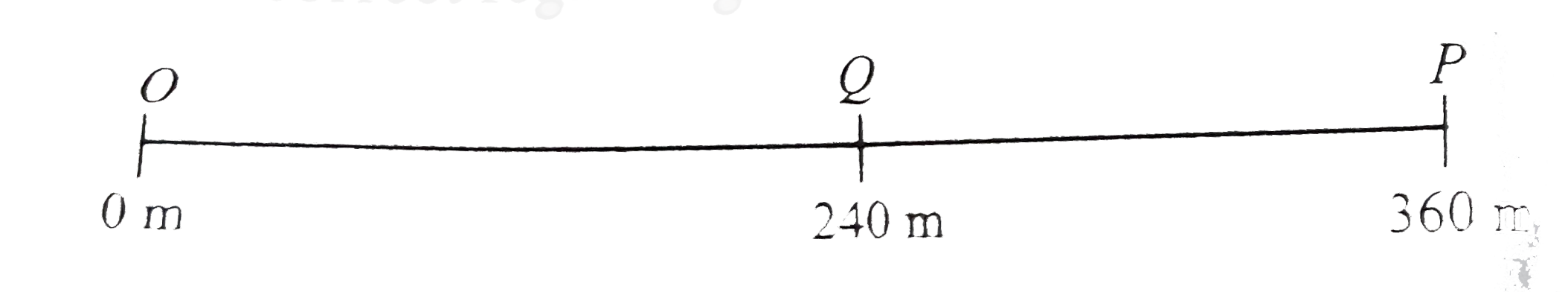
View SolutionThe position of object moving along an x-axis is given by `x=3t-4t^(2)+t^(3)`, where x is in meters and t in seconds. Find the position of the object at the following values of t : (i) 2s, (ii) 4s, (iii) What is the object's displacement between t = 0 s and t = 4 s ? and (iv) What is its average vvelocity for the time interval from t = 2 s to t = 4 ?
View SolutionThe velocity of particle moving in the positive direction of x axis varies as `v=alphasqrt(x)`, where `alpha` is a positive constnat. Assuming that at moment `t=0`, the particle was located at the point x=0. find.
(a) the time dependence of the velocity and the acceleration of the particle.
(b) the mean velocity of the particle averaged over the time that the particle takes to cover first s meters of the path
View SolutionThe distance travelled by an object moving along a straight line is directly proportional to the square of the time. Its acceleration
View SolutionGive examples where a. the velocity of a particle is zero but its acceleration is not zero. b.the velocity is opposite in direction to the acceleration, c. the velocity is perpendicular to the acceleration.
View SolutionThe velocity of a particle is given by `v=(2t^(2)-3t+10)ms^(-1)`. Find the instantaneous acceleration at t = 5 s.
View SolutionA particle is moving with a velocity of `v=(3+ 6t +9t^2) m/s.` Find out
(a) the acceleration of the particle at `t=3 s.`
(b) the displacement of the particle in the interval `t=5s` to `t=8 s.`
View SolutionThe motion of a particle along a straight line is described by the function `x=(2t -3)^2,` where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at `t=2 s.`
(b) the velocity of the particle at origin.
View SolutionThe radius vector of a point depends on time t, as
`r = c t +(b t^(2))/(2)`
where c and b are constant vectors. Find the modulus of velocity and acceleration at any time t.
View SolutionA particle is moving in a straight line. Its displacement at any instant t is given by `x = 10 t+ 15 t^(3)`, where x is in meters and t is in seconds. Find
(i) the average acceleration in the intervasl t = 0 to t = 2s and
(ii) instantaneous acceleration at t = 2 s.
View Solution(i) What does `|(dv)/(dt)|` and `(d|V|)/(dt)` represent ?
(ii) Can these be equal ?
(iii) Can `(d|V)/(dt)= 0` while `|(dV)/(dt)ne0` ?
(iv) Can `(d|V|)/(dt)ne 0` while `|(dv)/(dt)|=0` ?
View SolutionA car was movig at a rate of `18 kmh^(-1)` . When the brakes were applied, it comes to rest in a distance of 100 m. Calculate the retardation produced by the brakes.
View SolutionTwo cars start off a race with velocities 2m`//`s and 4m`//`s travel in straight line with uniform acceleration `2m//s^(2) and 1m//s^(2)` respectively. What is the length of the path if they reach the final point at the same time ?
View SolutionA body starting from rest has an acceleration of `4ms^(-2)` . Calculate distance travelled by it in 5th second.
View SolutionA train, travelling at `20 km//hr` is approaching a platform. A bird is sitting on a pole on the platform. When the train is at a distance of 2 km from pole, breakes are applied which produce auniform deceleration in it. At that instant the bird flies towards the train at `60 km//hr` and after touching the nearest point on the train flies back to the pole and then flies towards the train and continues repeating itself. Calculate how much distance will the bird have flown before the train stops?
View SolutionA particle starts with an initial velocity and passes successively over the two halves of a given distance with constant accelerations `a_1 and a_2` respectively. Show that the final velocity is the same as if the whole distance is covered with a uniform acceleration `(a_1 + a_2)/2 .`
View SolutionIn a car race, car A takes a time t less than car B at the finish and passes the finishing point with speed v more than that of the car B. Assuming that both the cars start from rest and travel with constant acceleration `a_1 and a_2` respectively. Show that `v=sqrt (a_1 a_2) t.`
View SolutionA particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of displacement (a) in successive second and (b) in successive time interval `t_(0)`.
View SolutionVelocity and acceleration of a particle at time `t=0`are `u=(2 hati+3 hatj) m//s and a=(4 hati+3 hatj) m//s^2` respectively. Find the velocity and displacement if particle at `t=2s.`
View SolutionA ball is thrown upwards from the top of a tower `40 m` high with a velocity of `10 m//s.` Find the time when it strikes the ground. Take `g=10 m//s^2`.
View SolutionA pobble is thrown vertically upwards from a bridge with an initial velocity of `4.9 ms^(-1)` . It strikes the water after 2 s. If acceleration due to gravity does the pebble strike the water ?
View SolutionA rocket is fired vertically up from the ground with a resultant vertical acceleration of `10 m//s^2.` The fuel is finished in 1 min and it continues to move up. (a) What is the maximum height reached? (b) Afte2r how much time from then will the maximum height be reached?(Take `g= 10 m//s^2`)
View SolutionA juggler throws balls into air. He throws one when ever the previous one is at its highest point. If he throws n balls each second, the height to which each ball will rise is
View SolutionFrom an elevated point A, a stone is projected vertically upwards. When the stone reaches a distance h below A, its velocity is doubleof what it was at a height h above A. Show that the greatest height attained by the stone is `5/3 h.`
View SolutionA ball is thrown vertically upwards with a velocity of `20 m s^(-1)` from the top of a multistore building of 25 m high. How high will the ball rise? (Take g = `10 m s^(-2)`)
View SolutionA ball is thrown upwards from the ground with an initial speed of u. The ball is at height of `80m` at two times, the time interval being 6 s. Find u. Take `g=10 m//s^2.`
View SolutionA particle of mass 1 kg has a velocity of `2m//s`. A constant force of 2N acts on the particle for 1s in a direction perpendicular to its initial velocity. Find the velocity and displacement of the particle at the end of 1 s.
View SolutionAn open elevator is ascending with constant speed `v=10m//s.` A ball is thrown vertically up by a boy on the lift when he is at a height `h=10m` from the ground. The velocity of projection is `v=30 m//s` with respect to elevator. Find
(a) the maximum height attained by the ball.
(b) the time taken by the ball to meet the elevator again.
(c) time taken by the ball to reach the ground after crossing the elevator.
View SolutionA particle is thrown vertically upwards from the surface of the earth. Let `T_(P)` be the time taken by the particle to travel from a point P above the earth to its highest point and back to the point P. Similarly, let `T_(Q)` be the time taken by the particle to travel from another point Q above the earth to its highest point and back to the same in terms of `T_(P), T_(Q)` and H, is :-
View SolutionDrop of water fall at regular intervals from roof of a building of height (H=16 m), the first drop striking the ground at the same moment as the fifth drop falls from the roof. The distances between separate drops in air as the first drop reaches the ground are.
View SolutionA ball is dropped from the top of a tower. After 2 s another ball is thrown vertically downwards with a speed of `40 ms^(-1)`. After how much time and at what distance below the top of tower the balls meet ?
View SolutionVelocity-time equation of a particle moving in a straight line is, `v=(10+2t+3t^2)` (SI units) Find
(a) displacement of particle from the mean position at time `t=1s,` if it is given that displacement is 20m at time `t=0`.
(b) acceleration-time equation.
View SolutionDisplacement-time equation of a particle moving along x-axis is `x=20+t^3-12t` (SI units)
(a) Find, position and velocity of particle at time t=0.
(b) State whether the motion is uniformly accelerated or not.
(c) Find position of particle when velocity of particle is zero.
View SolutionWith the help of the given velocity - time graph, find the
(i) displacement in first three seconds and
(ii) acceleration for the graph.

View SolutionAcceleration - time graph of a particle moving in a straight line is shown in figure. Velocity of particle at time t = 0 is `2 ms^(-1)`. Find velocity at the end of fourth second.

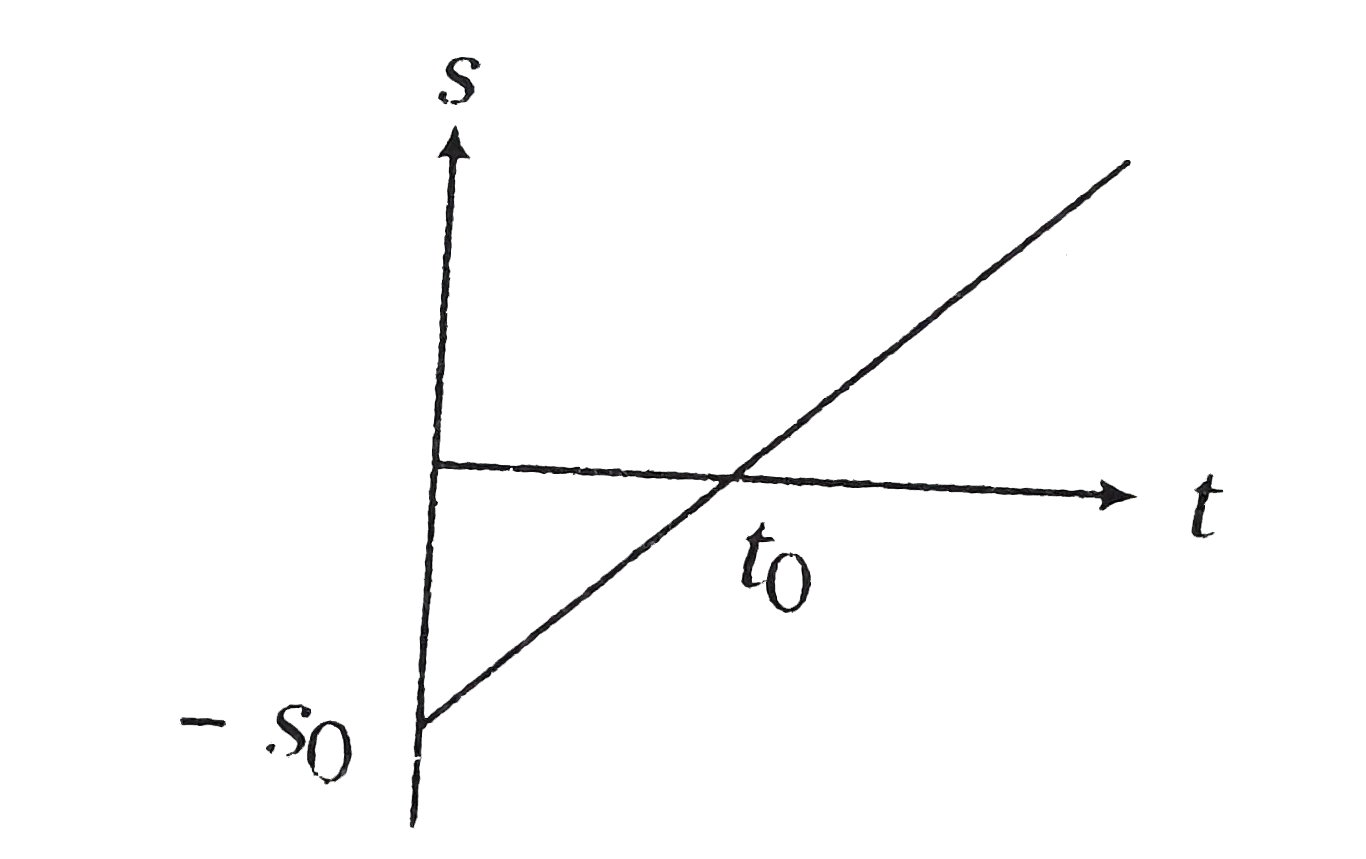
View SolutionDisplacement - time graph of particle moving in a straight line is as shown in figure. State whether the motion is accelerated or not. Describe the motion in detail. Given,
`s_(0)=20 m` and `t_(0) = 4 s`.
View SolutionA particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
View SolutionA car accelerates from rest at a constant rate `alpha` for some time, after which it decelerates at a constant rate `beta,` to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionThe acceleration versus time graph of a particle moving along a straight line is shown in the figure. Draw the respective velocity-time graph Given `v=0` at `t=0.`

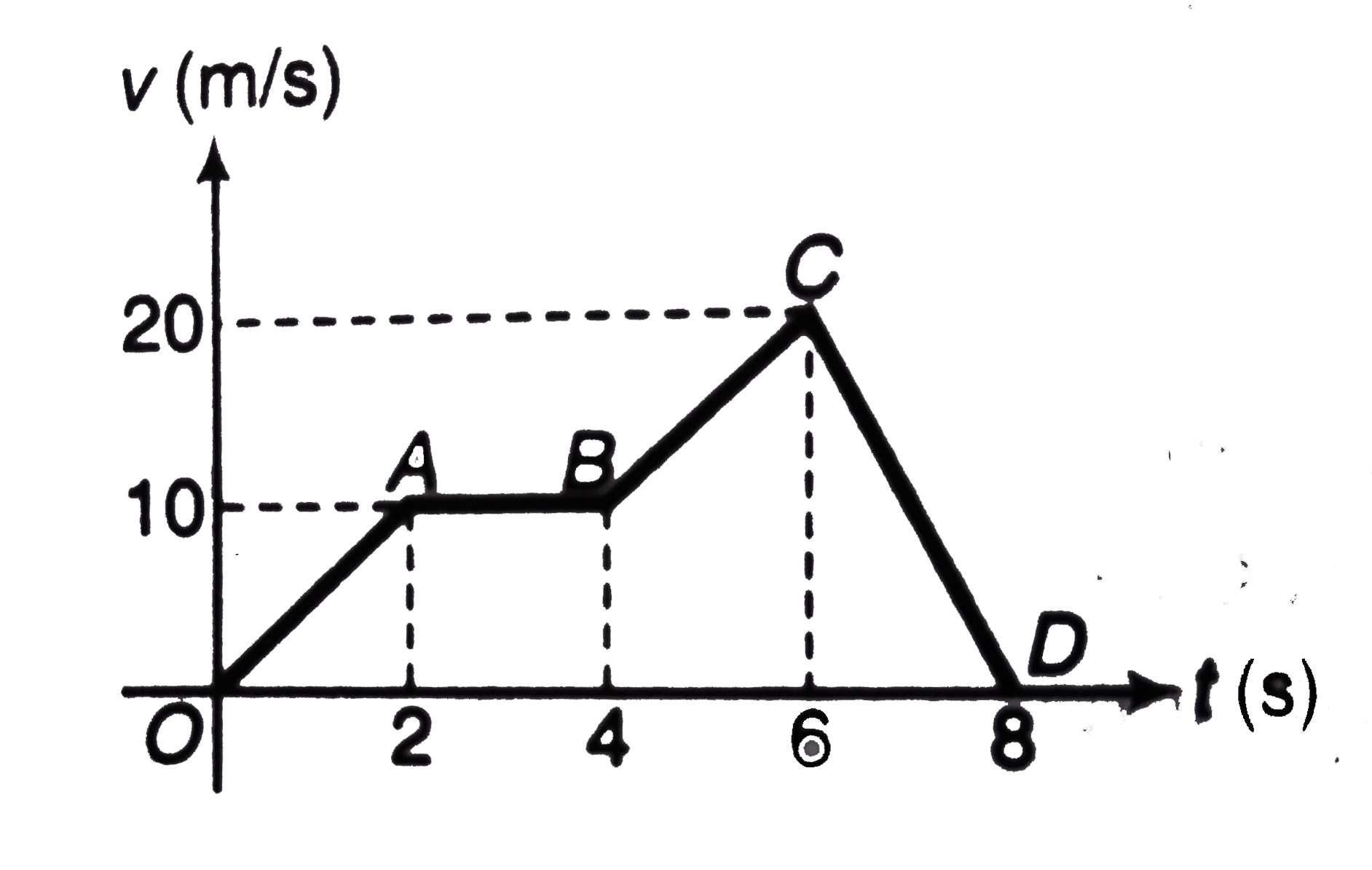
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. Plot the corresponding displacement-time graph of the particle if at time `t=0,` displacement `s=0.`
View SolutionA rocket is fired vertically upwards with a net acceleration of `4 m//s^2` and initial velocity zero. After `5s` its fuel is finished and it decelerates with g. At the highest point its velocity becomes zero. Then, it accelerates downwards with acceleration g and return back to ground. Plot velocity-time and displacement -time graphs for the complete journey. Take `g=10m//s^2.`
View SolutionAnoop is moving due east with a velocity of `1 m//s` and Dhyani is moving due west with a velocity of `2 m//s.` what is the velocity of Anoop with respect to Dhyani?
View SolutionTwo parallel rail tracks run north-south. On one track train A moves noth with a speed of `54 km h^(-1)` and on the other track train B moves south with a speed of `90 km h^(-1)`. The velocity of train A with respect to train B is
View SolutionA man A moves due to East with velocity `6 ms^(-1)` and another man B moves in `N-30^(@)E` with `6 ms^(-1)` . Find the velocity of B w.r.t. A.
View SolutionBuses A and B are moving in the same direction with speed `20 ms^(-1)` and `15 ms^(-1)` respectively. Find the relative velcoity of A w.r.t. B and relative velocity of B w.r.t. A.
View SolutionCar A has an acceleration of `2m//s^2` due east and car B,`4 m//s^2.` due north. What is the acceleration of car B with respect to car A?
View SolutionA police van moving on a highway with a speed of `30 km h^(-1)` Fires a bullet at a thief's car speeding away in a same direction with a speed of `192 km h^(-1)`. If the muzzle speed of the buller is `150 m s^(-1)`, with what speed does the bullet hit thief's car? .
 .
.
View SolutionDelhi is at a distance of 200 km from Ambala. Car A set out from Ambala at a speed of `30 kmh^(-1)` and car B set out at the same time from Delhi at a speed of `20 kmh^(-1)`. When they will meet each other ? What is the distance of that meeting point from Ambala ?
View SolutionTwo cars are travelling towards each other on a straight road with velocities `10 m s^(-1) and 12 m s^(-1)` respectively. When they are 150 m apart, both drivers apply their brakes and each car decelerates at `2 m s^(-2)` until it stops. How far apart will they be when they have come to rest?
View SolutionTo a man walking at the rate of `3 km//h` the rain appear to fall vetically douwnwards. When he increases his speed `6 km//h` it appears to meet him at an angle of `45^@` with vertically. Find the speed of rain.
View SolutionA man crosses a river in a boat. If he cross the river in minimum time he takes `10 min` with a drift `120 m.` If he crosses the river taking shortest path, he takes `12.5 min,` find
(a) width of the river
(b) velocity of the boat with respect to water
(c) speed of the current
View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point B? In which direction should he swim?
View SolutionA man can row a boat with 4km/h in still water, if he is crossing a river where the current is 2 km/h.
(a) In what direction will his boat be holded, if he wants to reach a point on the other bank, directly opposite to starting point?
(b) If width of the river 4km, how long will the man take to cross the river, with the condition in part (a)?
(c) In what direction shou ld he heat the boat if he wants to cross the river in shorest time and what is this minimum time?
(d) How long will it take him to row 2 km up the stream and then back to his starting point?
View SolutionA boat moves relative to water with a velocity `v` which is `n` times less than the river flow velocity `u`. At what angle to the stream direction must the boat move to minimize drifting ?
View SolutionCar A and car B start moving simultaneously in the same direction along the line joining them. Car A moves with a constant acceleration `a=4 m//s^2,` while car B moves with a constant velocity `v=1 m//s.` At time `t=0,` car A is `10 m` behind car B. Find the time when car A overtake car B.
View SolutionAn open lift is moving upward with velocity `10 m//s.` It has an upward acceleration of `2 m//s^2.` A ball is projected upwards with velocity `20 m//s` relative to ground. Find
(a) time when ball again meets the lift
(b) displacement of lift and ball at that instant.
Take `g=10 m//s^2`
View SolutionTwo ships A and B are `10 km` apart on a line running south to north. Ship A farther north is streaming west at `20 km//h` and ship B is streaming north at `20 km//h.` What is their distance of closest approach and how long do they take to reach it?
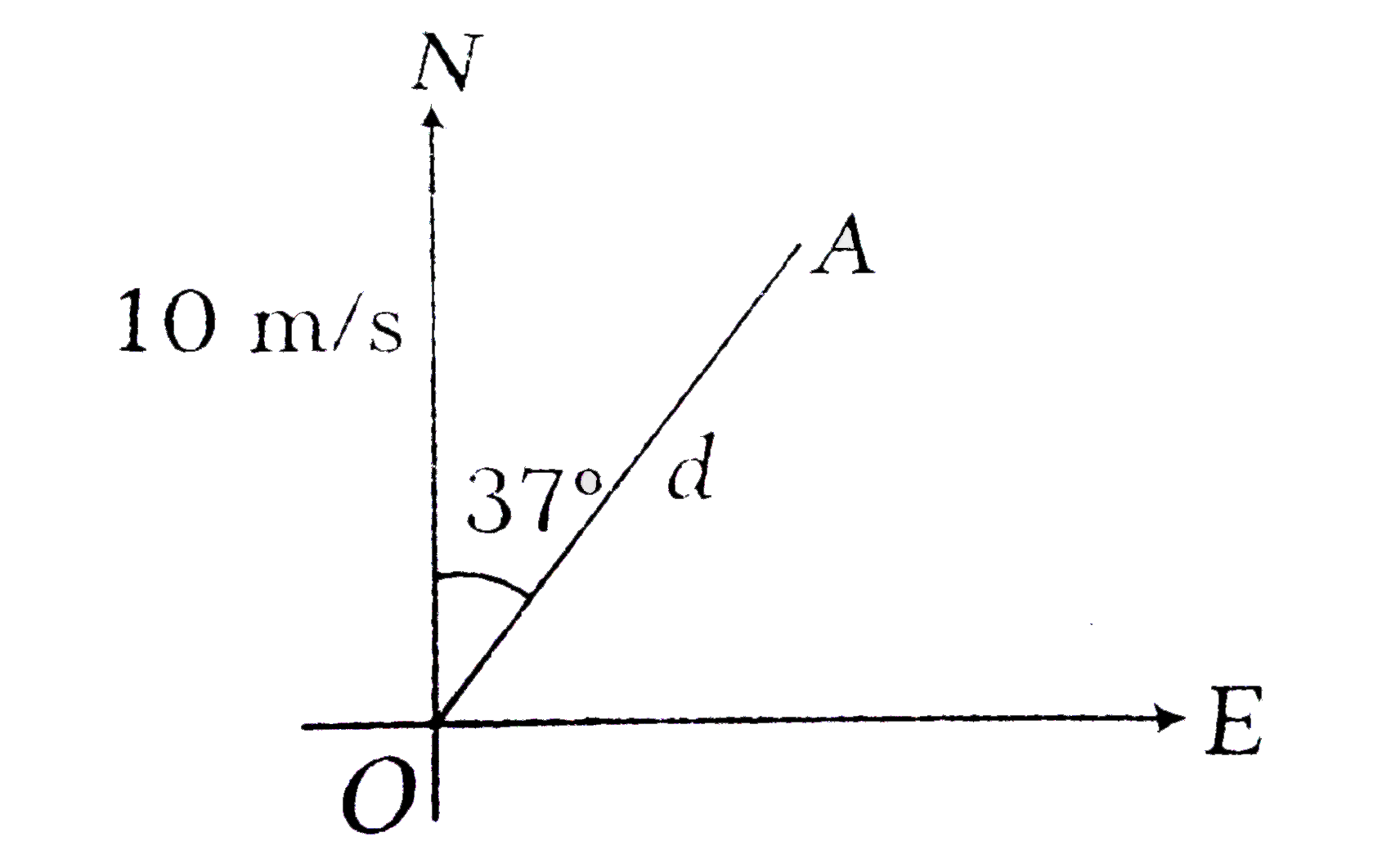
View SolutionAn aeroplane has to go from a point O to another point A, at distance d due `37^(@)` East of North. A wind is blowing due North at a speed of `10 ms^(-1)`. The air speed of the plane is v. (i) Find the direction in which the pilot should head the plane to reach the point A. (ii) Find the time taken by the plane to go from O to A.
View SolutionAn aircraft flies at `400 km//h` in still air. A wind of `200sqrt2 km//h` is blowing from the south towards north. The pilot wishes to travel from A to a point B north east of A. Find the direction he must steer and time of his journey if `AB=1000 km.`
View Solution
Example questions and complete solutions for chapter MOTION IN A PLANE of DC PANDEY ENGLISH of Class 11