Complete Solutions to (A) Taking it together of chapter MOTION IN A PLANE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| DC PANDEY NEET | (A) Taking it together |
| Number Of Questions | 75 |
| Academic Year | 2023-24 |
A bo walks to his school at a distance of 6 km with constant speed of `2.5 kmh^(-1)` and walks back with a constant speed of `4 kmh^(-1)`. His average speed for round trip expressed in `kmh^(-1)`, is
View SolutionA man walks on a straight road from his home to market 2.5 km away with speed of 5 km/h Finding the market closed, he instantly turns and walks back with a speed of 7.5 km/h. What is the magnitude of average velocity and average speed of the man over the interval of time (i) 0 to 30 min (ii) 0 to 50 min (iii) 0 to 40 min ?
View SolutionThe distance travelled by a particle starting from rest and moving with an acceleration `(4)/(3) ms^-2`, in the third second is.
View SolutionA particle is moving along x-direction with a constant acceleration a. The particle starts from `x=x_0` position with initial velocity u. We can define the position of the particle with time by the relation
`x=x_0+ut+(1)/(2)at^2`
plot the position of the particle in relation with time is following situations
(i) If initial position of the particle is on negativ x-axis, initial velocity is positive and acceleration is negative.
(ii) If initial position is positive, initial velocity is negative and acceleration is positive.
View SolutionA particle moves along x-axis as `x=4(t-2)+a(t-2)^2`
Which of the following is true?
View SolutionA car moving with a velocity of 10m/s can be stopped by the application of a constant force F In a distance of 20m. If the velocity of the car is 30m/s. It can be stopped by this force in
View SolutionA vehicle travels half the distance (L) with speed ` V_1` and the other half with speed ` V_2`, then its average speed is .
View SolutionThe x and y coordinates of a particle at any time t are given by `x=7t+4t^2` and `y=5t`, where x and t is seconds. The acceleration of particle at `t=5`s is
View SolutionA body A starts from rest with an accceleration `a_1`. After 2 seconds, another body B starts from rest with an acceleration `a_2`. If they travel equal distances in the `5^(th)` seconds, after the start of A, then the ratio `a_1 : a_2` is equal to
View SolutionFigure given shows the distance - time graph of the motion of a car. It follows from the graph that the car is
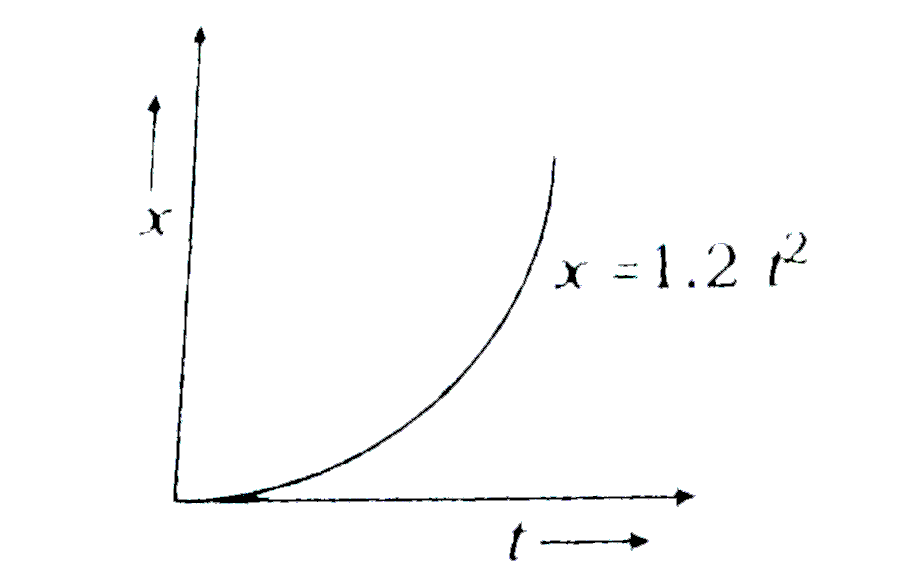
View SolutionWhich of the following speed - time `(upsilon-t)` graph is physically possible ?
View SolutionThe displacement (x)-time (t) graph of a particle is shown in figure. Which of the following is correct ?
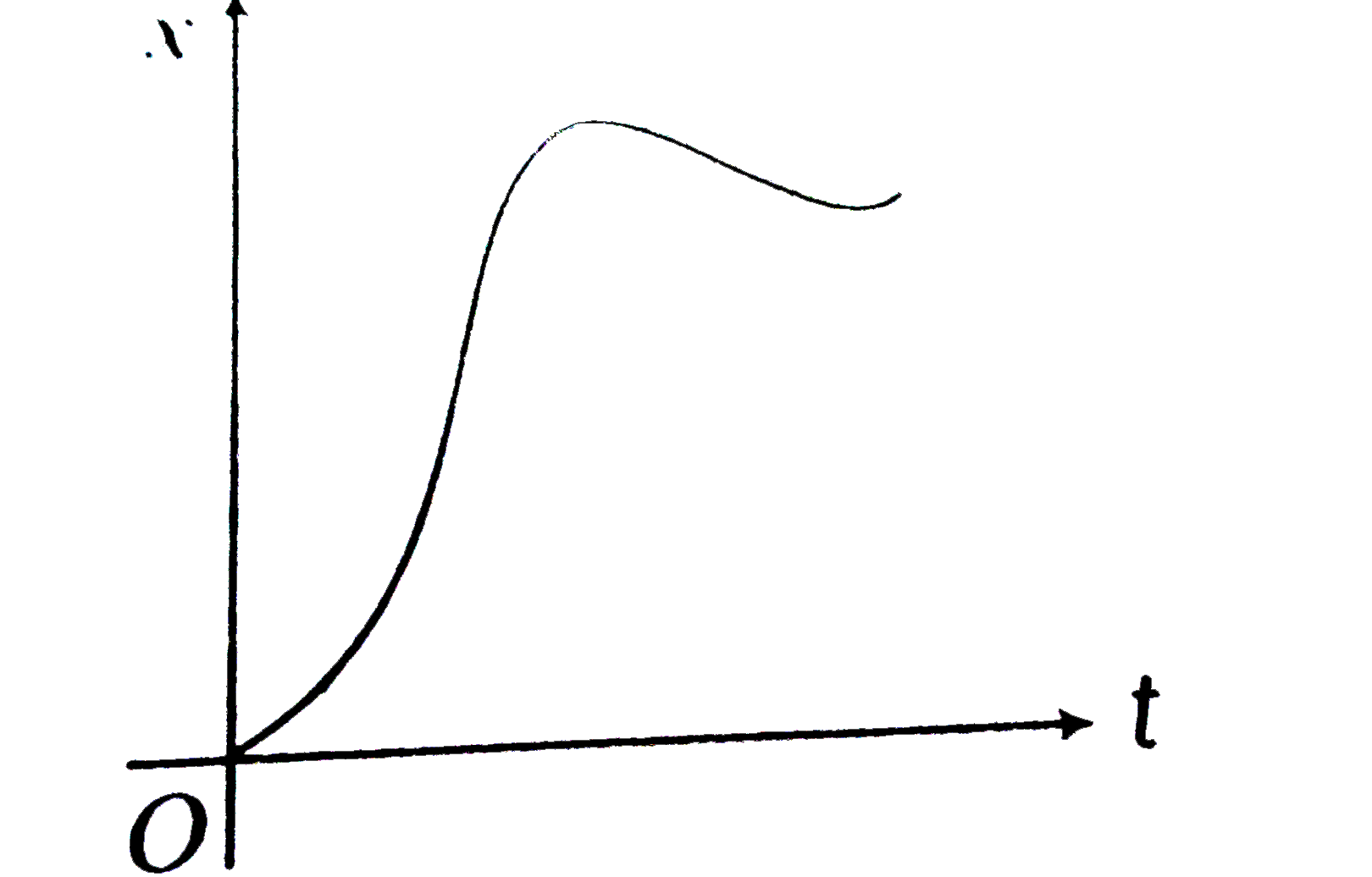
View SolutionThe velocity of body is given as `v = 20 + 0.1 t^2`. The body is undergoing
View SolutionA particle shows distance-time curve as given in this figure. The maximum instantaneous velocity of the particle is around the point.
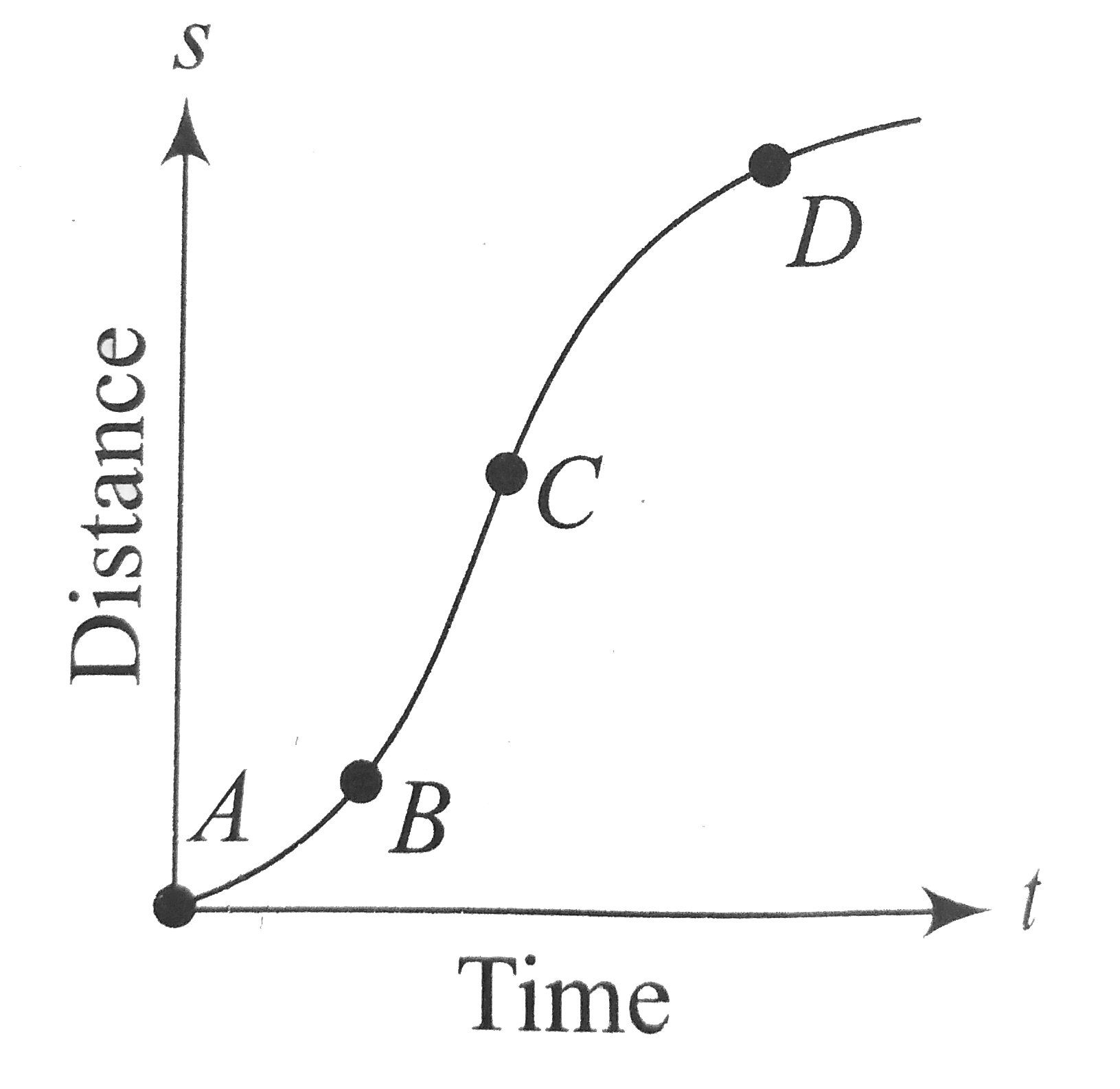 .
.
(a) B (b) C (c) D (d) A
View SolutionThe displacement-time graph of a moving particle is as shown in the figure. The instantaneous velocity of the particle is negative at the point
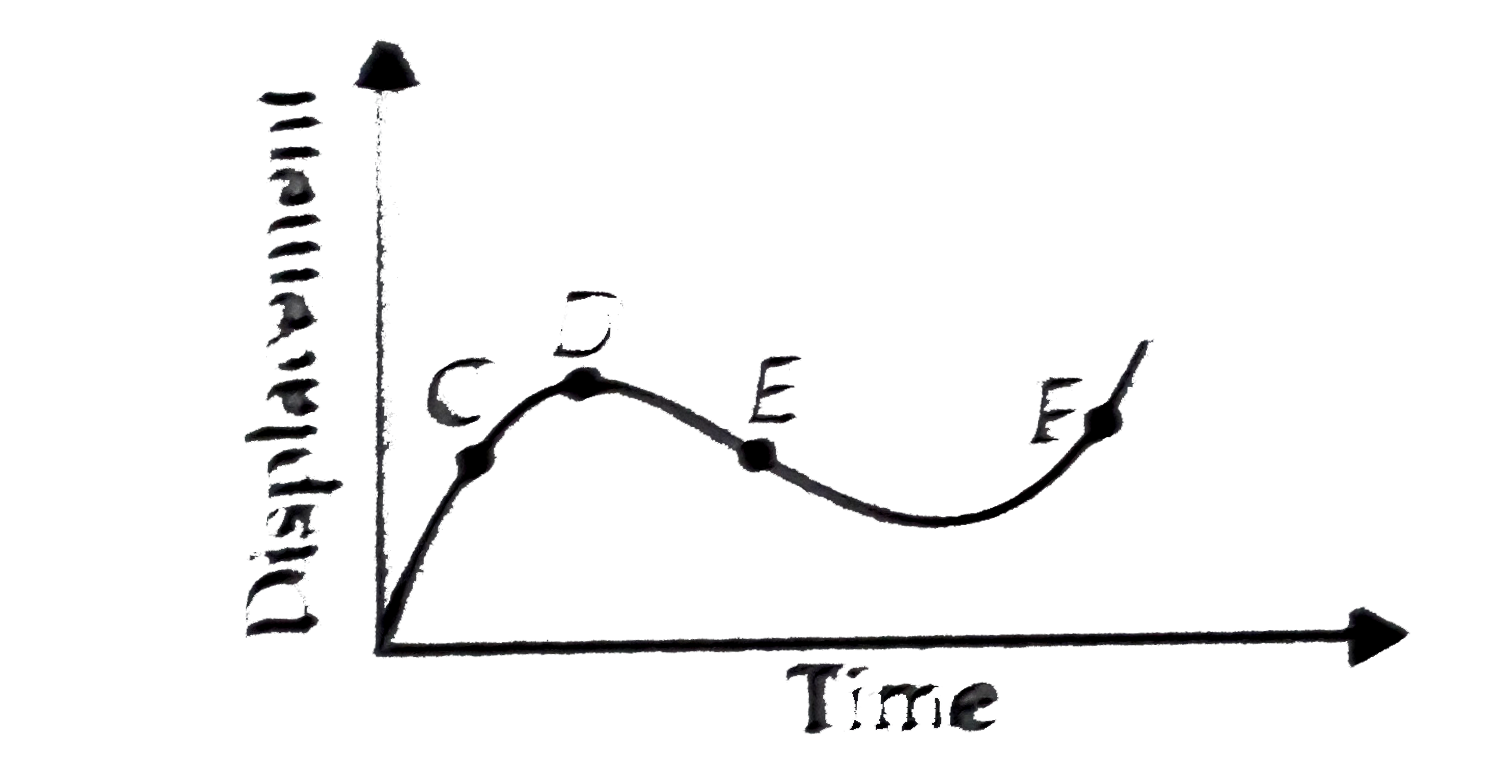
View SolutionThe velocity `upsilon` of a particle as a function of its position (x) is expressed as `upsilon = sqrt(c_(1)-c_(2)x)`, where `c_(1)` and `c_(2)` are positive constants. The acceleration of the particle is
View SolutionA person walks up a stalled 15 m long escalator in 90 s. When standing on the same escalator, now moving, the person is carried up in 60 s. How much time would it take that person to walk up the moving escalator? Does the answer depend on the length of the escalator?
View SolutionA car starts moving along a line, first with acceleration a=5 `ms^(-2)` starting from rest then uniformly and finally decelerating at the same rate a, comes to rest.The total time of motion is `tau=25 s`. The average velocity during the time is equal to lt v gt =72 km/hr.How long does the partial move uniformly ?
View SolutionThe displacement of a particle moving in a straight line depends on time as `x=alpha t^(3)+beta t^(2)+gamma t+delta`. The ratio of initial acceleration to its initial velocity depends
View SolutionA starts from rest, with uniform acceleration a. The acceleration of the body as function of time t is given by the equation a = pt, where p is a constant, then the displacement of the particle in the time interval t = 0 to `t=t_(1)` will be
View SolutionA ball is dropped on the floor from a height of 10m. It rebounds to a height of 2.5m. If the ball is in contact with the floor for 0.01sec, the average acceleration during contace is : ` ( g=9.8 m//s ^(2)) `
View SolutionParticle A is moving along X-axis. At time t = 0, it has velocity of `10 ms^(-1)` and acceleration `-4ms^(-2)`. Particle B has velocity of `20 ms^(-1)` and acceleration `-2 ms^(-2)`. Initially both the particles are at origion. At time t = 2 distance between the particles are at origin. At time t = 2 s distance between the particles is
View SolutionAt a metro station, a girl walks up a stationary escalator in time `t_1`. If she remains stationary on the escalator, then the escalator take her up in time `t_2`. The time taken by her to walk up on the moving escalator will be
View SolutionThe displacement of a body along X-axis depends on time as `sqrt(x)=t+1`. Then the velocity of body.
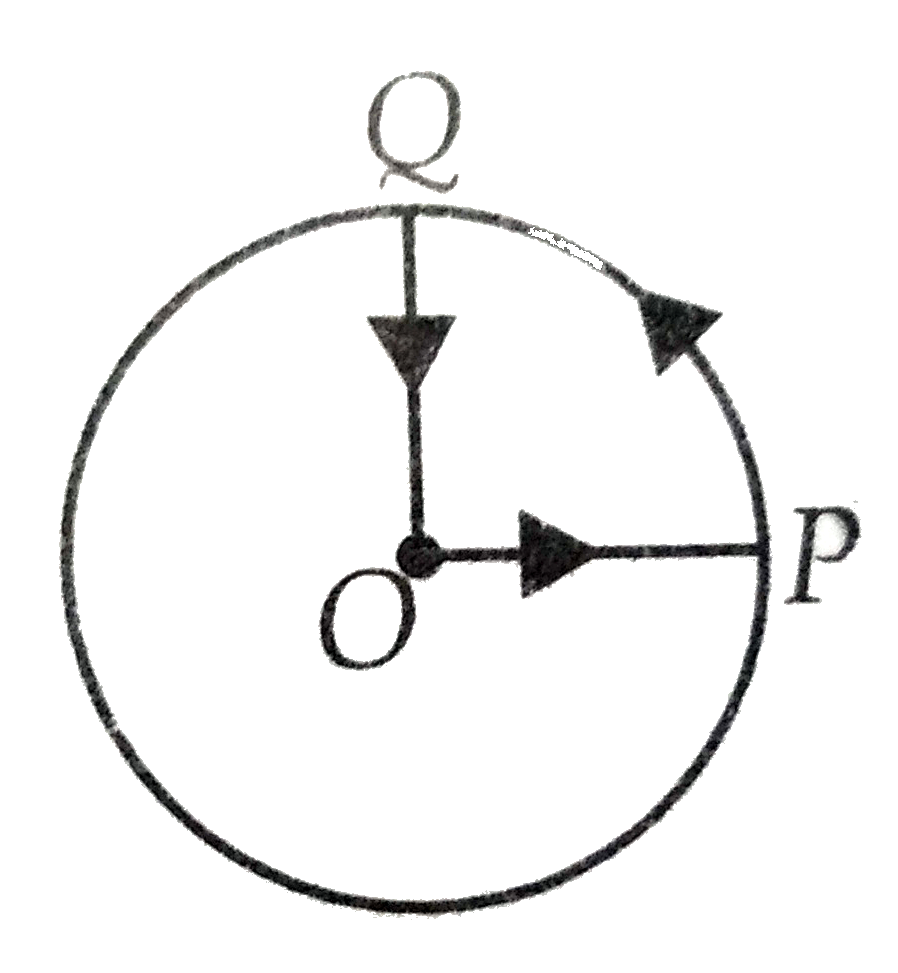
View SolutionA cyclist starts from the centre O of a circular park of radius 1 km. reaches the edge P of the park, then cycles along the circumference and returns to the centre along QO as shown in the figure.
IF the rounds trip takes ten minutes, the net displacement and average speed of the cyclist ( in metre and kilometre per hour) is
View SolutionA particle moves along a straight line OX. At a time t(in second), the distance x (in metre) of the particle from O is given by
`x = 40 + 12t - t^(3)`
How long would the particle travel before coming to rest ?
View SolutionTwo boys are standing at the ends A and B of a ground where AB = a. The boy at B starts running in a direction perpendicular to AB with velocity `v_(1)` . The boy at A starts running simultaneously with velocity v and catches the other in a time t, where t is
View SolutionA bullet emerges from a barrel of length `1.2 m` with a speed of `640 ms^(1)`. Assuming constant acceleration, after the gun is fired is
View SolutionFrom the top of a tower, 80m high from the ground a stone is thrown in the horizontal direction with a velocity of `8 ms^(1)`. The stone reaches the ground after a time t and falls at a distance of d from the foot of the tower. Assuming `g=10ms^(2)`, the time t and distance d are given respectively by
View SolutionA boggy of uniformly moving train is suddenly detached from train and stops after covering some distance. The distance covered by the boggy and distance covered by the train in the same time has relation
View SolutionA man is 45 m behind the bus when the bus starts acceleration from rest with acceleration `2.5(m)/(s^2)`. With what minimum velocity should man start running to catch the bus?
View SolutionA body moves for a total of nine second starting from rest with uniform acceleration and then with uniform retardation, which is twice the value of acceleration and then stop. The duration of uniform acceleration is
View SolutionA point initially at rest moves along x-axis. Its acceleration varies with time as `a = (6t + 5) m//s^(2)`. If it starts from origin, the distance covered in 2 s is:
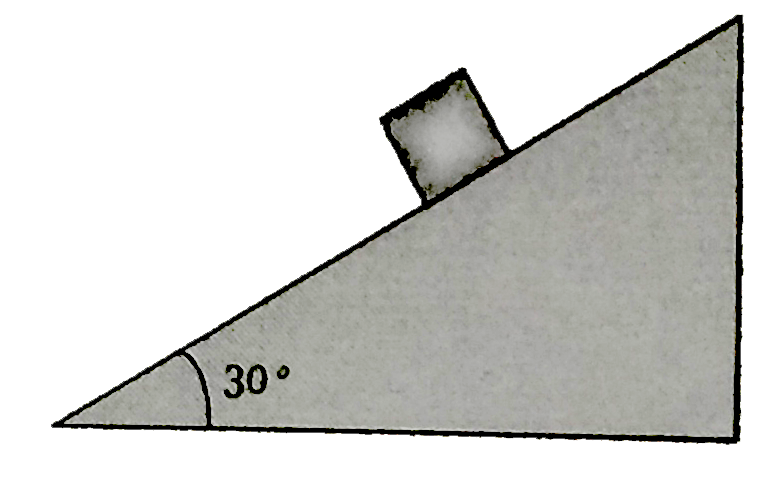
View SolutionThe time taken by a block of wood (initially at rest) to slide down a smooth inclined plane 9.8 m long (angle of inclination is `30^(@)`) is
View SolutionA particle move a distance `x` in time `t` according to equation `x = (t + 5)^-1`. The acceleration of particle is proportional to.
View SolutionA ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View SolutionThe position of a particle along X-axis at time t is given by `x=2+t-3t^(2)`. The displacement and the distance travelled in the interval, t = 0 to t = 1 are respectively
View SolutionA ball falls freely from rest. The ratio of the distance travelled in first, second, third and fourth second is
View SolutionWhat is nature of trajectory of a particle having a uniformly accelerated motion in a plane?
View SolutionA particle moves along a straight line. Its position at any instant is given by `x = 32t-(8t^3)/3` where x is in metres and t in seconds. Find the acceleration of the particle at the instant when particle is at rest.
View SolutionA point moves in a straight line so its displacement `x` meter at time `t` second is given by `x^(2)=1+t^(2)`. Its acceleration in `ms^(-2)` at time `t` second is .
View SolutionThe displacement `x` of a particle varies with time `t` as `x = ae^(-alpha t) + be^(beta t)`. Where `a,b, alpha` and `beta` positive constant.
The velocity of the particle will.
View SolutionGalileo's law of odd number: The distances traversed, during equal intervals of time, by a body falling from rest, stand to one another in the same ratio as the odd number beginning with unity [namelly, `1 : 3 :5 : 7`....]. Prove it.
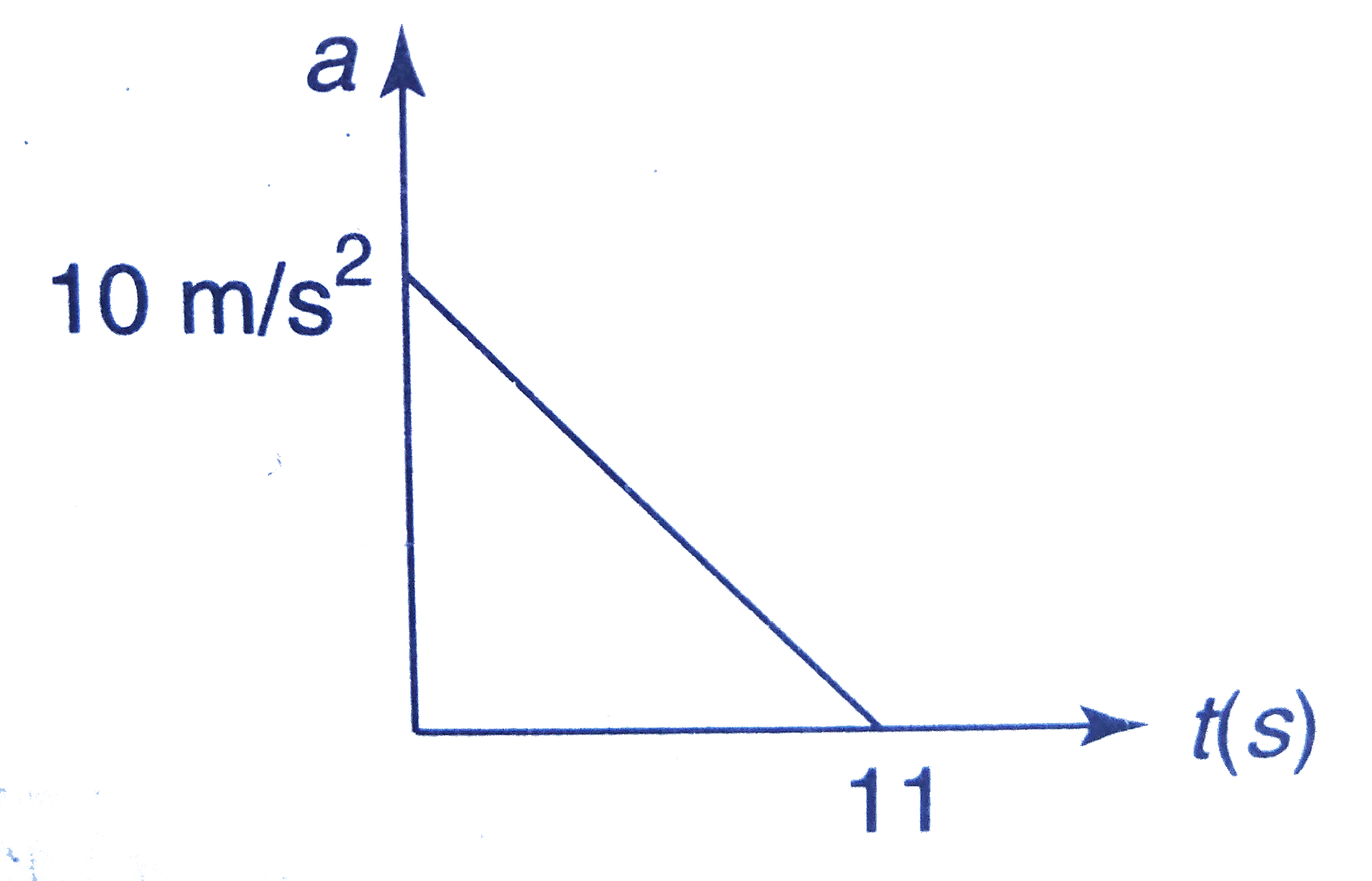
View SolutionA particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.
View SolutionThe acceleration (a)-time(t) graph for a particle moving along a straight from rest is shown in figur. Which of the following graph is the best representation of its velocity (v) with time (t) ?
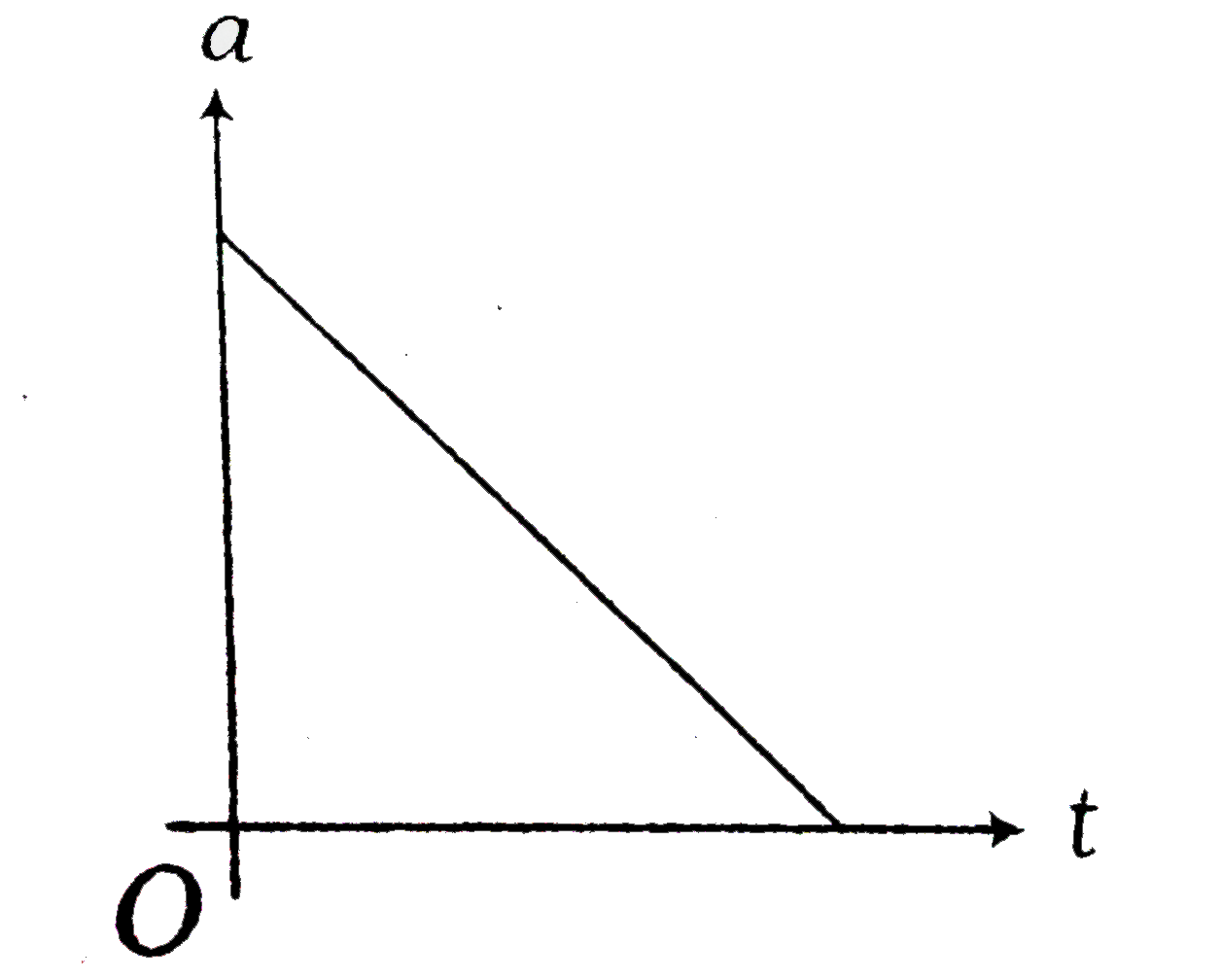
View SolutionA particle moving with uniform acceleration has average velocities `nu_1, nu_2` and `nu_3` over the successive intervals of time `t_1, t_2` and `t_3` respectively. The value of `(nu_1 - nu_2)/(nu_2 - nu_3)` will be
View SolutionThe velocity-time graph for a particle moving along X-axis is shown in the figure. The corresponding displacement-time graph is correctly shown by
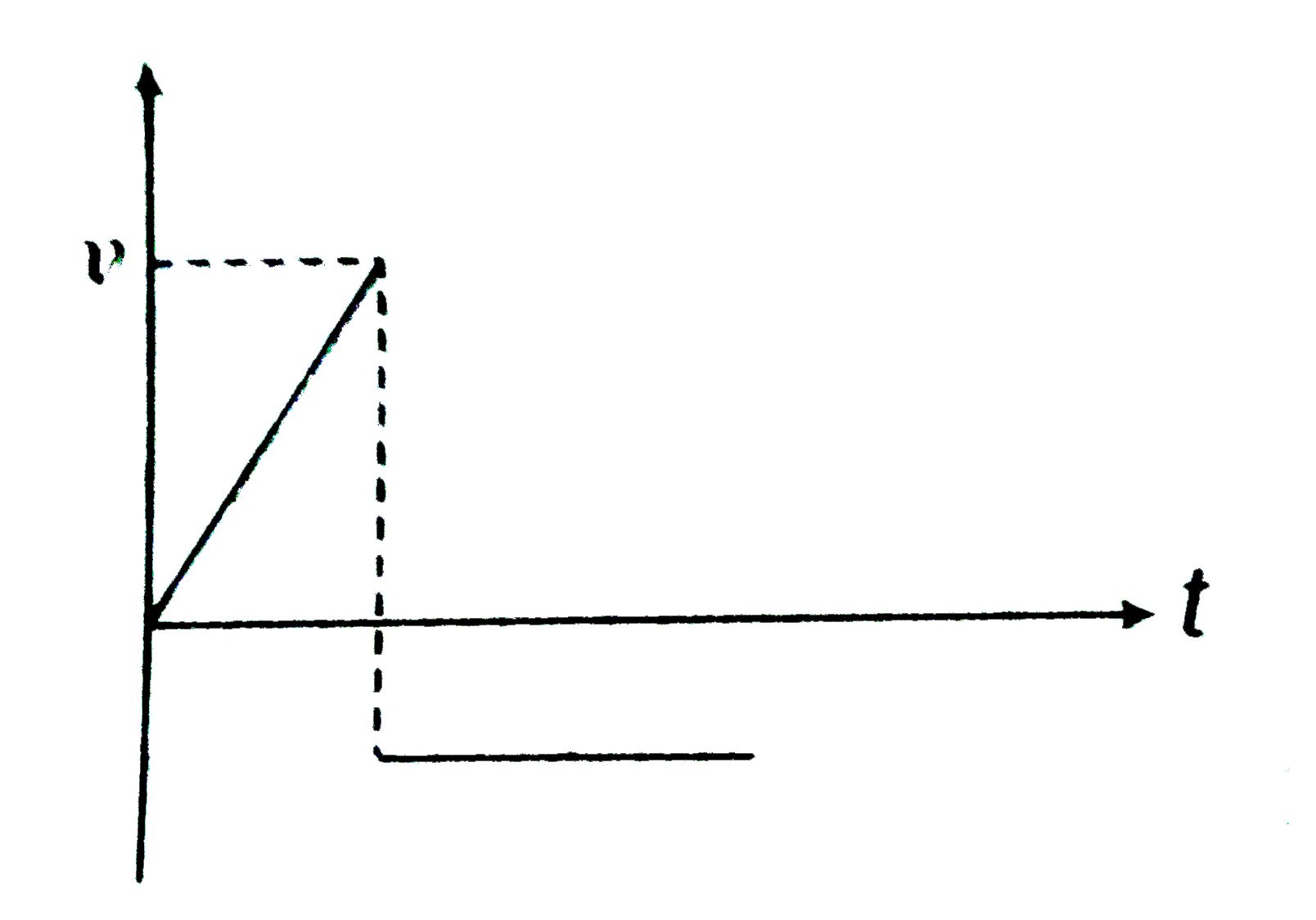
View SolutionThe given graph shows the variation of velocity with displacement. Which one of the graph given below correctly represents the variation of acceleration with displacement :-
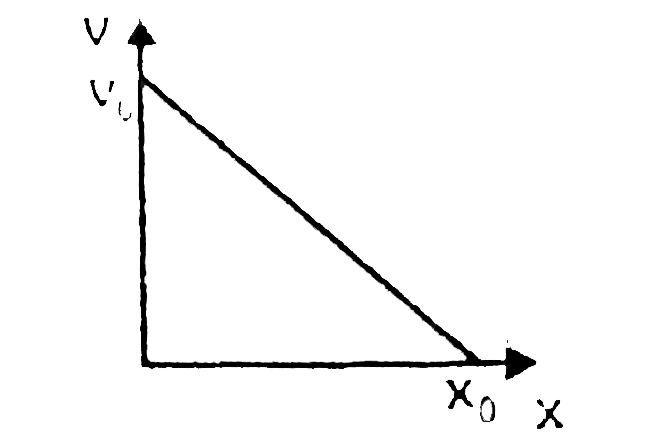
View SolutionThe displacement x of a particle in a straight line motion is given by `x=1-t-t^(2)`. The correct representation of the motion is
View SolutionThe verical of point above the ground is twice that of Q. A particle is projected downward with a speed of `5 ms^(-1)` from P and at the same time another particle is projected upward with the same speed from W. Both particle reach the ground simultaneously, then
View SolutionAmong the four graphs, there is only one graph for which average velocity over the time interval (0, T) can vanish for a suitably chosen T. Which one is it?
View SolutionA lift is coming from `8th` floor and is just about to reach `4th` floor. Taking ground floor as origin and positive direction upwards for all quantities, which one of the following is correct ?
View SolutionIn one dimensional motion, instantaneous speed `v` satisfies `(0 le v lt v_0)` then
View SolutionThe displacement of a particle is moving by `x = (t - 2)^2` where `x` is in metres and `t` in second. The distance covered by the particle in first `4` seconds is.
View SolutionA driver having a definite reaction time is capable of stopping his car over a distance of 30 m on seeing a red traffic signal, when the speed of the car is 72 km/hr andover a distance of 10 m when the speed is 36 km/hr. Find the distance over which he can stop the car if it were running at a speed of 54 km/hr. Assume that his reaction time and the deceleration of the car remains same in all the three cases.
View SolutionThe velocity `(upsilon)` of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
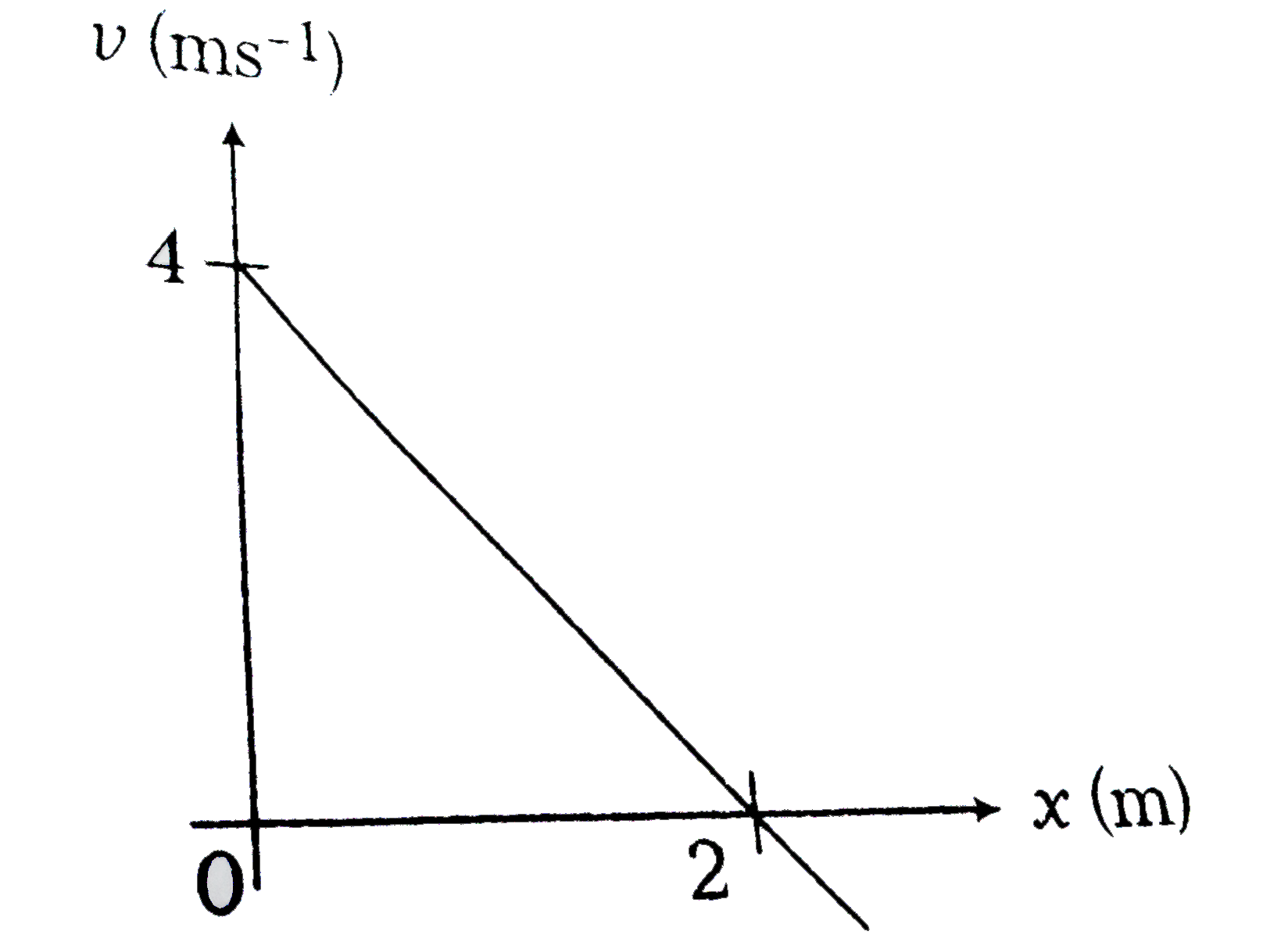
View SolutionA car A moves along north with velocity 30 km/h and another car B moves along east with velocity 40 km/h. The relative velocity of A with respect to B is
View SolutionRain is falling vertically downward with velocity `4m//s.` A man is moving horizontally with velocity `3 m//s`, the velocity of rain with respect to man is
View SolutionA ship is travelling due east at a speed of `15 km//h.` Find the speed of a boat heading `30^@` east of north if it appears always due north from the ship.
View SolutionA man takes `3 h` to cover a certain distance along the flow and takes `6h` to cover the same distance opposite to flow. In how much time, he will cross this distance in still water.
View SolutionA river `500m` wide is flowing at a rate of `4 m//s.` A boat is sailing at a velocity of `10 m//s` with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
View SolutionA ball is dropped vertically from a height d above the ground. It hits the ground and bounces up vertically to a height d/2. Neglecting subsequent motion and air resistance, its velocity v varies with the heiht h above the ground as
View SolutionThe driver of a train moving at a speed ` v_(1)` sights another train at a disane ` d`, ahead of him moving in the same direction with a slower speed ` v_(2)`. He applies the brakes and gives a constant teradation ` a` to his train. Show that here will be no collision if ` d gt (v_(1) -v_(2))^(2) //2 a`.
View SolutionThe width of river is 1 km. The velocity of boat is 5 km/hr. The boat covered the width of river with shortest possible path in 15 min. Then the velocity of river stream is:
View Solution
View SolutionWater drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. `(g = 10 ms^-2)`
View SolutionA man in a lift ascending with an upward acceleration `a` throws a ball vertically upwards with a velocity `v` with respect to himself and catches it after `t_1` seconds. After wards when the lift is descending with the same acceleration `a` acting downwards the man again throws the ball vertically upwards with the same velocity with respect to him and catches it after `t_2` seconds?
View SolutionA particle moving along x-axis has acceleration f, at time t, given by `f = f_(0) (1-(t)/(T))`, where `f_(0)` and T are constants. The particle at `t = 0` has zero velocity. In the time interval between `t = 0` and the instant when `f = 0`, the particle's velocity `(v_(x))` is
View SolutionThe position x of a particle w.r.t. time t along x-axis is given by a `x = 9 t^(2)-t^(3)`, where x is in metre and t in sec. What will be the position of this particle when it achieves maximum speed along the +x direction ?
View SolutionTwo particles `P` and `Q` simulaneously start moving from point `A` with velocities `15m//s` and `20m//s` respectively. The two particles move with acceleration equal in magnitude but opposite in direction. When `P` overtakes `Q` at `B` then its velocity is `30m//s`. Find velocity of `Q` at point `B` ( in m/s).
View SolutionA body dropped from top of a tower falls through ` 40 m` during the last two seconds of its fall. The height of tower in m is ( g= 10 m//s^2)`
View SolutionA small block slides without friction down an iclined plane starting form rest. Let `S_(n)` be the distance traveled from time `t = n - 1` to `t = n`. Then `(S_(n))/(S_(n + 1))` is:
View SolutionA particle located at `x = 0` at time `t = 0`, starts moving along with the positive x-direction with a velocity v that varies as ` v = alpha sqrt(x)`. The displacement of the particle varies with time as
View SolutionA body falls freely from the top of a tower. It covers 36% of the total height in the lkast second before striking the ground level. The height of the tower is
View SolutionAn elevator car whose floor to ceiling distance is equal to `2.7 m` starts ascending with constant acceleration `1.2 m//s^(2)`, 2 sec after the start a bolt begins falling from the ceiling of the car. Answer the following question `(g=9.8 m//s^(2))`
The bolt's free fall time is
View Solution
(A) Taking it together questions and complete solutions for chapter MOTION IN A PLANE of DC PANDEY ENGLISH of Class 11