Complete Solutions to Level 2 Multiple Correct of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| DC PANDEY | Level 2 Multiple Correct |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
A thin hollow sphere of mass `m` is completely filled with non viscous liquid of mass `m`. When the sphere roll-on horizontal ground such that centre moves with velocity `v`, kinetic enerrgy of the system is equal to
View SolutionA solid uniform disc of mass `m` rols without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
View SolutionA uniform slender rod of mass `m` and length `L` is released from rest, with its lower end touching a frictionaless horizontal floor. At the initial moment, the rod is inclined at an angle `theta=30^(@)` with the vertical. Thent he value of normal reaction from the from the floor just after release will be
View SolutionA uniform slender rod of mass m and length L is released from rest, with its lower end touching a frictionaless horizontal floor. At the initial moment, the rod is inclined at an angle θ=30∘ with the vertical. Thent he value of normal reaction from the from the floor just after release will be 4mg /7 In the above problem, the initial acceleration of the lower end of the rod will be
View SolutionA disc of radius `R` is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity ad acceleration vectors of point `P` is

View SolutionA straight rod AB of mass `M` and length `L` is placed on a frictionless horizontal surface. A force having constant magnitude F and a fixed direction start acting at the end A. The rod is initially perpendicular to the force. The initial acceleration of end B is
View SolutionA particle mass parallel to x-axis with constant velocity `v` as shown in the figure. The angular velocity of the particle about the origin O

View SolutionA thin uniform rod mass `M` and length `L` is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance `L//3` from the hinge point, when the rod become vertical will
View Solution
A uniform rod AB of length `L` and mass `m` is suspended freely at A and hangs vertically at rest when a particle of same mass `m` is fired horizontally with speed `v` to strike the rod at its mid point. If the particle is brought to rest after the impact. Then the impulsive reaction at A is horizontal direction is
View Solution
A child with mass `m` is standing at the edge of a merry go round having moment of inertia `I`, radius `R` and initial angular velocity `omega` as shown in the figure. The child jumps off the edge of the merry go round with tangential velocity `v` with respect to the ground. The new angular velocity of the merry go round is
View Solution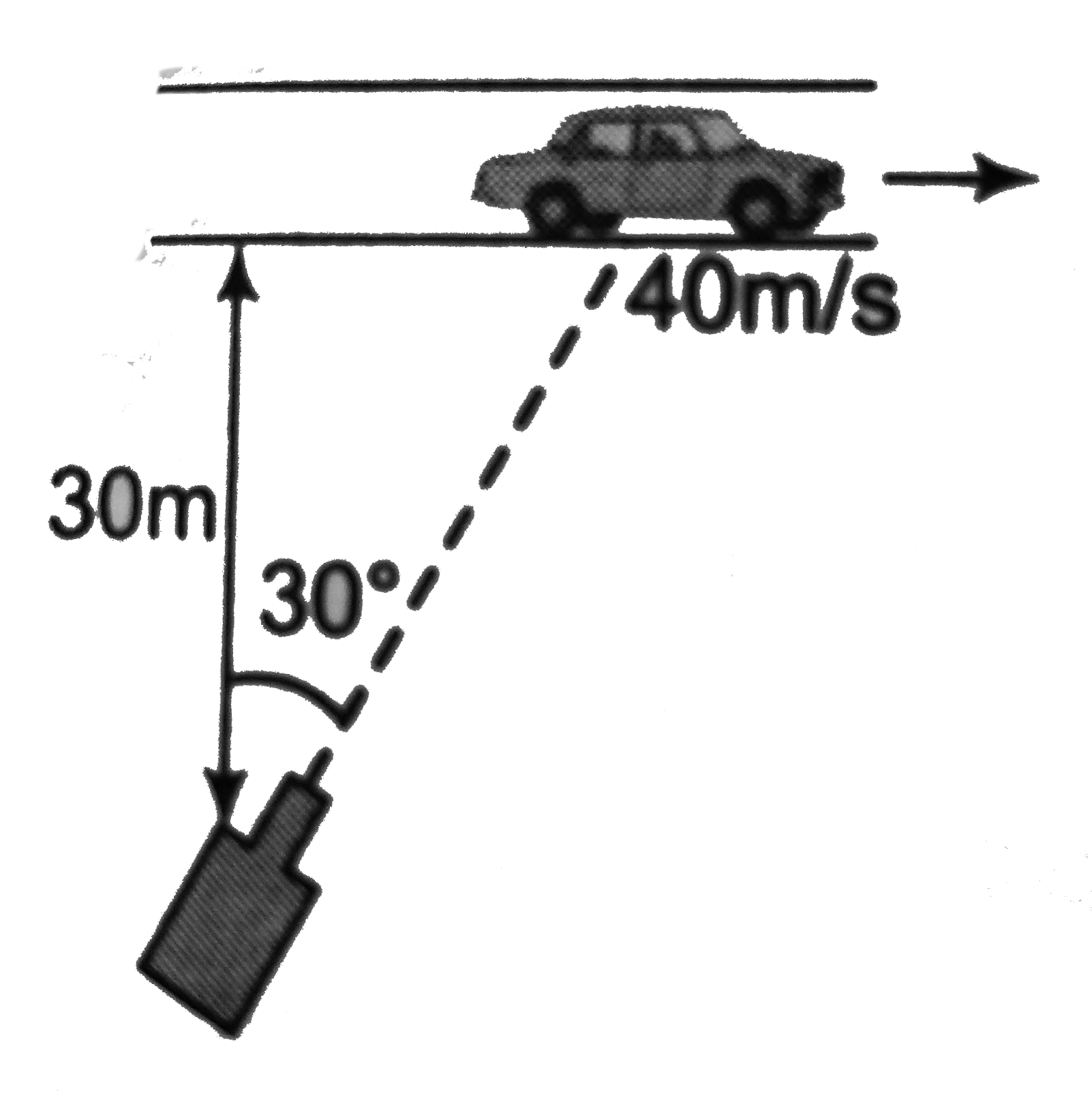
A racing car is travelling along a straight track at a constant velocity of `40m//s`. A fixed TV camera is recording the even as shown in figure. In order to keep the car in view in the position shown the angular velocity of camera should be
View Solution
A uniform rod OA of length `l`, resting on smooth surface is slightly distributed from its vertical position `P` is a point on the rod whose locus is a circle during the subsequent motion of the rod, then the distance OP is equal to
View SolutionA uniform rod OA of length l, resting on smooth surface is slightly distributed from its vertical position P is a point on the rod whose locus is a circle during the subsequent motion of the rod, then the distance OP is equal to 'l/4'. In the above question, the velocity of end O when end A hits the gournd is
View SolutionA uniform rod OA of length l resting on smooth surface slightly disturbed from its vertical position . P is a ipoint on the rod whose locus is a circle during the subsequent motion of the rod. the OP distance is l/4 . In the above question, the velocity of end A at the instant it hits the ground is
View Solution
A solid sphere of mass `m` and radius `R` is gently placed on a conveyer belt moving with constant velocity `v_(0)`. If coefficient of friction between belt and sphere is `2//7` the distance traveled by the centre of the sphere before it starts pure rolling is
View SolutionA mass `m` of radius `r` is rolling horizontally without any slip with a linear speed `v`. It then rolls up to a height given by `(3)/(4)(v^(2))/(g)`
View SolutionFour identical rods each of mass `m` and length `l` are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertia about
View Solution
A uniform circular ring rolls without slipping on a horizontal surface. At any instant, its position is as shown in the figure. Then
View Solution
A cylinder of radius R is to roll without slipping between two planks as shown in the figure. Then
View Solution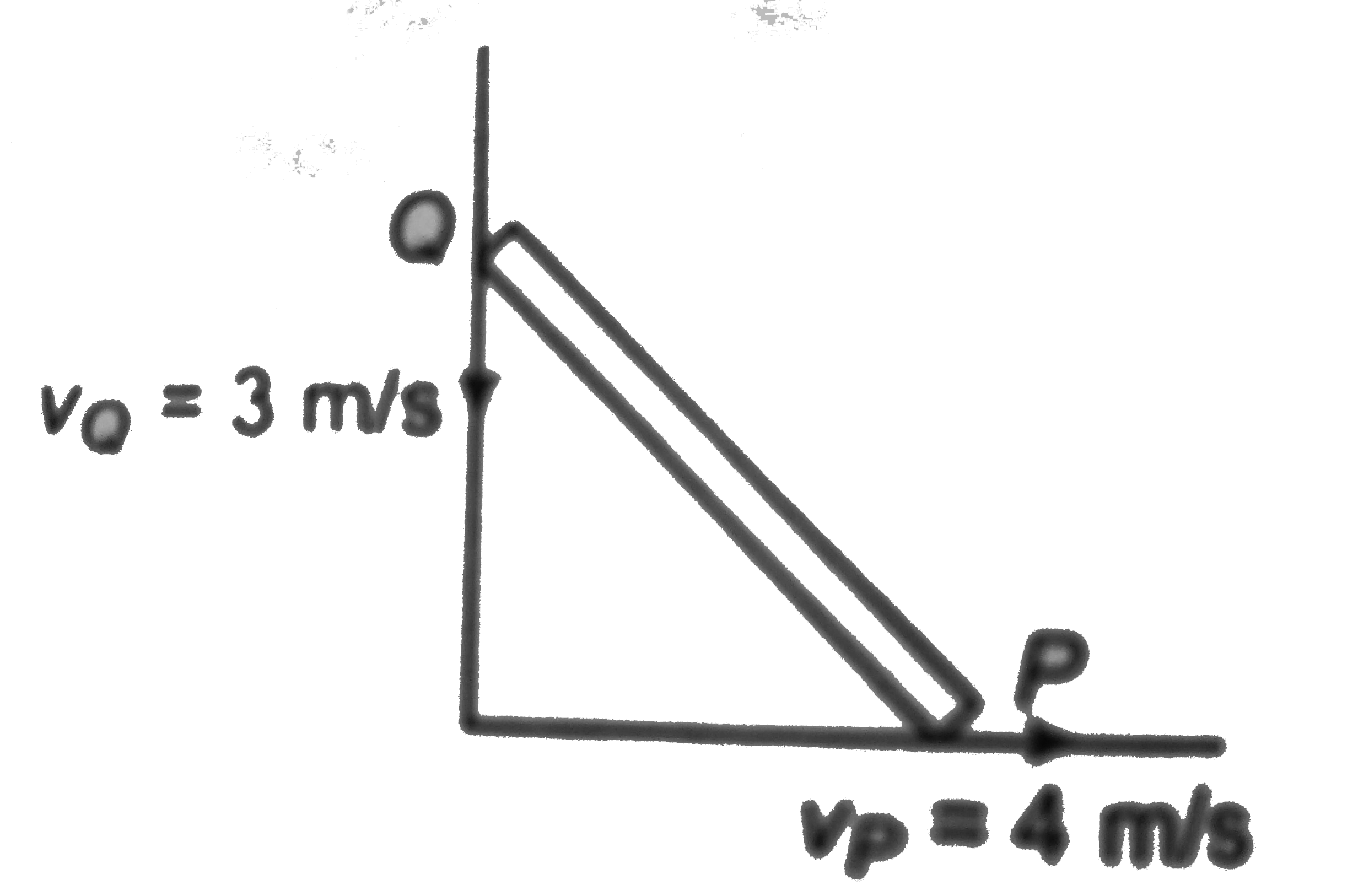
A uniform rod of mass `m=2kg` and length `l=0.5m` is sliding along two mutually perpendicular smooth walls with the two ends P and Q having velocities `U_(P)=4m//s` and `v_(Q)=3m//s` as shown then
View Solution
A wheel is rolling without slipping on a horizontal plane with velocity `v` and acceleration `a` of centre of mass as shown in figure. Acceleration at
View SolutionA uniform rod of length `l` and mass 2 m rests on a smooth horizontal table. A point mass `m` moving horizontally at right angles to the rod with velocity `v` collides with one end of the rod and sticks it. Then
View SolutionA non-uniform ball of radius R and radius of gyration about geometric centre `=R//2` is kept on a frictionless surface. The geometric centre coincides with the centre of mass. The ball is struck horizontally with a sharp impulse `=J` the point of application of the impulse is at a height `h` above the surface. then.
View SolutionA hollow spherical ball is given an initial push, up an incline of inclination angle `alpha`. The ball rolls purely coefficient of static friction between ball and incline `=mu`. During its upwards journey.
View SolutionA uniform disc of mass `m` and radius `R` rotates about a fixed vertical axis passing through its centre with angular velocity `omega`. A particle of same mass `m` and having velocity of `2omegaR` towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View Solution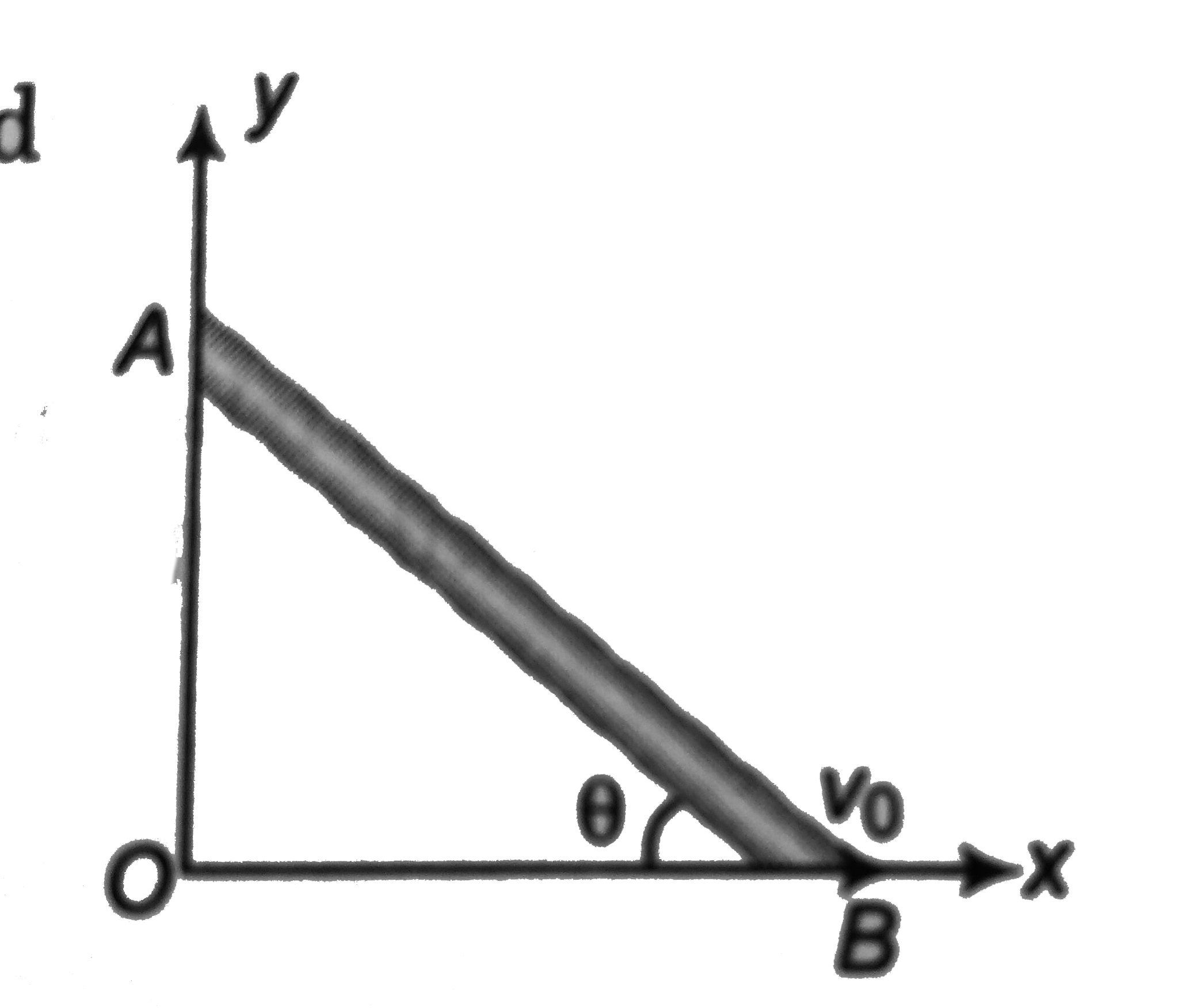
The end B of the rod AB which makes angle `theta` with the floor is being pulled with a constant velocity `v_(v)` as shown. The length of the rod is `l`.
View Solution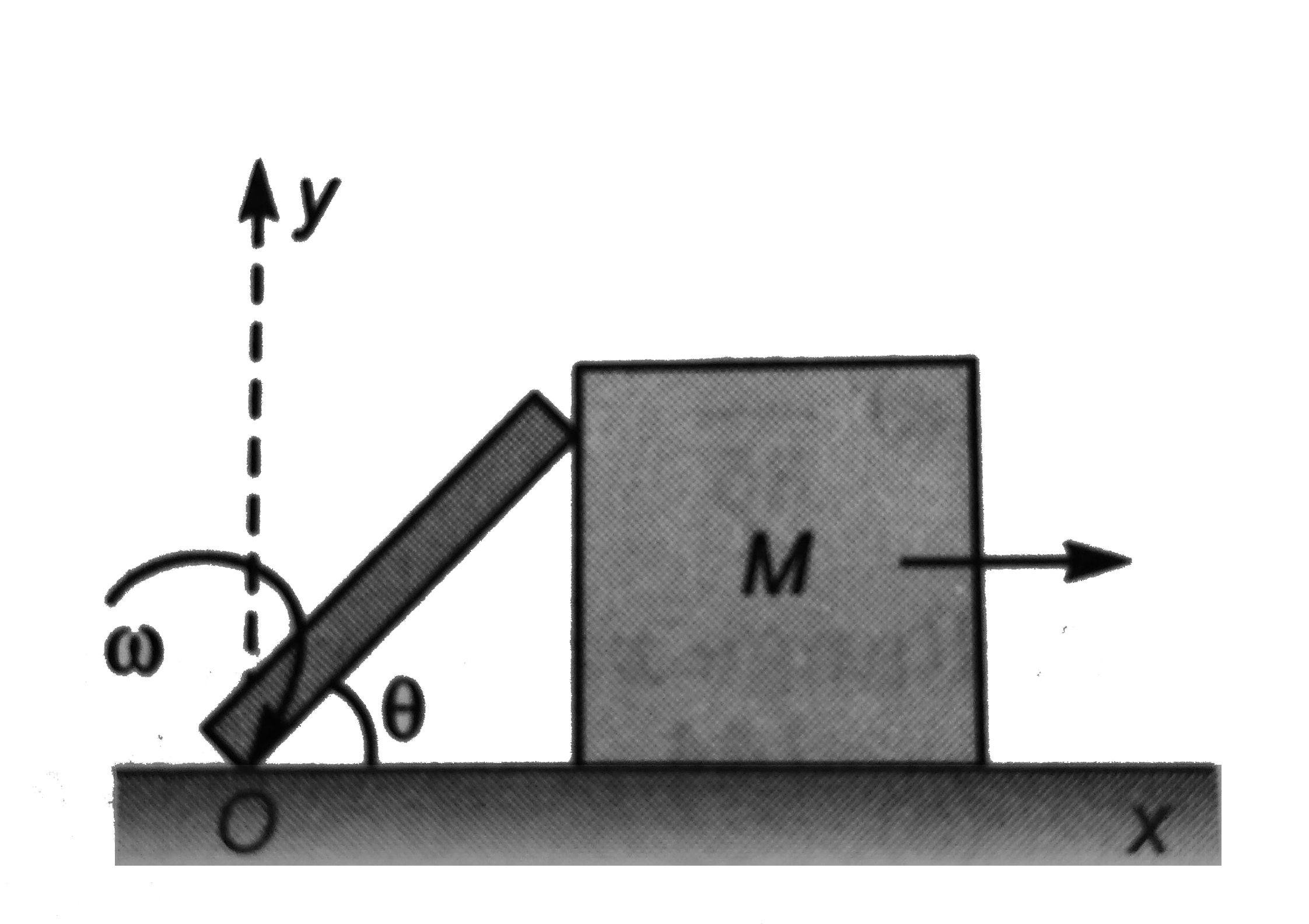
A uniform rod of mass `m` and length `l` is applied pivoted at point `O`. The rod is initially in vertical position and touching a block of mass `M` which is at rest on a horizontal surface. The rod is given a slight jerk and it starts rotating about point `O` this causes the block to move forward as shown The rod loses contact with the block at `theta=30^(@)` all surfaces are smooth now answer the following questions.
Q. The value of ratio `M//m` is a) 2:3 b) 3:2 c) 4:3 d) 3:4
View Solution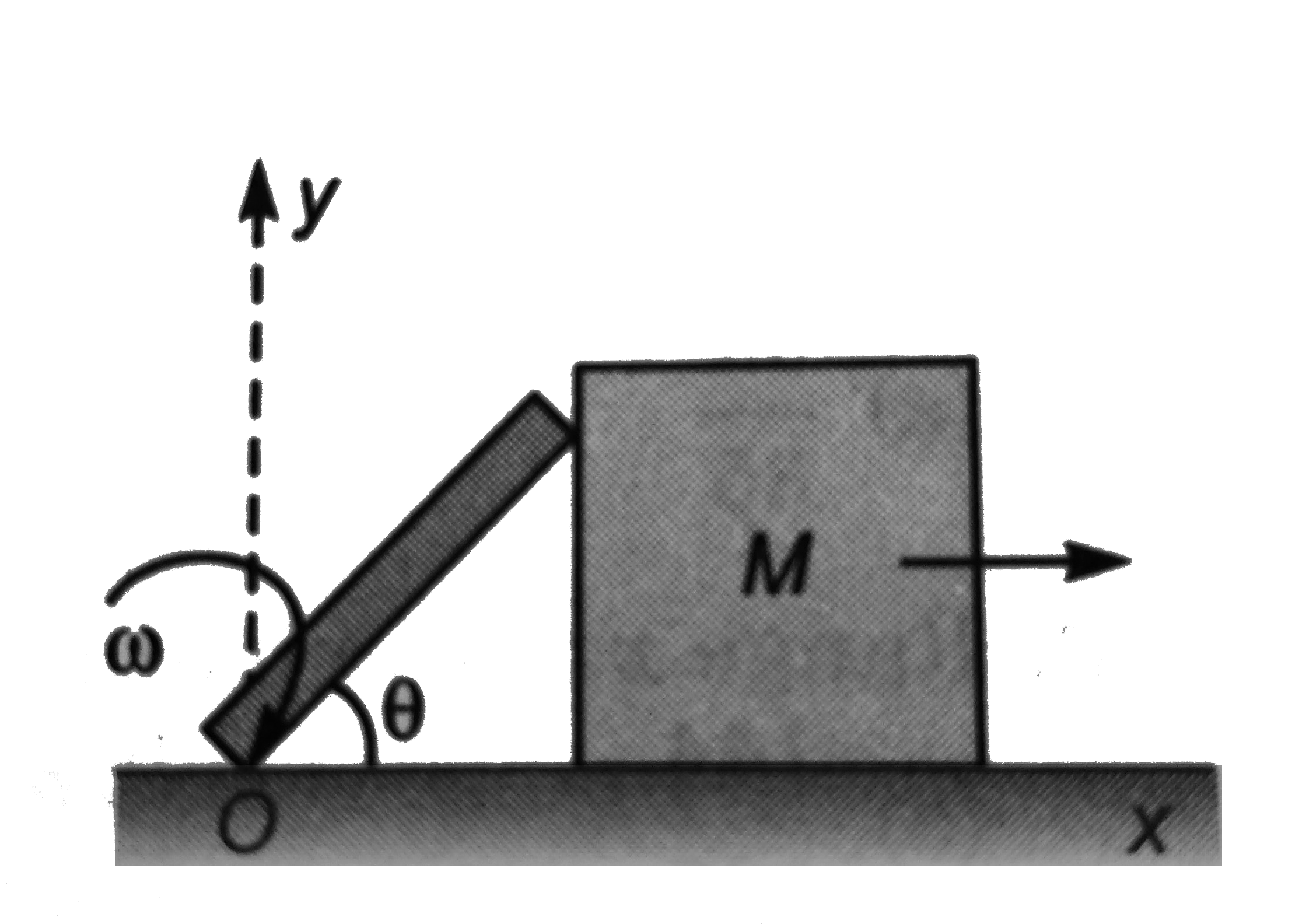
A uniform rod of mass `m` and length `l` is applied pivoted at point `O`. The rod is initially in vertical position and touching a block of mass `M` which is at rest on a horizontal surface. The rod is given a slight jerk and it starts rotating about point `O` this causes the block to move forward as shown The rod loses contact with the block at `theta=30^(@)` all surfaces are smooth now answer the following questions.
Q. The velocity of block when the rod loses contact with the block is
View Solution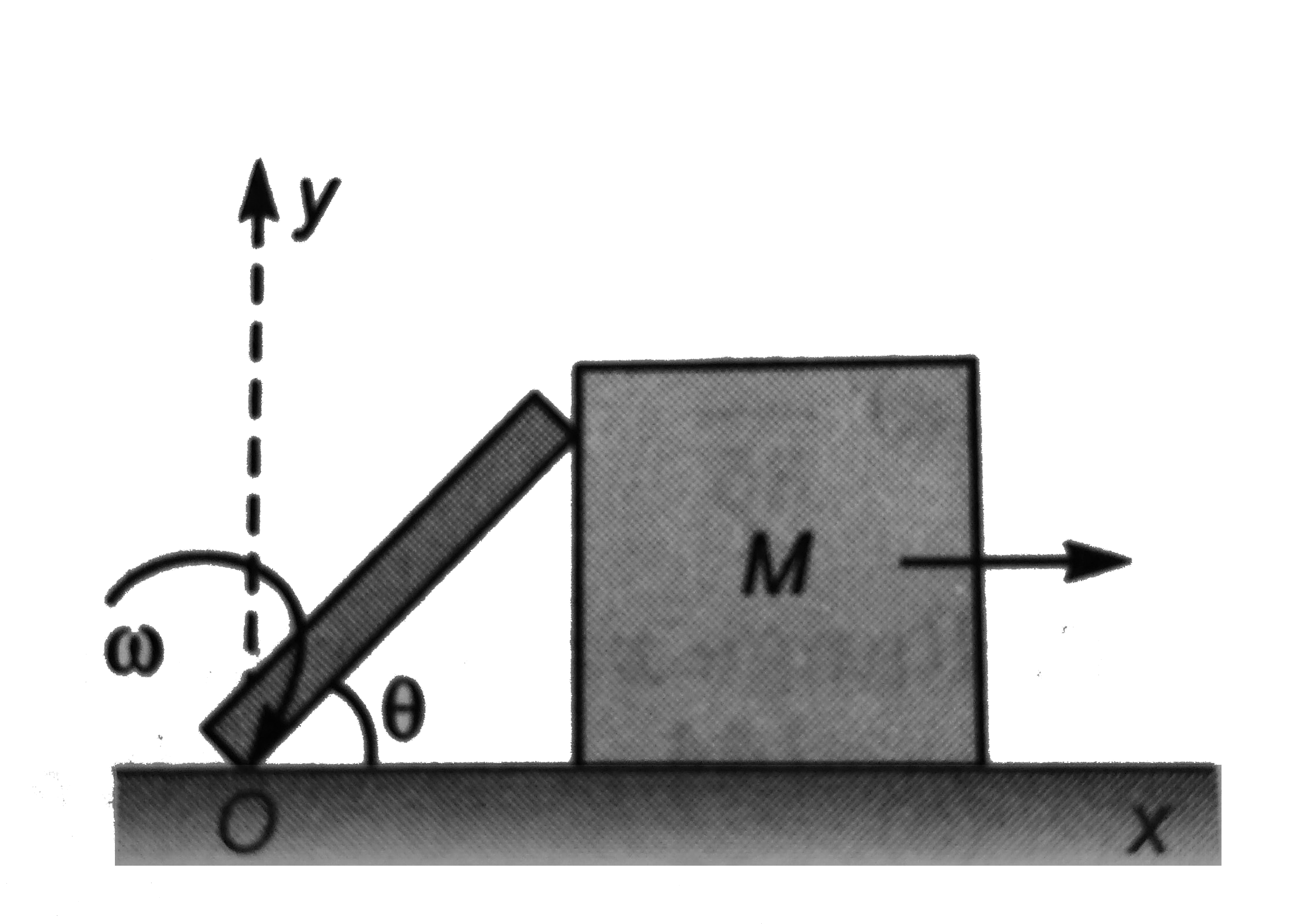
A uniform rod of mass `m` and length `l` is applied pivoted at point `O`. The rod is initially in vertical position and touching a block of mass `M` which is at rest on a horizontal surface. The rod is given a slight jerk and it starts rotating about point `O` this causes the block to move forward as shown The rod loses contact with the block at `theta=30^(@)` all surfaces are smooth now answer the following questions.
Q. The acceleration of centre of mass of rod, when it loses contact with the block is
View Solution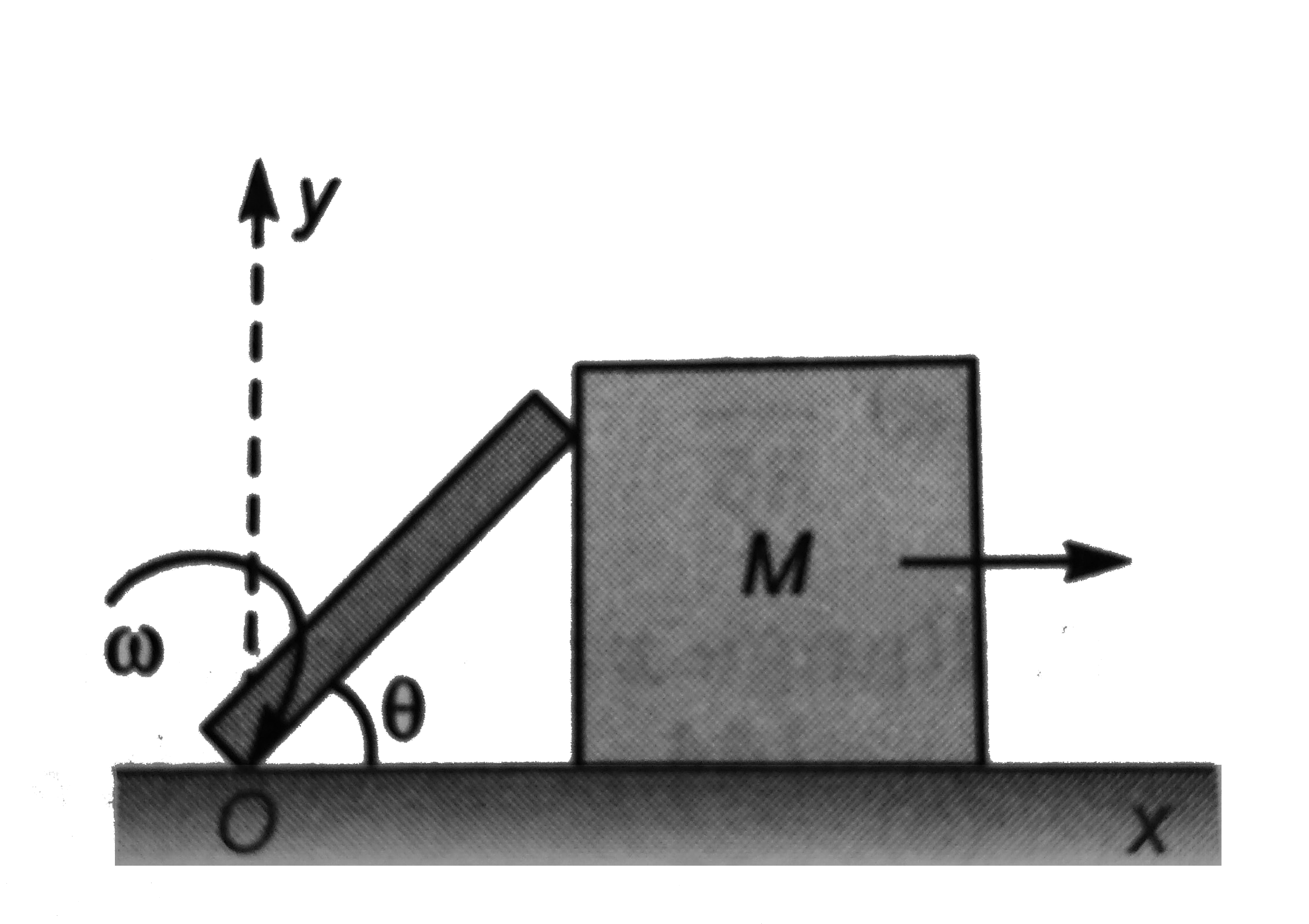
A uniform rod of mass `m` and length `l` is applied pivoted at point `O`. The rod is initially in vertical position and touching a block of mass `M` which is at rest on a horizontal surface. The rod is given a slight jerk and it starts rotating about point `O` this causes the block to move forward as shown The rod loses contact with the block at `theta=30^(@)` all surfaces are smooth now answer the following questions.
Q. The hinge reaction at `O` on the rod when it loses contact with the block is
View SolutionConsider a uniform disc of mass `m`, radius `r` rolling without slipping on a rough surface with linear acceleration `a` and angular acceleration `alpha` due to an external force F as shown in the figure coefficient of friction is `mu`.
Q. The work done by the frictional force at the instant of pure rolling is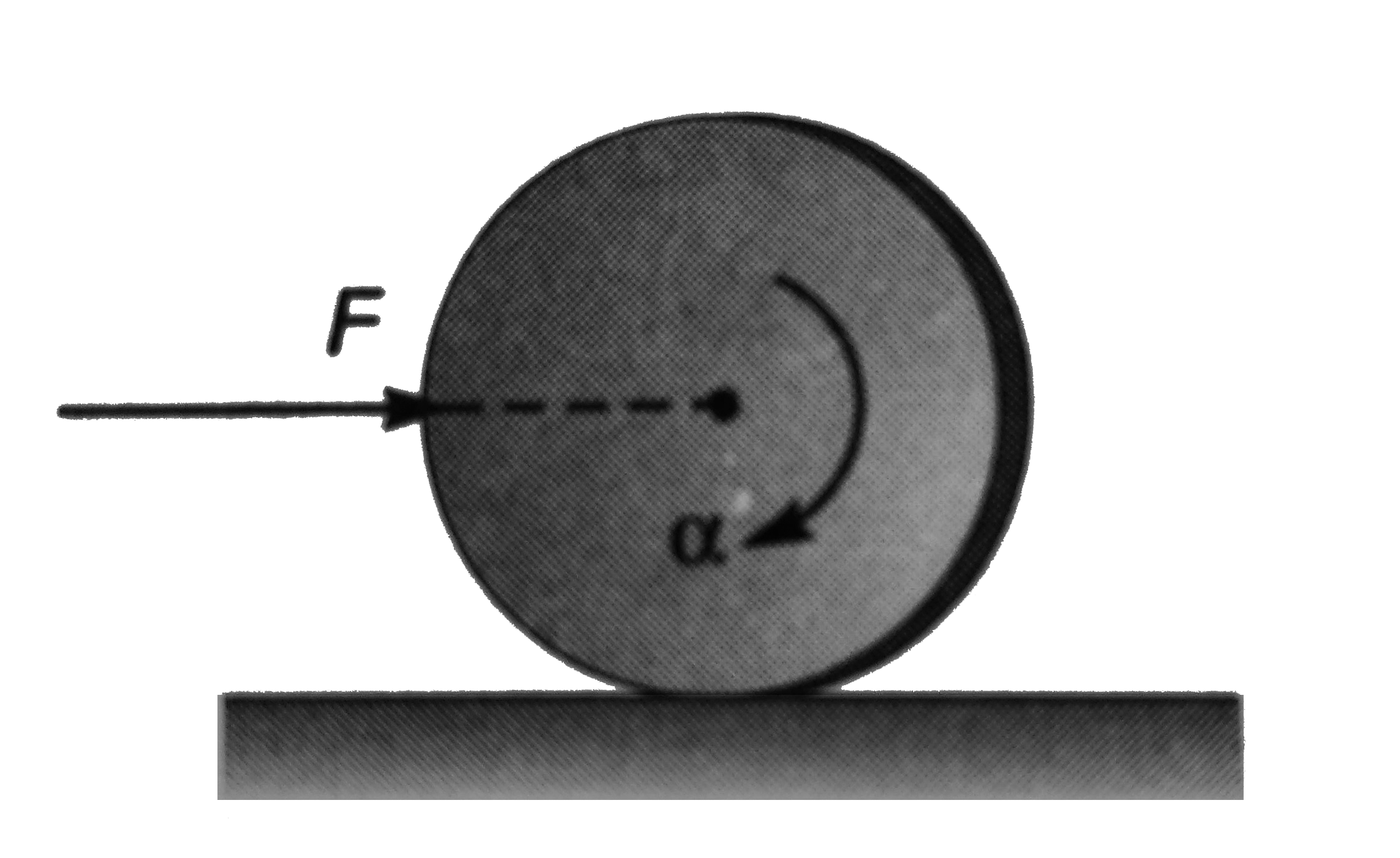
View Solution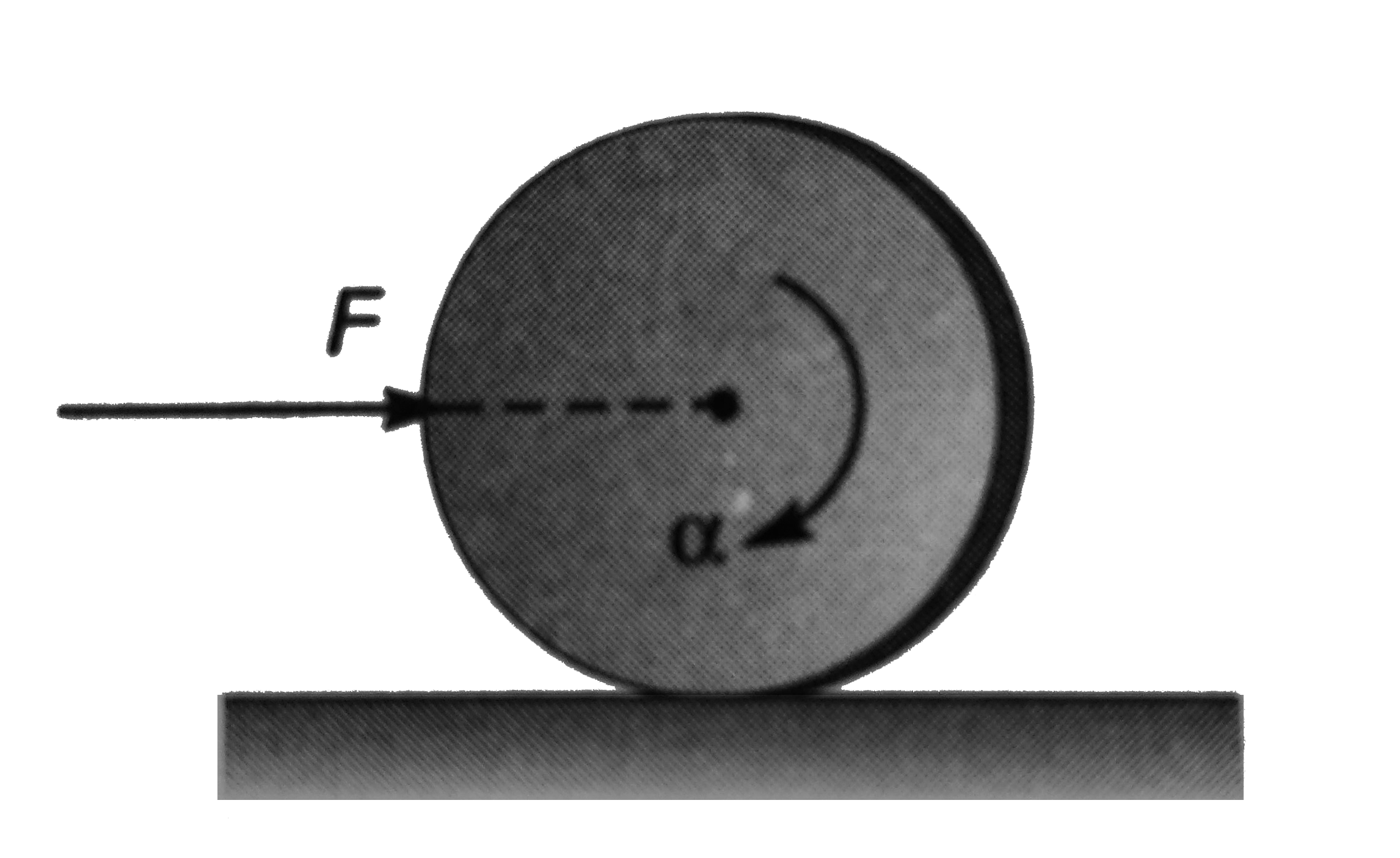
Consider a uniform disc of mass `m`, radius `r` rolling without slipping on a rough surface with linear acceleration `a` and angular acceleration `alpha` due to an external force F as shown in the figure coefficient of friction is `mu`.
Q. The magnitude of frictional force acting on the disc is
View Solution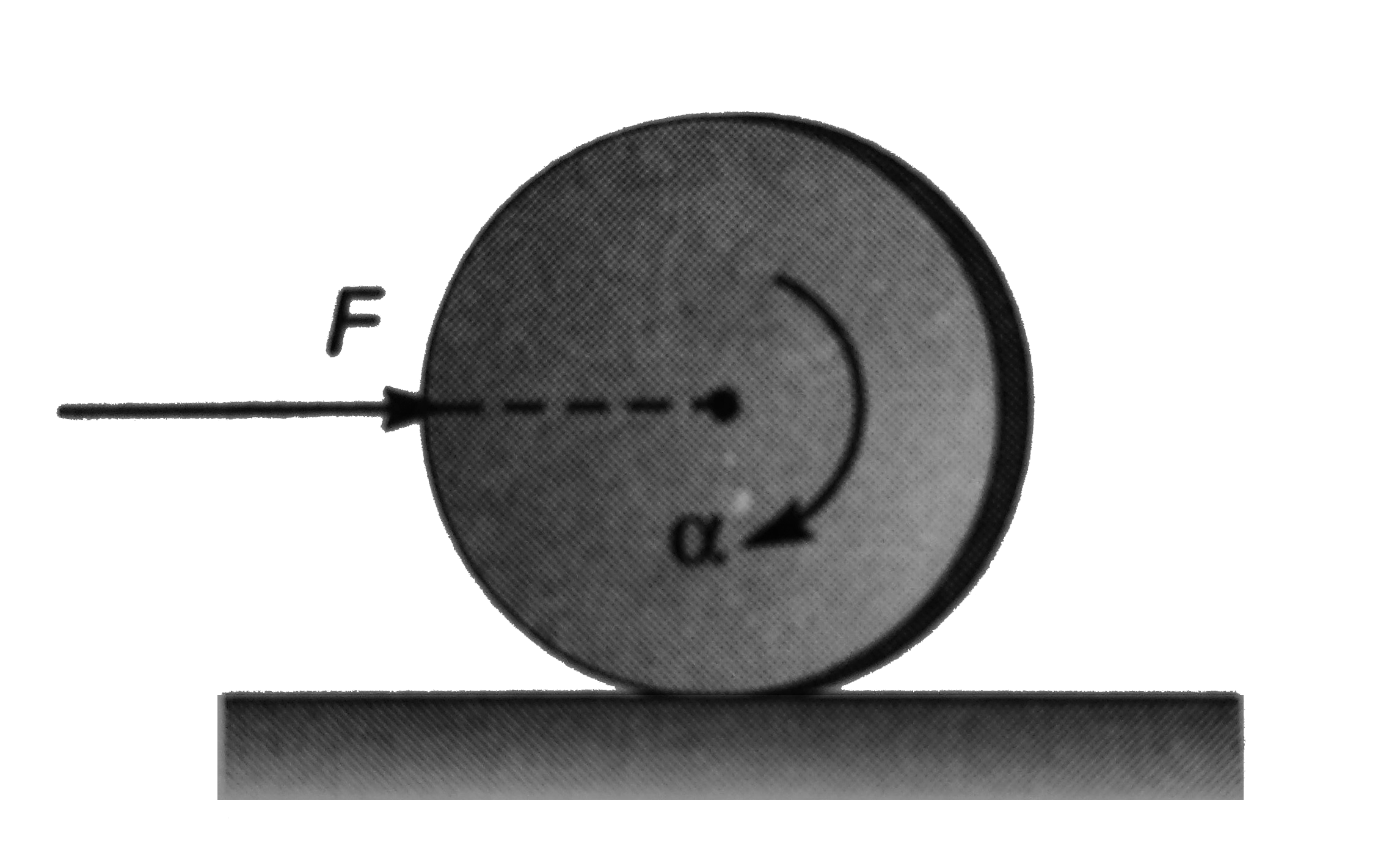
Consider a uniform disc of mass `m`, radius `r` rolling without slipping on a rough surface with linear acceleration `a` and angular acceleration `alpha` due to an external force F as shown in the figure coefficient of friction is `mu`.
Q. Angular momentum of the disc will be conserved about
View Solution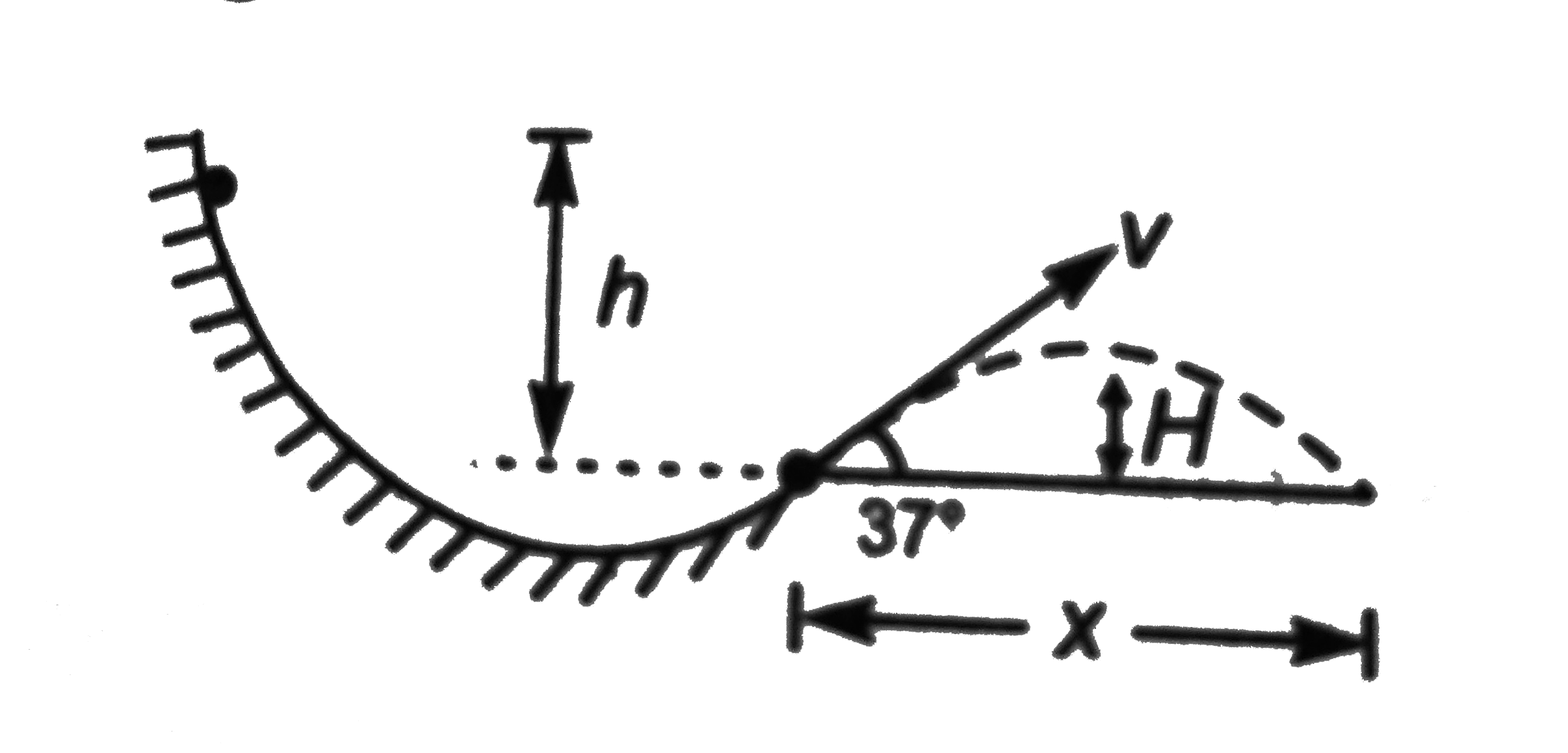
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of `37^(@)` with respect to the ground treat the ball as a thin-walled spherical shell.
Q. The velocity of projection `v` is
View Solution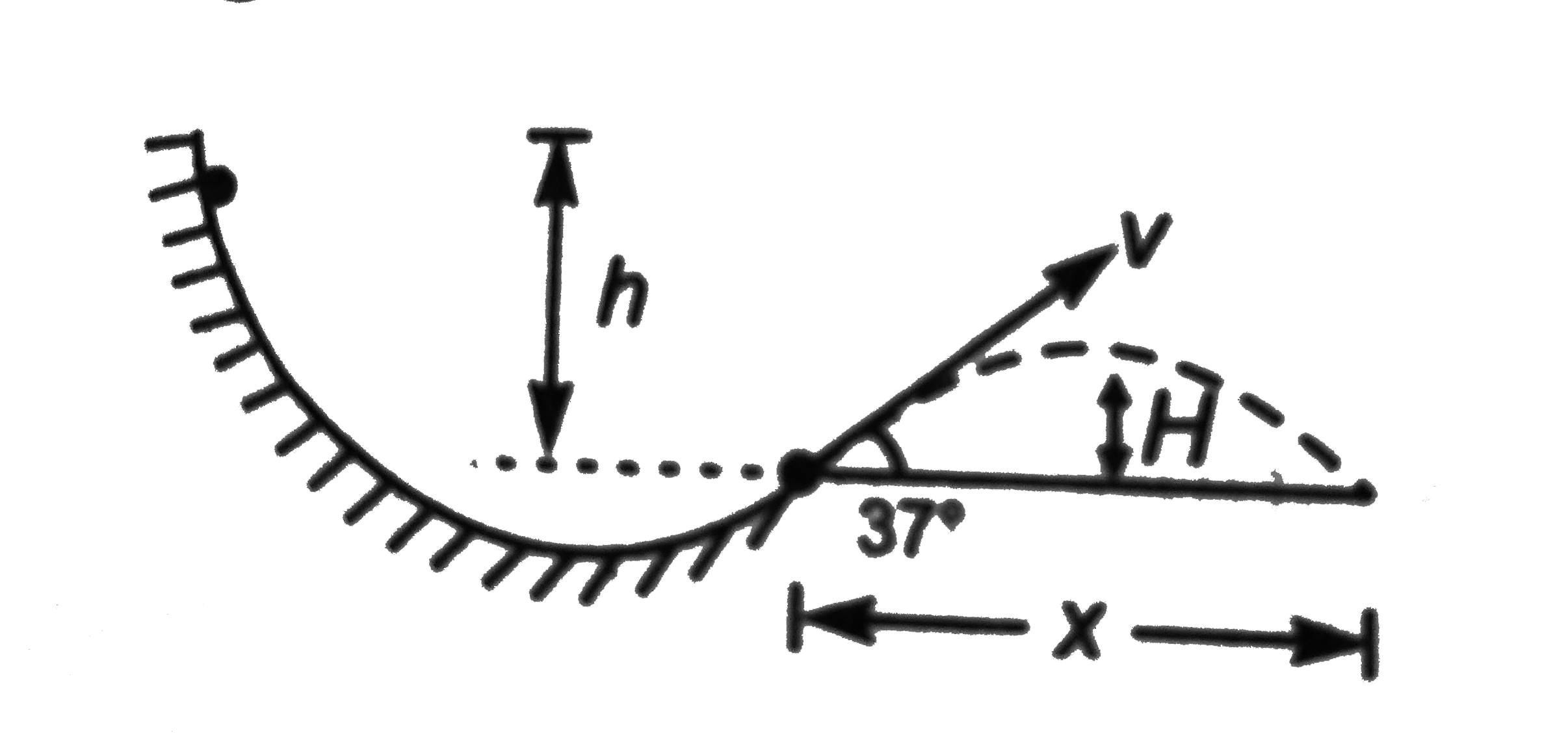
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of `37^(@)` with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Maximum height reached by ball `H` above ground is
View Solution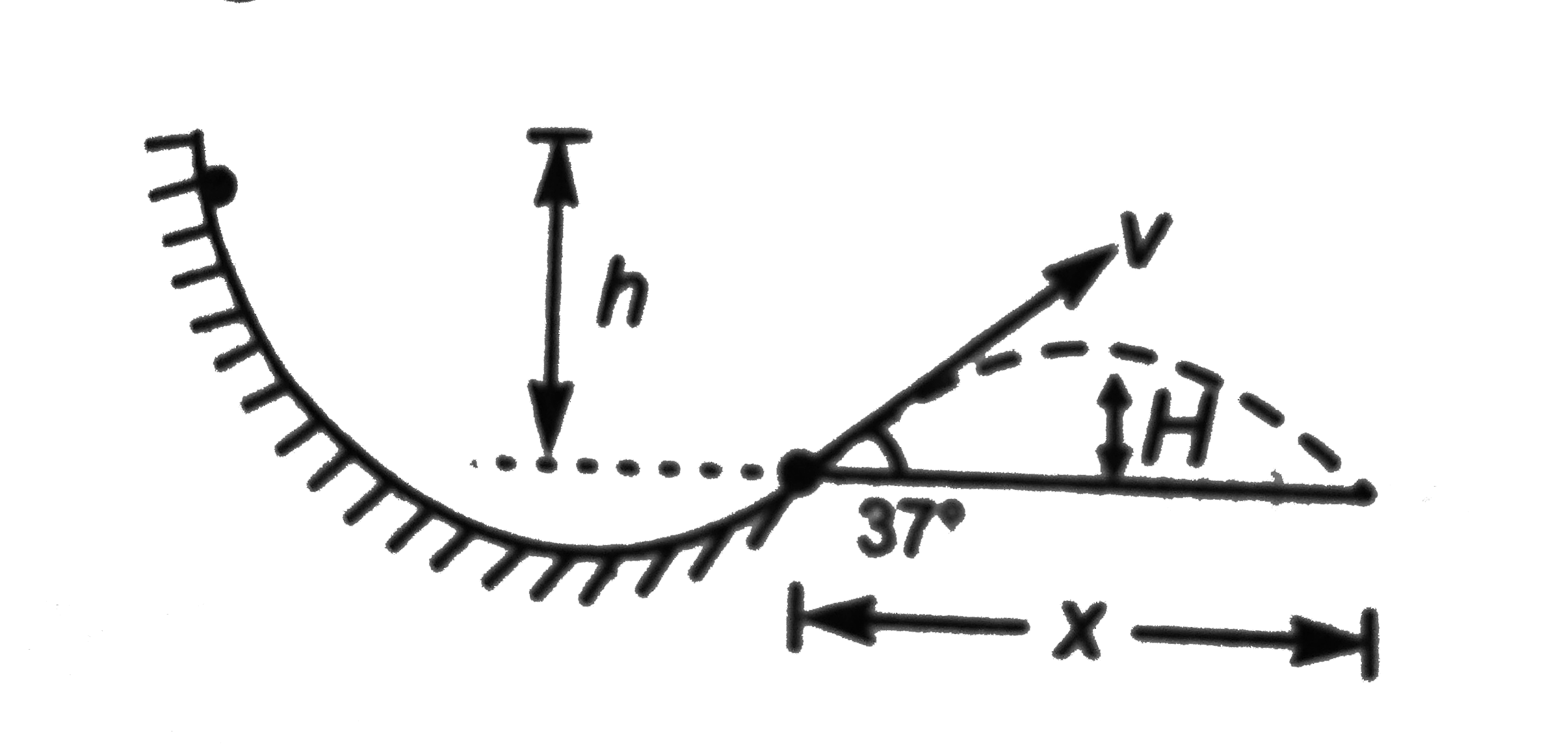
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of `37^(@)` with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Range `x` of the ball is
View Solution
Level 2 Multiple Correct questions and complete solutions for chapter ROTATIONAL MECHANICS of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS ROTATIONAL MECHANICS
- Assertion And Reason
- Examples
- Exercise 12.1
- Exercise 12.10
- Exercise 12.11
- Exercise 12.2
- Exercise 12.3
- Exercise 12.4
- Exercise 12.5
- Exercise 12.6
- Exercise 12.7
- Exercise 12.8
- Exercise 12.9
- Level 1 Objective
- Level 1 Subjective
- Level 2
- Level 2 Multiple Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Example
- Solved Examples
- Subjective Questions