Complete Solutions to Level 2 Subjective of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| DC PANDEY | Level 2 Subjective |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |

Figure shows three identical yo-yos initially at rest on a horizontal surface. For each yo-yo the string is pulled In the direction shown. In each case there is sufficient friction for the yo-yo to roll without slipping. Draw the free-body diagram for each yo-yo in what direction will each yo-yo rotate?
View Solution
A uniform rod of mass `m` and length `l` is held horizontally by two vertical strings of negligible mass, as shown in the figure.
(a). Immediately after the right string is cut, what is the linear acceleration of the end of the rod?
(b). Of the middle of the rod?
(c). Determine the tension in the left string immediately after the right string is cut.
View SolutionA solid disk is rolling without slipping on a level surface at a constant speed of `2.00m//s`. How far can it roll up a `30^(@)` ramp before it stops? (take `g=9.8m//s^(2))`
View SolutionA lawn roller in the form of a thin-walled hollow cylinder of mass `M` is pulled horizotally with a constant horizontally force `F` applied by a handle attached to the axle. If it rolls without slipping. Find the acceleration and the friction forces.
View Solution
Due to slipping points A and B on the rim of the disk have the velocities shown. Determine the velocities of the centre point C and point F at this instant.
View Solution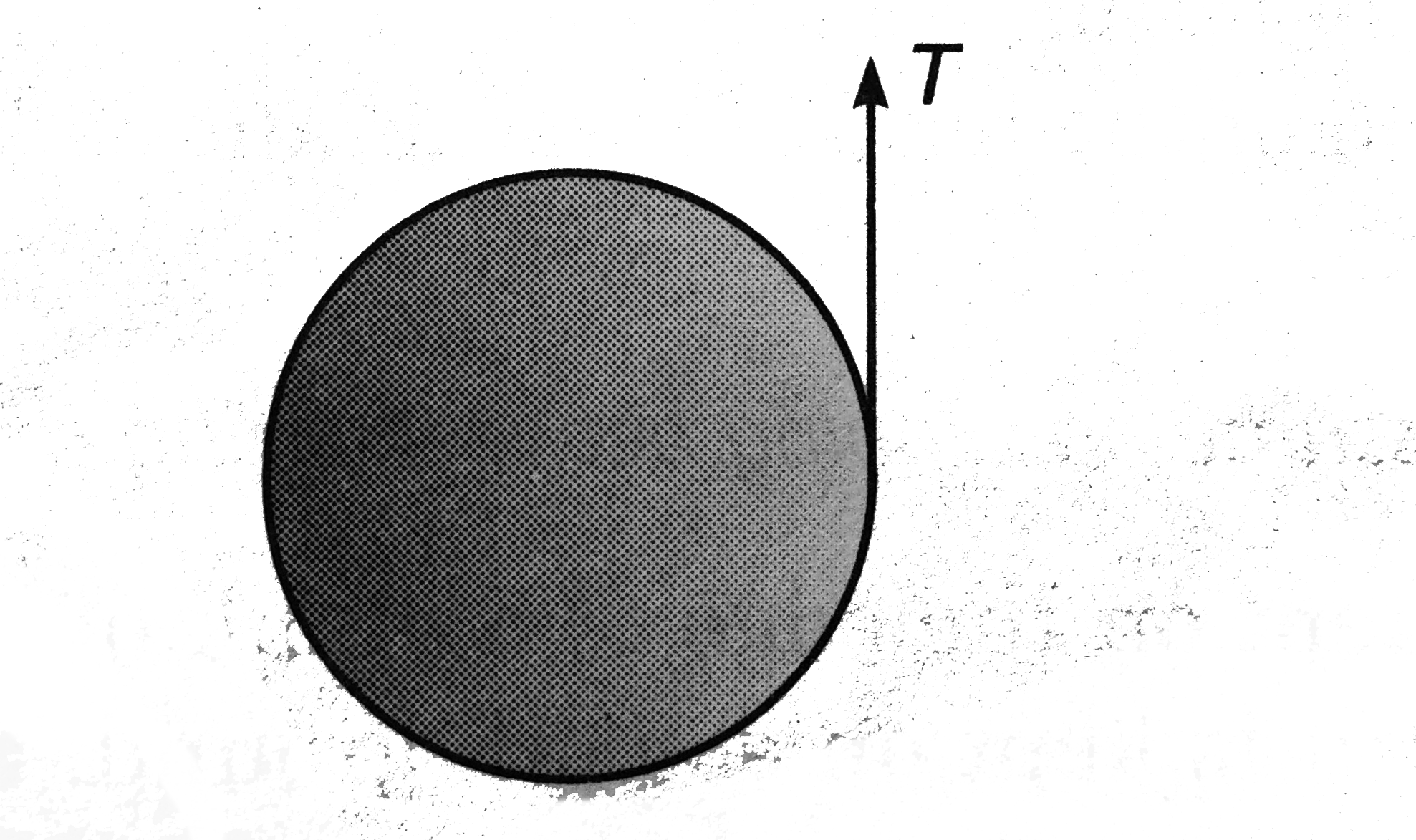
A uniform cylider of mass `M` and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure.
(a). Show that the acceleration of the cylinder is downward with magnitude `a=(2g)/(3)`
(b). Find the tension in the string.
View Solution
A uniform disc of mass `M` and radius R is pivoted about the horizontal axis through its centre `C` A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when `m` reaches the bottom point B.
View SolutionA disc of radius `R` and mass `m` is projected on to a horizontal floor with a backward spin such that its centre of mass speed is `v_(0)` and angular velocity is `omega_(0)`. What must be the minimum value of `omega_(0)` so that the disc eventually returns back?
View Solution
A ball of mass `m` and radius `r` rolls along a circular path of radius `R` its speed at the bottom `(theta=0^(@))` of the path is `v_(0)` find the force of the path on the ball as a function of `theta`.
View Solution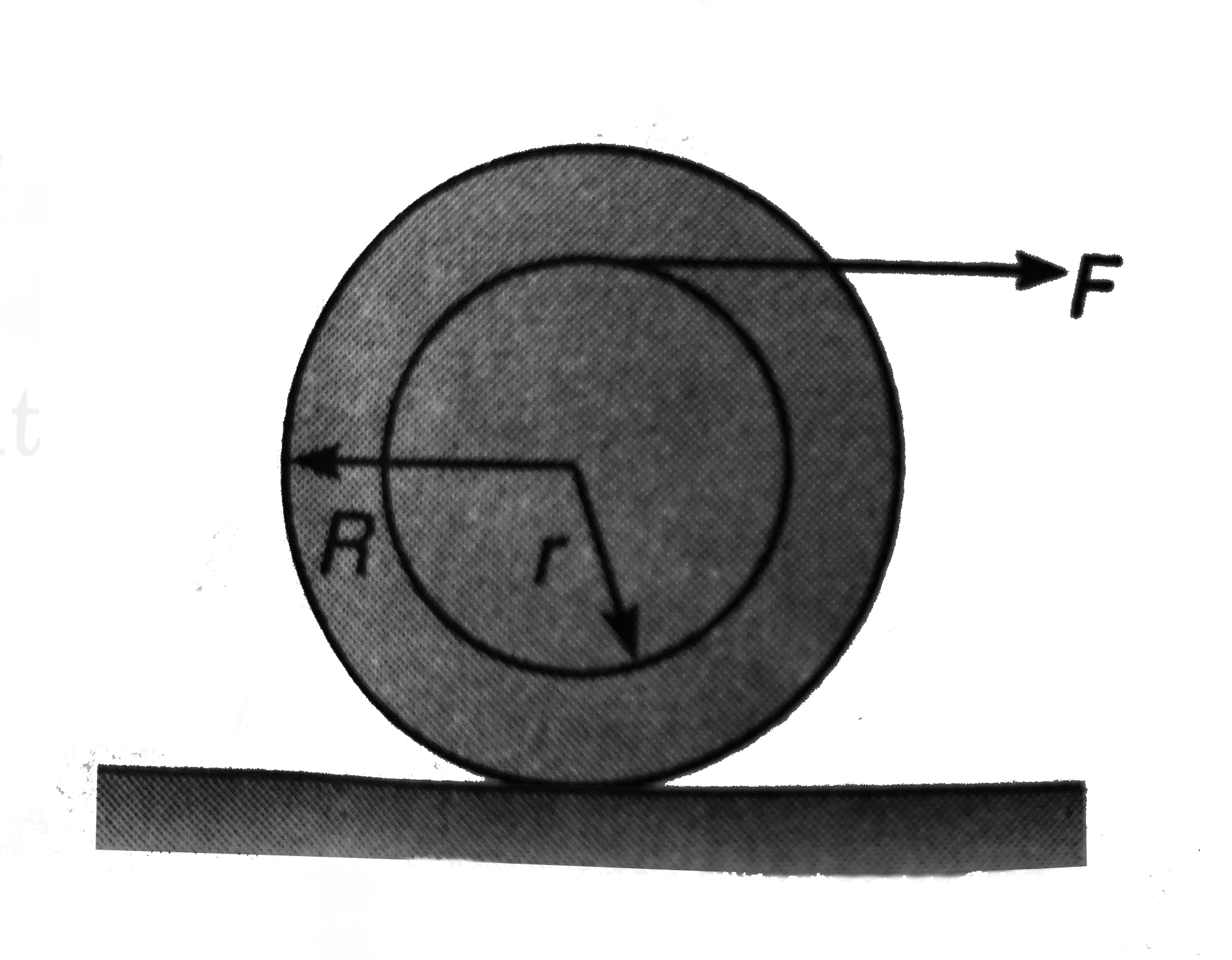
A heavy homogeneous cyliner has mass `m` and radius `R`. It is accelerated by a force `F` which is applied through a rope wound around a light drum of radius r attached to the cylinder (figure) the coefficient of static friction is sufficient for the cylinder to roll without slipping.
View SolutionA man pushes a cylinder of mass `m_1` with the help of a plank of mass `m_2` as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and
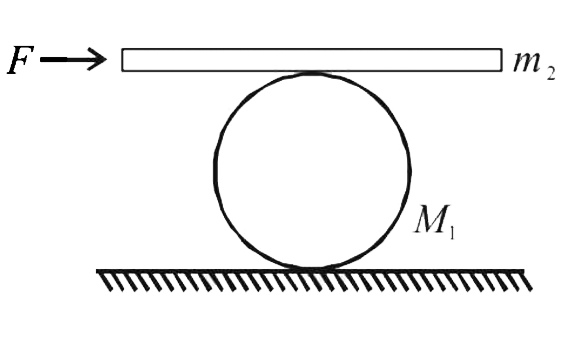
(b) the magnitudes and direction of frictional force at contact points.
View Solution
For the system shown in figure, `M=1kg` `m=0.2` kg, `r=0.2m` calculate `(g=10m//s^(2))`
(a). The linear acceleration of hoop,
(b). The angular acceleration of the hoop of mass `M` and
(c). The tension in the rope.
View SolutionA cylinder of mass `m` is kept on the edge of a plank of mass `2m` and length `12 m`, which in turn is kept on smooth ground. Coefficient of friction between the plank and the cylinder is `0.1`. The cylinder is given an impulse, which imparts it a velocity `7 ms^(-1)` but no angular velocity. Find the time after which the cylinder falls off the plank.
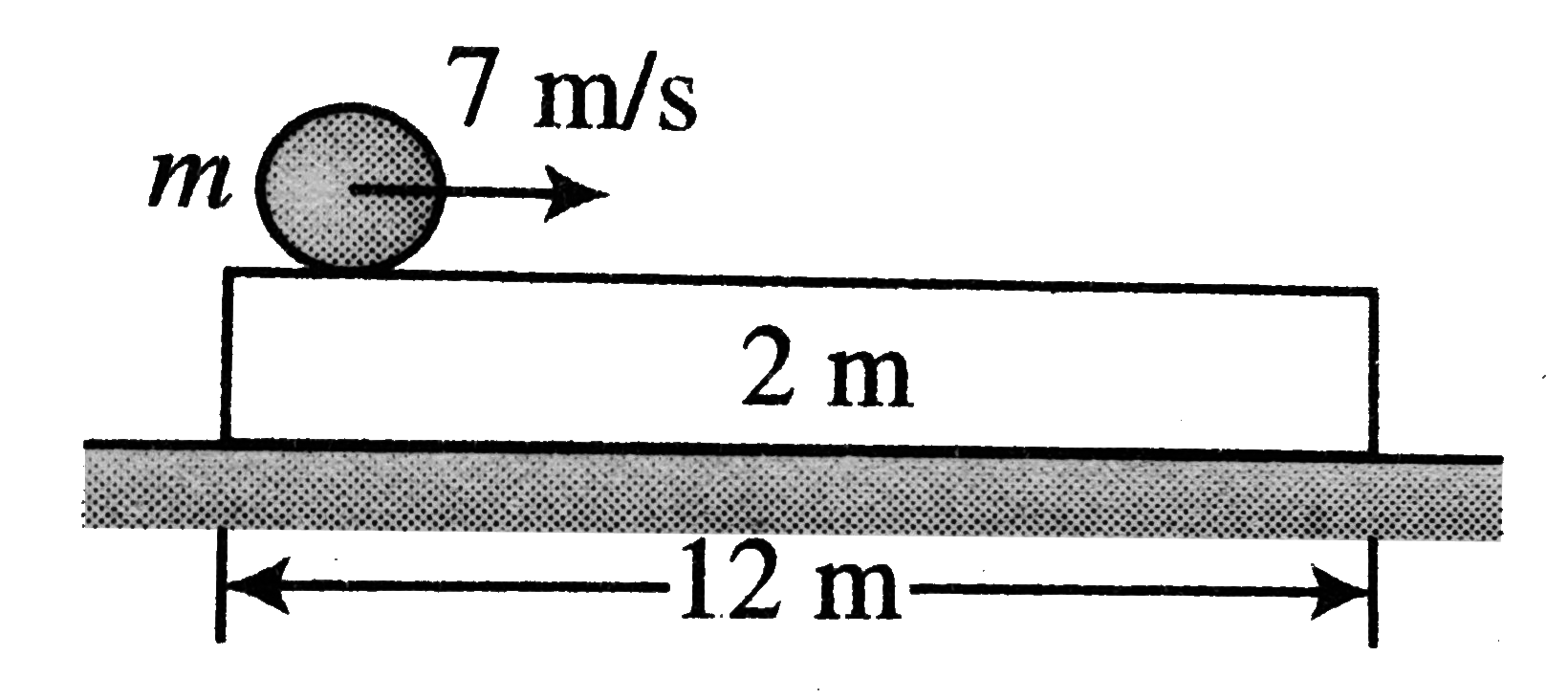
View Solution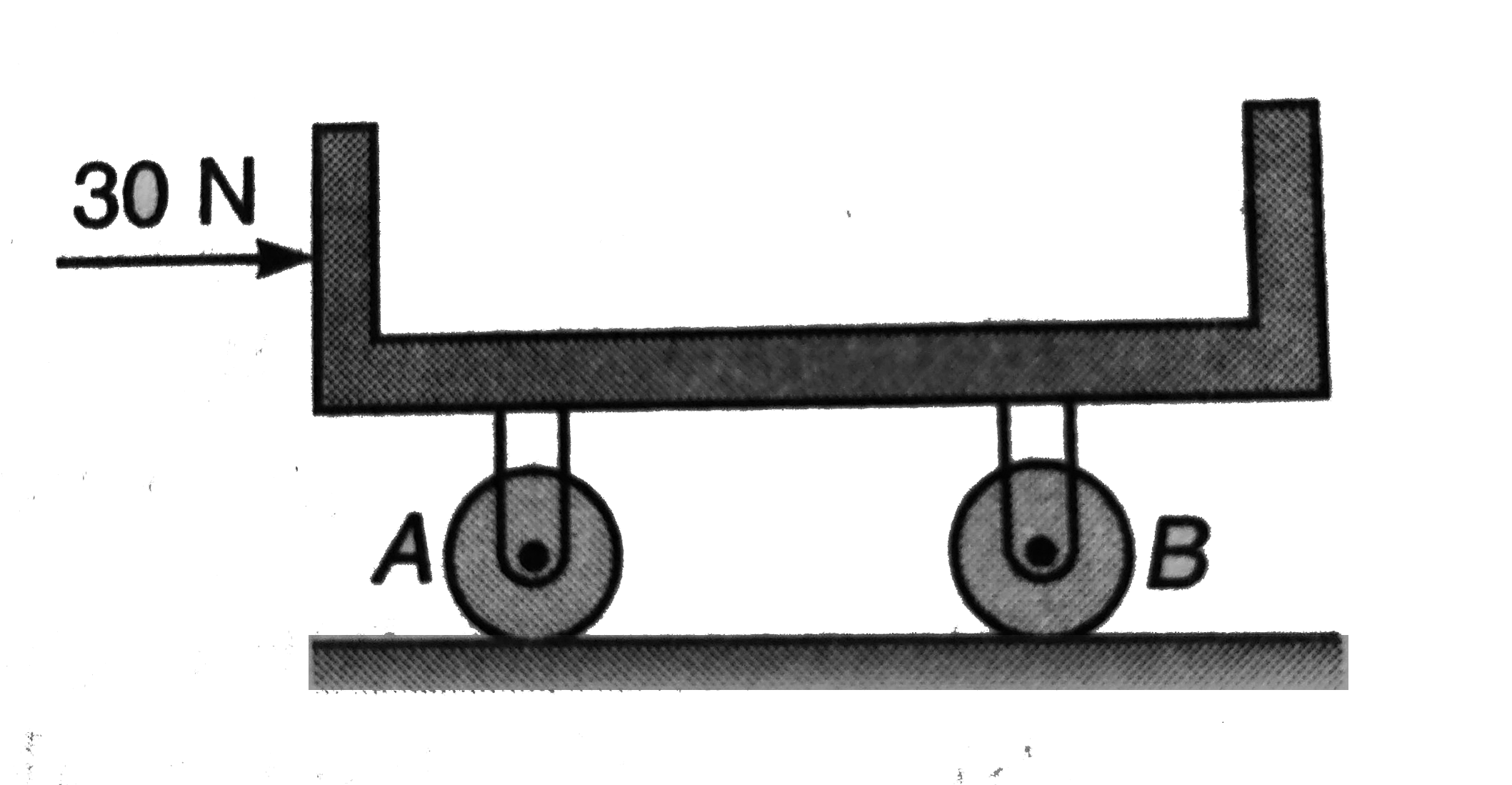
The 9 kg cradle is supported as shown by two uniform disks that roll without sliding at all surfaces of contact. The mass of each disk is `m=6kg` and the radius of each disk is `r=80mm`. Knowing that the system is initially at rest, determine the velocity of the cradle after it has moves 250 mm.
View Solution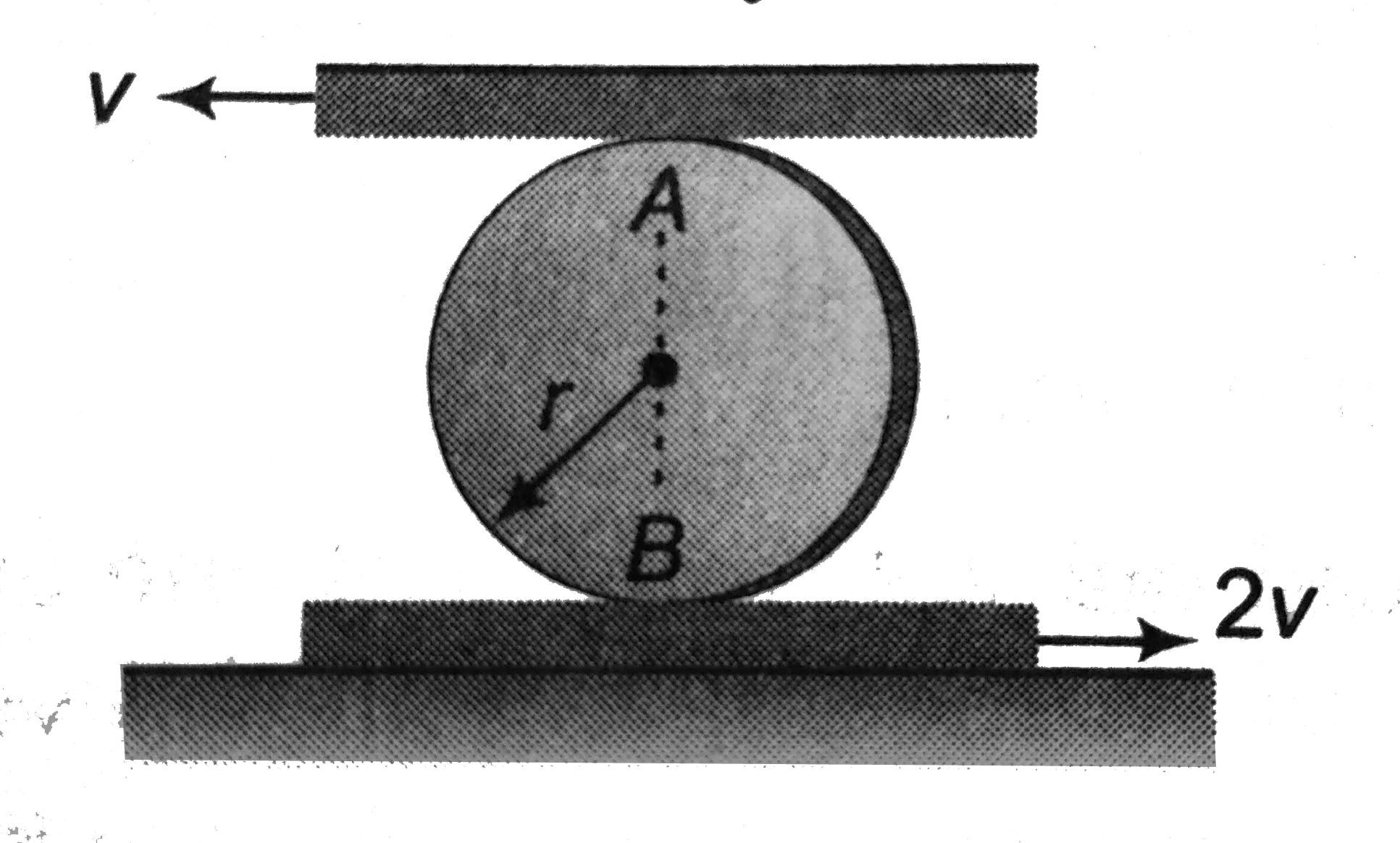
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View Solution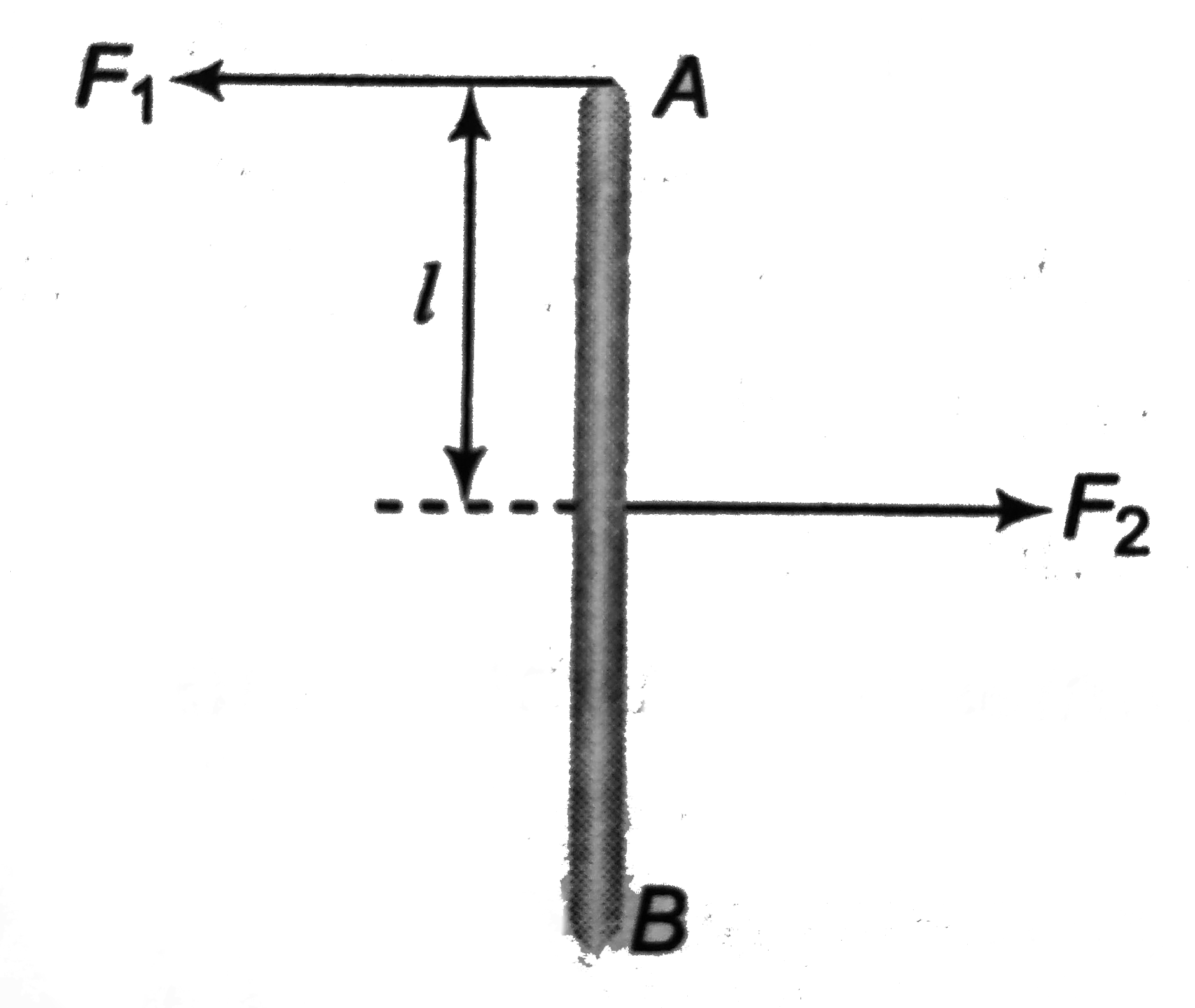
A thin uniform rod AB of mass `m=1kg` moves translationally with acceleration `a=2m//s^(2)` and to two anitiparallel forces `F_(1)` and `F_(2)`. The distance between the points at which these forces are applied is equal to `l=20cm` besides it is known that `F_(2)=5N` find the length of the rod.
View Solution
The assembly of two discs as shown in figure is placed on a rough horizontal surface and the front disc is given an initial angular velocity `omega_(0)`. Determine the final linear and angular velocity when both the discs start rolling. it is given that friction is sufficient to sustain rolling the rear wheel from the starting of motion.
View Solution
A horizontal plank having mass `m` lies on a smooth horizontal surface. A sphere of same mass and radius `r` is spined to angular frequency `omega_(0)` and gently placed on the plank as shown in the figure. If coefficient of friction between the plank and the sphere is `mu`. Find the distance moved by the plank till sphere starts pure rolling on the plank. the plank is long enough.
View SolutionA ball rolls without sliding over a rough horizontal floor with velocity `v_(0)=7m//s` towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is `e=0.7`. Calculate velocity `v` of the ball after the collision.
View SolutionA sphere a disk and a hoop made of homogeneous materials have the same radius (10 cm) and mass (3kg) They are released from rest at the top of a `30^(@)` incline and roll down without slipping through a vertical distance of 2m. `(g=9.8m//s^(2))`
(a). What are their speeds at the bottom?
(b). findt the friction force `f` each case
(c). if they start together at `t=0`, at what time does each reach the bottom?
View SolutionABC is a triangular framwork of three uniform rods each of mass `m` and length `2l`. It is free to rotate in its own plane about a smooth horizontal axis through A which is perpendicular to ABC. If it is released from rest when AB is horizontal and C is above AB. Find the maximum velocity of C in the subsequent motion.
View SolutionA uniform stick of length `L` and mass `M` hinged at end is released from rest at an angle `theta_(0)` with the vertical show that when the angle with the vertical is `theta`. The hinge exerts of force `F_(r)` along the stick and `F_(t)` perpendicular tot he stick given by `F_(r)=(1)/(2)Mg(5costheta-3costheta_(0))` and `F_(t)=(1)/(4)Mgsintheta`
View SolutionA uniform rod AB of mass 3m and length 4l, which is free to turn in a vertical plane about a smooth horizontal axis through A, is released from rest when horizontal. When the rod first becomes vertical, a point C of the rod, where AC=3l strikes a fixed peg. Find the linear impulse exerted by the peg on the rod if
(a). The rod is brought to rest by the peg.
(b). The rod rebounds and next comes to instantaneous rest inclined to the downward vertical at an angle `(pi)/(3)` radian.
View Solution
A uniform rod of length 4l and mass `m` is free to rotate about a horizontal axis passing through a point distant `l` from its one end. When the rod is horizontal its angular velocity is `omega` as shown in figure. calculate
(a). reaction of axis at this instant,
(b). Acceleration of centre of mass of the rod at this instant.
(c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time.
(d). minimum value of `omega`, so that centre of rod can complete circular motion.
View Solution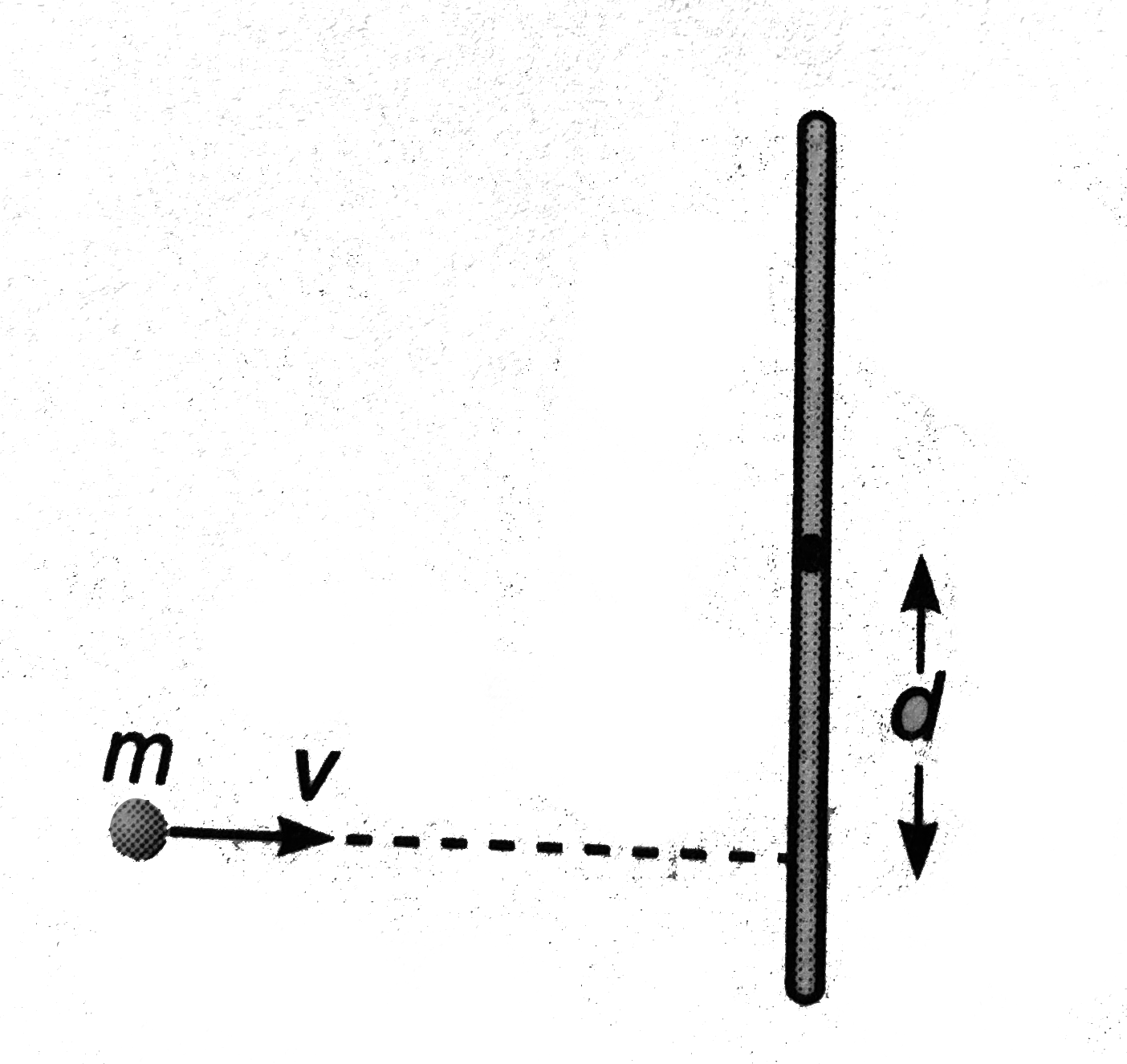
A stick of length `l` lies on horizontal table. It has a mass `M` and is free to move in any way on the table. A bal of mass `m` moving perpendicularly to the stick at a distance d from its centre with speed `v` collides elastically with it as shown in figure. what quantities are conserved in the collision ? what must be the mass of the ball, so that it remains at rest immediately after collision?
View Solution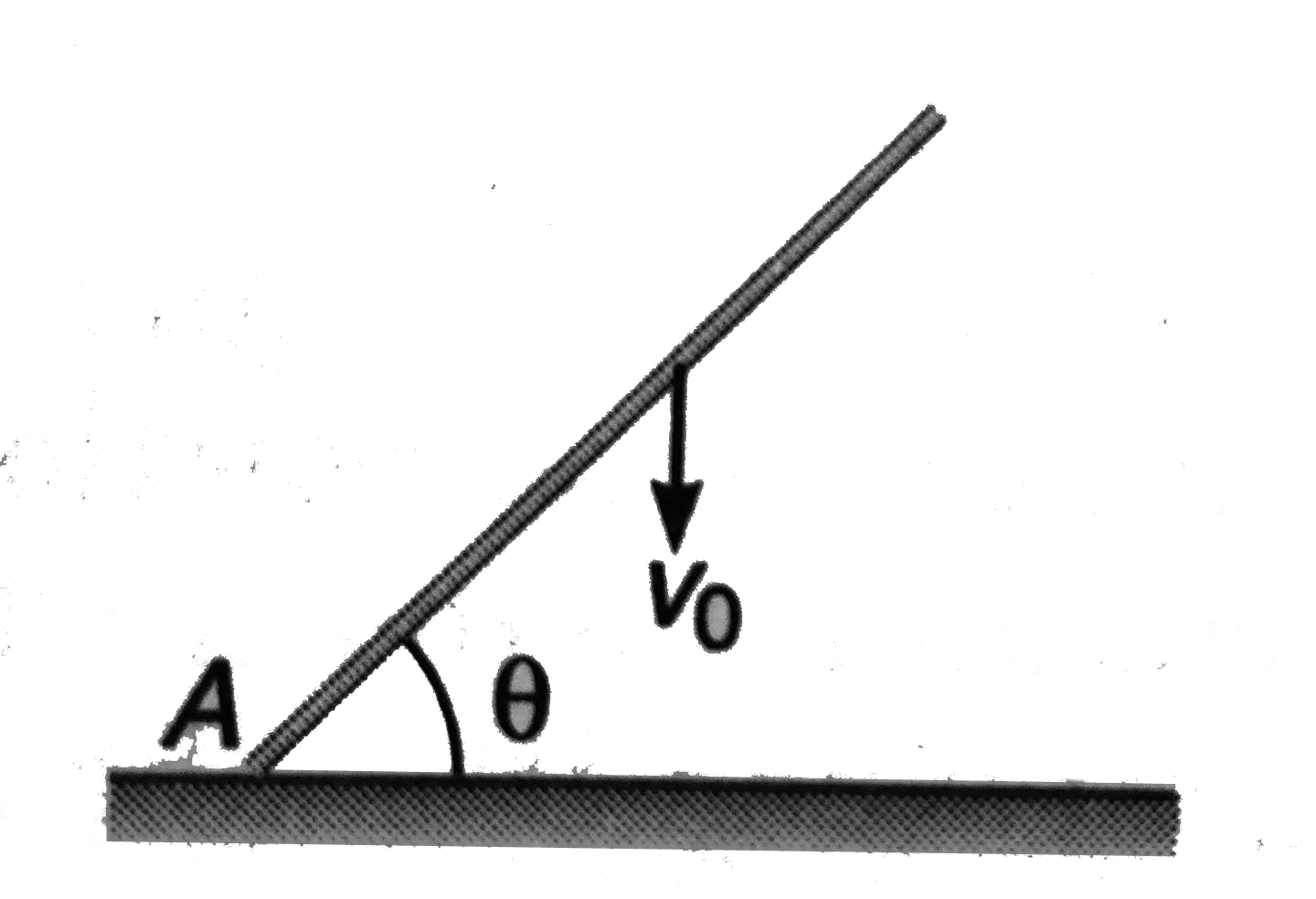
A rod of length `l` forming an angle `theta` with the horizontal strikes a frictionless floor at A with its centre of mass velocity `v_(0)` and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.
View SolutionThree particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizontal frictionless table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity `omega`.
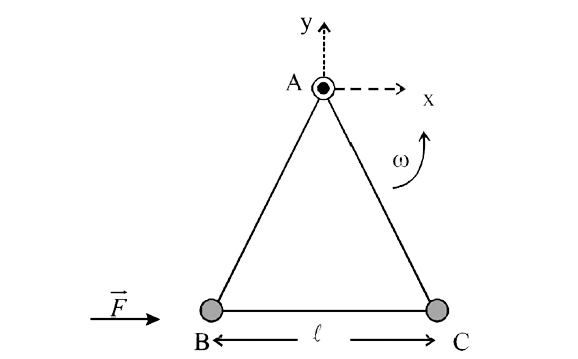
(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
View Solution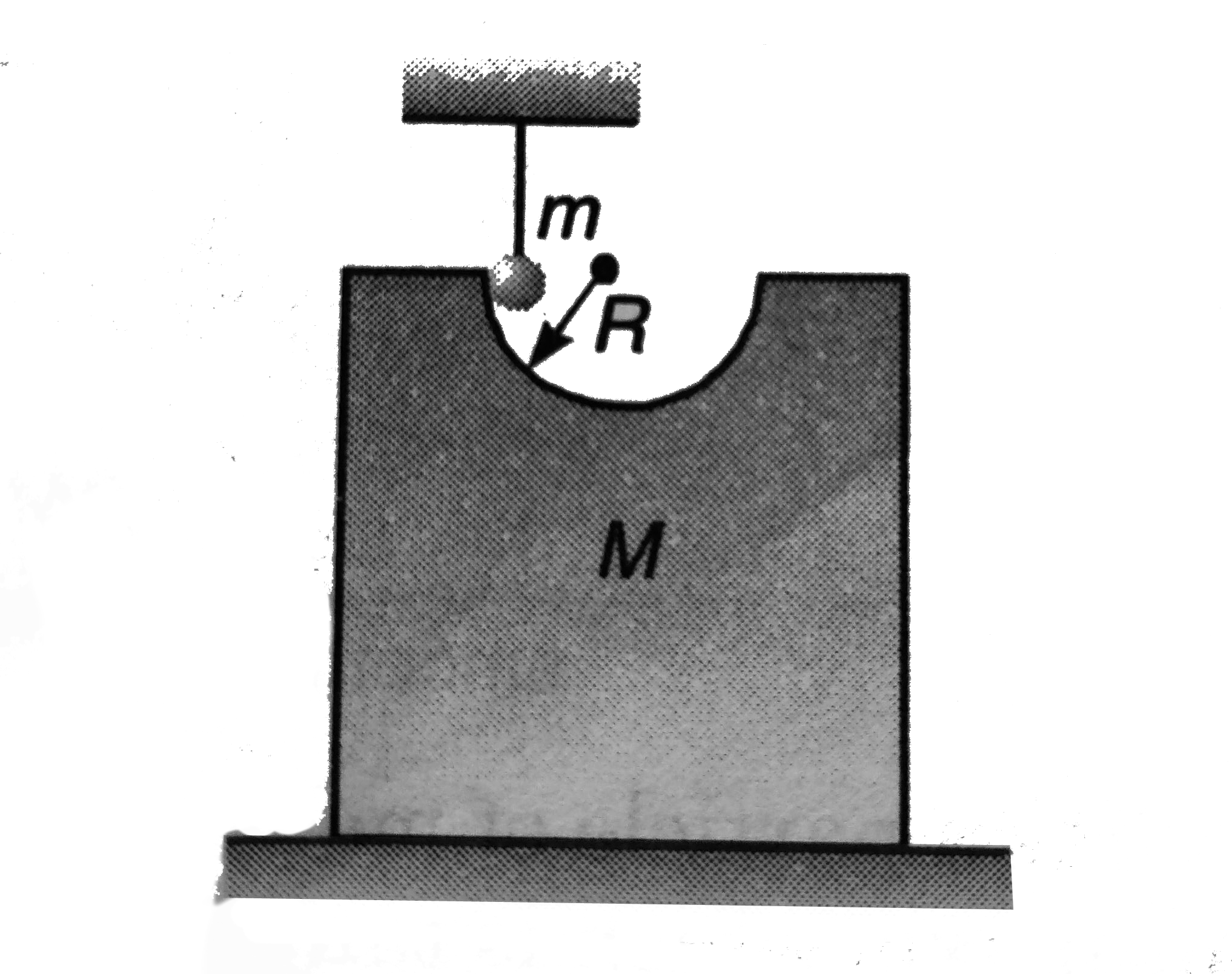
A semicircular track of radius `R=62.5cm` is cut in a block. Mass of block having track, is `M=1kg` and rests over a smooth horizontal floor. A cylinder of radius `r=10`cm and mass `m=0.5kg` is hanging by thread such that axes of cylinder and track are in same level and surface of cylinder is in contact with the track as shown in figure When the thread is burnt, cylinder starts to move down the track. Sufficient friction exists between surface of cylinder and track, so that cylinder does not slip.
Calculate velocity of the block when it reaches bottom of the track. Also find force applied by block on the floor at that moment. `(g=10m//s^(2))`
View SolutionA uniform circular cylinder of mass `m` and radius `r` is given an initial angular velocity `omega_()` and no initial translational velocity it is placed in contact with a plane inclined at an angle `alpha` to the horizontal. If there is a coefficient of friction `mu` for sliding between the cylinder and plane. Find the distance the cylinder moves up before sliding stops also calculate the maximum distance it travels up the plane assume `mugttanalpha`.
View SolutionShow that if a rod held at angle `theta` to the horizontal and released, its lower end will not slip if the friction coefficient between rod and ground is greater than `(3sinthetacostheta)/(1+3sin^(2)theta)`
View Solution
One-fourth length of a uniform rod of mass `m` and length `l` is placed on a rough horizontal surface and it is held stationary in horizontal position by means of a light thread as shown in the figure. The thread is then burnt and the rod start rotating about the edge. Find the angle between the rod and the horizontal when it is about to slide on the edge. The coefficient of friction between the rod and surface is `mu`.
View Solution
in figure the cylinder of mass `10kg` and radius 10 cm has a tape wrapped round it. The pully weighs 100 N and has a radius 5 cm. When the system is released the 5 kg mass comes down and the cylinder rolls without slipping. Calculate the acceleration and velocity of the mass as a function of time.
View Solution
A cylinder is sandwiched between two planks. Two constant horizontal forces `F` and `2F` are applied on the planks as shown. Determine the acceleration of the centre of mass of cylinder and the top plank. If there is no slipping at the top and bottom of cylinder.
View Solution
A ring of mass `m` and radius `r` has a particle of mass `m` attached to it at a point A. the ring can rotate about a smooth horizontal axis which is tangential to the ring at a point B diametrically opposite to A. The ring is released from rest when AB is horizontal. find the angular velocity and the angular acceleration of the body when AB has turned through an angle `(pi)/(3)`.
View Solution
a hoop is placed on the rough surface such that it has an angular velocity `omega=4rad//s` and an angular deceleration `alpha=5rad//s^(2)` also its centre has a velocity of `v_(0)=5m//s` and a deceleration `a_(0)=2m//s^(2)` determine the magnitude of acceleration of point B at this instant.
View Solution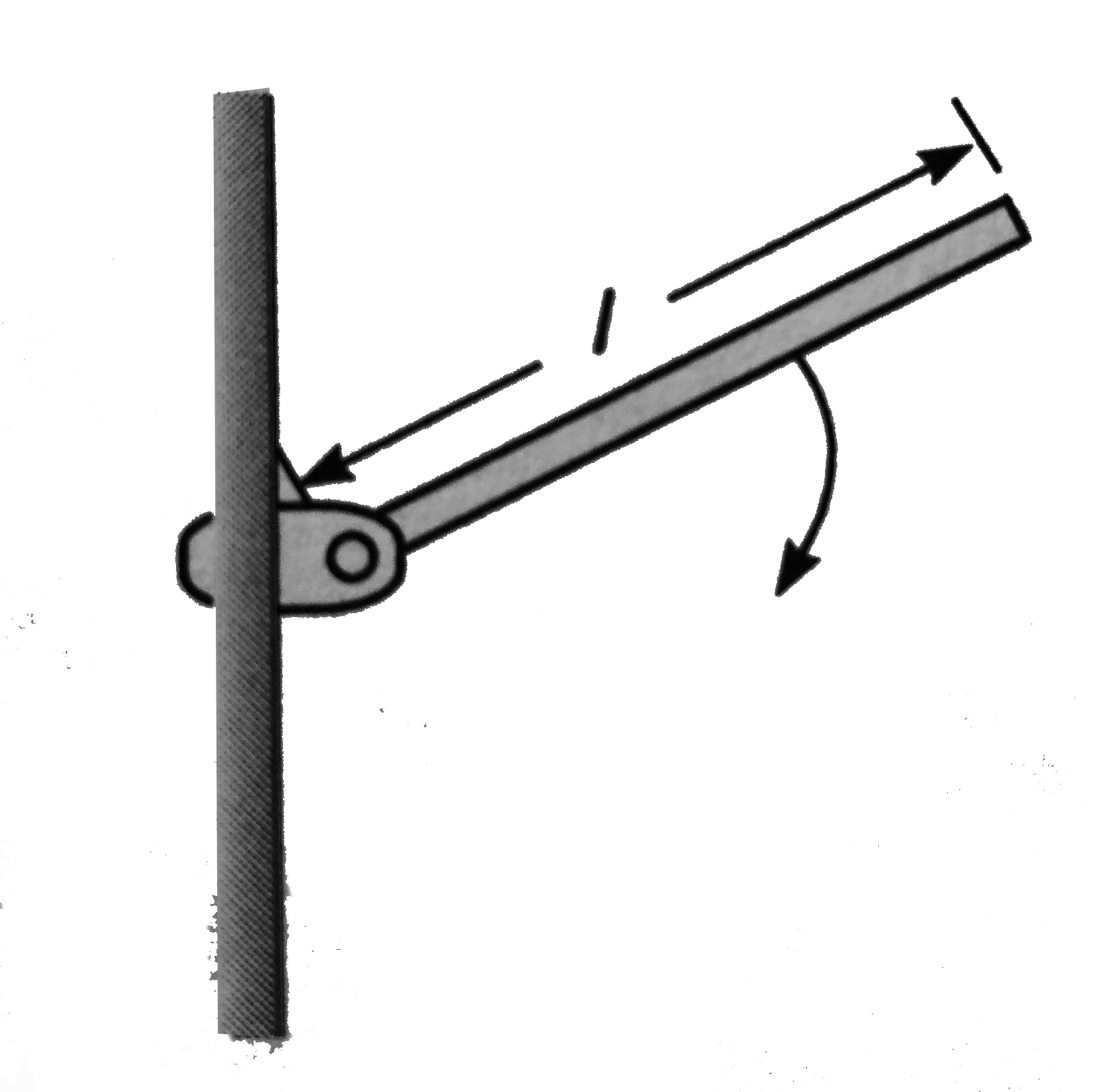
A thin plank of mass `M` and length `l` is pivoted at one end. The plank is releaed at `60^(@)` from the vertical. What is the magnitude and direction of the force on the pivot when the plank is horizontal?
View Solution
Level 2 Subjective questions and complete solutions for chapter ROTATIONAL MECHANICS of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS ROTATIONAL MECHANICS
- Assertion And Reason
- Examples
- Exercise 12.1
- Exercise 12.10
- Exercise 12.11
- Exercise 12.2
- Exercise 12.3
- Exercise 12.4
- Exercise 12.5
- Exercise 12.6
- Exercise 12.7
- Exercise 12.8
- Exercise 12.9
- Level 1 Objective
- Level 1 Subjective
- Level 2
- Level 2 Multiple Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Example
- Solved Examples
- Subjective Questions