Complete Solutions to INTEGER_TYPE of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| DC PANDEY MASTER PROBLEM PACKAGE | INTEGER_TYPE |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
A particle is projected with velocity `2(sqrt(gh))`, so that it just clears two walls of equal height h which are at a distance of 2h form each other. Show that the time of passing between the walls is `2 (sqrt (h/g)).` [Hint : First find velocity at height h. Treat it as initial velocity and 2h as the range. ]
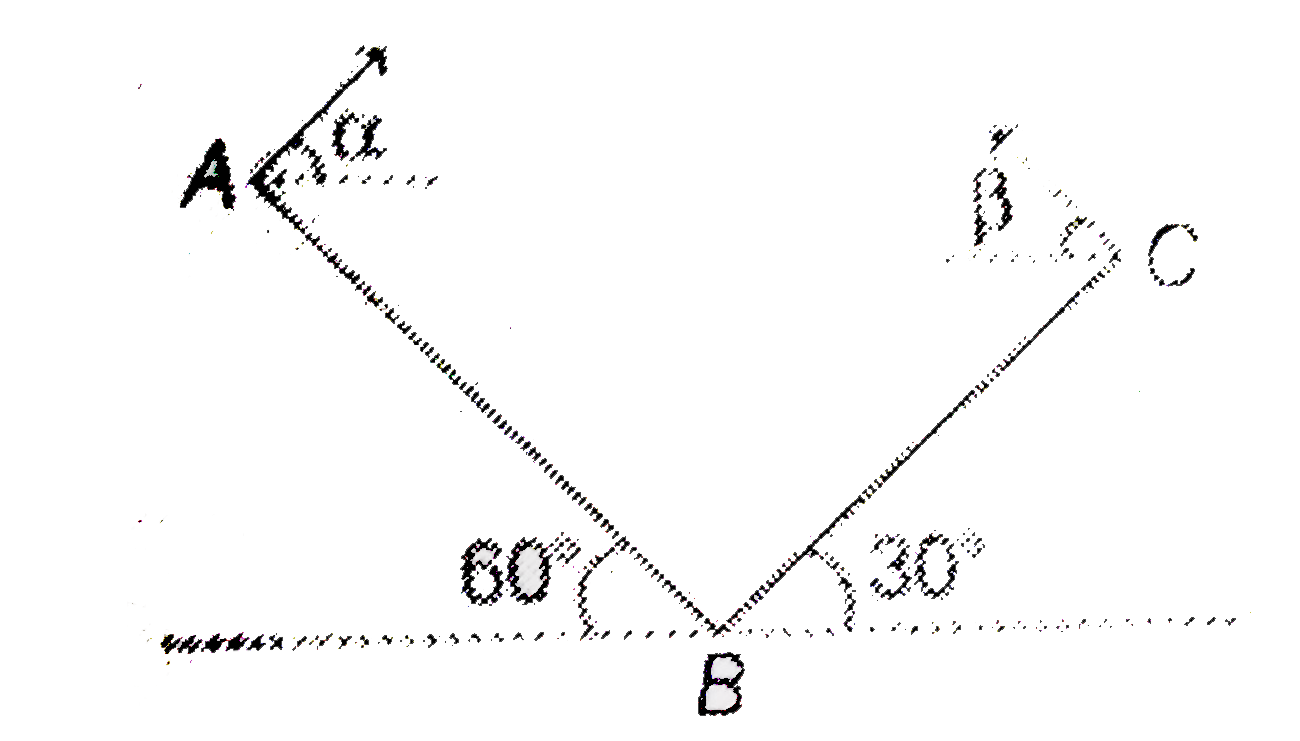
View SolutionTwo inclined planes `AB` and `BC` are at inclinations of `60^(@)` and `30^(@)` as shown in the figure. The two projectiles are thrown simultaneously from `A` and `C` with speed `2m//s` and `v_(0)` respectively. They strike at `B` with same speed. If length of `AB` is `1/(sqrt(3))m`and `BC` is `1m,` then find the value of `v_(0)` ( in m/s)
View SolutionA particle moves along a parabolic path `y=-9x^(2)` in such a way that the `x` component of velocity remains constant and has a value `1/3m//s`. Find the instantaneous acceleration of the projectile (in `m//s^(2)`)
View SolutionA ground to ground projectile is at point A at `t = (T)/(3)`, is at point B at `t = (5T)/(6)` and reaches the ground at `t = T`. The difference in heights between points A and B is
View SolutionAn object is projected with a velocitiy of `20m//s` making an angle of `45^(@)` with horizontal. The equation for trajectory is `h=Ax-Bx^(2)` where `h` is height `x` is horizontal distance. `A` and `B` are constants. The ratio `A.B` is `x/0.1`. Find value of `x.(g=10m//s^(2))`
View SolutionA ball is thrown from the ground to clear a wall `3m` high at a distance of `6m` and falls `18m` away from the wall, the angle of projection of ball is `tan^(-1)(2/x)`. Find value of `x`.
View SolutionA particle is thrown from the origin,at an angle `theta(0lttheta lt 90^(@))` such that it just crosses a wall of height `9m`. Wall is at `x=12m`. Speed of projection is `nsqrt(3)m/s` and particle strikes the ground at `x=48m`. Value of `n` is `(g=10m//s^(2))`
View Solution`ABC` is a triangle in vertical plane. Its two base angles `/_BAC` and `/_BCA` are `45^(@)` and `"tan"^(-1)1/3` respectively. A particle is projected from point `A` such that is passes through vertices `B` and `C`. Angle of projectio is `theta`. Find the value of `3 tan theta`.

View SolutionA stone is projected from point `P` on the inclined plane with velocity `v_(0) = 10 m//sec` directed perpendicular to the plane. The time taken (in second) by the stone to strike the horizontal ground `S` is (Given `PO = l = 10`meter)(Take `g = 10m//s^(2)`)

View SolutionA stone is thrown from the top of a tower of height `h=10m` with speed `v-10m//s`. The distance of the landing point on the ground from the foot of the tower is `Rle2sqrt(3)k` in meter. Calculate `k`. Take `g=10m//s^(2)`
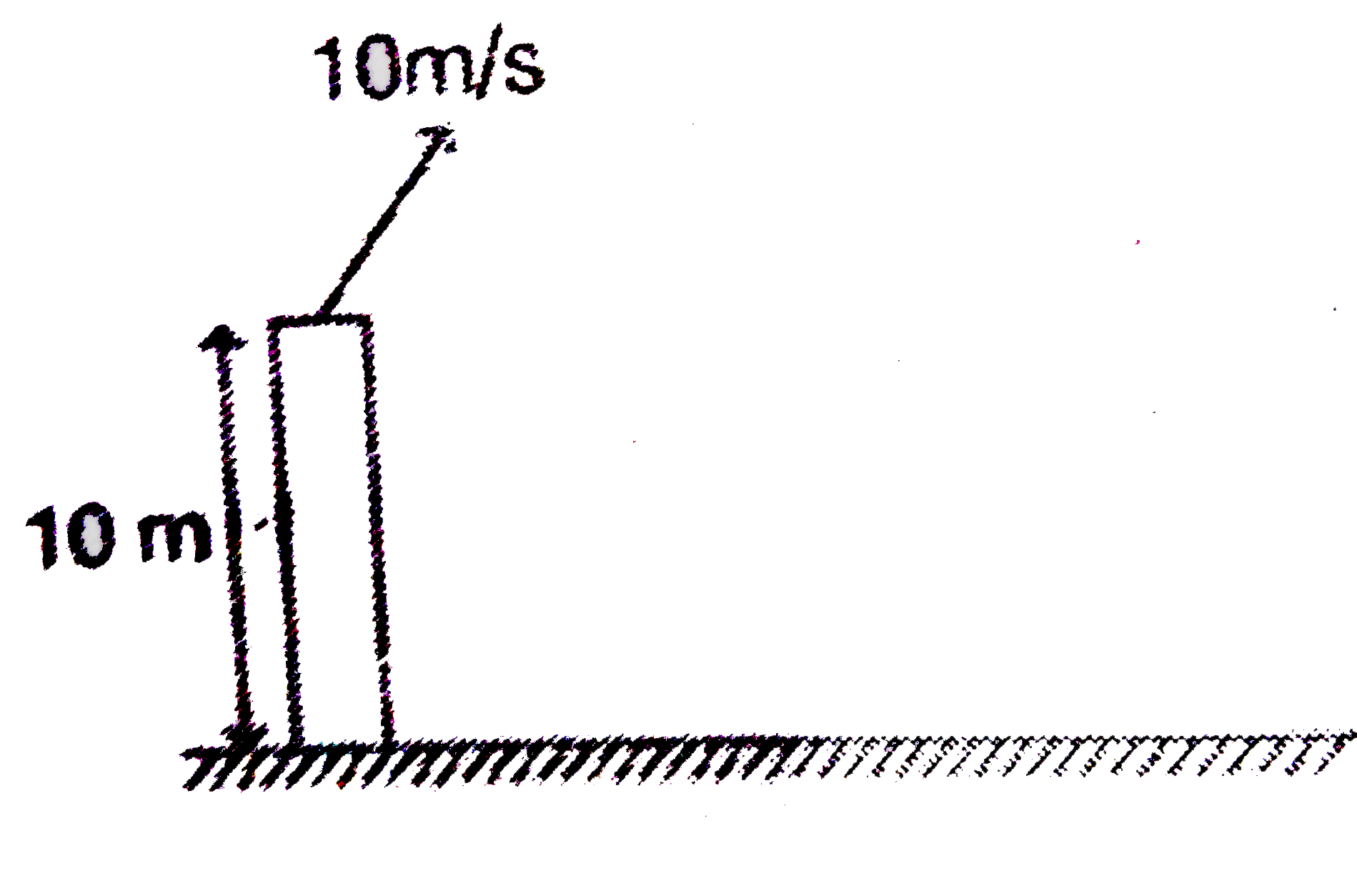
View Solution
INTEGER_TYPE questions and complete solutions for chapter KINEMATICS of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY MASTER PROBLEM PACKAGE Class 11 PHYSICS KINEMATICS
- Assertion And Reason
- Comprehension
- COMPREHENSION_TYPE
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Exercise 6.1
- Exercise 6.2
- Exercise 6.3
- Exercise 6.4
- Exercise 6.5
- Exercise 6.6
- Exercise 6.7
- Exercise 6.8
- Exercise 6.9
- INTEGER_TYPE
- MATCH THE COLUMN
- MCQ_TYPE
- Miscellaneous Example
- More Than One Correct
- Objective
- SCQ_TYPE
- Subjective
- Subjective Questions