Complete Solutions to Subjective of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| DC PANDEY | Subjective |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
Velocity of particle moving along positive x-direction is `v = (40-10t)m//s`. Here,t is in seconds. At time `t=0,` tha x coordinate of particle is zero. Find the time when the particle is at a distance of 60 m from origin.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. Plot the corresponding displacement-time graph of the particle if at time `t=0,` displacement `s=0.`
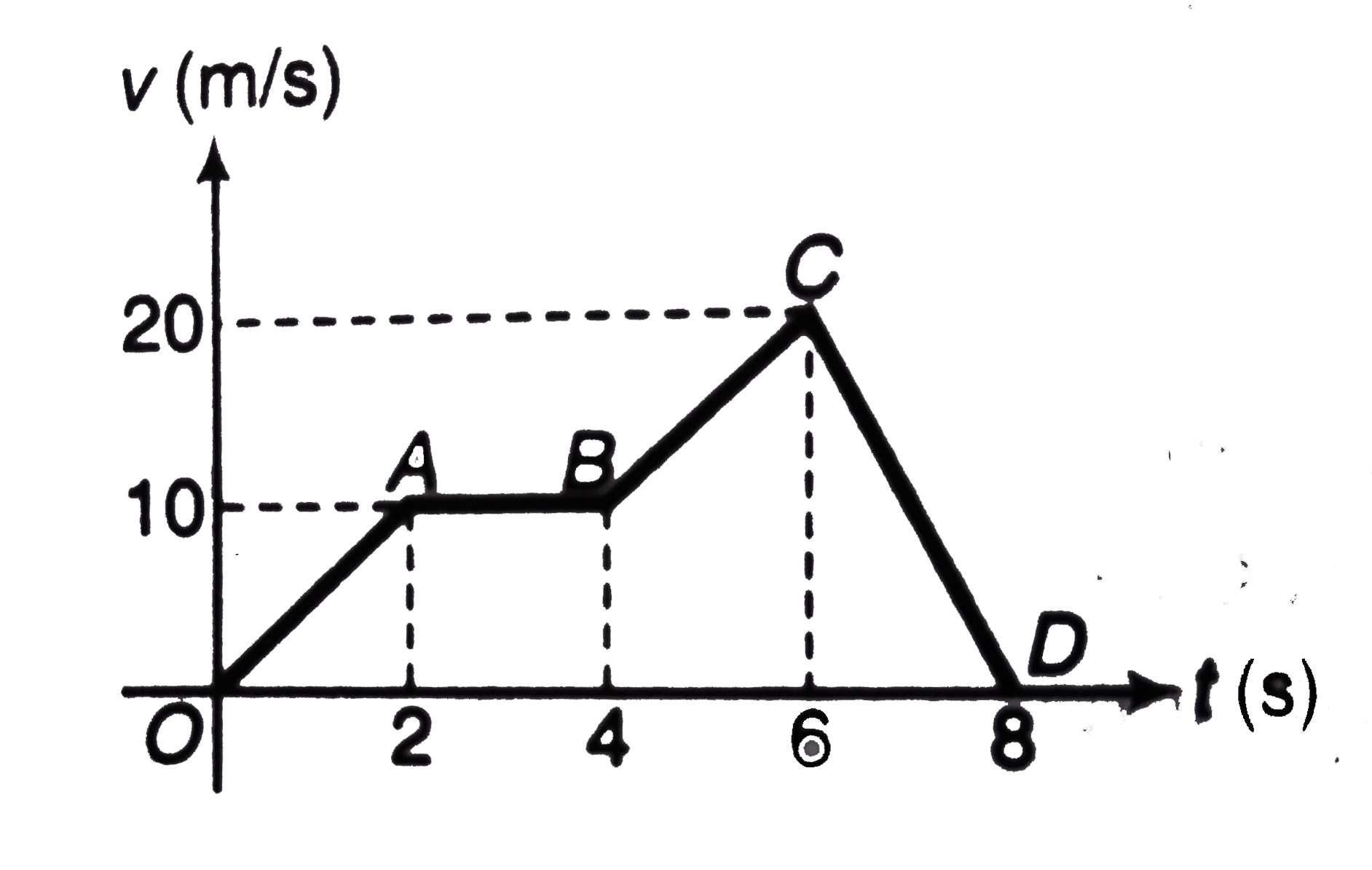
View Solutionvelocity-time graph of a particle moving in a straight line is as shown in figure. At time `t = 0,` velocity of the particle is zero. Find

(a) average acceleration in a time interval from `t = 6 s` to `t = 12 s,`
(b) velocity of the particle at `t = 14 s.`
View SolutionA particle is moving in x-y p1ane.At time t`=0,` particle is at `(1m, 2m)` and has velocity `(4 hat i + 6 hat j) m//s.` At `t = 4s,` particle reaches at `(6m, 4m)` and has velocity `(2 hat i + 10 hat j) m//s.` In the given time interval, find
(a) average velocity,
(b) average acceleration and
(c) from the given data, can you find average speed?
View SolutionA stone is dropped from the top of a tower. When it crosses a point 5 m below the top, another stone is let fall from a point 25 m below the top. Both stones reach the bottom of the tower simultaneously. Find the height of the tower. Take `g = 10 m//s^2.`
View SolutionA point mass starts moving in a straight line with constant acceleration. After time `t_0` the acceleration changes its sign, remaining the same in magnitude. Determine the time T from the beginning of motion in which the point mass returns to the initial position.
View SolutionA football is kicked vertically upward from the ground and a student gazing out of the window sees it moving upwards past her at `5.00 m//s.` The window is `15.0 m` above the ground. Air resistance may be ignored. Take `g=10 m//s^2.`
(a) How high does the football go above ground?
(b) How much time does it take to go from the ground to its highest point?
View SolutionA car moving with constant acceleration covered the distance between two points `60.0 m` apart in `6.00 s.` Its speed as it passes the second point was `15.0 m//s.`
(a) What is the speed at the first point?
(b) What is the acceleration?
(c) At what prior distance from the first was the car at rest?
View SolutionA particle moves along the x-direction with constant acceleration. The displacement, measured from a convenient position, is 2 m at time `t= 0` and is zero when `t= 10 s.` If the velocity of the particle is momentary zero when `t = 6 s,` determine the acceleration a and the velocity v when `t= 10s.`
View SolutionAt time `t= 0,` a particle is at `(2m, 4m).` It starts moving towards positive x-axis with constant acceleration `2 m//s^2` (initial velocity=0). After 2 s, an additional acceleration of `4 m//s^2` starts acting on the particle in negative y-direction also. Find after next 2 s.
(a) velocity and
(b) coordinates of particle.
View SolutionA particle starts from the origin at `t= 0` with a velocity of `8.0 hat j m//s` and moves in the x-y plane with a constant acceleration of `(4.0 hat i + 2.0 hat j) m//s^2.` At the instant the particle's x-coordinate is 29 m, what are
(a) its y-coordinate and
(b) its speed ?
View SolutionThe velocity of a particle moving in a straight line is decreasing at the rate of `3 m//s` per metre of displacement at an instant when the velocity is `10 m//s.` Determine the acceleration of the particle at this instant.
View SolutionA particle moves along a horizontal path, such that its velocity is given by `v = (3t^2 - 6t) m//s,` where t is the time in seconds. If it is initially located at the origin O, determine the distance travelled by the particle in time interval from `t = 0` to `t = 3.5 s` and the particle's average velocity and average speed during the same time interval.
View SolutionA particle travels m a straight line, such that for a short time `2 s le tle 6 s,` its motion is described by `v= (4/a) m//s,` where a is in `m//s^2.` If `v= 6 m//s.` when `t= 2 s,` determine the particle's acceleration when `t= 3 s.`
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its displacement from `20 m//s` to a value approaching zero at `s = 30 m,` determine the acceleration of the particle when `s = 15 m.`
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. At time `t = 0, s = -10 m.` Plot corresponding a-t and s-t graphs.
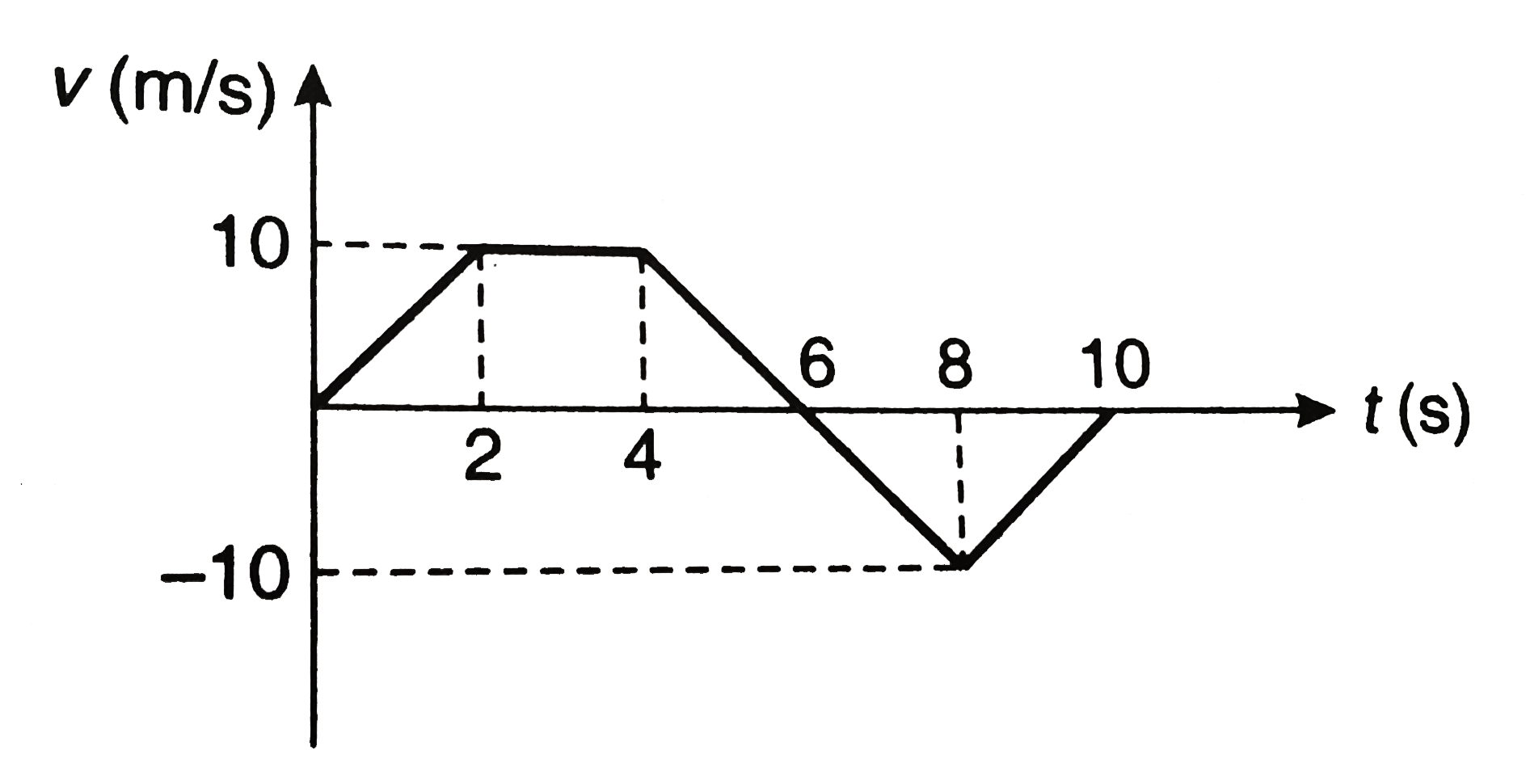
View SolutionA particle of mass m is released from a certain height h with zero initial velocity. It strikes the ground elastlcally (direction of its velocity is reversed but magnitude remains the same). Plot the graph between its kinetic energy and time till it returns to its initial position.
View SolutionA ball is dropped from a height of 80 m on a floor. At each collision, the ball loses half of its speed. Plot the speed-time graph and velocity-time graph of its motion till two collisions With the floor. [Take `g=10 m//s^2`]
View SolutionFigure shows the acceleration-time graph of a particle moving along a straight line. After what time the particle acquires its initial velocity?

View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. At time `t= 0,` displacement of the particle from mean position is 10 m. Find
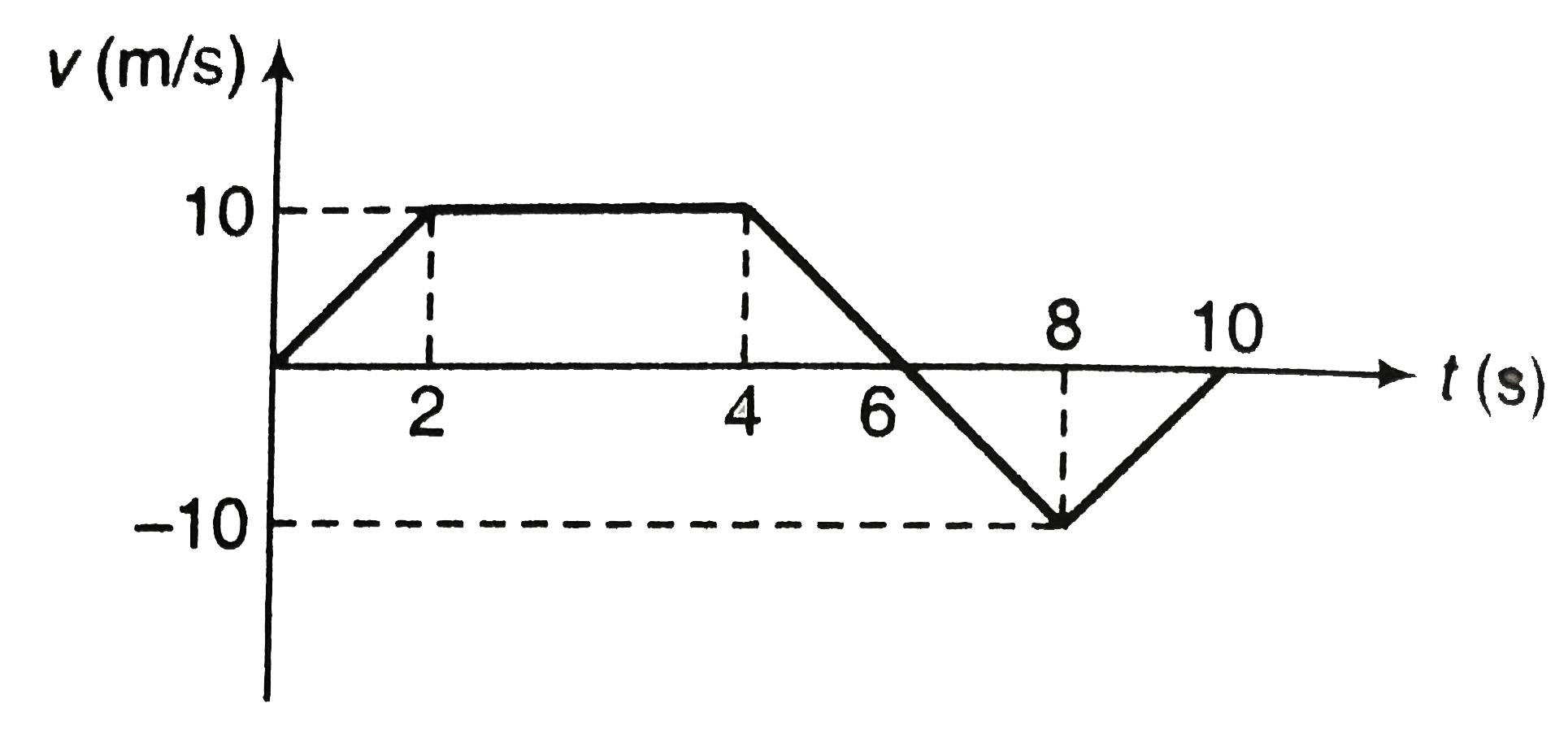
(a) acceleration of particle at `t = 1 s, 3 s and 9 s.`
(b) position of particle from mean position at `t = 10 s.`
(c) write down s-t equation for time interval (i)`0letle2s`, (ii) `4sletle8s`
View SolutionTwo particles 1 and 2 are thrown in the directions shown in figure simultaneously with velocities `5 m//s and 20 m//s.` Initially, particle 1 is at height 20 m from the ground. Taking upwards as the positive direction, find

(a) acceleration of 1 with respect to 2
(b) initial velocity of with respect to 1
(c) velocity of 1 with respect to 2 after time `t= 1/2 s`
(d) time when the particles will collide.
View SolutionA ball is thrown vertically upward from the 12 m level with an initial velocity of `18 m//s.` At the same instant an open platform elevator passes the 5 m level, moving upward with a constant velocity of `2 m//s.` Determine (`g = 9.8 m//s^2` )
(a) when and where the ball will meet the elevator,
(b) the relative velocity of the ball with respect to the elevator when the ball hits the elevator.
View SolutionAn automobile and a truck start from rest at the same instant, with the automobile initially at some distance behind the truck. The truck has a constant acceleration of `2.2 m//s^2` and the automobile has an acceleration of `3.5 m//s^2`. The automobile overtakes the truck when it (truck) has moved 60 m.
(a) How much time does it take the automobile to overtake the truck ?
(b) How far was the automobile behind the truck initially ?
(c) What is the speed of each during overtaking ?
View SolutionGiven `|V_br| = 4 m//s =` magnitude of velocity of boatman with respect to river, `v_r= 2 m//s` in the directior shown. Boatman wants to reach from point A to point B. At what angle `theta` should he row his boat ?
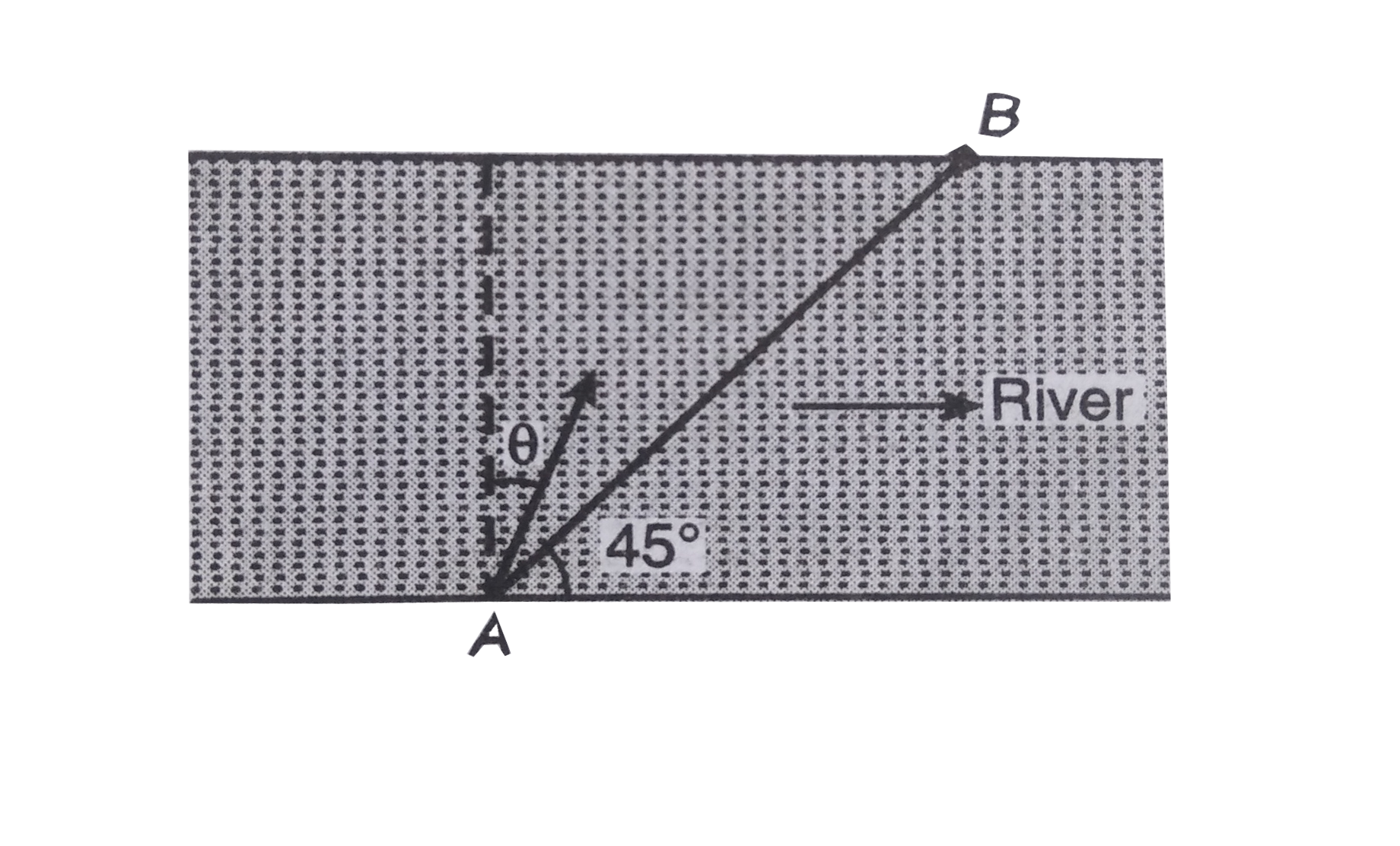
View SolutionAn aeroplane has to go from a point P to another point Q, 1000 km away due north. Wind is blowing due east at a speed of `200 km//h.` The air speed of plane is `500 km//h.`
(a) Find the direction in which the pilot should head the plane to reach the point Q.
(b) Find the time taken by the plane to go from P to Q.
View SolutionA train stopping at two stations 4 km apart takes 4 min on the journey from one of the station to the other. Assuming that it first accelerates with a uniform acceleration x and then that of uniform retardation y, prove that `1/x + 1/y = 2.`
View SolutionWhen a man moves down the inclined plane with a constant speed `5 ms^-1` which makes an angle of `37^@` with the horizontal, he finds that the rain is falling vertically downward. When he moves up the same inclined plane with the same speed, he finds that the rain makes an angle `theta = tan^-1 (7/8)` with the horizontal. The speed of the rain is
View SolutionEquation of motion of a body is `(dv)/(dt) = -4v + 8,` where v is the velocity in `ms^-1` and t is the time in second. Initial velocity of the particle was zero. Then,
View SolutionTwo particles A and B are placed in gravity free space at `(0, 0, 0) m and (30, 0, 0) m` respectively. Particle A is projected with a velocity `(5hat i + 10 hat j + 5 hat k) ms^-1,` while particle B is projected with a velocity `(10 hat i + 5 hat j + 5 hat k) ms^-1` simultaneously. Then,
View SolutionVelocity of the river with respect to ground is given by `v_0.` Width of the river is d. A swimmer swims (with respect to water) perpendicular to the current with acceleration `a = 2t` (where t is time) starting from rest from the origin O at `t= 0.` The equation of trajectory of the path followed by the swimmer is

View SolutionThe relation between time t and displacement x is `t = alpha x^2 + beta x,` where `alpha and beta` are constants. The retardation is
View SolutionA street car moves rectilinearly from station A to the next station B (from rest to rest) with an acceleration varying according to the law `f = a-bx,` where a and b are constants and x is the distance from station A. The distance between the two stations and the maximum velocity are
View SolutionA particle of mass m moves on positive x-axis under the influence of force acting towards the origin given by `-kx^2 hat i.` If the particle starts from rest at `x=a,` the speed it will attain when it crosses the origin is
View SolutionA partial along a straight line whose velocity-displacement graph is as shown in the figure. What is the magnitude of acceleration when displacement is 3 m ?
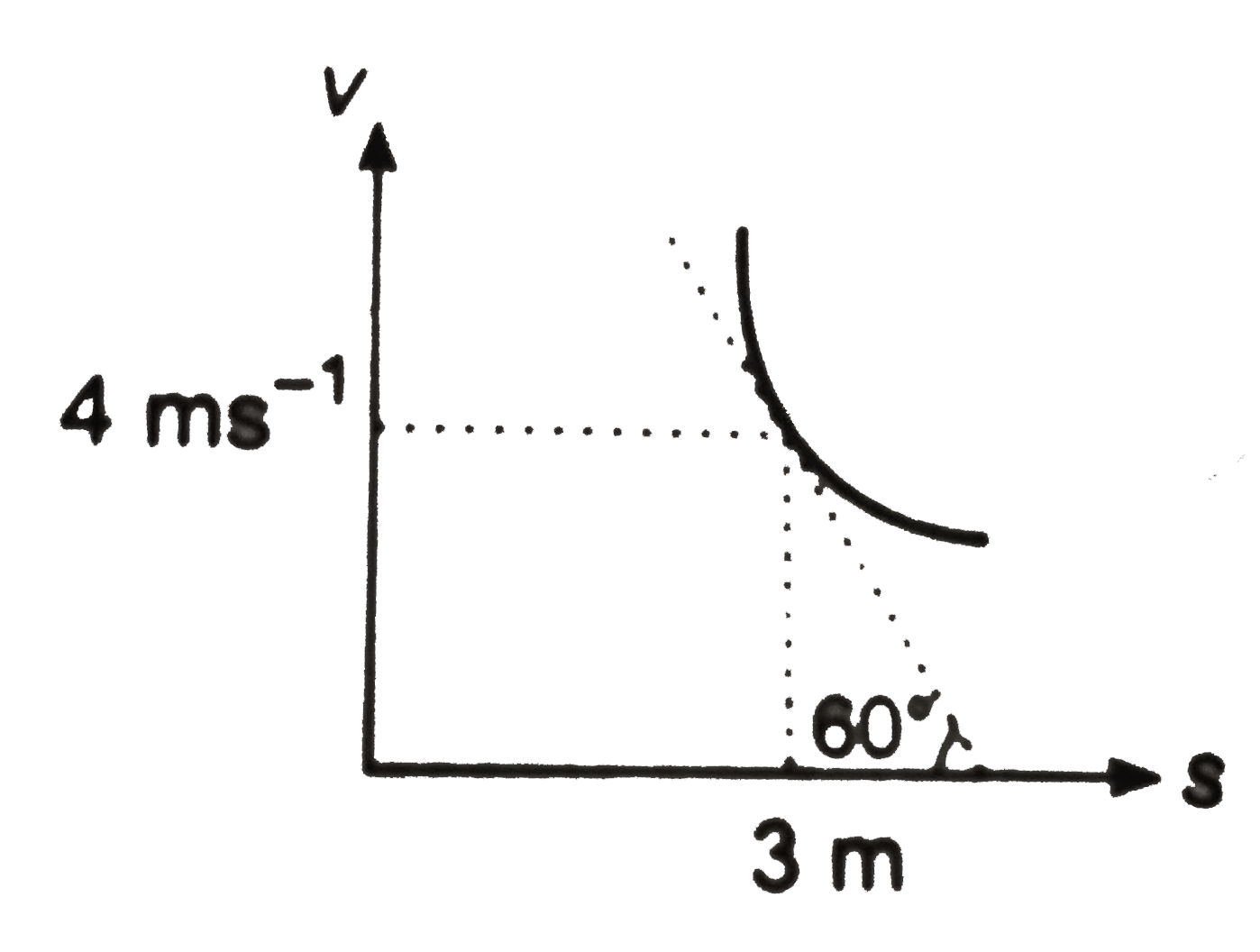
View SolutionA particle is falling freely under gravity. In first t second it covers distance `x_1` and in the next t second, it covers distance `x_2,` then t is given by
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity `2 ms^-1` towards right. The velocity of end B of rod at the instant shown in figure is
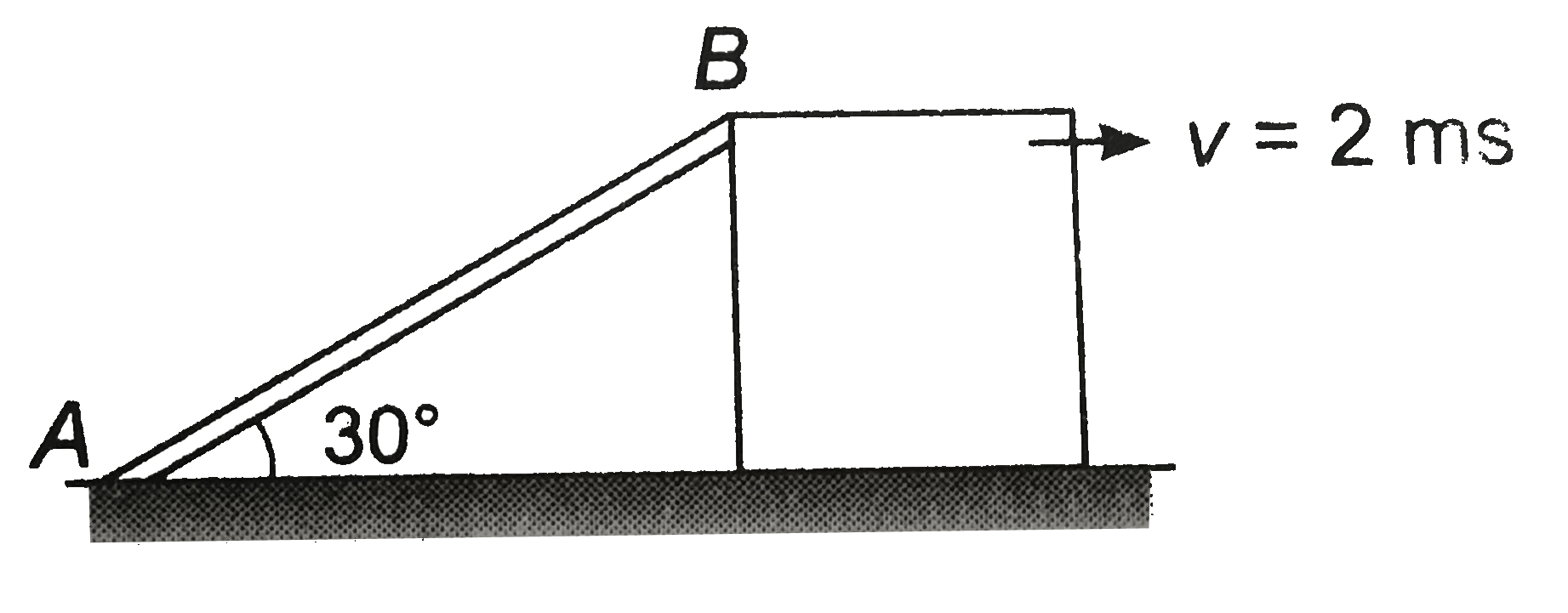
View SolutionA thief in a stolen car passes through a police check post at his top speed of `90 kmh^-1.` A motorcycle cop, reacting after 2 s, accelerates from rest at `5 ms^-2.` His top speed being `108 kmh^-1.` Find the maximum separation between policemen and thief.
View SolutionAnoop (A) hits a ball along the ground with a speed u in a direction which makes an angle `30^@` with the line joining him and the fielder Babul (B). Babul runs to intercept the ball With a speed `(2u)/3.` At What angle theta should he run to intercept the ball ?

View SolutionA car is travelling on a straight road. The maximum velocity the car Can attain is `24 ms^-1.` The maximum acceleration and deceleration it can attain are `1 ms^-2` and `4 ms^-2` respectively. The shortest time the car takes from rest to rest in a distance of 200 m is,
View SolutionA car is travelling on a road. The maximum velocity the car can attain is `24 ms^-1` and the maximum deceleration is `4 ms^-2.` If car starts from rest and comes to rest after travelling 1032m in the shortest time of 56 s, the maximum acceleration that the car can attain is
View SolutionTwo particles are moving along two long straight lines, in the same plane with same speed equal to `20 cm//s.` The angle between the two linse is `60^@` and their intersection point isO. At a certain moment, the two particles are located at distances 3m and 4m from O and are moving twowards O. Subsequently, the shortest distance between them will be
View SolutionA particle having a velocity `v = v_0` at `t= 0` is decelerated at the rate `|a| = alpha sqrtv ,` where `alpha` is a positive constant.
View SolutionAt time `t = 0,` a car moving along a straight line has a velocity of `16 ms^-1.` It slows down with an acceleration of `-0.5t ms^-2,` where t is in second. Mark the correct statement (s).
View SolutionAn object moves with constant acceleration a. Which of the following expressions are also constant?
View SolutionShip A is located 4 km north and 3 km east of ship B. Ship A has a velocity of `20 kmh^-1` towards the south and ship B is moving at `40 kmh^-1` in a direction `37^@` north of east. X and Y-axes are along east and north directions, respectively
View SolutionStarting from rest a particle is first accelerated for time `t_1` with constant acceleration `a_1` and then stops in time `t_2` with constant retardation `a_2.` Let `v_1` be the average velocity in this case and `s_1` the total displacement. In the second case it is accelerating for the same time `t_1` with constant acceleration `2a_1` and come to rest with constant retardation `a_2` in time `t_3.` If `v_2` is the average velocity in this case and `s_2` the total displacement, then
View SolutionA particle is moving along a straight line. The displacement of the particle becomes zero in a certain time `(tgt 0).` The perticle does not undergo any collision.
View SolutionA particle is resting over a smooth horizontal floor. At `t = 0,` a horizontal force starts acting on it. Magnitude of the force increases with time according to law `F = alpha t,` Where alpha is a positive constant. From figure, which of the following statements are correct ?
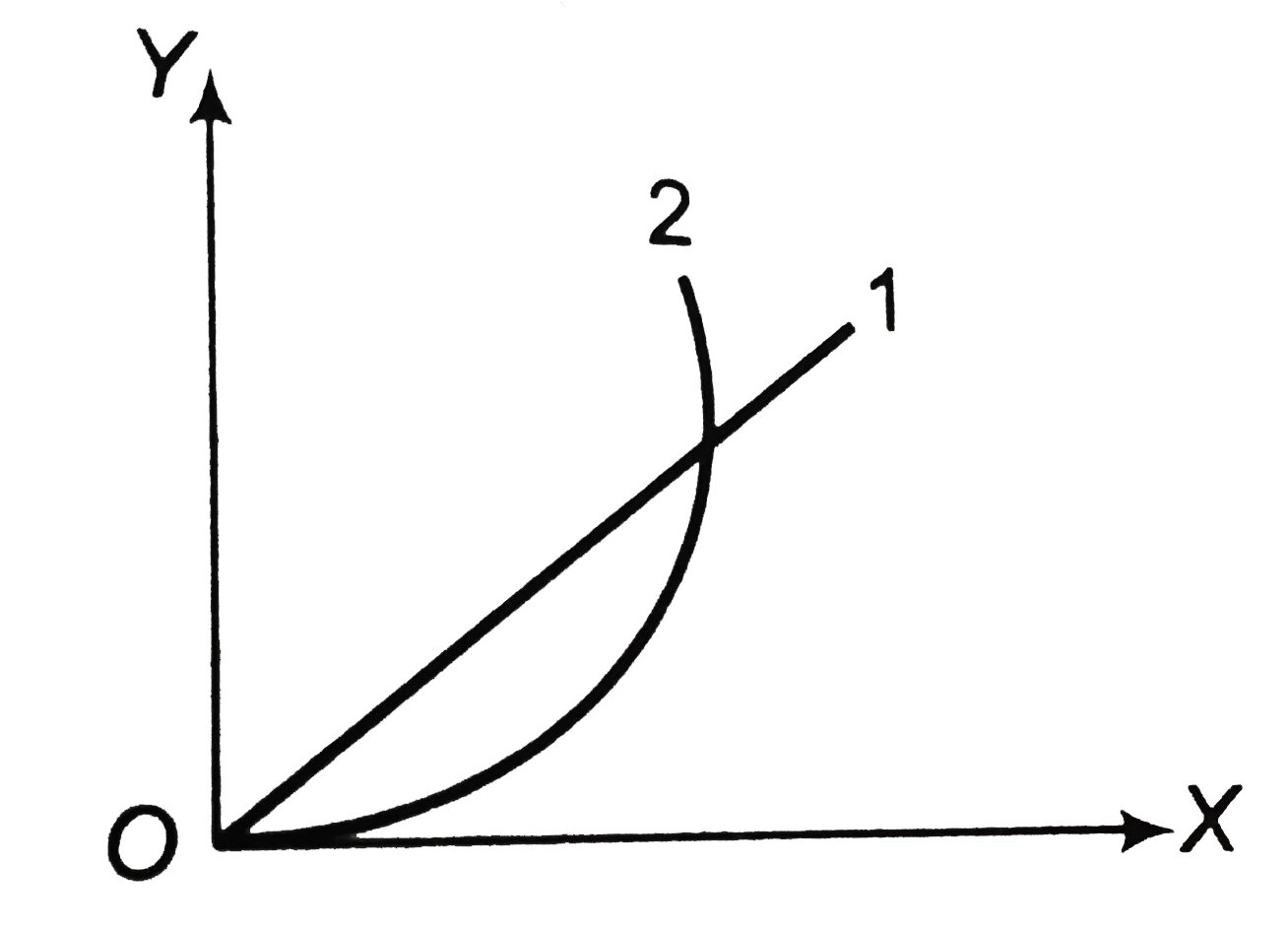
View SolutionA train starts from rest at `S = 0` and is subjected to an acceleration as shown in figure. Then,
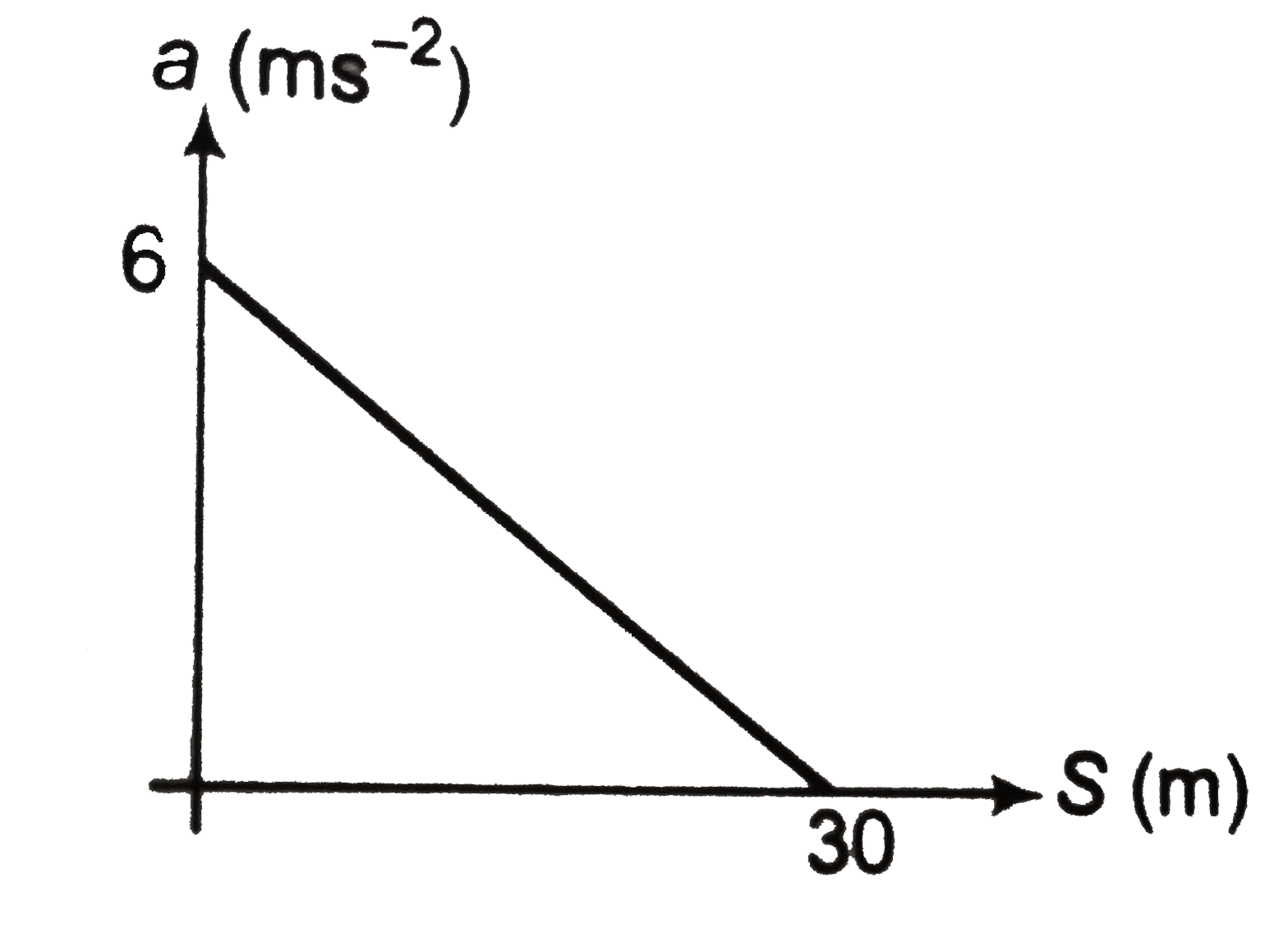
View SolutionFor a moving particle, which of the following options may be correct? Here, `V_(av)` is average velocity and `v_(av)` the average speed.
View Solution
Subjective questions and complete solutions for chapter KINEMATICS of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS KINEMATICS
- Assertion And Reason
- Comprehension
- COMPREHENSION_TYPE
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Exercise 6.1
- Exercise 6.2
- Exercise 6.3
- Exercise 6.4
- Exercise 6.5
- Exercise 6.6
- Exercise 6.7
- Exercise 6.8
- Exercise 6.9
- INTEGER_TYPE
- MATCH THE COLUMN
- MCQ_TYPE
- Miscellaneous Example
- More Than One Correct
- Objective
- SCQ_TYPE
- Subjective
- Subjective Questions