Complete Solutions to Subjective Questions of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| DC PANDEY | Subjective Questions |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
To test the quality of a tennis ball, you drop it onto the floor from a height of 4.00 m. It rebounds to a height of 2.00 m. If the ball is in contact with the floor for 12.0 ms, what is its average acceleration during that contact? Take `g= 98 m//s^2.`
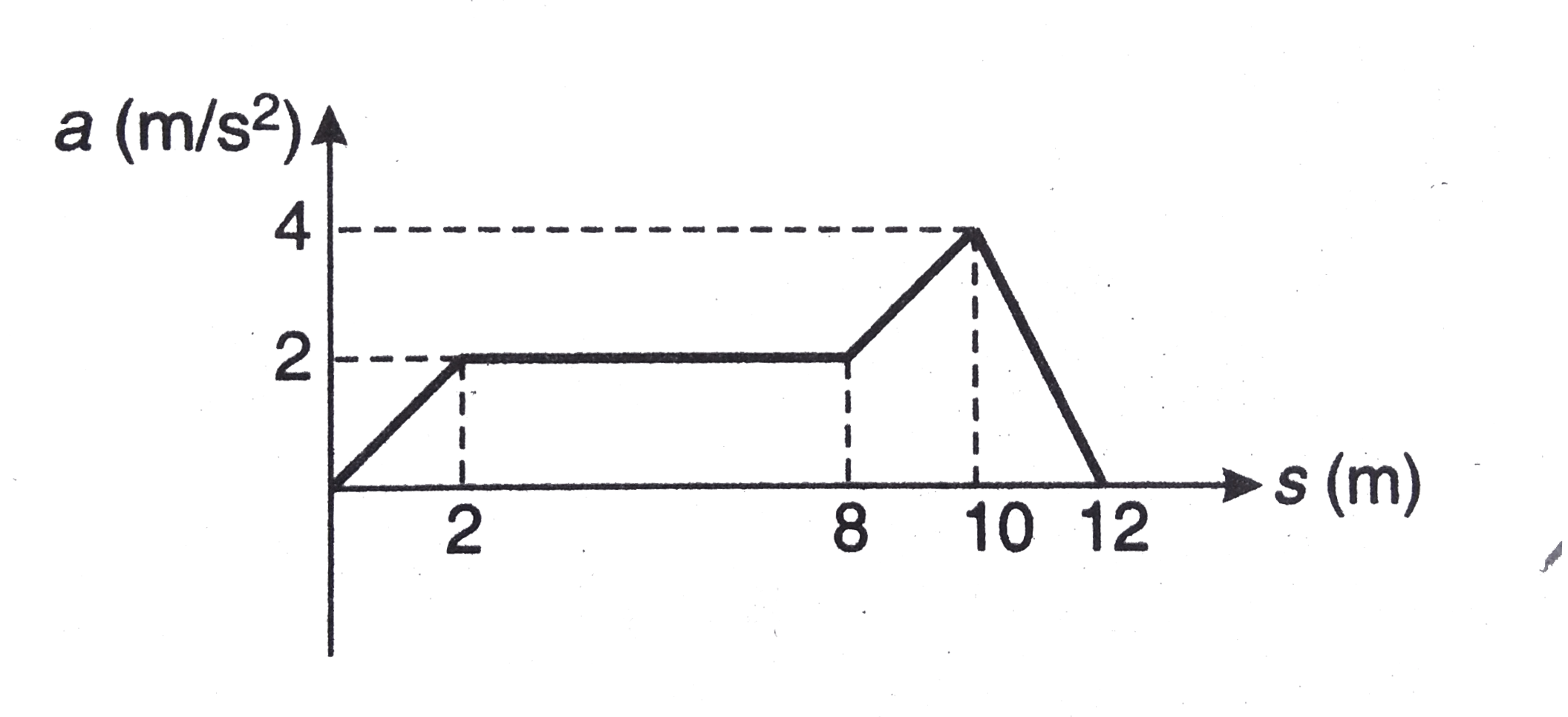
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is `s=12 m`.
View SolutionAt the initial moment three points A, B and C are on a horizontal straight line at equal distances from one another. Point A begins to move vertically upward with a constant velocity v and point C vertically downward without any initial velocity but with a constant acceleration a. How should point B move vertically for all the three points to be constantly on one straight line. The points begin to move simultaneously.
View SolutionA particle moves in a straight line with constant acceleration a. The displacements of particle from origin in times `t_1, t_2 and t_3 are s_1,s_2 and s_3` respectively. If times are in AP with common difference d and displacements are in GP, then prove that `a=((sqrt(s_1) - sqrt(s_3))^2)/d^2`
View SolutionA car is to be hoisted by elevator to the fourth floor of a parking garage, which is 14 m above the ground. If the elevator can have maximum acceleration of `0.2 m//s^2` and maximum deceleration of `0.1 m//s^2` and can reach a maximum speed of 2.5 m//s, determine the shortest time to make the lift, starting from rest and ending at rest.
View SolutionTo stop a car, first you require a certain reaction time to begin braking, then the car slows under the constant braking deceleration. Suppose that the total distance moved by your car during these two phases is 56.7 m when its initial Speed is 80.5 km//h and 24.4 m when its initial speed in 48.3 km//h. What are
(a) your reaction time and
(b) the magnitude or the deceleration?
View SolutionAn elevator without a ceiling is ascending with a constant speed of 10 m//s. A boy on the elevator shoots a ball directly upward, from a height of 2.0 m above the elevator floor. At this time the elevator floor is 28 m above the ground. The initial speed of the ball with respect to the elevator is 20 m//s. (Take `g=9.8m//s^2`)
(a) What maximum height above the ground does the ball reach?
(b) How long does the ball take to return to the elevator floor?
View SolutionA particle moves along a straight line and its velocity depends on time as `v = 3t - t^2.` Here, v is in `m//s` and t in second. Find
(a) average velocity and
(b) average speed for first five seconds.
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from `t = 2 s` to `t = 4 s.` Assume that `v = 0` at `t = 0.`
View SolutionA man wishes to cross a river of width 120 m by a motorboat. His rowing speed in still water is `3 m//s` and his maximum walking speed is `1m//s`. The river flows with velocity of `4 m//s`.
(a) Find the path which he should take to get to the point directly opposite to his starting point in the shortest time.
(b) Also, find the time which he takes to reach his destination.
View SolutionThe current velocity of river grows in proportion to the distance from its bank and reaches the maximum value `v_0` in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.
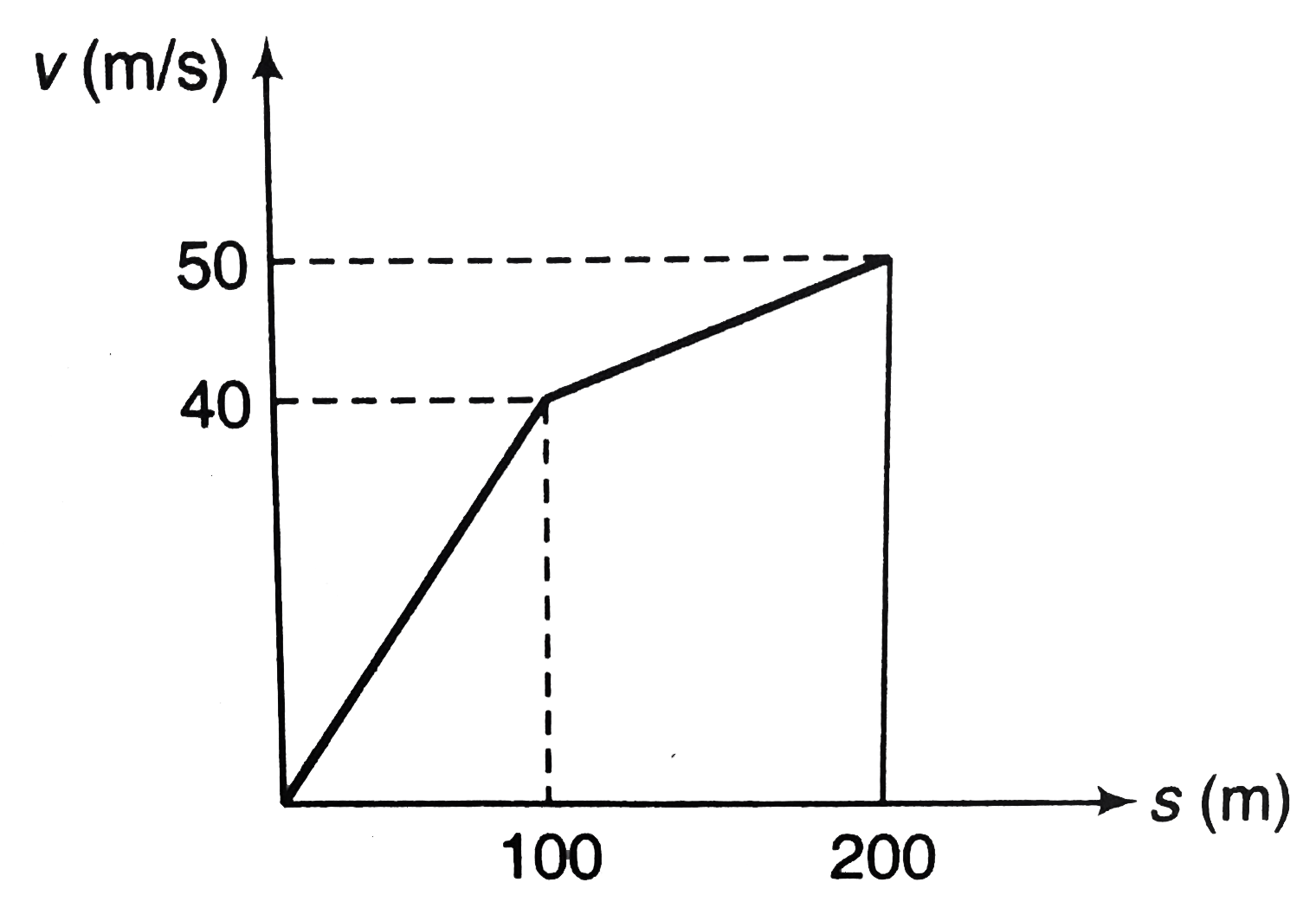
View SolutionThe v-s graph for an airplane travelling on a straight runway is shown. Determine the acceleration of the plane at `s = 50 m` and `s = 150 m`. Draw the a-s graph.
View SolutionA river of width a with straight parallel banks flows due north with speed u. The points O and A are on opposite banks and A is due east of O. Coordinate axes `O_x` and `O_y` are taken in the east and north directions respectively. A boat, whose speed is v relative to water, starts from O and crosses the river. If the boat is steered due east and u varies with `x as : u = x(a-x) v/a^2.` Find
(a) equation of trajectory of the boat,
(b) time taken to cross the river,
(c) absolute velocity of boatman when he reaches the opposite bank,
(d) the displacement of boatman when he reaches the opposite bank from the initial position.
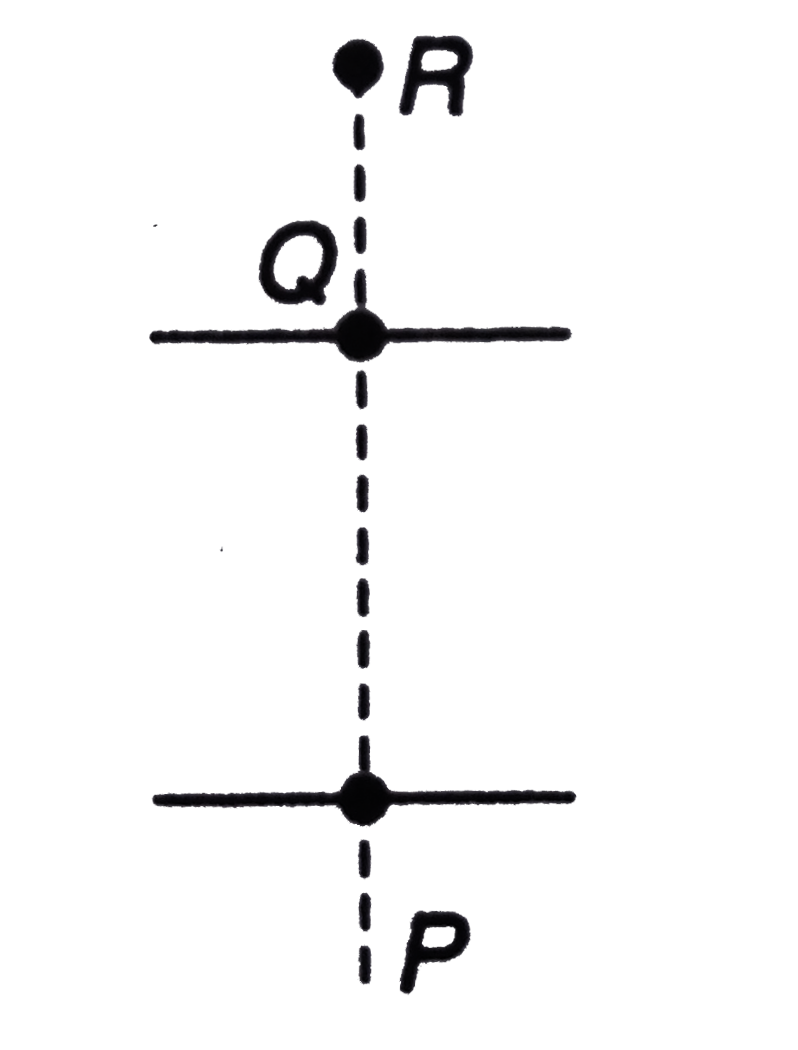
View SolutionA river of width `omega` is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If `PQ=QR=omega,` find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river.
View SolutionThe v-s graph describing the motion of a motorcycle is shown in figure. Construct the a-s graph of the motion and determine the time needed for the motorcycle to reach the position `s=120 m.` Given In `5 = 1.6.`

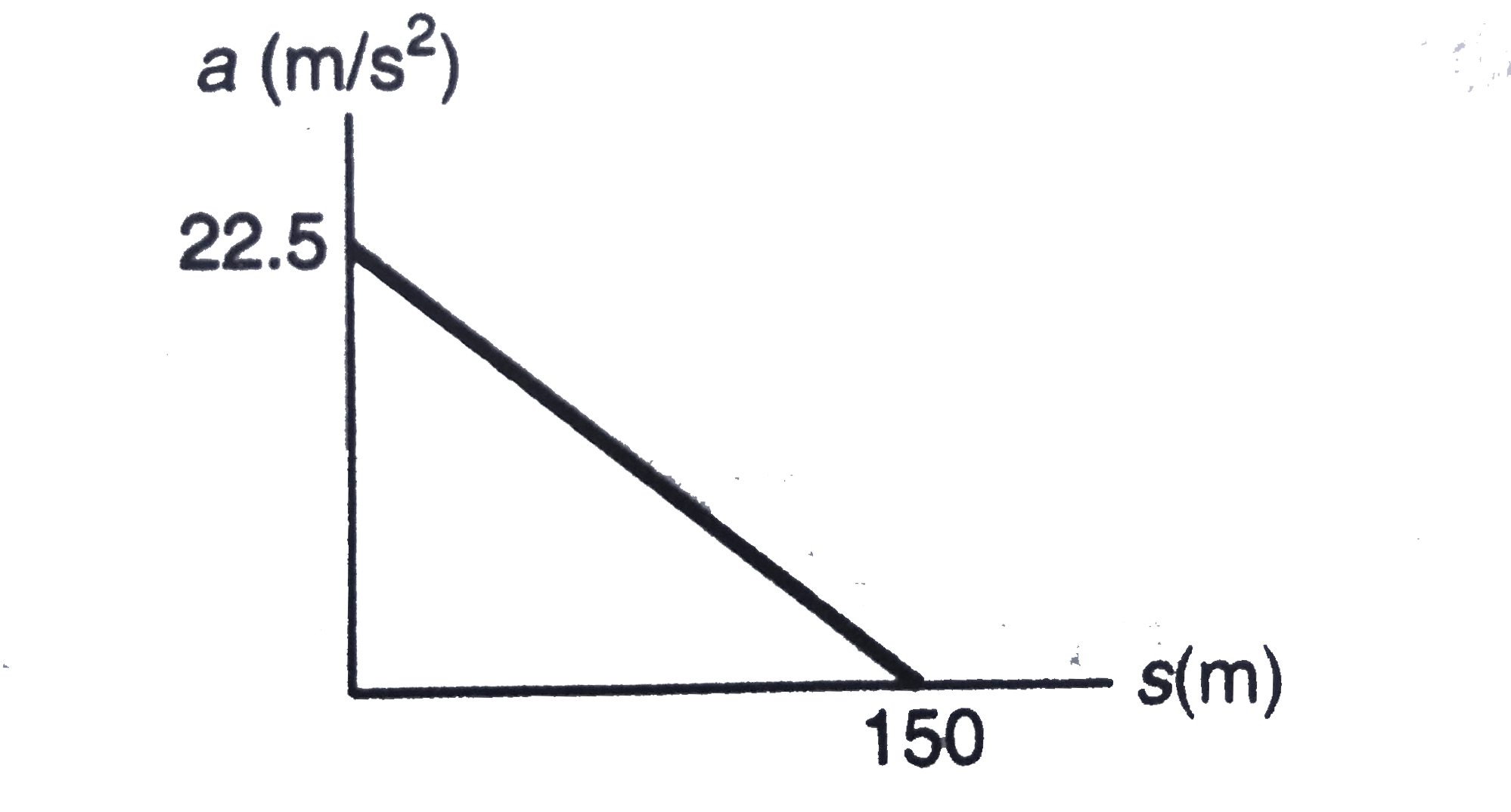
View SolutionThe jet plane starts from rest at `s =0` and is subjected to the acceleration shown. Determine the speed of the plane when it has travelled 60 m.
View SolutionA particle leaves the origin with an initial velodty `v= (3.00 hati) m//s` and a constant acceleration `a= (-1.00 hati-0.500 hatj) m//s^2.` When the particle reaches its maximum x coordinate, what are
(a) its velocity and (b) its position vector?
View SolutionThe Speed Of a particle moving in a plane is equal to the magnitude of its instantaneous velocity, `v=|vl= sqrt(v_x^2+v_y^2).`
(a) Show that the rate of change of the speed is `(dv)/(dt)=(v_xa_x+v_ya_y)/(sqrt(v_x^2+v_y^2))`.
(b) Show that the rate of change of speed can be expressed as `(dv)/(dt)` is equal to`a_t` the component of a that is parallelto v.
View SolutionA man with some passengers in his boat, starts perpendicular to flow of river 200 m wide and flowing with `2 m//s.` Speed of boat in still water is `4 m//s.` When he reaches half the width of river the passengers asked him that they want to reach the just opposite end from where they have started.
(a) Find the direction due which he must row to reach the required end.
(b) How many times more time, it would take to that if he would have denied the passengers?
View SolutionA child in danger of drowning in a river is being carried downstream by a current that flows uniformly at a speed of `2.5 km//h.` The child is 0.6 km from shore and 0.8 km upstream of a boat landing when a rescue boat sets out. If the boat proceeds at its maximum speed of `20 km//h` with respect to the water, what angle does the boat velocity v make with the shore? How long will it take boat to reach the child?
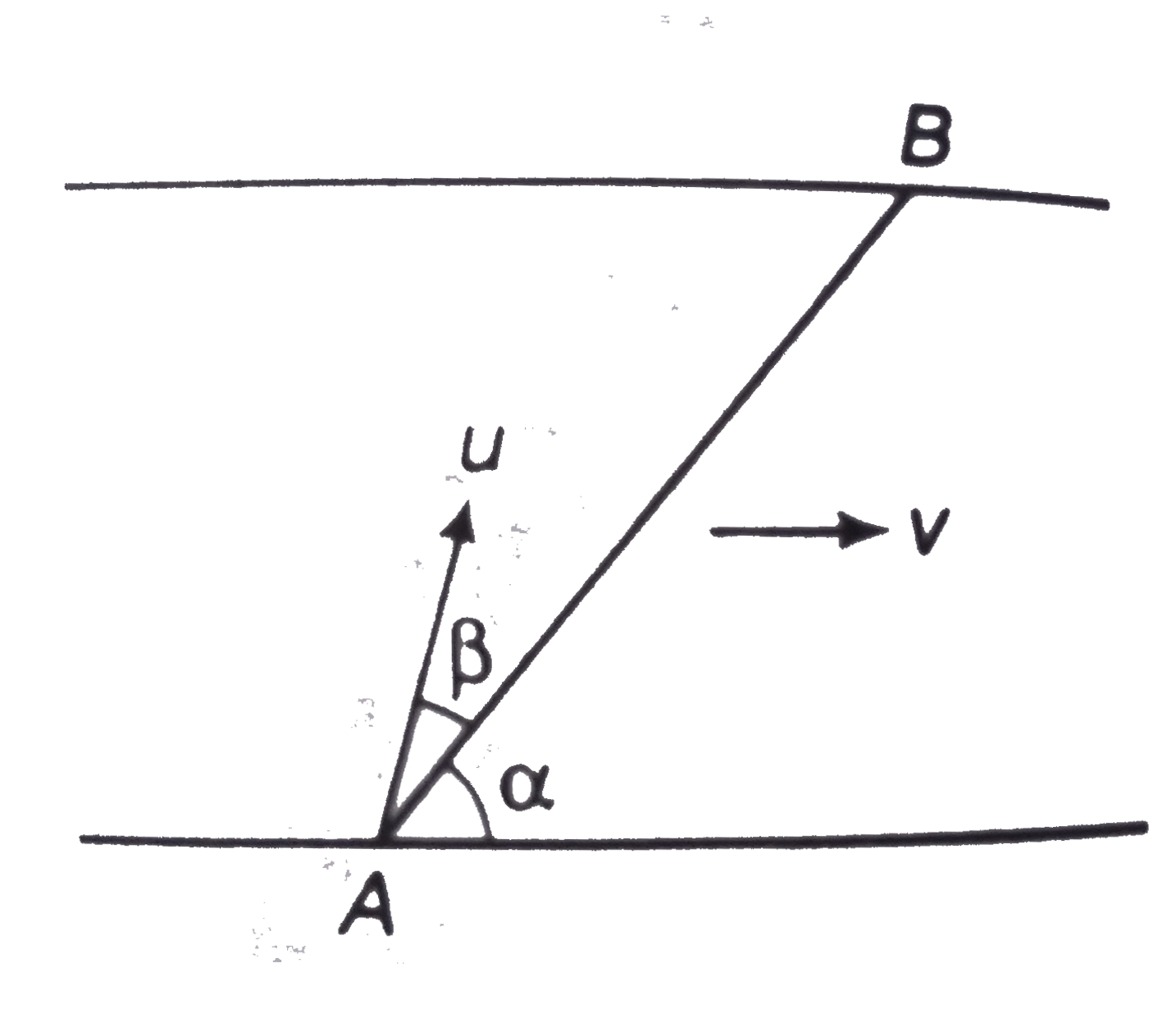
View SolutionA launch plies between two points A and B on the opposite banks of a river always following the line AB. The distance S between points and B is 1200 m. The velocity of the river current `v= 1.9 m//s` is constant over the entire width of the river. The line AB makes an angle `alpha= 60^@` with the direction of the current. With what velocity u and at what angle beta to the line AB should the launch move to cover the distance AB and back in a time `t= 5 min`? The angle beta remains the same during the passage from A to B and from B to A.
View SolutionThe slopes of wind screen of two cars are `alpha_1=30^@ and alpha_2= 15^@` respectively. At what ratio `v_1/ v_2` of the velocities of the cars will their drivers see the hail stones bounced back by the wind screen on their cars in vertical direction? Assume hail stones fall vertically downwards and collisions to be elastic.
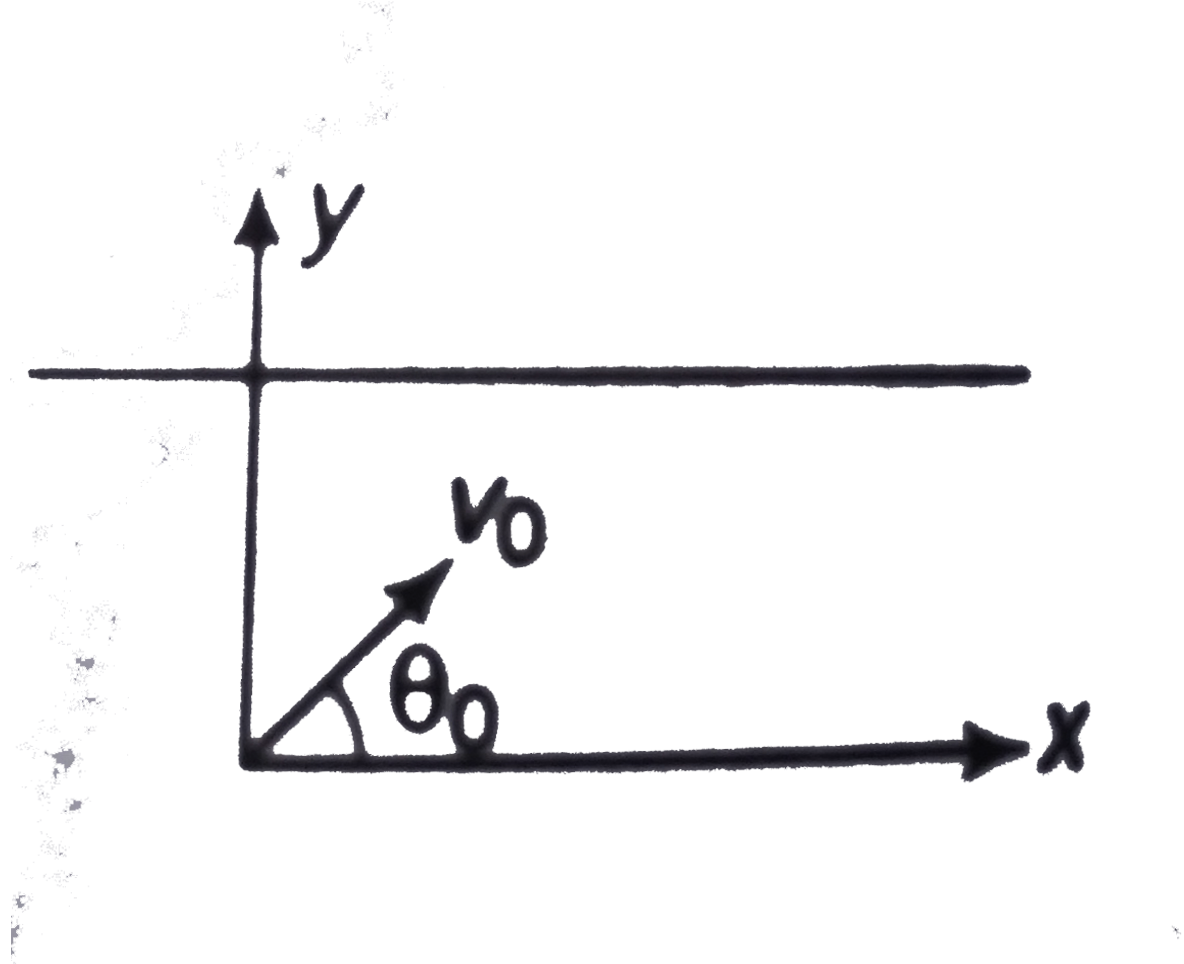
View SolutionA projectile of mass m is fired into a liquid at an angle `theta_0` with an initial velocity `v_0` as shown. If the liquid develops a frictional or drag resistance on the projectile which is proportional to its velocity, i. e. `F= -kv` where k is a positive constant, determine the x and y components of its velocity at any instant. Also find the maximum distance `x_(max)` that it travels?
View SolutionA man in a boat crosses a river from point A. If he rows perpendicular to the banks he reaches point C `(BC = 120 m)` in 10 min. If the man heads at a certain angle `alpha` to the straight line AB (AB is perpendicular to the banks) against the current he reaches point B in 12.5 min. Find the width of the river w, the rowing velocity u, the speed of the river current v and the angle `alpha`. Assume the velocity of the boat relative to water to be constant and the same magnitude in both cases.

View Solution
Subjective Questions questions and complete solutions for chapter KINEMATICS of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS KINEMATICS
- Assertion And Reason
- Comprehension
- COMPREHENSION_TYPE
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Exercise 6.1
- Exercise 6.2
- Exercise 6.3
- Exercise 6.4
- Exercise 6.5
- Exercise 6.6
- Exercise 6.7
- Exercise 6.8
- Exercise 6.9
- INTEGER_TYPE
- MATCH THE COLUMN
- MCQ_TYPE
- Miscellaneous Example
- More Than One Correct
- Objective
- SCQ_TYPE
- Subjective
- Subjective Questions