Complete Solutions to Subjective Question of chapter LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | LAWS OF MOTION |
| DC PANDEY | Subjective Question |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
A small marble is projected with a velocity of `10 m//s` in a direction `45^(@)`from the y-direction on the smooth inclined plane. Calculate the magnitude `v` of its velocity of after `2 s` (Take `g = 10 m//s^(2))`
 03:22View Solution
03:22View SolutionDetermine the acceleration of the `5 kg` block `A` . Neglect the mass of the pulley and cords . The block `B` has a mass of `10 kg`, The coefficient of kinetic friction between block `B` and the surface is `mu _(k) = 0.1` (take `g = 10 m//s^(2))`
 04:03View Solution
04:03View SolutionA `30 kg` mass is intially at rest on floor of a truck . The coefficient of static friction between the mass and the floor of truck in `0.3` and coefficient of kinetic friction is `0.2` . Intially the truck is travelling due east at constant speed.Find the magnitude and direction of the friction force acting on the mass , if : (take `g = 10 m//s^(2))`
(a) the truck acdceleration at `1.8 m//s^(2)` eastward
(b) the truck acdceleration at `3.8 m//s^(2)` westward03:50View SolutionA `6 kg` block `B` rests as shown on the upper surface of a `15 kg` wedge `A` . Neglecting friction , determine immadiately after the system is released from rest (a) the acceleration of `A` (b) the acceleration of `B` relative to `A` (take `g = 10 m//s^(2))`
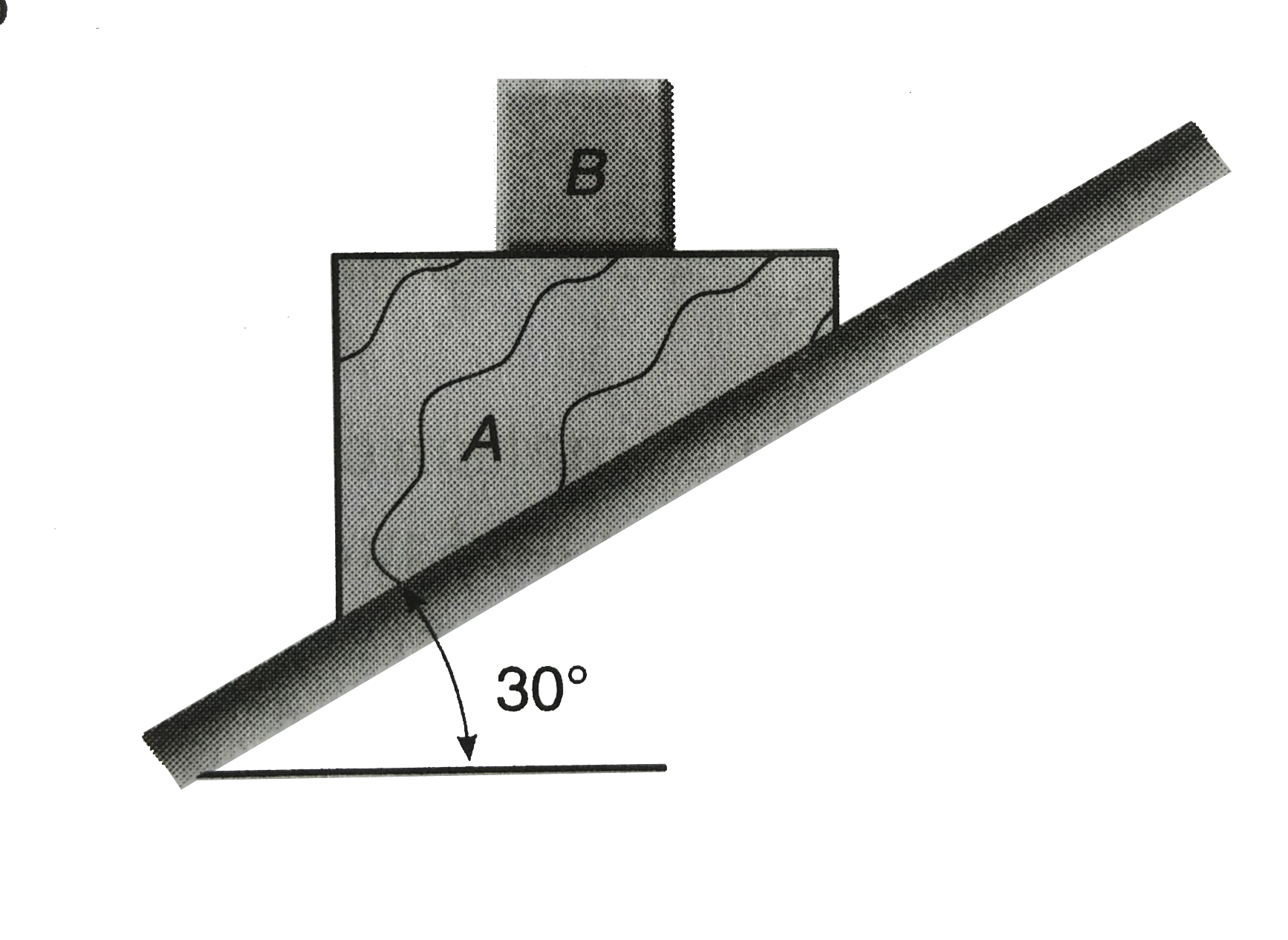 05:08View Solution
05:08View SolutionIn the arrangement shown in figure, the rod of mass `m` held by two smooth walls, remains always perpendicular to the surface of the wedge of mass `M`. Assuming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.
 05:03View Solution
05:03View SolutionAt the bottom edge of a smooth wall, an inclined plane is kept at an angle of `45^@`. A uniform ladder of length `l` and mass `M` rests on the inclined plane against the wall such that it is perpendicular to the incline.
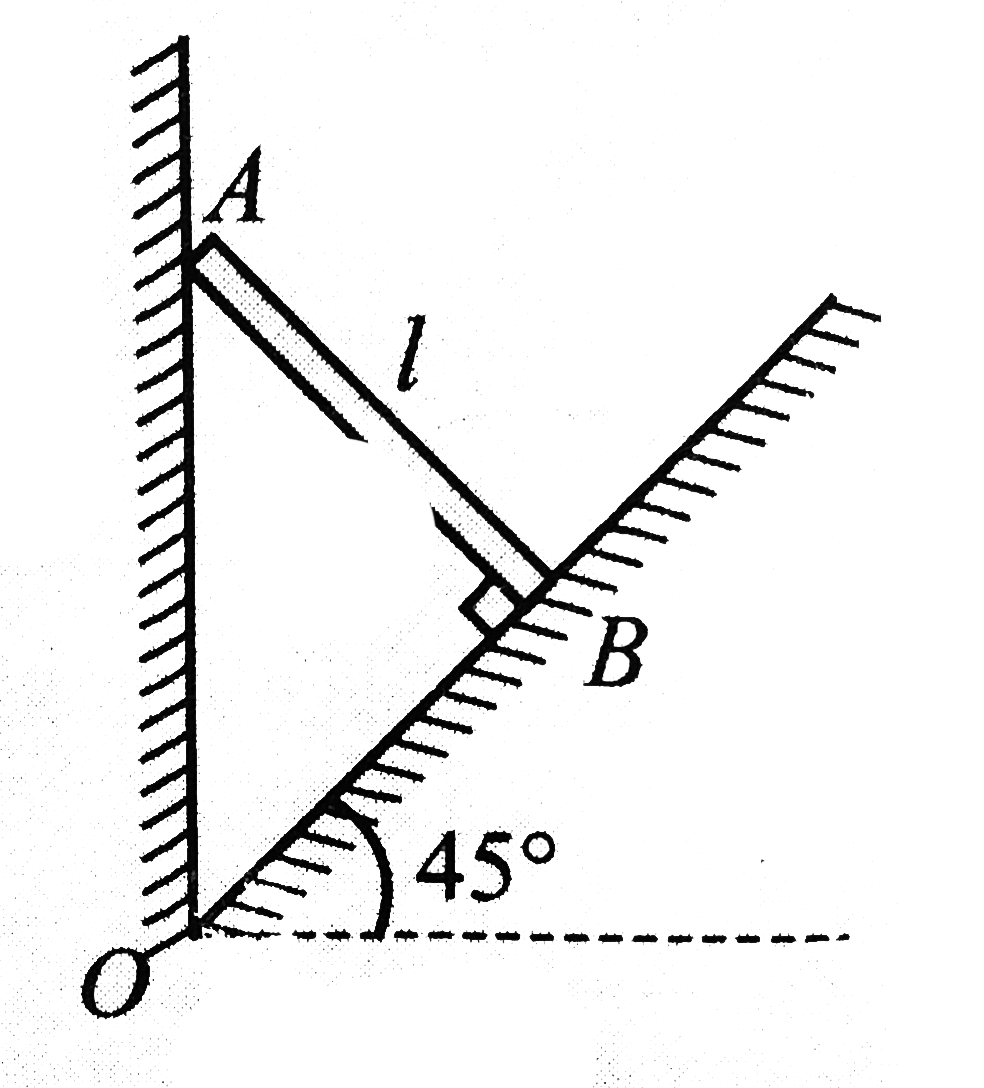
a. If the plane is also smooth, which way will the ladder slide?
b. What is the minimum coefficient of friction necessary so that the ladder does not slip on the incline.06:12View SolutionA plank of mass `M` is placed on a rough horizontal surface and a contant horizontal force `F` is applied on it . A man of mass `m` runs on the plank find the range of acceleration of the man that the plank does not move on the surface is `mu` .Assume that the does not slip on the plank
 05:33View Solution
05:33View SolutionFind the acceleration of two masses as shown in figure . The pulley are light and frictionless and string are light and frictionless and string are light and inextensible.
 04:09View Solution
04:09View SolutionThe upper portion of an inclined plane of inclination a is smooth and the lower portion is rough. A partical slide down from rest the top and just comes to rest at the foot . If the ratio of smooth length to rough length is `m:n`, find the coefficient of friction .
08:03View SolutionBlock `B` rests on surface . If the coefficient of static friction between `A` and `B` is `mu = 0.4`. Determine the acceleration of each , if
(a) `F = 30 N` and
(b) `F = 250 N (g = 10 m//s^(2))`
 07:16View Solution
07:16View SolutionBlock B has mass m and is released from rest when it is on top of wedge A, which has a mass 3m. Determine the tension in cord CD needed to hold the wedge from moving while B is sliding down A. Neglect friction.
 03:57View Solution
03:57View SolutionCoefficient of friction between the flat bad of the truck and crate are `mu = 0.8 and mu_(k) = 0.7`. The coefficient of kinetic friction between the truck tires and the road surface is `0.9` .If the truck stops from an initial speed of `15 m//s` with maximum braking (wheels skidding). Determine where on the bed the crate finally comes to rest. (take `g = 10 m//s^(2))`
 05:49View Solution
05:49View SolutionThe `10 kg` block is moving to the left with a speed of `1.2 m//s` at time `t = 0` A force `F` is applied kinetic friction is `mu_(k) = 0.2`. Determine the time `t` at which the block comes to a slip. `(g = 10 m//s^(2))`
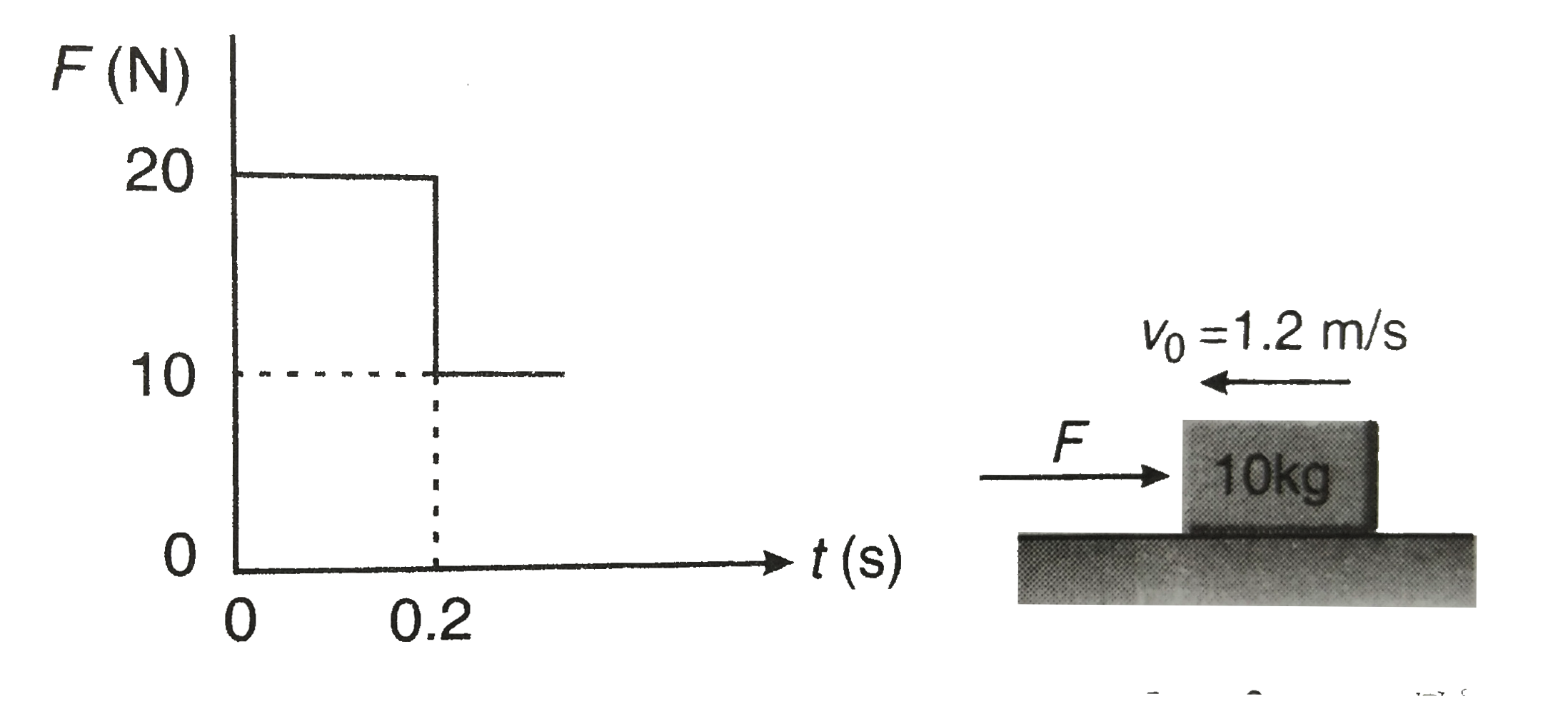 05:24View Solution
05:24View SolutionThe `10 kg` block is resting on the horizontal surface when the force `F` is applied to it for `7 s` . The variation of `F` with time is shown . Calculate the maximum velocity reached by the block and the total time `t` during which the block is in motion. The coefficient of static and kinetic friction are both `0.50.(g = 9.8 m//s^(2))`
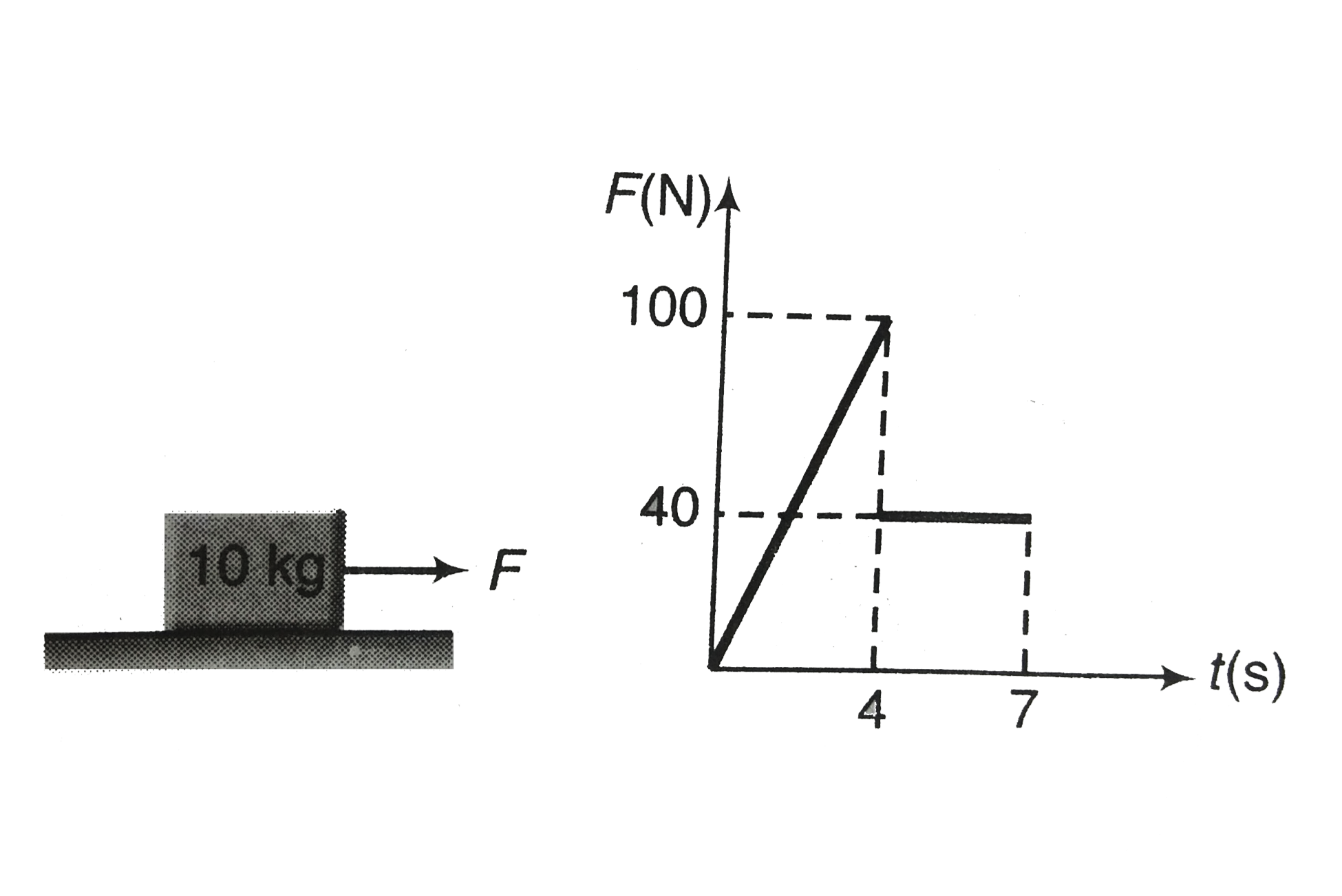 08:10View Solution
08:10View SolutionIf block `A` of the pulley system is moving downward with a speed of `1 m//s` while block `C` moving up at `0.5m//s` determine the speed of block `B`
 02:51View Solution
02:51View SolutionThe collar `A` is free to slide along the smooth shaft `B` mounted in the frame. The plane of the frame is the vertical . Determine the horizontal acceleration a of the frame necessary to maintain the collar in a fixed position on the shaft. `(g = 9.8 m//s^(2))`
 04:24View Solution
04:24View SolutionIn the adjoining figure all surface are frictionless . What force `F` must by applied to `M_(1)` to keep `M_(3)` free from rising or falling?
 02:57View Solution
02:57View SolutionThe converyor belt is designed to transport packges of verious weights.Each `10 kg` package has a coefficient of kinetic friction `mu_(k) = 0.15`.If the speed of the conveyor belt is `5 m//s` and then it suddenly stops, determine the distance the package will slide before coming to rest `(g = 9.8 m//s^(2))`
 02:33View Solution
02:33View SolutionA block of mass `m` slides down an inclined right angled trough .If the coefficient of friction between block and the trough is `mu_(k)` acceleration of the block down the plane is
 03:22View Solution
03:22View SolutionA heavy chain with a mass per unite length `p` is pulled by the constant force `F` along a horizental surface consisting of a smooth section and a rough section. The chain is initially at rest on the rough surface with `x = 0` . If the coefficient of kinetic friction between the chain and the rough surface is `mu_(k)` determine the velocity `v` of the chain when `x = L` . The force `F` is hreater than `mu_(k) ogL` in under to initate the motion ,
 05:34View Solution
05:34View SolutionA package rest on a conveyor belt which is initially at rest . The belt is started and moves to the right for `1.3 s` with a constant acceleration of `2 m//s^(2)`. The belt then moves with a constant deceleration `a_(2)` and comes to a stop after a total displacement of `2.2 m` . Knowing that the coefficient of friction between the package and the belt are `mu_(s) = 0.35` and `mu_(k) = 0.25` , determine (a) the deceleration `a_(2)` of the belt , (b) the displacement of the package relative to the belt as the belt comes to a stop. `(g = 9.8 m//s^(2))`
 06:43View Solution
06:43View SolutionDetermine the normal force the `10 kg` crate `A` exerts on the smooth cart `B` , if the cart is given an acceleration of `a = 2 m//s^(2)` down the plane . Also find the acceleration of the crate . Set `theta = 30^(@) (g = 10 m//s^(2))`
 02:31View Solution
02:31View SolutionA small block of mass `m` is projected on a larger block of mass `10 m` and length `l` with a velocity `v` as shown in the figure. The coefficient of friction between the two block is `mu_(2)` while that between the lower block and the ground is `mu_(1)`. Given that `mu_(2) gt 11 mu_(1)`.

(a) Find the minimum value of `v`, such that the mass `m` falls off the block of mass `10 m` .
(b) If `v` has minimum value, find the time taken by block `m` to do so.07:19View SolutionA partical of mass `m` and velocity `v_(1)` in positive y direction is projected on to a belt that is moving with uniform velocity `v_(2)` in x- direction as shown in figure. Coefficient of friction between partical and belt is `mu` . Assuming that the partical first touches the belt at the origin of fixed `x-y` coordinate system and remains on the belt , find co-ordinates `(x-y)` of the point where slidding stop.
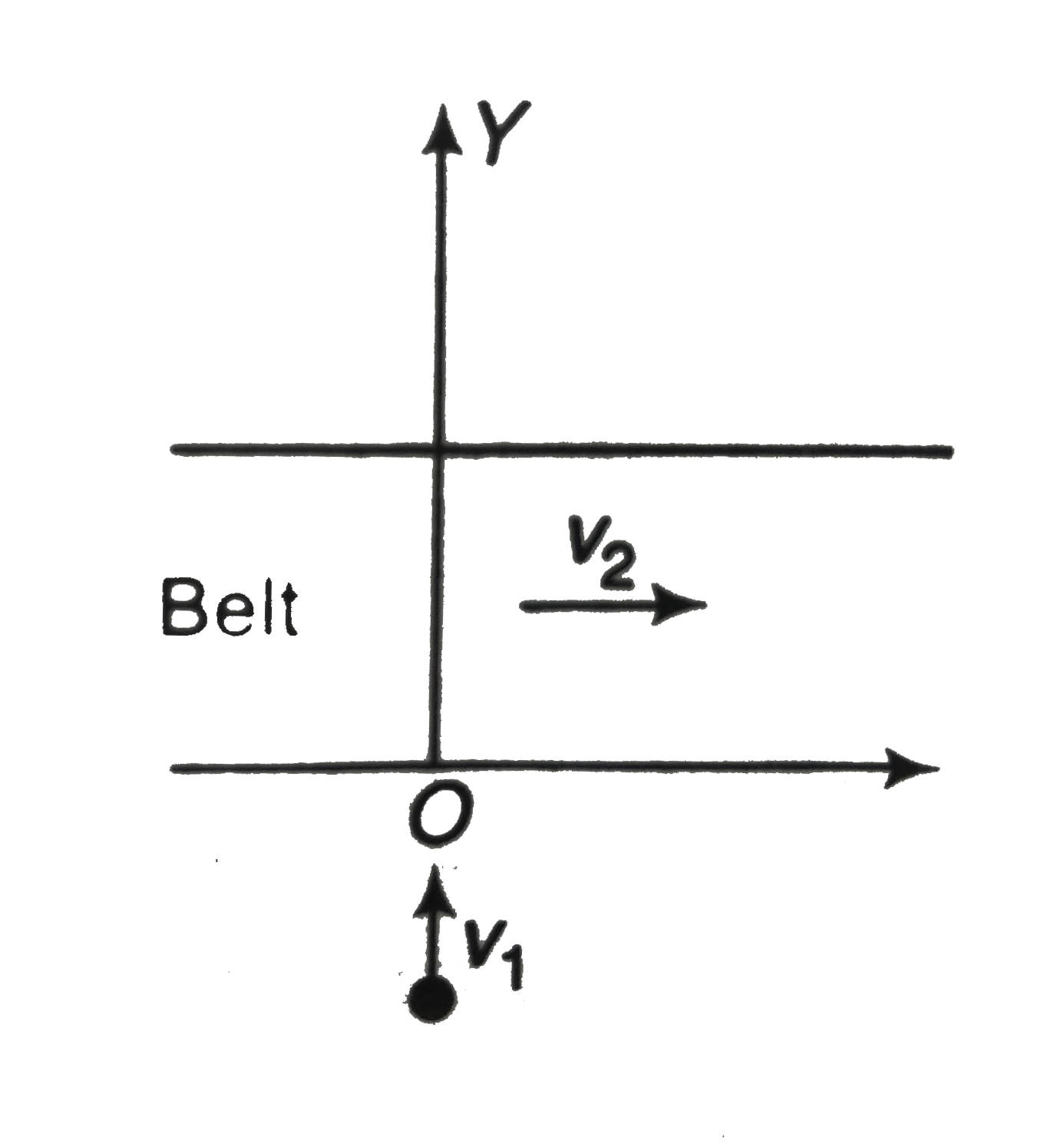 08:51View Solution
08:51View SolutionIn the shown arrangement , both pulleys and the string are massless and all the surface are frictionless. Find the acceleration of the wedge.
 05:21View Solution
05:21View SolutionNeglect friction. Find acceleration of `m, 2 m and 3 m` as shown in the figure. The wedge is find.
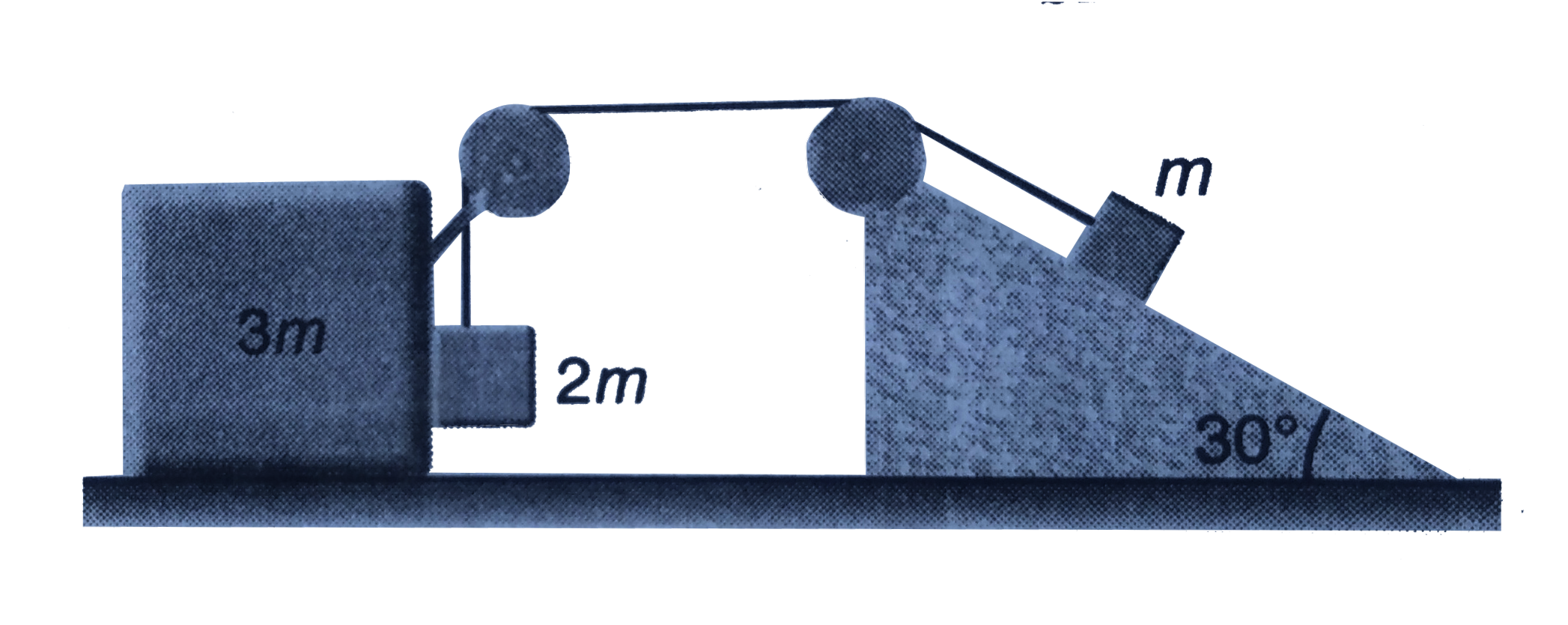 06:49View Solution
06:49View SolutionThe figure an `L` shaped body of mass `M` placed on smooth horizontal surface. The block `A` is connected to the body by means of an inexiensible string , which is passing over a smooth pulley of negligible mass.Another block `B` of mass `m` is placed against a vertical wall of the body. Find the minimum value of the mass of block `A` so that `B` remain stationary relative to the wall. Coefficient of friction between the block `B` and the vertical wall is `mu`.
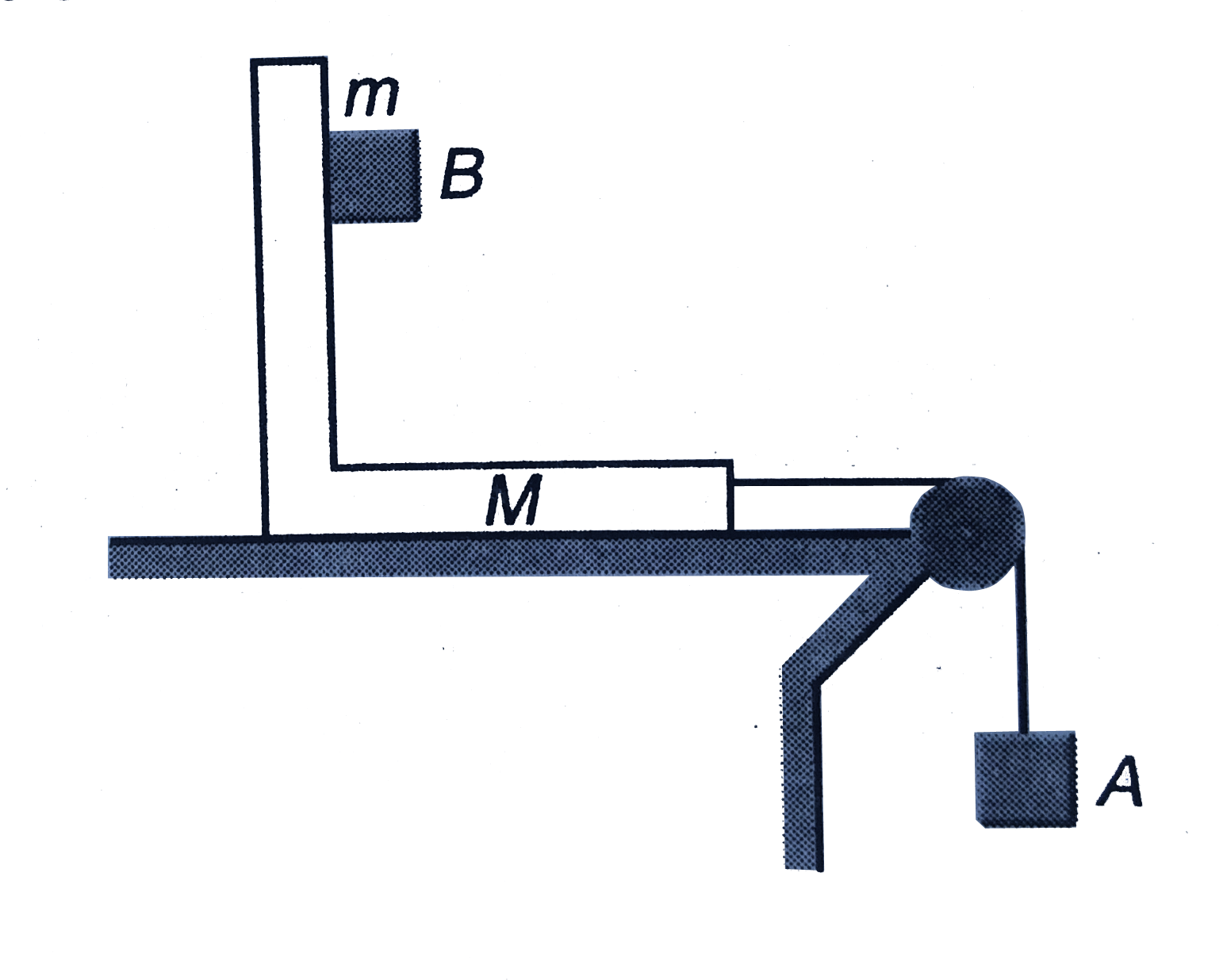 03:40View Solution
03:40View Solution
Subjective Question questions and complete solutions for chapter LAWS OF MOTION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS LAWS OF MOTION
- Chapter exercises (A) Taking it together
- Check point 5.1
- Check point 5.2
- Check point 5.3
- Check point 5.4
- Comprehension
- Exercise 8.1
- Exercise 8.2
- Exercise 8.3
- Exercise 8.4
- Exercise 8.5
- Match the columns
- Medical entrances gallery
- Miscellaneous Examples
- Objective Question
- Single Correct
- Solved Examples
- Subjective Question
