Complete Solutions to Chapter exercises (A) Taking it together of chapter LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | LAWS OF MOTION |
| DC PANDEY NEET | Chapter exercises (A) Taking it together |
| Number Of Questions | 71 |
| Academic Year | 2023-24 |
A ball is travelling with uniform translatory motion. This means that
View SolutionA metre scale is moving with uniform velocity. This implies .
View SolutionConservation of momentum in a collision between particles can be understood from
View SolutionA hockey player is moving northward and suddenly turns westward with the same speed to avoid an opponet. The force that acts on the player is.
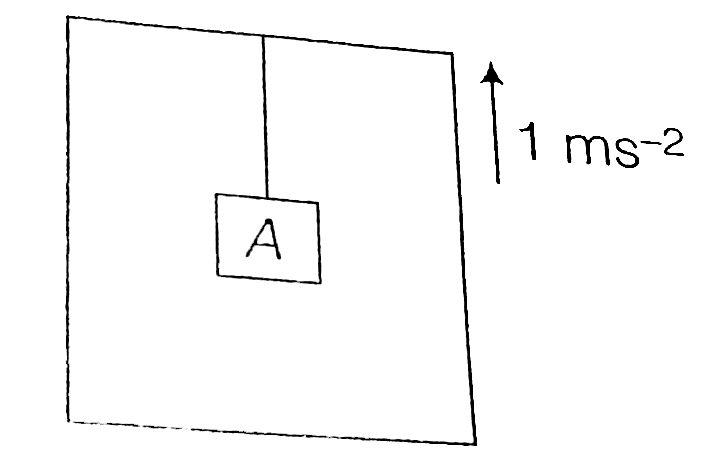
View SolutionIf the elevator in shown figure is moving upwards with constant acceleration `1 ms^(-2)`, tension in the string connected to block A of mass 6 kg would be ( take, g`=10 ms^(-2)`)
View SolutionA block can slide on a smooth inclined plane of inclination `theta` kept on the floor of a lift. When the lift is descending with a retardation a , the acceleration of the block relative to the incline is
View SolutionA car of mass m starts from rest and acquires a velocity along east `upsilon = upsilonhati (upsilon gt 0)` in two seconds Assuming the car moves with unifrom acceleration the force exerted on the car is .
View SolutionA cricket ball of mass 150 g has an intial velocity u = `(3 hati + 4 hatj)ms^(-1)` and a final velocity `v = -(3hati + 4 hatj) ms^(-1)` , after being hit. The change in momentum (final momentum - initial momentum ) is (in `Kg ms^(1)`)
View SolutionIn the pervious question (6), the magnitude of the momentum transferred during the hit is
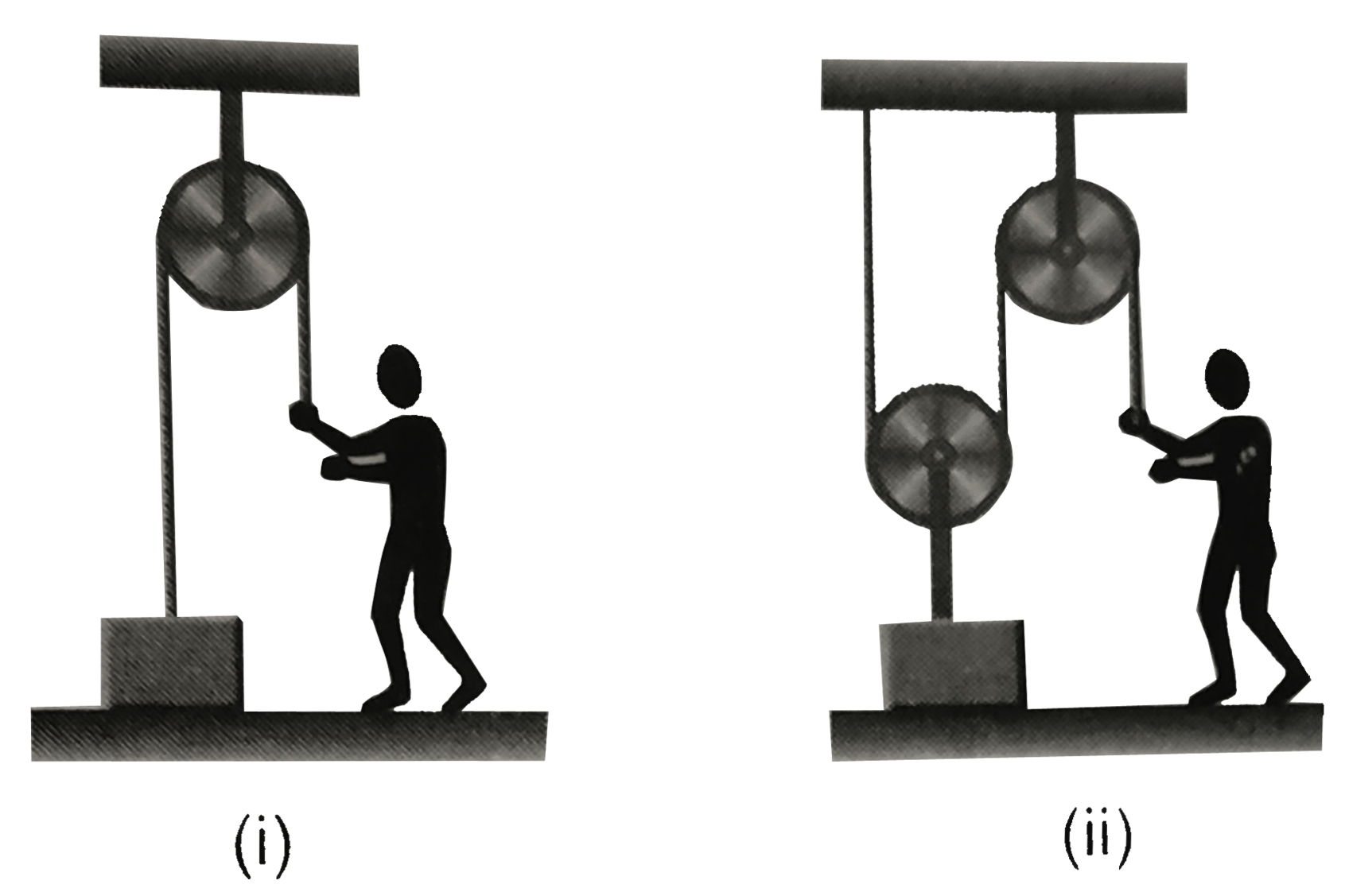
View SolutionIn the figure show , a person wants to raise a block lying on the ground to a height `h` . In which case he has to exert more force. Assume pulleys and strings are light .
View SolutionA body of mass 2kg travels according to the law x(t) = `pt + qt^(2) + rt^(3)` where , q = `4 ms^(-2)` , p = `3 ms^(-1)` and `r = 5 ms^(-3)`. The force acting on the body at t = 2s is
View SolutionA body with mass 5 kg is acted upon by a force `vec(F) = (- 3 hat (i) + 4 hat (j)) N`. If its initial velocity at t =0 is `vec(v) = 6 hat(i) - 12 hat (j) ms^(-1)`, the time at which it will just have a velocity along the y-axis is :
View SolutionA block of mass m is placed on a smooth inclined plane of inclination `theta` with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block has been placed on an inclined plane . The slope angle of `theta` of the plane is such that the block slides down the plane at a constant speed . The coefficient of kinetic friction is equal to :
View SolutionA 5000 kg rocket is set for vertical firing. The exhaust speed is 800 `m//s`. To give an initial upward acceleration of 20 `m//s^(2)`, the amount of gas ejected per second to supply the needed thrust will be (Take `g = 10 m//s^(2)`)
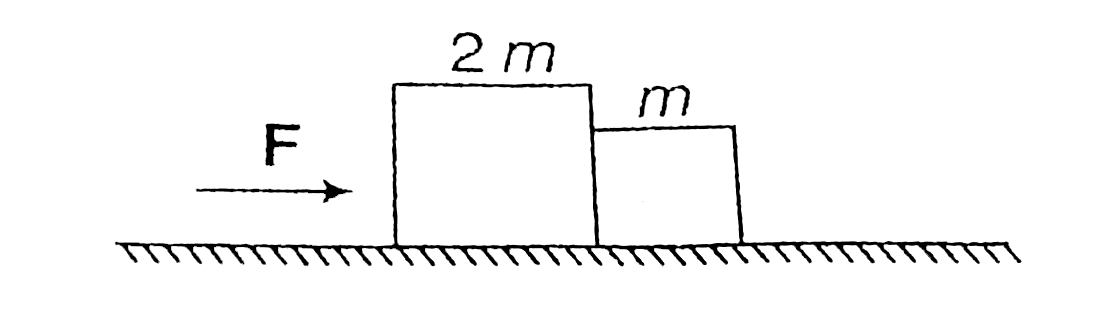
View SolutionTwo blocks are in contact on a frictionless table. One has mass m and the other 2m. A force F is applied on 2m as shown in the figure. Now the same force F is applied from the right on m. In the two cases the ratio of force of contact between the two blocks will be
View SolutionA 4 kg block A is placed on the top of 8 kg block B which rests on a smooth table.

A just slips on B when a force of 12 N is applied on A. Then the maximum horizontal force F applied on B to make both A and B move together, is
View SolutionFind the value of friction forces between the blocks A and B and between B and ground. ( Take , `g=10 ms^(-2)`)

View SolutionA block of mass 5 kg is kept on a horizontal floor having coefficient of friction 0.09. Two mutually perpendicular horizontal forces of 3 N and 4 N this block. The accelation of the block is ( take, `g=10 ms^(-2)`)
View SolutionTwo masses `A` and `B` of `10 kg` and `5 kg`, respectively , are connected with a string passing over a frictionless pulley fixed at the corner of a table as shown. The coefficient of static friction between `A` and the table is `0.2`. The minimum mass `C` that should be placed on `A` to prevent it from moving is equal to

View SolutionTwo blocks of masses 2m and m are in equilibrium a shown in the figure. Now the string between the blocks is suddenly broken. The accelarations of the blocks A and B respectively, at that instant are

View SolutionIn the figure, pulleys are smooth and strings are massless, `m_(1)`=1 kg and `m_(2)=(1)/(3)`kg. To keep `m_(3)` at rest, mass `m_(3)` should be
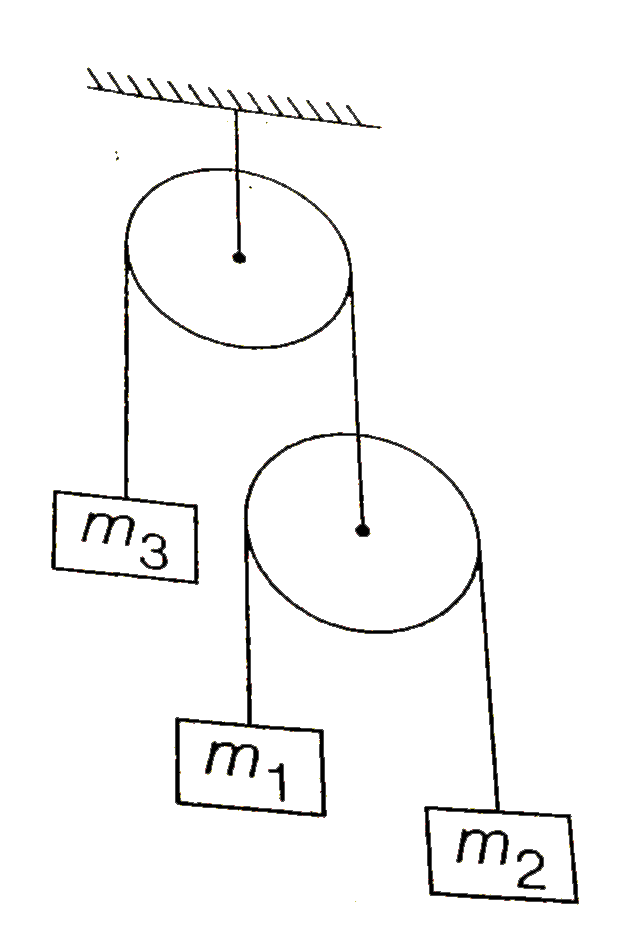
View SolutionIf the coefficient of friction between `A` and `B` is `mu`, the maximum acceleration of the wedge `A` for which `B` will remain at rest with respect to the wedge is

View SolutionA block of mass 1 kg is at rest elative to a smooth wedge moving leftwards with constant aasseleraton`a=5m//s^(2)` Let N be the noemal reaction between block and the wedge .Then `(g=10m//s^(2)`)

View SolutionA block of mass m is kept on an inclined plane of a lift moving down with acceleration of `2 ms^(-1)`.What should be the coefficient of friction to let the block move down with constant velocity relative to lift.
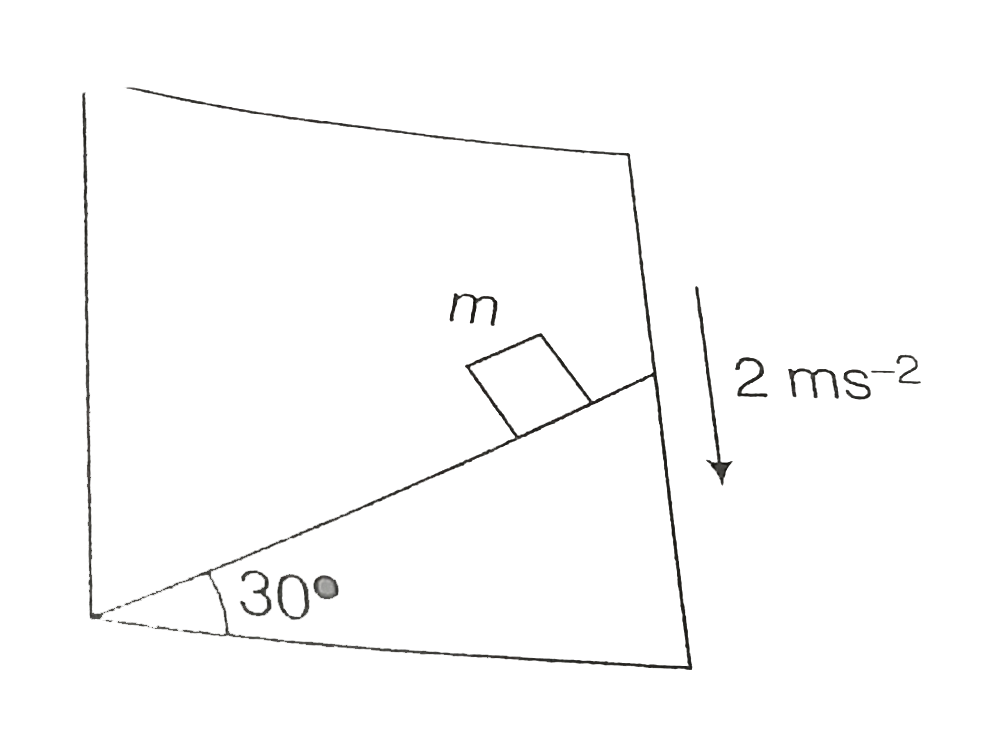
View SolutionTwo blocks of mass 5 kg and 3 kg are attached to the ends of a string passing over a smooth pulley fixed to the ceiling of an elevator. A man inside the elevator accelerated upwards, finds the acceleration of the blocks to be `(9)/(32)g`. The acceleration of the elevator is
View SolutionA balloon of weight w is falling vertically downward with a constant acceleration `a(gt g)`. The magnitude of the air resistance is
View SolutionA smooth inclined plane of length L, having an inclination `theta` with horizontal is inside a lift which is moving down with retardation a. The time taken by a block to slide down the inclined plane from rest will be
View SolutionA body of mass M at rest explodes into three pieces, two of which of mass M//4 each are thrown off in perpendicular directions with velocities of `3//s` and `4m//s` respectively. The third piece will be thrown off with a velocity of
View SolutionA wooden box of mass `8kg` slides down an inclined plane of inclination `30^(@)` to the horizontal with a constant acceleration of `0.4ms^(-2)` What is the force of friction between the box and inclined plane ? `(g = 10m//s^(2))` .
View SolutionA particle is projected along the line of greatest slope up a rough plane inclined at an angle of `45^(@)` with the horizontal. If the coefficient of friction is `1//2` . Their retardation is:
View SolutionA mass of `3kg` descending vertically downwards supports a mass of `2kg` by means of a light string passing over a pulley At the end of `5s` the string breaks How much high from now the `2kg` mass will go `(g = 9.8m//^(2))`.
View SolutionThe rear side of a truck is open and a box of mass 20kg is placed on the truck 4 meters away from the open end coefficient of friction between truck and block is 0.15 the truck starts from rest with an acceleration of `2m//sec^(2)`on a straight road The box will fall off the truck when truck is at a distance from the starting point equal to`(g=10m//s^(2))`
View SolutionTwo blocks of masses `m =5kg and M =10kg` are connected by a string passing over a pulley `B` as shown. Another string connect the center of pulley `B` to the floor and passes over another pulley `A` as shown. An upwards force `F` is applied at the center of pulley `A`. Both the pulleys are massless.
Find the acceleration of block `m` and `M`, if `F` is
(a) `100N`
`300N`
`500N(Take g = 10m//s^(2))`

View SolutionA man of mass `m` stands on a platform of equal mass `m` and pulls himself by two ropes passing over pulleys as shown in figure. If he pulls each rope with a force equal to half his weight ,his upwards acceleration would be

View SolutionBlock of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizontal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are
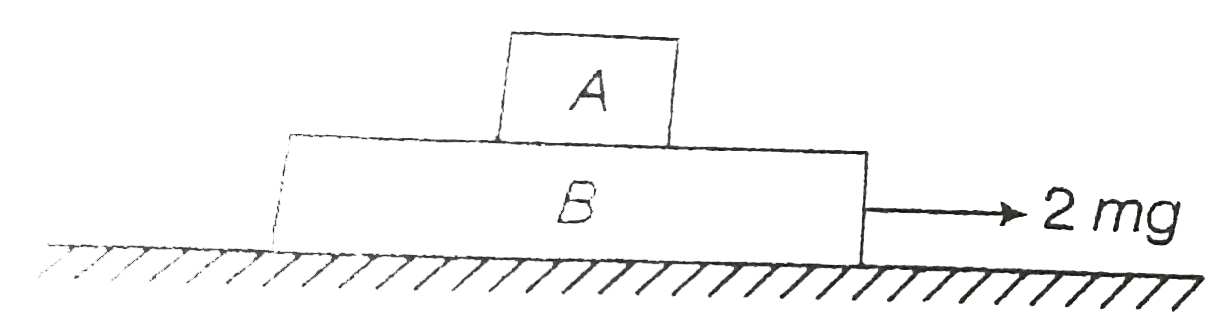
View SolutionA ball is dropped on the floor from a height of 10m. It rebounds to a height of 2.5 m if the ball is in contact with floor for 0.01 s then the average acceleration during contact is nearly
View SolutionA chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
View SolutionA 40 N block is supported by two ropes. One rope is horizontal and other makes an angle of `30^(@)` with the ceiling. The tension in the rope attached to the ceiling is approximately
View SolutionConsider the shown arrangement. Assume all surfaces to be smooth. If N represents magnitudes of normal reaction between block and wedge, then acceleration of M along horizontal is equla to

View SolutionIn the above problem normal reaction between ground and wedge will have magnitude equla to
View SolutionStarting from rest a body slides down a `45^(@)` inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of the body and the inclined plane is :
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA block of mass m is given an initial downward velocity `v_(0)` and left on inclined place ( coefficient of friction =0.6). The block will
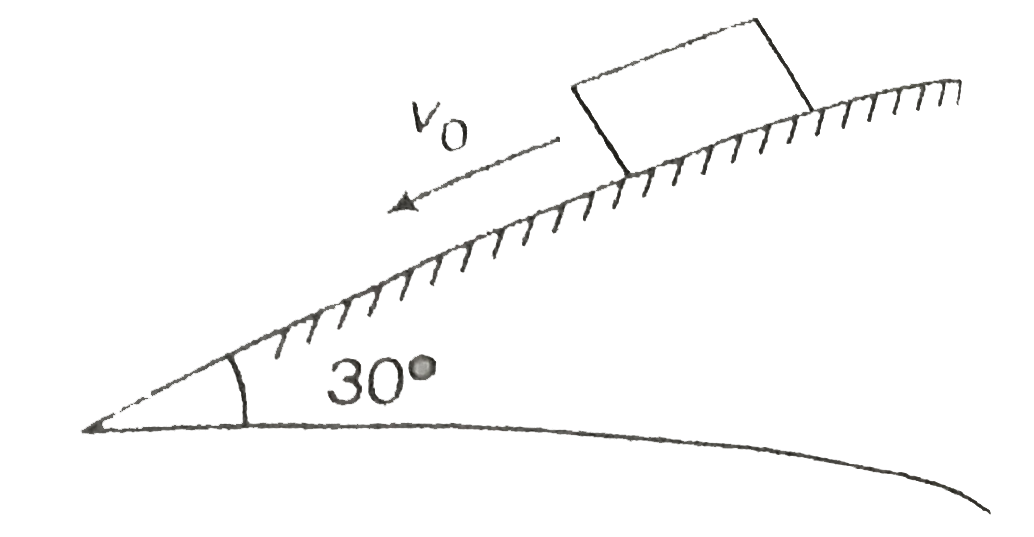
View SolutionA block of mass m slides down an inclined plane which makes an angle `theta` with the horizontal. The coefficient of friction between the block and the plane is `mu`. The force exerted by the block on the plane is
View SolutionThe upper half of an inclined plane with inclination `phi` is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View SolutionPushing force making an angle `theta` to the horizontal is applied on a block of weight W placed on a horizontal table . If the angle of friction is `phi` , magnitude of force required to move the body is equal to :
View SolutionIn the arrangement shown in figure, there is a friction force between the blocks of masses m and 2m. The mass of the suspended block is m. The block of mass m is stationary with respect to block of mass 2m. The minimum value of coefficient of friction between m and 2m is
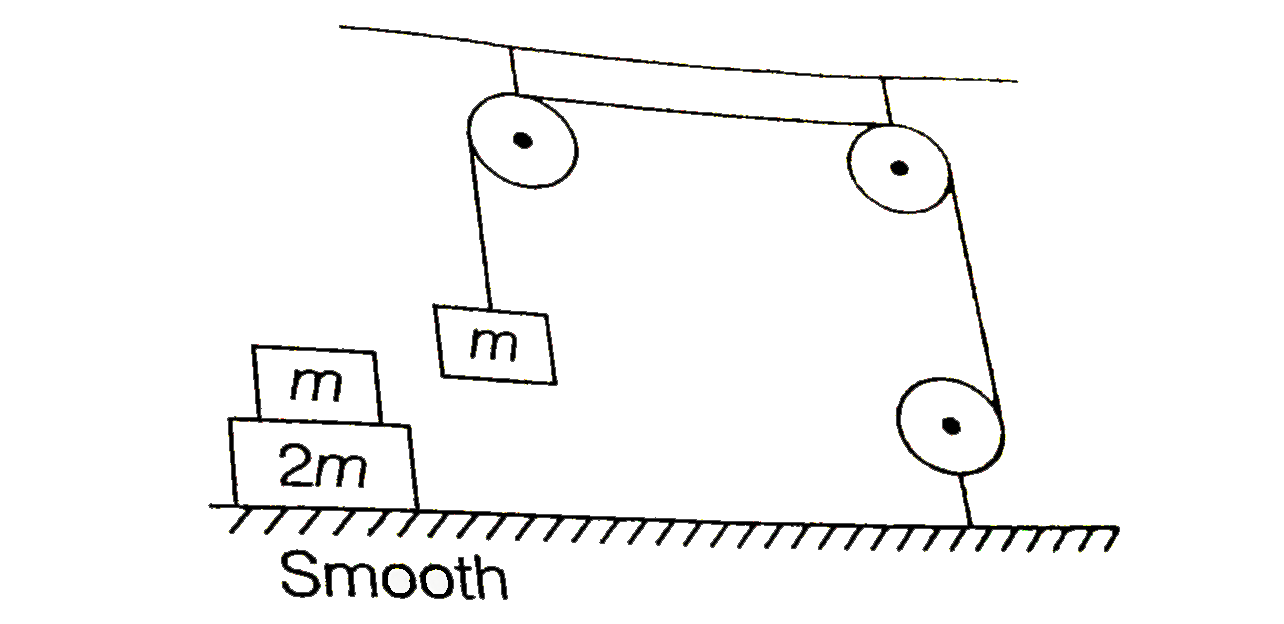
View SolutionTwo masses `m` and `M` are attached with strings as shown. For the system to be in equilibrium we have.

View SolutionA man has fallen into a ditch of width d and two of his friends are slowly pulling him out using a light rope and two fixed pulleys as shown in figure. Indicate the correct statements : (assume both the friends apply equal forces of equal magnitude)

View SolutionTwo beads `A` and `B` move along a semicircular wire frame as shown in figure. The beads are connected by an inelastic string which always remains tight . At an instant the speed of `A` is `u,/_BAC = 45^(@) and BOC = 75^(@)`,where `O` is the centre of the semicircular arc. The speed of bead `B` at that instant is
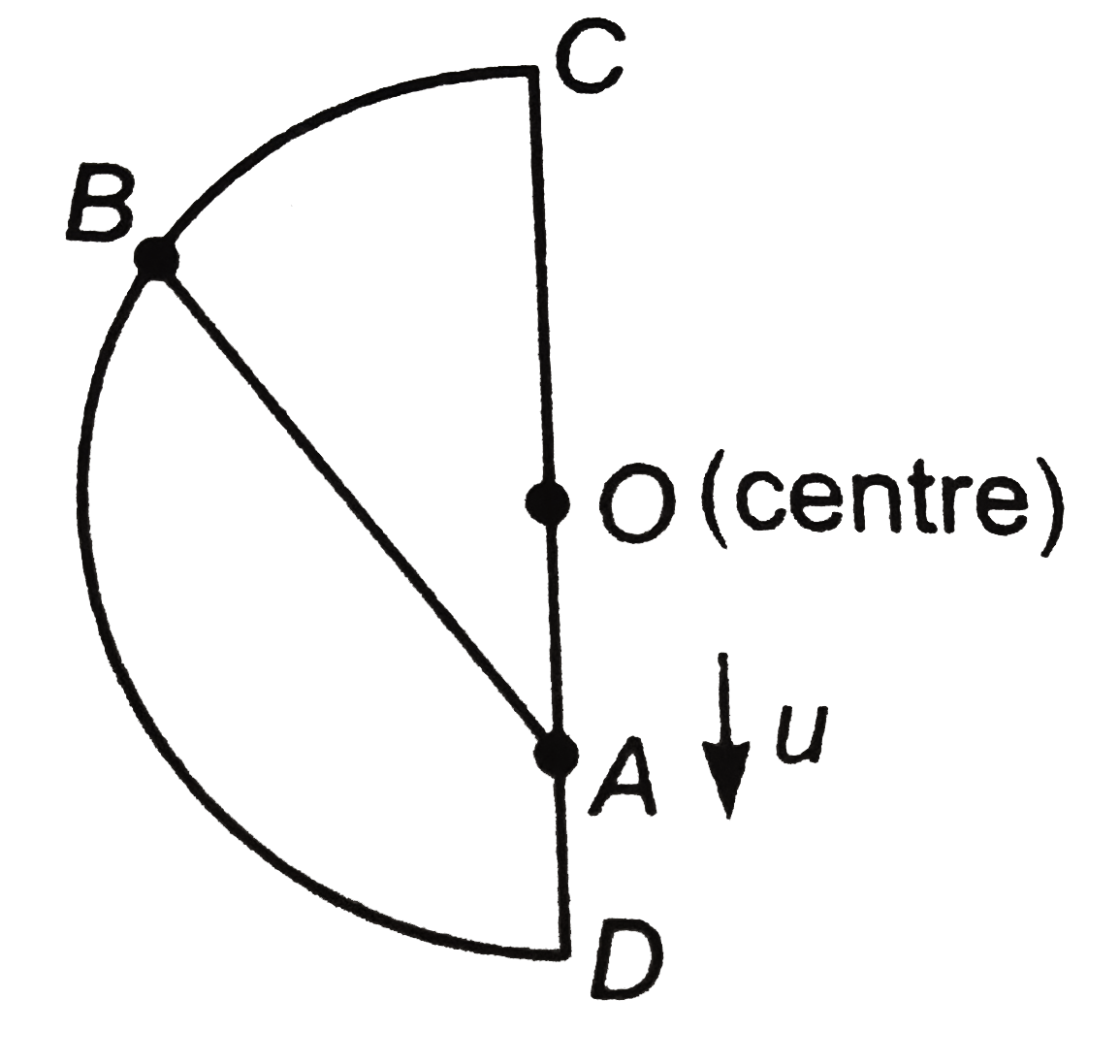
View SolutionTwo blocks of masses m and 2 m are placed one over the other as shown in figure.The coefficient of friction between m and 2m is `mu` and between 2m and ground is `(mu)/(3)`. If a horizontal force F is applied on upper block and T is tension developed in string, then choose the incorrect alternative.
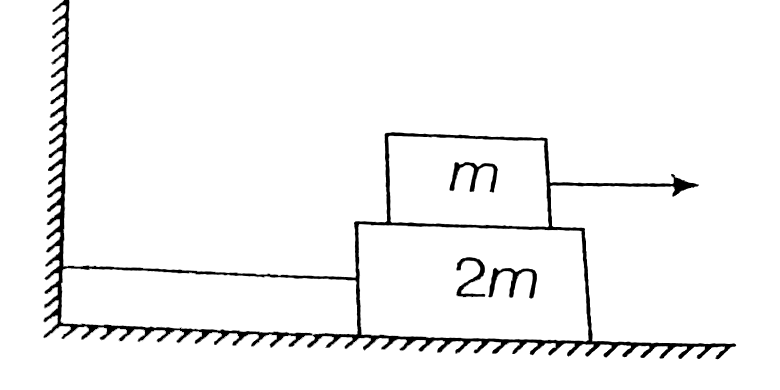
View SolutionIf a body looses half of its velocity on penetrating 3 cm in a wooden block, then how much will it penetrate more before coming to rest?
View SolutionA ball is moving towards the wall as shown in diagram then momentum is conserved
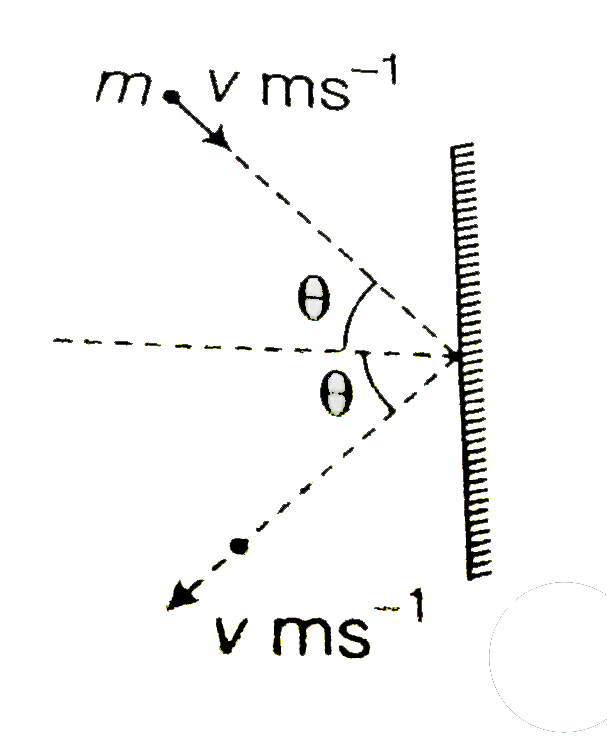
View SolutionTwo weights `w_(1)` and `w_(2)` are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up at an acceleration g , the tension in the string will be
View SolutionA dynamometer D is attached to two bodies of masses M=6 kg and m=4 kg. Force F=20 N and f=10N are applied to the masses as shown. The dynometer reads

View SolutionTwo blocks are connected over a massless pulley as shown in figure. The mass of block A is 10 kg and the coefficient of kinetic friction is 0.2 Block A sliders down the incline at constant speed. The mass of block B in kg is

View SolutionA block of mass 5 kg resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass 5 kg. The coefficient of kinetic friction between the block and surface is 0.5. Tension in the cord is (take, `g=9.8ms^(-2)`)

View SolutionA block of mass 3kg is at rest on a rough inclined plan as shown in the Figure. The magnitude of net force exerted by the surface on the block will be

View SolutionTwo block of masses M and m are connected to each other by a massless string and spring of force constant k as shown in the figure. The spring passes over a frictionless pulley connected rigidly to the egde of a stationary block A. The coefficient of friction between block M and plane horizontal surface of A is `mu`. The block M slides over the horizontal top surface of A and block m slides vertically downward with the same speed. The mass M is equal to

View SolutionAn insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle `alpha` with the vertical, the maximum possible value of `alpha` is given by
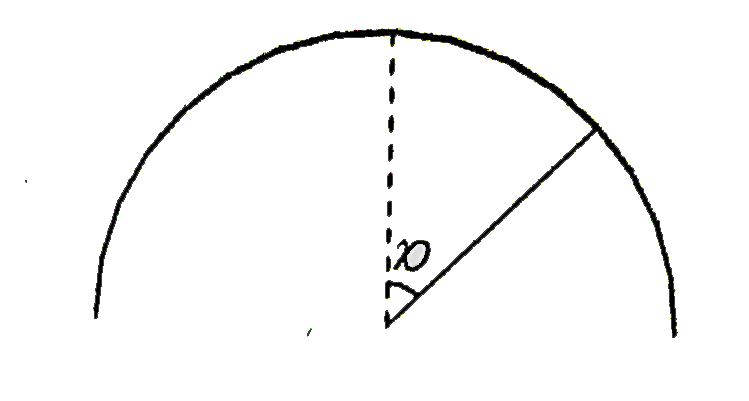
View SolutionA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle `theta` to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View SolutionIn the figure shown if coefficient of friction is `mu`, then `m_(2)` will start moving upwards if
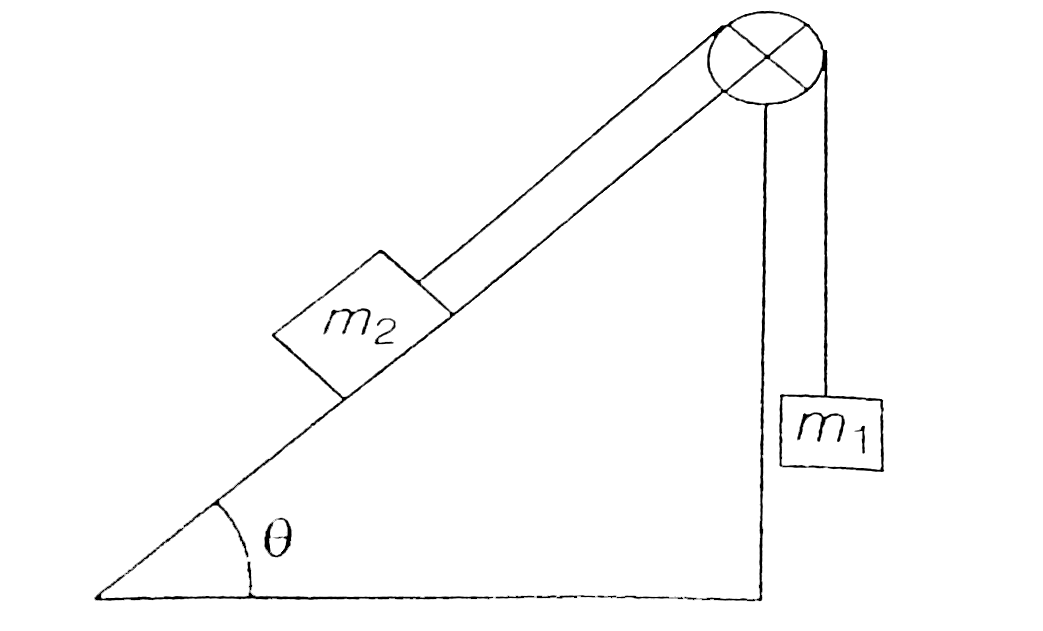
View SolutionA block of mass M rests on a rough horizontal surface as shown. Coefficient of friction between the block and the surface is `mu`. A force F=mg acting at angle `theta` with the vertical side of the block pulls it. In which of the following cases the block can be pulled along the surface?

View SolutionTwo blocks A and B each of mass m are placed on a smooth horizontal surface. Two horizontal force F and 2F are applied on blocks A and B, respectively, as shown in fig. Block A does not slide on block B. Then then the normal reaction acting between the two blocks is (assume no friction between the blocks)
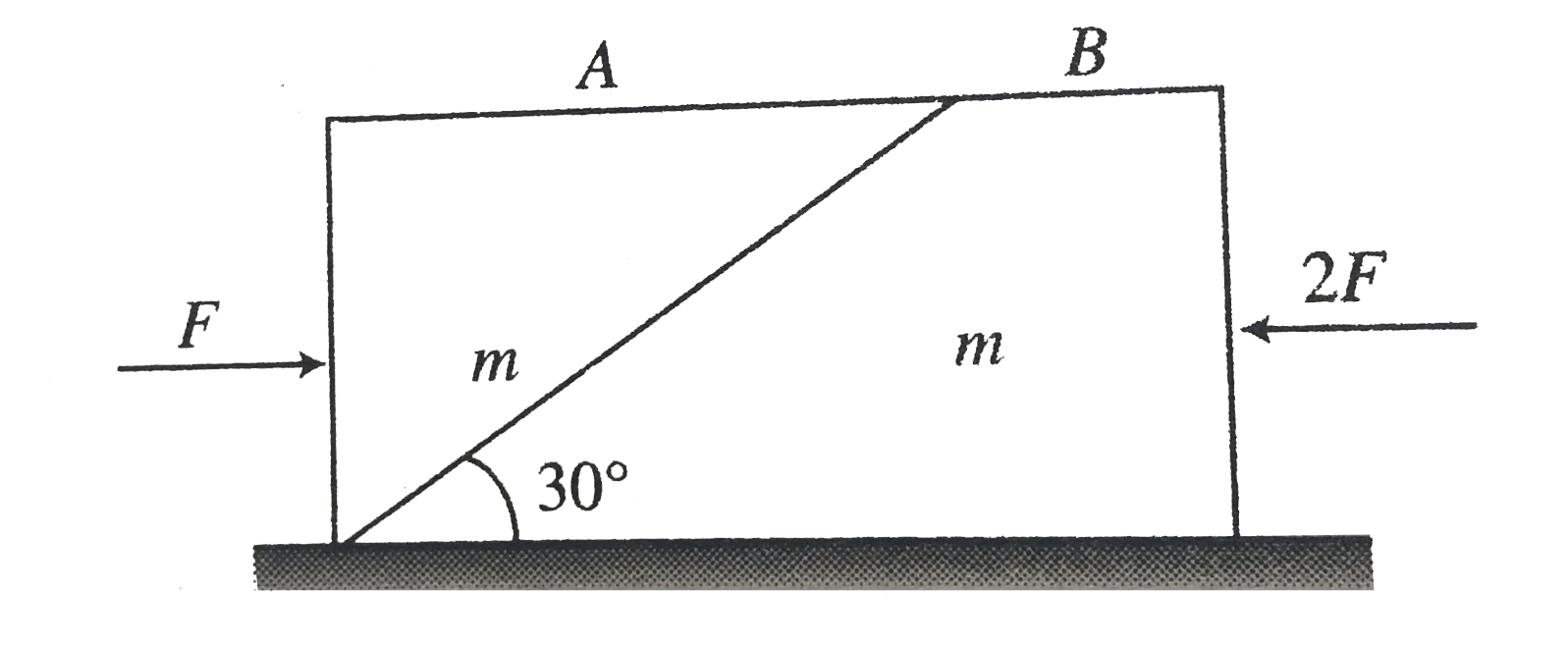
View SolutionA wedge of mass 2m and a cube of mass m are shown in figure. Between cube and wedge, there is no friction. The minimum coefficient of friction between wedge and ground so that wedge does not move is:

View SolutionIf the coefficient of friction between all surface figure is `0.4` then find the minimum force `F` to have equilibrium of the system.

View SolutionBlock B moves to the right with a constant velocity `v_(0)`. The velocity of body A relative to B is
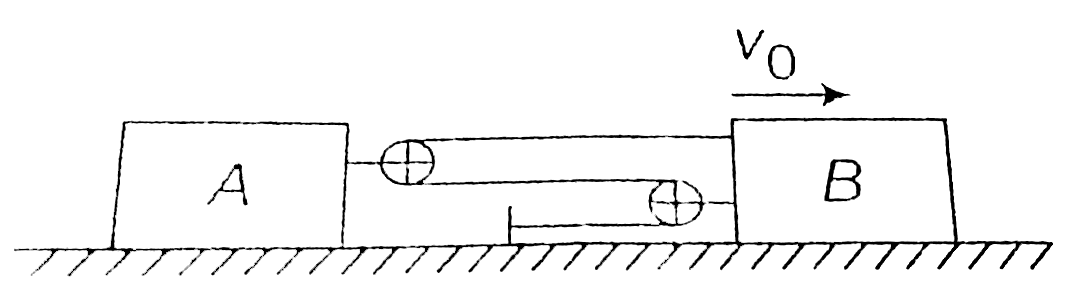
View SolutionA sphere of mass m, is held between two smooth inclined walls. For `sin37^(@)=3//5`, the normal reactions of the wall (2) is equal to

View SolutionA pendulum of mass m hangs from a support fixed to a trolley. The direction of the string when the trolley rolls up a plane of inclination `alpha` with acceleration `a_(0)` is

View SolutionA uniform rope of length L meters is lying over a table. If the coefficient of friction be `mu`, then the maximum length `L_(1)` of the part of the rope which can overhang the edge without sliding is
View Solution
Chapter exercises (A) Taking it together questions and complete solutions for chapter LAWS OF MOTION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY NEET Class 11 PHYSICS LAWS OF MOTION
- Chapter exercises (A) Taking it together
- Check point 5.1
- Check point 5.2
- Check point 5.3
- Check point 5.4
- Comprehension
- Exercise 8.1
- Exercise 8.2
- Exercise 8.3
- Exercise 8.4
- Exercise 8.5
- Match the columns
- Medical entrances gallery
- Miscellaneous Examples
- Objective Question
- Single Correct
- Solved Examples
- Subjective Question