Complete Solutions to Example of chapter ROTATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATION |
| DC PANDEY NEET | Example |
| Number Of Questions | 53 |
| Academic Year | 2023-24 |
A ring of diameter 0.4 m and of mass 10 kg is rotating about its geometrical axis at the rate of 35 ratation/second. Find the moment of intertia.
01:03View SolutionThree point masses `m_(1), m_(2)` and `m_(3)` are located at the vertices of an equilateral triangle of side `alpha`. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through `m_(1)?`
02:01View SolutionCalculate moment of inertia w.r.t. rotational axis XX' in following figures.
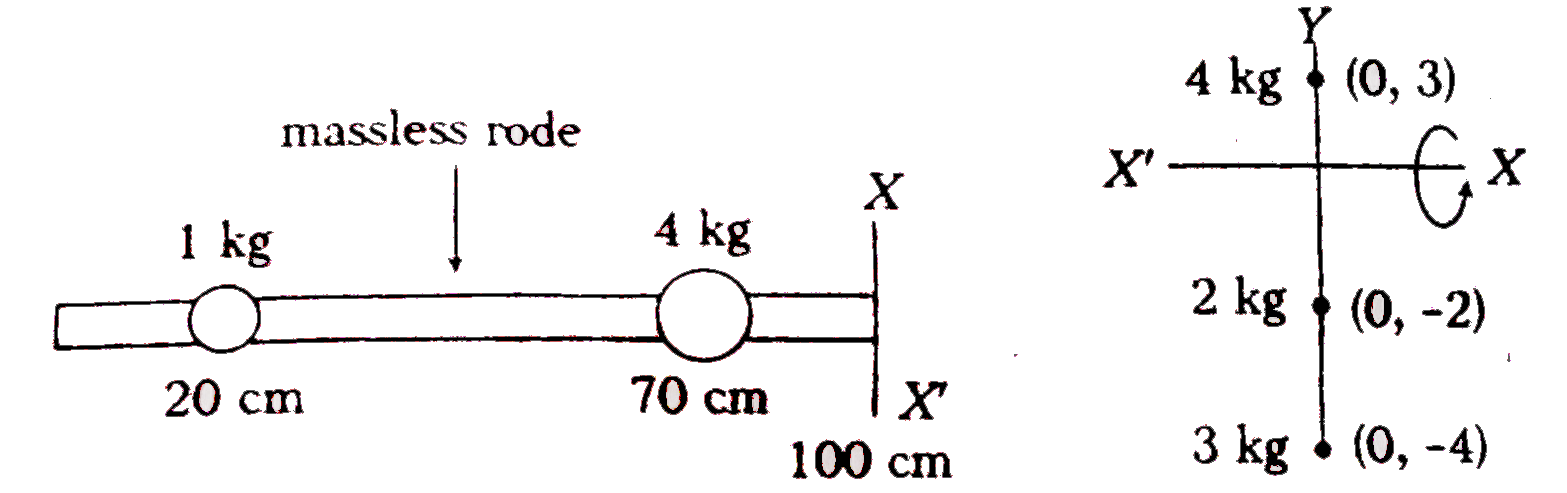 04:14View Solution
04:14View SolutionFind the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
06:31View SolutionA wheel of mass 8 kg has moment of inertia equals to `0.5 "kg-m"^(2)`. Determine its radius of gyration.
01:26View SolutionThe moment of inertia of a solid cylindrer about its axis of ratation is `(MR^(2))/(2)`. What is the value if the radius of gyration of the cylinder about this axis ?
01:15View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
01:49View SolutionThe mass of the cylinder is 25 kg and radius of cylinder is 5 m. Find the moment of inertia of a solid cylinder about a tangent to the cylinder.
02:04View Solution
Find the moment of inertia of a solid sphere of mass `M` and radias `R` about an axis XX shown in figure. Also find radius of gyration about the given axis.02:34View SolutionWhat is the moment of inertia of a
(i) uniform circular ring of mass 2 kg about its 4 m diameter ?
(ii) a thin disc about an axis coinciding with a diameter ?04:05View SolutionCalculate the moment of inertia of a rod of mass 2 kg and length 5 m about an axis perpendicular to it and passing through one of its ends.
02:48View SolutionTwo masses `m_(1) and m_(2)` are placed at a distance r from each other. Find out the moment of inertia of system about an axis passing through their centre of mass.
04:27View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.
 01:38View Solution
01:38View SolutionConsider a uniform rod of mass m and length 2l with two particles of mass `m` each at its ends. Let AB be a line perpendicular to the length of rod and passig through its centre. Find the moment of inertial of the system about AB.
02:29View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passig through its centre of mass and perpendicular to the plane of the particle.03:36View SolutionTwo thin uniform rods `A` (`M.L`) and `B` (`3M,3L`) are joined as shown. Find the `M.I.` about an axis passing through the center of mass of system of rods and perpendicular to the length.
 05:09View Solution
05:09View SolutionTwo thin uniform rings made of same material and of radii `R` and `4 R` are joined as shown. The mass of smaller ring is `m`. Find the `M.I.` about an axis passing through the center of mass of system of rings and perpendicular to the plane.
07:00View SolutionFind the torque of a force `vecF=(2hat(i) +hat(j)-3hat(k))N` about a point O. The position vector of point of application of force about O is `vecr = (2 hat(i) + 3 hat(j) - hat(k))m`.
01:25View SolutionA force of `-4Fhat(K)` acts O, the origin of the coordinate system. The torque about the point `(1,-1)` is
02:24View SolutionThe body in figure shown is pivoted at O and two forces acts on it as shown
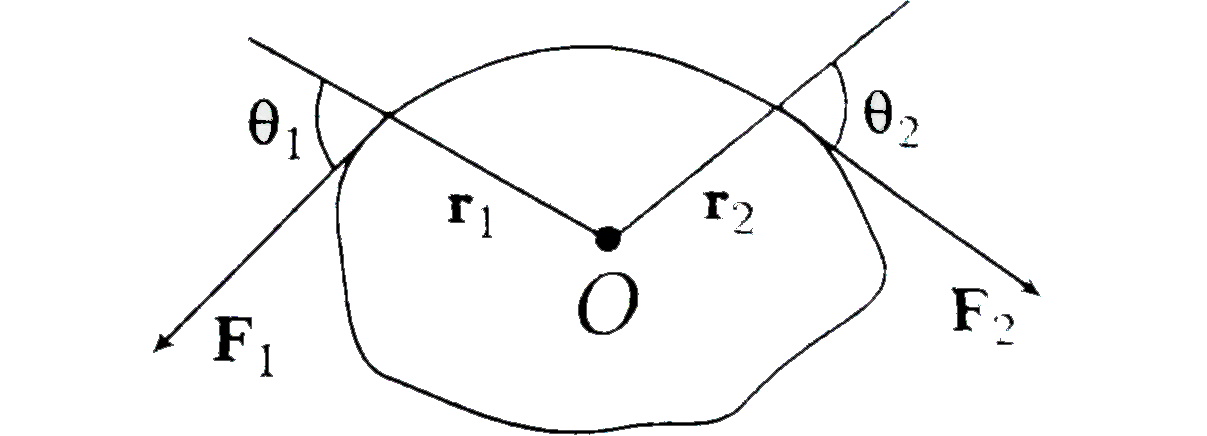
(i) Find an expression of the net torque on the body about the pivot
(ii) If `r_(1)=1.30 m,r_(2)=2.15 m,F_(1)=4.20N,F_(2)=4.90 N,theta_(1)=75^(@)` and `theta_(2) = 60^(@)`, what is the net torque about the pivot ?04:13View SolutionA small ball of mass 1.0 kg is attached to one end of a 1.0 m long massless string and te other end of the string is hung from a point `O`. When the resulting pendulum is making `30^(@)C` from the vertical, what is the magnitude of net torque about the point of suspension? [Take `g=10m//s^(2)`]
03:02View SolutionA solid flywheel of 20 kg mass and 120 mm radius revolves at `600 "revmin"^(-1)`. With what force must a brake lining be pressed against it for the flywheel to stop in 3s, if the coefficient of friction is 0.1 ?
05:02View SolutionTo maintain a rotor at a uniform angular speed of 100 `rads^(-1)` an engine needs to transmit a torque of 200 Nm. What is the power required by engine ? Assume 100 % efficiency of engine.
02:02View SolutionThe power output of an antomobile engine is advertised to be 200 at 6000 rpm. What is the corresponding torque ?
01:11View SolutionA flywheel of moment of inertia `10kg m^(2)` is rotating at `50 rad//s`. It must be brought to stop in `10 s`.
(a) How much work must be done to stop it?
(b) What is the required average power?02:54View SolutionA car of mass 300 kg is travelling on a circular track of radius 100 m with a constant speed of 60 m/s
Calculate the angular momentum ?01:15View SolutionA particle of mass `m` is moving along the line `y=b,z=0` with constnat speed `v`. State whether the angular momentum of particle about origin is increasing. Decreasing or constant.
02:42View SolutionA particle of mass m is projected with a velocity `mu` at an angle of `theta` with horizontal.The angular momentum of the particle about the highest point of its trajectory is equal to :
01:30View SolutionFind the components along the `x,y,z` axes of the angular momentum `overset rarr(L)` of a particle, whose position vector is `overset rarr(r )` with components `x,y,z` and momentum is `overset rarr(p)` with components `p_(x), p_(y) and p_(z)`. Show that if the particle moves only in the `x-y` plane, the angular momentum has only a z-component.
03:42View SolutionA `40 kg` flywheel in the from of a uniform circular disc of `1 m` radius is making `120` rpm. Calculate the angular momentum.
02:45View SolutionA torque of 10 Nm is applied on a wheel having angular momentum of `2 kg m^(2)s^(-1)`, calculate the angular momentum of the wheel after 4 seconds.
01:04View SolutionThe diameter of a solid disc is 0.5 m and its mass is 16 kg. What torque will increase its angular velocity from zero to 120 ratations/minute in 8 seconds.
03:34View SolutionA solid ball of radius 0.2 m and mass 1 kg is given an instantaneous impulse of 50 N-s at point P as shown. Find the number of rotations made by the ball about its diameter before hitting the ground. The ball is kept on smooth surface intially
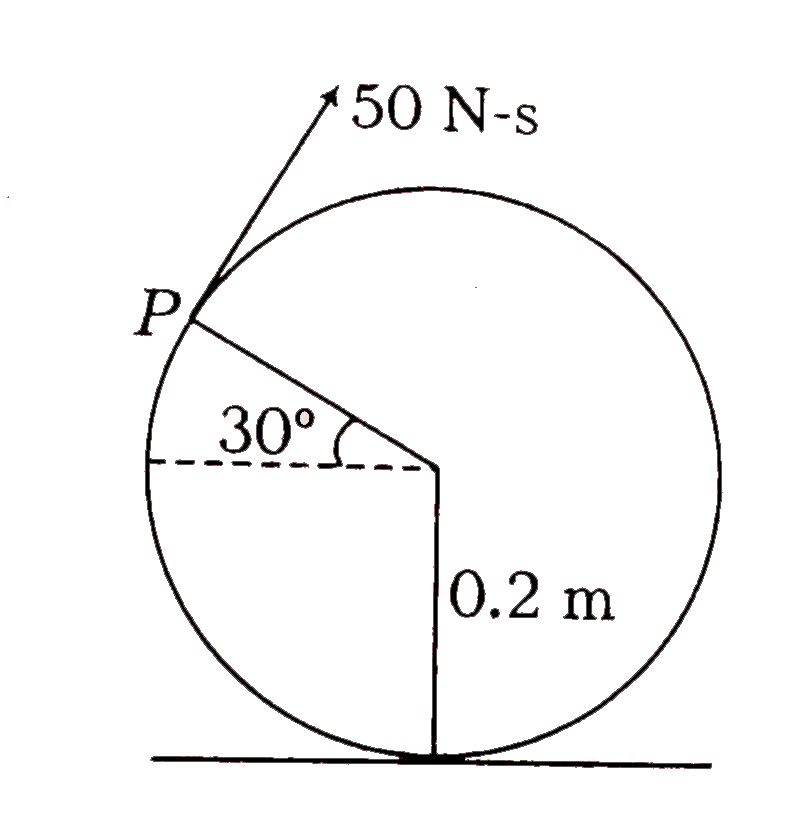 08:09View Solution
08:09View SolutionThe maximum and minimum distances of a cornet form Sun are `1.4 xx 10^(12) m and 7 xx 10^(10) m`. If velocity nearest to Sun is `6 xx 10^(4) ms^(-1)`, what is velocity if cornet when it is farthest from the Sun ?
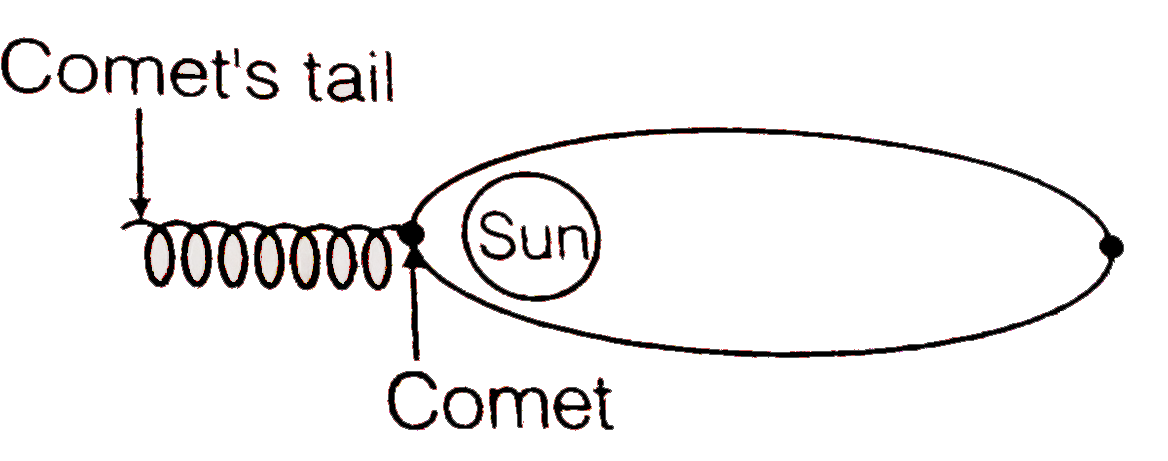 01:58View Solution
01:58View SolutionA wheel of moment of inertial I and radius R is rotating about its axis at an angular speed `omega`. It picks up a stationary particle of mass `m` at its edge. Find the new angular speed of the wheel.
02:25View SolutionIf the radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
03:38View SolutionA wheel is rotating at a speed of 1000 rpm and its KE is `10^(6) J`. What is moment of inertia of the wheel about its axis of rotation ?
02:36View SolutionA flywheel of mass 0.2 kg and radius 10 cm is rotating with `5//pi "rev/s"` about an axis perpendicular to its plane passing through its centre. Calculate angular momentum and kinetic energy of flywheel.
02:54View SolutionAn energy of `484 J` is spent in increasing the speed of a flywheel from 60 rpm to 360 rpm. Calculate moment of inertia of flywheel.
03:16View SolutionIf the rotational kinetic energy of a body is increased by 300 %, then determine percentage increase in its angular momentum.
03:57View SolutionA thin meter scale is kept vertical by placing its one end on floor, keeping the end in contact stationary, it is allowed to fall. Calculate the velocity of its upper end when it hit the floor.
01:32View SolutionA disc of mass 5 kg and radius 50 cm rolls on the ground at the rate of `10 ms^(-1)`. Calculate the K.E. of the disc.
01:05View SolutionA hollow sphere of mass `M` and radius `R` lies on a rough horizontal plane when a particle of mass `m` traveling with speed `v` collides and sticks with it. If line of motion of the particle is at height `h` above the center of sphere, find `h` if the body rolls without slipping after collision (`m lt lt M`).
09:05View SolutionA solid cylinder of mass m and radius r starts rolling down an inclined plane of inclination `theta`. Friction is enough to prevent slipping. Find the speed of its centre of mass when its centre of mass has fallen a height `h`.
03:38View SolutionA disc of radius R start at time `t=0` moving along the positive X-axis with linear speed b and angular speed `omega`. Find the x and y-coordinates of the bottommost point at any time t.
 02:51View Solution
02:51View SolutionA horizontal force `F` acts on the sphere at its centre as shown. Coefficient of friction between ground and sphere is `mu`. What is maximum value of `F` for which there is no slipping?
06:11View Solution
A tangential force `F` acts at the top of a thin spherical shell of mass `m` and radius `R`. Find the acceleration of the shell if it rolls without slipping.05:58View SolutionA sphere of mass m attached to a spring on incline plane as shown in figure is held in unstretched position of spring. Suddenly sphere is left free what is the maximum extension of spring if friction allows only rolling of sphere about horizontal diametre ?
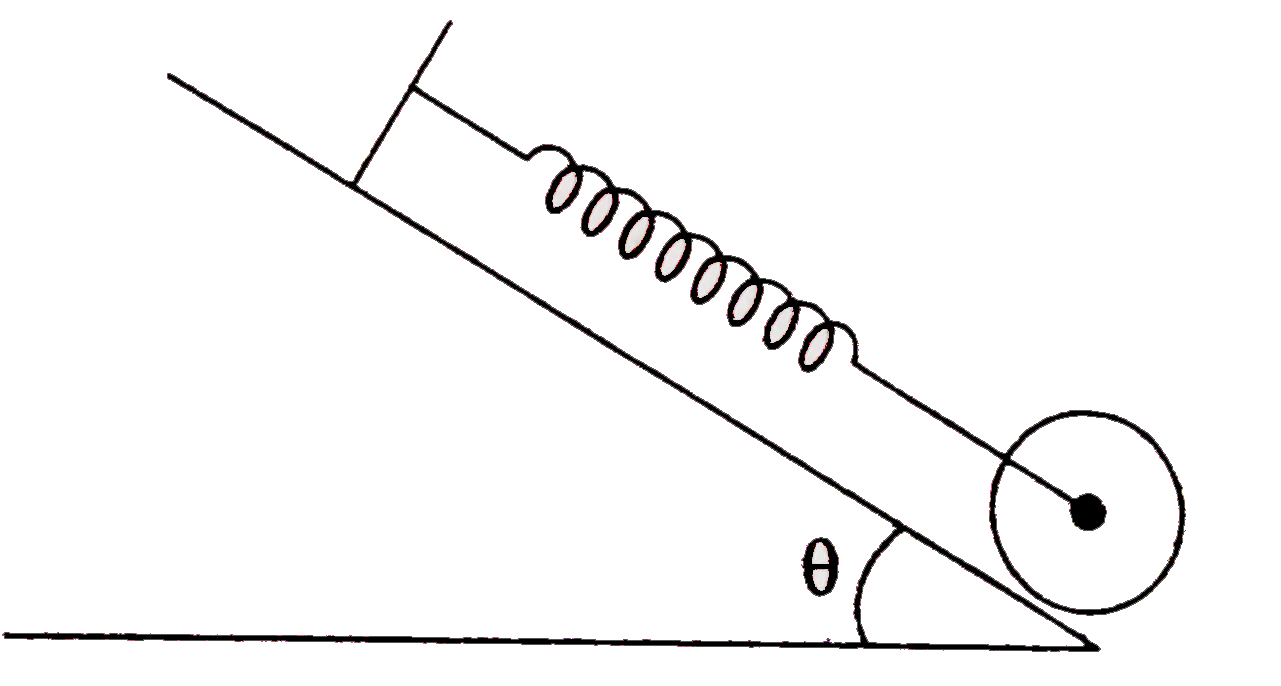 01:33View Solution
01:33View SolutionCalculate the kinetic energy of rolling ring of mass 0.2 kg about an axis passing through its centre of mass and perpendicular to it, if centre of mass is moving with a velocity of 3 m/s.
01:42View SolutionA solid sphere is rolling down an inclined plane without slipping of height 20 m. Calculate the maximum velocity with which it will reach the bottom of the plane `(g = 10 m//s^(2))`
02:15View SolutionA solid disk is rolling without slipping on a level surface at a constant speed of `2.00m//s`. How far can it roll up a `30^(@)` ramp before it stops? (take `g=9.8m//s^(2))`
05:53View SolutionWhen a body is under pure rolling, the fraction of its total kinetic energy which is the purely rotational is 2/5. Identify the body.
03:34View SolutionA uniform sphere of mass `m` and radius `R` rolls without slipping down an inclined plane set at an angle `theta` to the horizontal. Find
(`a`) the friction coefficient at which slipping is absent,
(`b`) the kinetic energy of the sphere `t` seconds after the beginning of motion.17:08View Solution
Example questions and complete solutions for chapter ROTATION of DC PANDEY PHYSICS (HINGLISH) of Class 11
