Complete Solutions to (A) Chapter Exercises of chapter ROTATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATION |
| DC PANDEY NEET | (A) Chapter Exercises |
| Number Of Questions | 83 |
| Academic Year | 2023-24 |
The angular momentum of a system of particles is conserved
01:21View SolutionIf a person standing on a rotating disc stretches out his hands, the angular speed will
02:27View SolutionWhen a disc rotates with uniform angular velocity, which of the following is not true ?
02:11View SolutionA ring of diameter 0.4 m and of mass 10 kg is rotating about its axis at the rate of 1200 rpm. The angular momentum of the ring is
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed `omega` in a horizontal plane. About a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddently attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA uniform square plate has a small piece `Q` of an irregular shape removed and guled to the centre of the plate leaving a hole behind in figure. The moment of inertia about the z-axis is then,
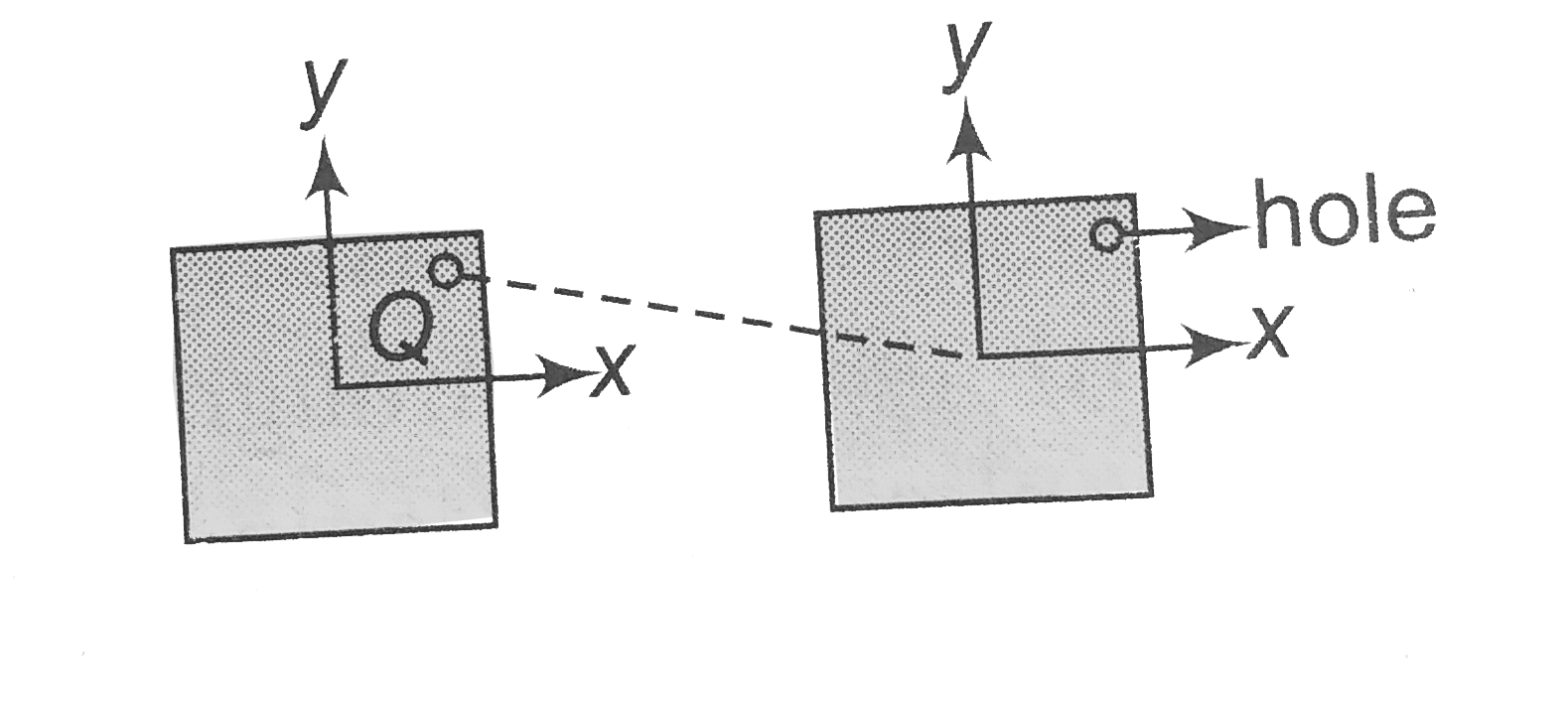 .01:12View Solution
.01:12View SolutionA diver in a swimming pool bends his head before diving, because it
01:16View SolutionA ody is in pure rotation. The linear speed v of a particle, the distance r of the particle from the axis and the angular velocity `omega` of the body are related as `omega=v/r`. Thus
01:42View SolutionThe rotational kinetic energy of a body is E and its moment of inertia is `I`. The angular momentum is
View SolutionA body is under the action of two equal and oppositely directed forces and the body is rotating with constant non-zero angular acceleration. Which of the following cannot be the separation between the lines of action of the forces ?
03:32View SolutionA particle performing uniform circular motion gas angular momentum `L`. If its angular frequency is double and its kinetic energy halved, then the new angular momentum is :
01:36View SolutionMoment of a force of magnitude 10 N acting along positive y-direction at point `(2m,0,0)` about the point `(0,1m,0)` in N-m is
02:13View SolutionThe radius of gyration of a uniform rod of length `L` about an axis passing through its centre of mass is
View SolutionFive particles of mass 2 kg are attached to the rim of a circular disc of radius 0.1 m & negligible mass. Moment of inertia of the system about an axis passing through the centre of the disc & perpendicular to its plane is
04:17View SolutionA particle is moving in a circular orbit with constant speed. Select wrong alternate.
02:13View SolutionIf the equation for the displacement of a particle moving on a circle path is given by, `theta = 2t^(2)+0.5` where, `theta` is in radian and `t` is in second, then the angular velocity of the particle after 2 s is
View SolutionA wheel is a rest. Its angular velocity increases uniformly and becomes `80 rad s^(-1)` after 5 s. The total angular displacement is
View SolutionA rigid body rotates about a fixed axis with variable angular velocity equal to `alpha-beta`, at the time t, where `alpha,beta` are constant. The angle through which it rotates before its stops
View SolutionA wheel is rotating at the rate of `33 "rev min"^(-1)`. If it comes to stop in 20 s. Then, the angular retardation will be
View SolutionA wheel is rotating at 900 rpm about its axis. When power is cut off it comes to rest in 1 min. The angular retardation in `rad s^(-2)` is
View SolutionA wheel is subjected to uniform angular acceleration about its axis. Initially, its angular velocity is zero. In the first `2 sec`, it rotates through an angle `theta_(1)`, in the next `2 sec`, it rotates through an angle `theta_(2)`. The ratio of `theta_(2)//theta_(1)` is
02:05View SolutionThe motor of an engine is rotating about its axis with an angular velocity of 100 rpm. It comes to rest in 15 s after being switched off. Assuming constant angular deceleration, calculate the number of revolution made by it before coming to rest.
02:11View SolutionIf `vec F` is the force acting in a particle having position vector `vec r` and `vec tau` be the torque of this force about the origin, then
01:20View SolutionA particle of mass 5 kg is moving with a uniform speed of `3 sqrt(2) "cm s"^(-1)` in the XY-plane along the line `y = 2 sqrt(5)` cm. The magnitude of its angular momentum about the origin in `"g-cm"^(2) s^(-1)` is
View SolutionA particle of mass `m` is moving in yz-plane with a unifrom velocity `v` with its trajectory running parallel to +ve y-axis and intersecting z-axis at `z = a` Fig. The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is :
 03:31View Solution
03:31View SolutionA particle of mass `m=5` units is moving with a uniform speed `v = 3 sqrt(2)` units in the XY-plane along the `y=x+4`. The magnitude of the angular momentum about origin is
05:07View SolutionA particle of mass `2 mg` located at the position `(hat i+ hat k) m` has a velocity `2(+ hat i- hat j + hat k) m//s`. Its angular momentum about `z-`axis in `kg-m^(2)//s` is :
02:12View SolutionA particle of mass m is projected with velocity v moving at an angle of `45^(@)` with horizontal. The magnitude of angular momentum of projectile about point of projection when particle is at maximum height, is
04:27View SolutionA sphere of mass `M` rolls without slipping on rough surface with centre of mass has constant speed `v_0`. If mass of the sphere is `m` and its radius be R`, then the angular momentum of the sphere about the point of contact is.
02:39View SolutionA constant torque of `1000 N-m` turns a wheel of moment of inertia `200 kg-m^2` about an axis through its centre. Its angular velocity after `3` seconds is.
01:28View SolutionA Merry -go-round, made of a ring-like platform of radius `R and mass M`, is revolving with angular speed `omega`. A person of mass `M` is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as see from the round). The speed of the round after wards is
02:38View SolutionA flywheel having a radius of gyration of 2m and mass 10 kg rotates at an angular speed of `5 rad s^(-1)` about an axis perpendicular to it through its centre. The kinetic energy of rotation is
View SolutionA flywheel is in the form of a uniform circular disc of radius `1 m` and mass `2 kg`. The work which must be done on it to increase its frequency of rotation from `5` to `10 rev//s` is approximately
03:47View SolutionA rod is placed along the line,`y=2x` with its centre at origin. The moment of inertia of the rod is maximum about.
03:51View SolutionThe ratio of the radii of gyration of a circular disc and a circular ring of the same radii about a tangential axis perpendicular to plane of disc or ring is
View SolutionLet `I_(A) and I_(B)` be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
View SolutionThe ratio of the radii of gyration of a hollow sphere and a solid sphere of the same radii about a
View SolutionA square lamina is as shown in figure. The moment of inertia of the frame about the three axes as shown in figure `I_(1),I_(2) and I_(3)` respectively. Select the correct alternative.
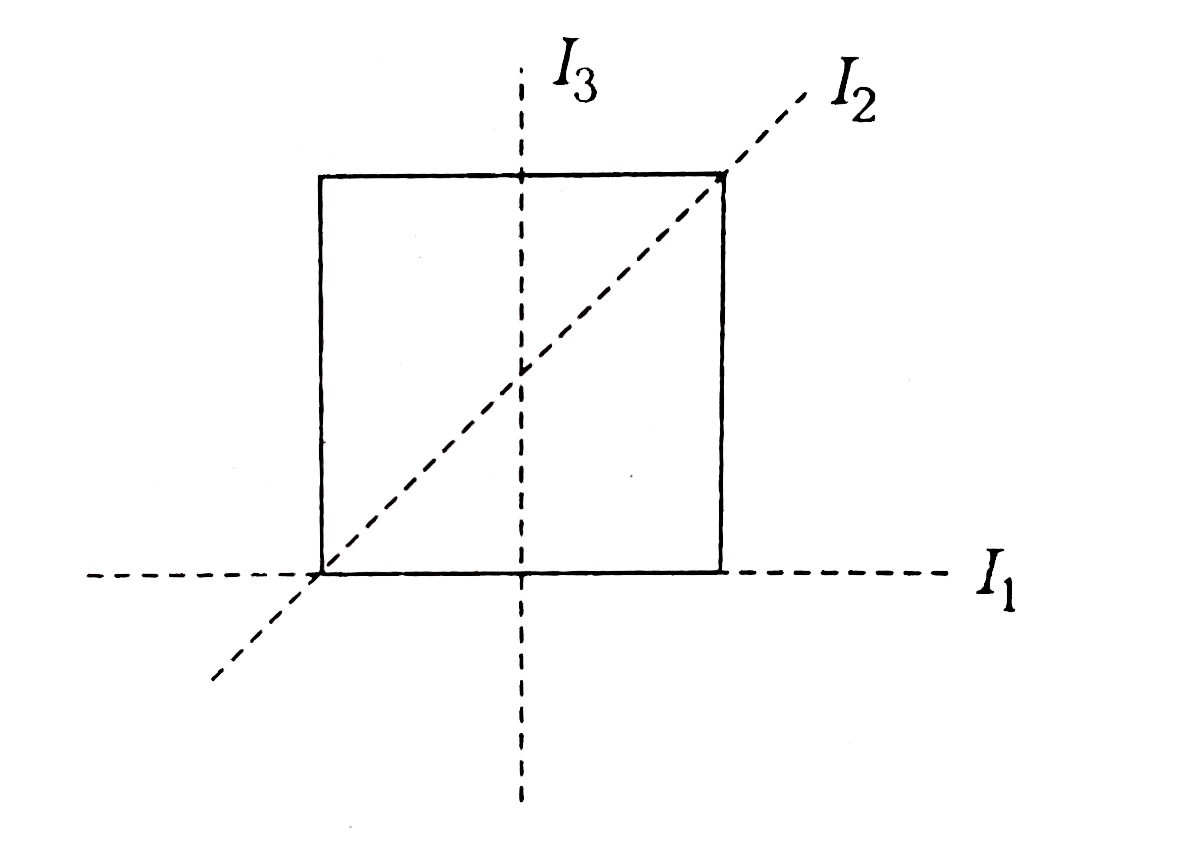 07:45View Solution
07:45View SolutionThe ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and a circular ring of the same radius about a tengential axis in the plane of the ring is
04:10View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity `omega` . Another disc of same dimensions but of mass `(1)/(4)` M is placed gently on the first disc co-axially. The angular velocity of the system is
01:45View SolutionA ring is kept on a rough inclined surface. But the coefficient of friction is less than the minimum value required for pure rolling. At any instant of time let `K_(T) and K_(R)` be the translational and rotational kinetic energies of the ring, then
01:28View SolutionA wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is `v_(CM)`, then true statement is
 01:56View Solution
01:56View SolutionA disc is rolling without slipping on a horizontal surface with C, as its centre and Q and P the two points equidistant from C. Let `v_(P),v_(Q) and v_(C)` be the magnitudes of velocities of point P,Q and C respectively, then
 01:08View Solution
01:08View SolutionA rigid body rotates with an angular momentum L. If its rotational kinetic energy is made 4 times, its angular momentum will become
02:16View SolutionA rigid and a disc of different masses are rotating with the same kinetic energy. If we apply a retarding torque `tau` on the ring, it stops after making n revolution. After how many revolutions will the disc stop, if the retarding torque on it is also `tau` ?
03:46View SolutionWork done by friction in case of pure rolling
03:20View SolutionForces are applied on a wheel of radius 20 cm as shown in the figure. The torque produced by the forces 4 N at A, 8N at B, 6 N at C and 9N at D at angles indicated is
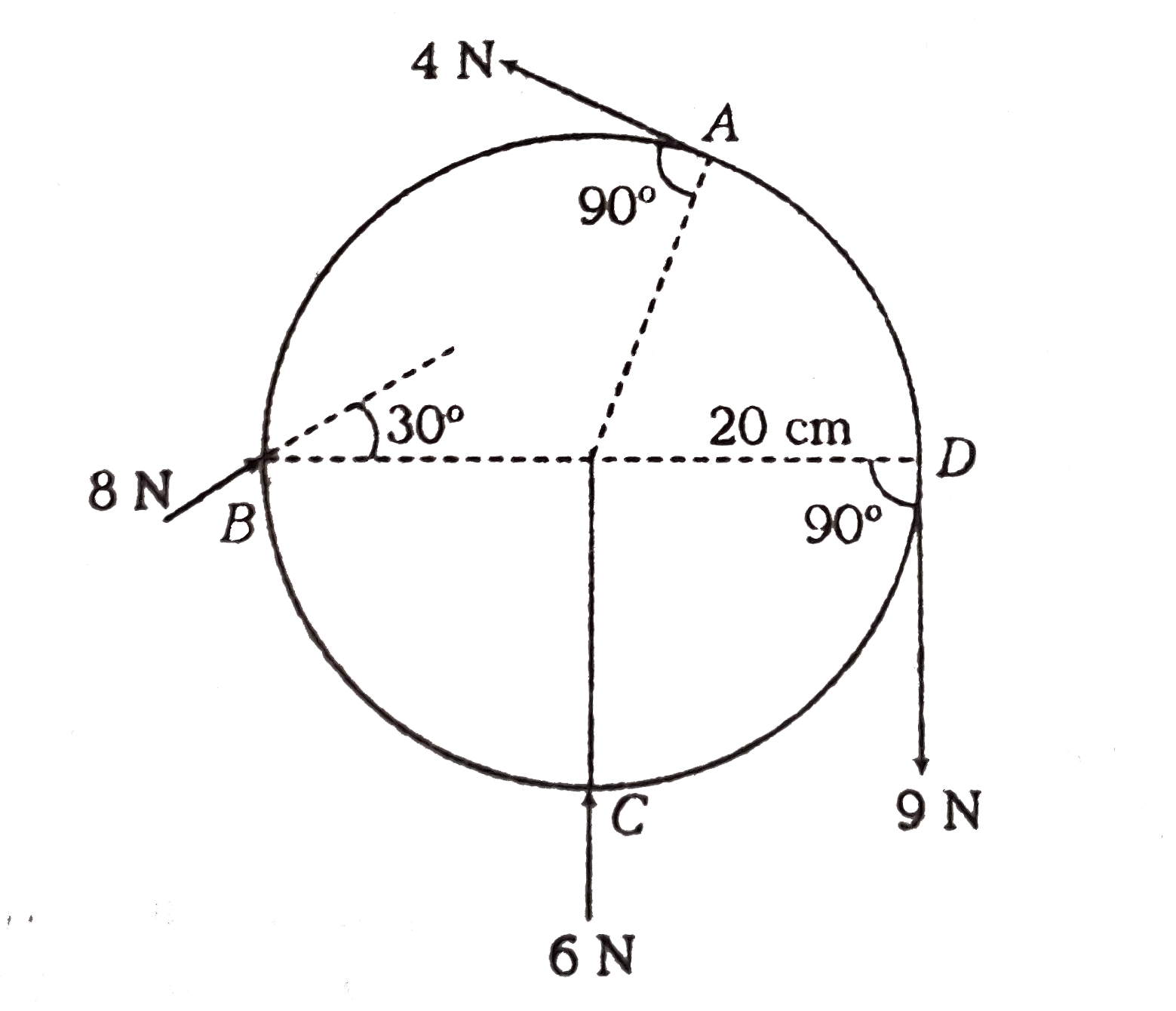 01:32View Solution
01:32View Solution`O` is the centre of an equilateral triangle `ABC`. `F_(1), F_(2)` and `F_(3)` are the three forces acting along the sides `AB, BC` and `AC` respectively. What should be the value of `F_(3)` so that the total torque about `O` is zero?
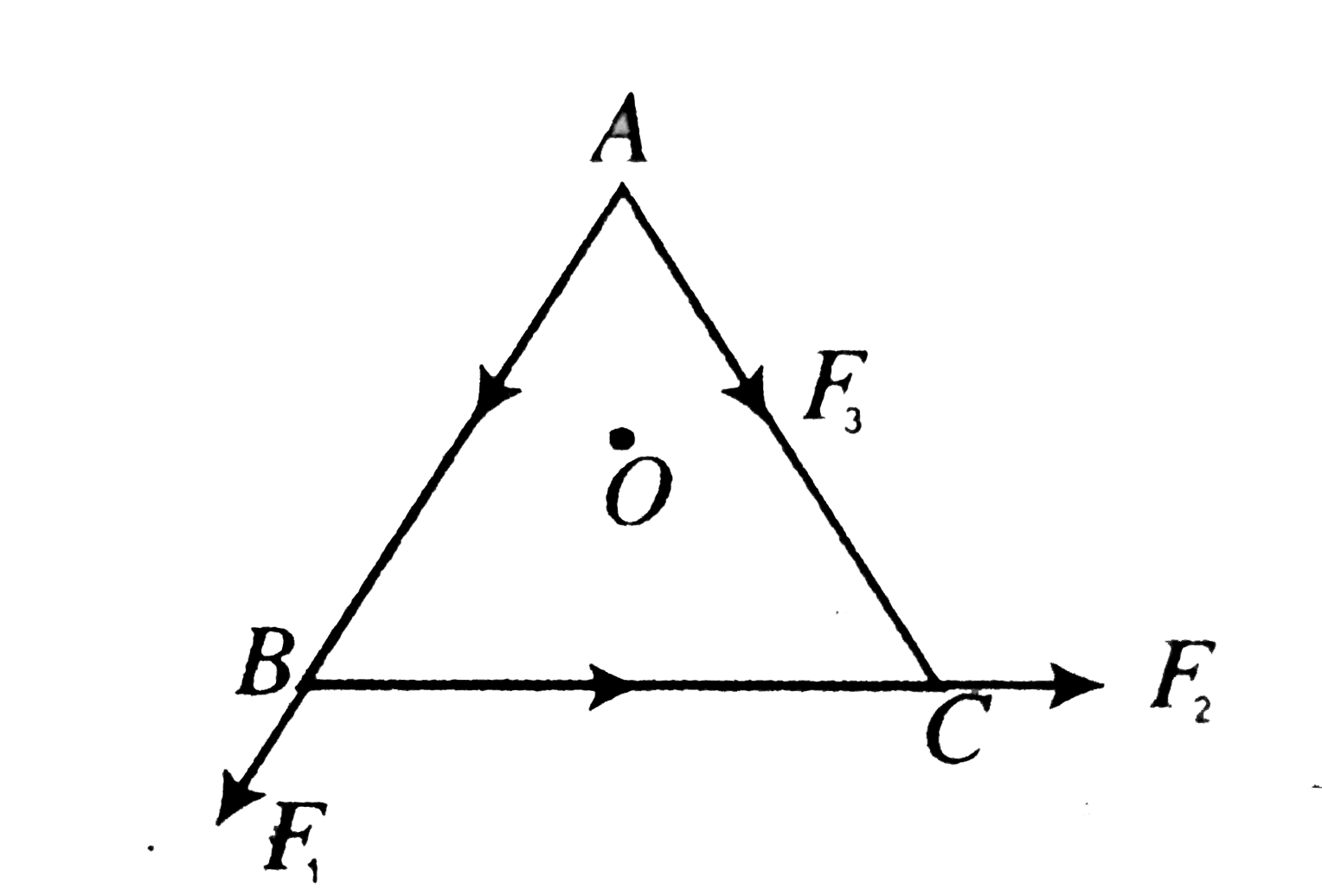 02:31View Solution
02:31View SolutionThe figure shows the angular velocity versus time graph of a flywheel. The angle, in radians through which the flywheel turns during 25 s is
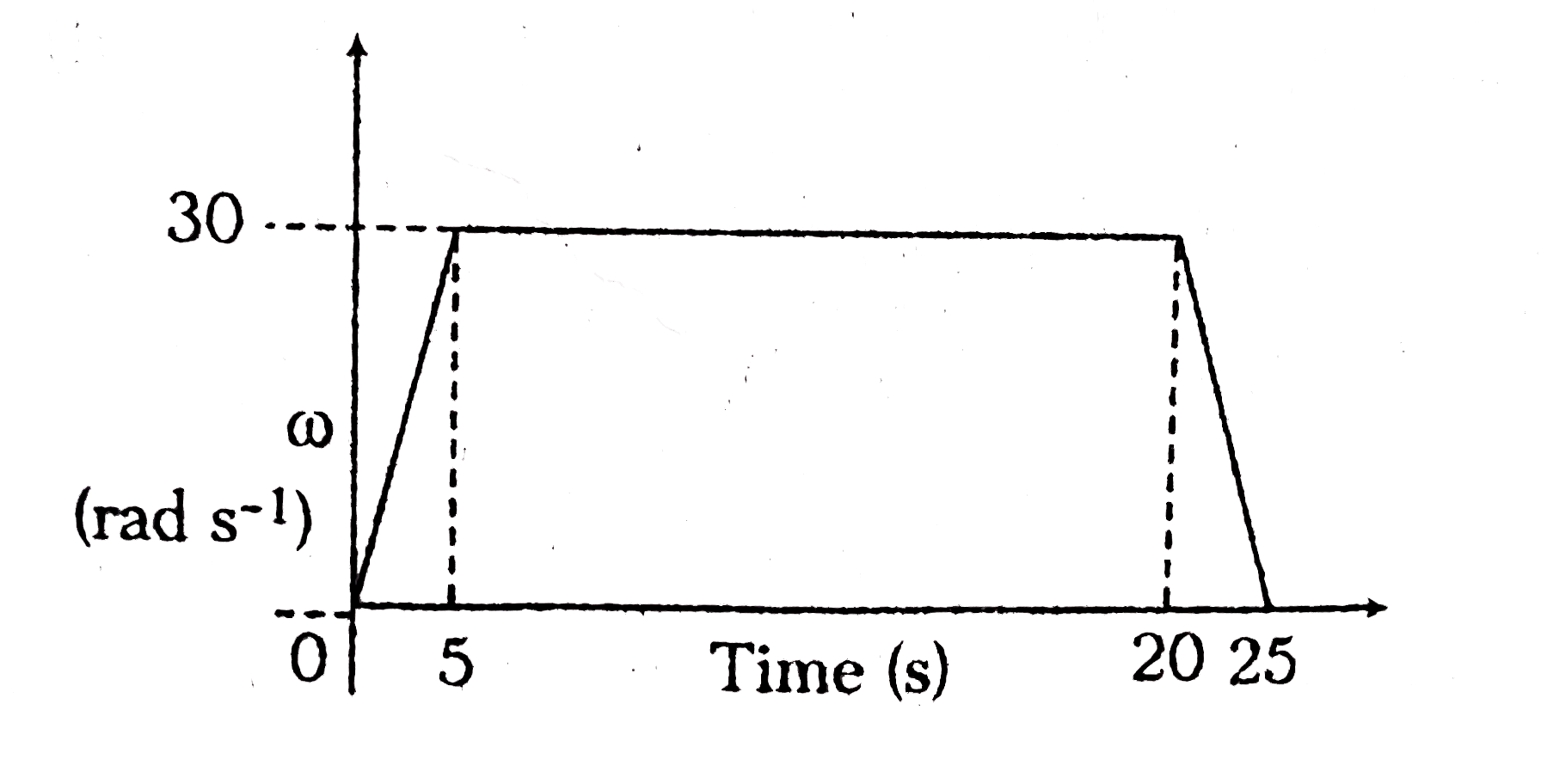 03:27View Solution
03:27View SolutionA table fan, rotating at a speed of 2400 rpm, is switched off and the resulting variation of the rpm with time is shown in the figure. The total number of revolutions of the fan before it comes to rest is
 View Solution
View SolutionA sphere can roll on a surface inclined at an angle `theta`, if the friction coefficient `mu gt (2//7)g sin theta`. Now suppose the friction coefficient is `(1//7)g sin theta` and the sphere is released from rest on the incline, then
View SolutionIf a disc of mass m and radius r is reshaped into a ring of radius`2r`, the mass remining the same, the radius of gyration about centrodal axis perpendicular to plane goes up by a factor of
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View SolutionTwo discs have same mass and thickness. Their materials are of densities `d_(1) and d_(2)`. The ratio of their moments of inertia about an axis passing through the centre and perpendicular to the plane is
View SolutionA ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is K, If radius of the ball be R, then the fraction of total energy associated with its rotational energy will be
View SolutionThe speed of a homogenous solid sphere after rolling down an inclined plane of vertical height h, from rest without sliding is
View SolutionConsider three solid spheres, sphere (i) has radius r and mass m, sphere (ii) has radius r and mass 3 m, sphere (iii) has radius 3r and mass m, All can be placed at the same point on the same inclined plane, where they will roll without slipping to the bottom, If allowed to roll down the incline, then at the bottom of the incline
View SolutionFour point masses each of value m, are placed at the corners of a square ABCD of side `l`, The moment of inertia of the system about an axis passing throught A and parallel to BD is
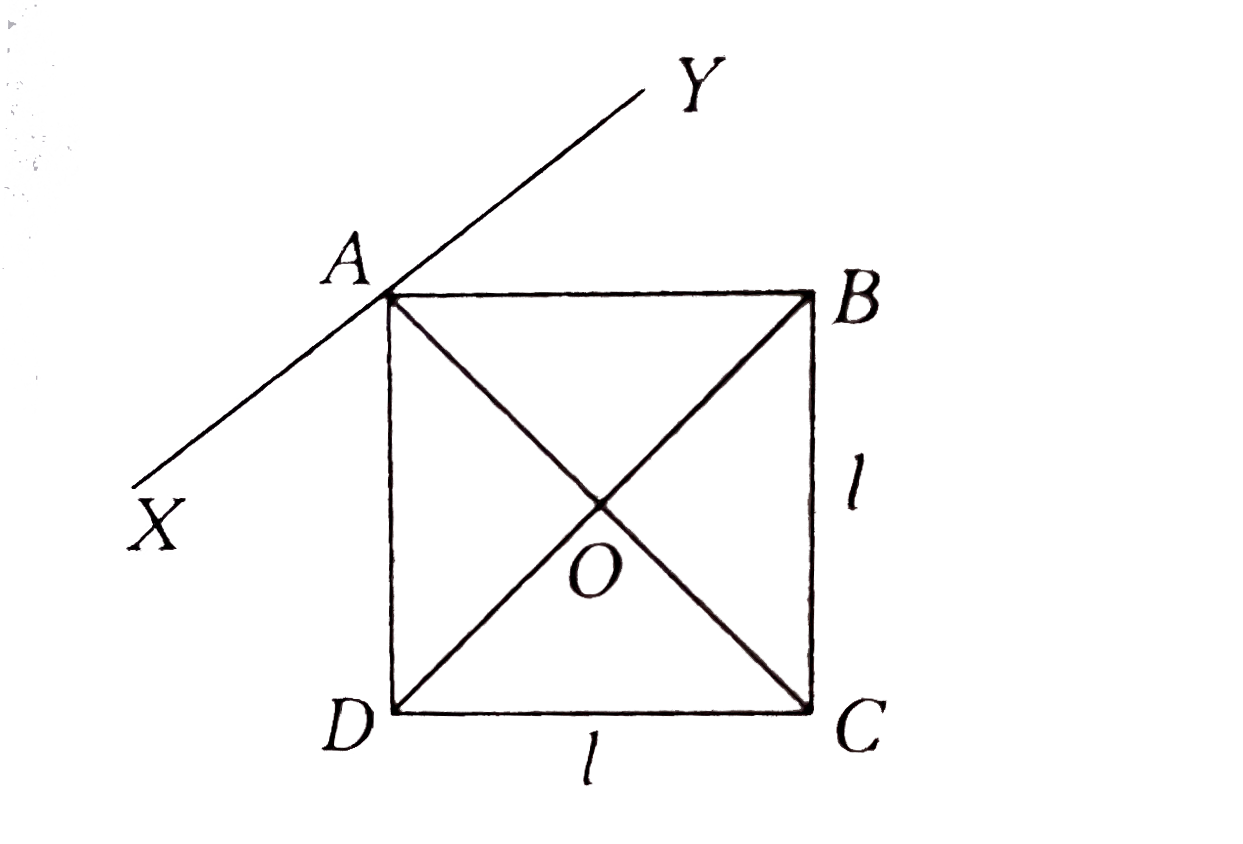 View Solution
View SolutionThe density of a non-uniform rod of length 1m is given by `rho (x)=a (1+bx^(2))` where, a and b are constant and `0 le x le 1`. The centre of mass of the rod will be at
View SolutionABC is a right angled triangular plate of uniform thickness. The sides are such that `AB gt BC` as shown in figure. `I_(1),I_(2) and I_(3)` are moments of inertia about AB,BC and AC respectively. Then, which of the following relation is correct ?
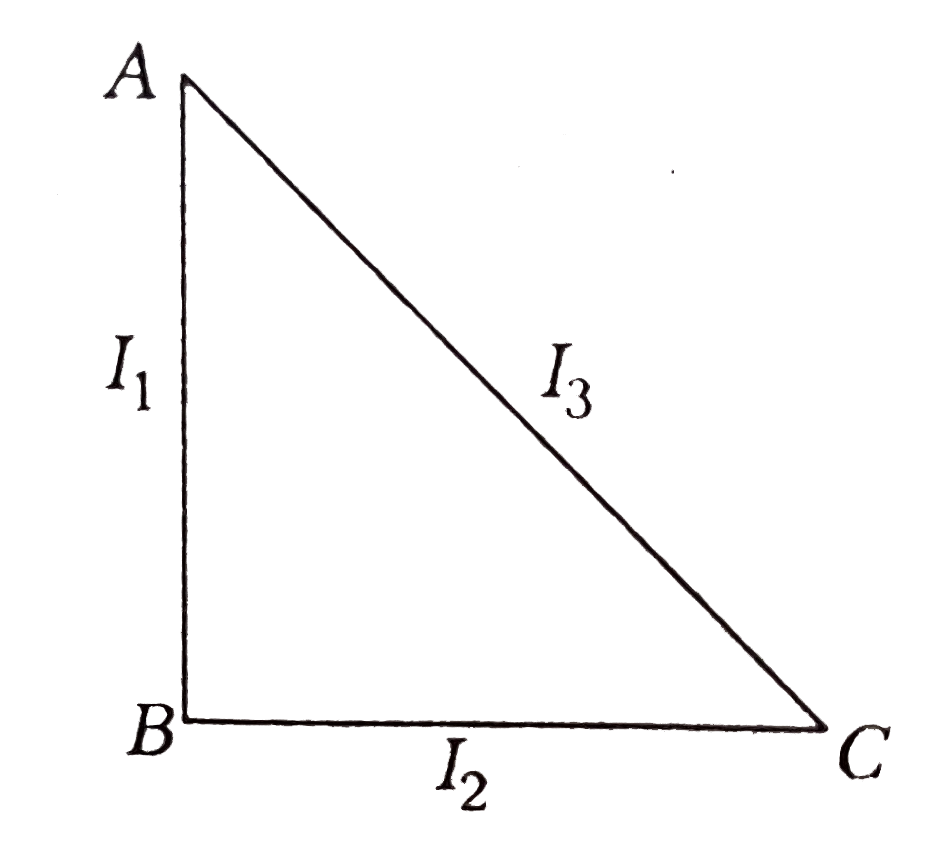 View Solution
View SolutionThe moment of inertia of a cube of mass m and side a about one of its edges is equal to
View SolutionTwo uniform, thin identical rods each of mass M and length `l` are joined together to form a cross. What will be the moment of inertia of the cross about an axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross ?
View SolutionFigure represents the moment of inertia of the solid sphere about an axis parallel to the diameter of the solid sphere and at a distance x from t. Which one of the following represents the variations of `I` with `x` ?
01:08View SolutionWhen a body is projected at an angle with the horizontal in the uniform gravitational field of the earth, the angular momentum of the body about the point of projection, as it proceeds along its path
02:54View SolutionA disc of radius R rolls on a rough horizontal surface. The distance covered by the point A in one revolution is
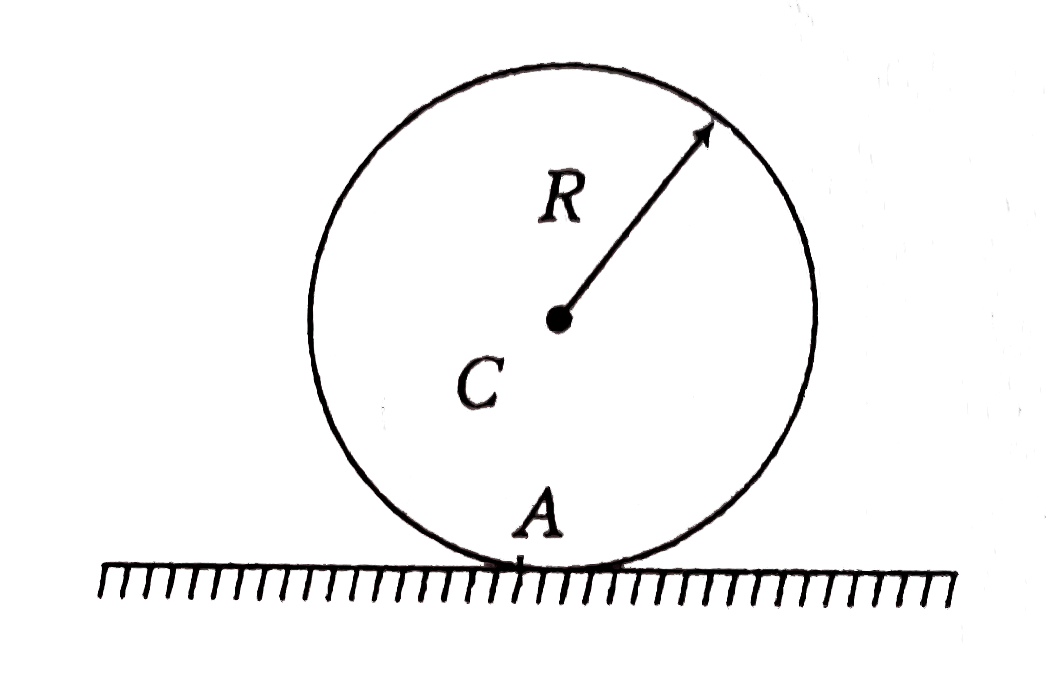 View Solution
View SolutionA uniform rod of mass 2 kg and length 1 m lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of `2 ms^(-1)` perpendicular to the length of the rod strikes it at a distance `(1)/(4)`m from the centre and stops. What is the angular velocity of the rod about its centre just after the collision ?
02:13View SolutionA particle P is moving in a circle of radius a with a uniform speed u, C is the centre of the circle and AB is a diameter. The angular velocities of P about A and C are in the ratio
View SolutionFor the uniform T shaped structure, with mass 3M, moment of inertia about an axis normal to the plane and passing through O would be
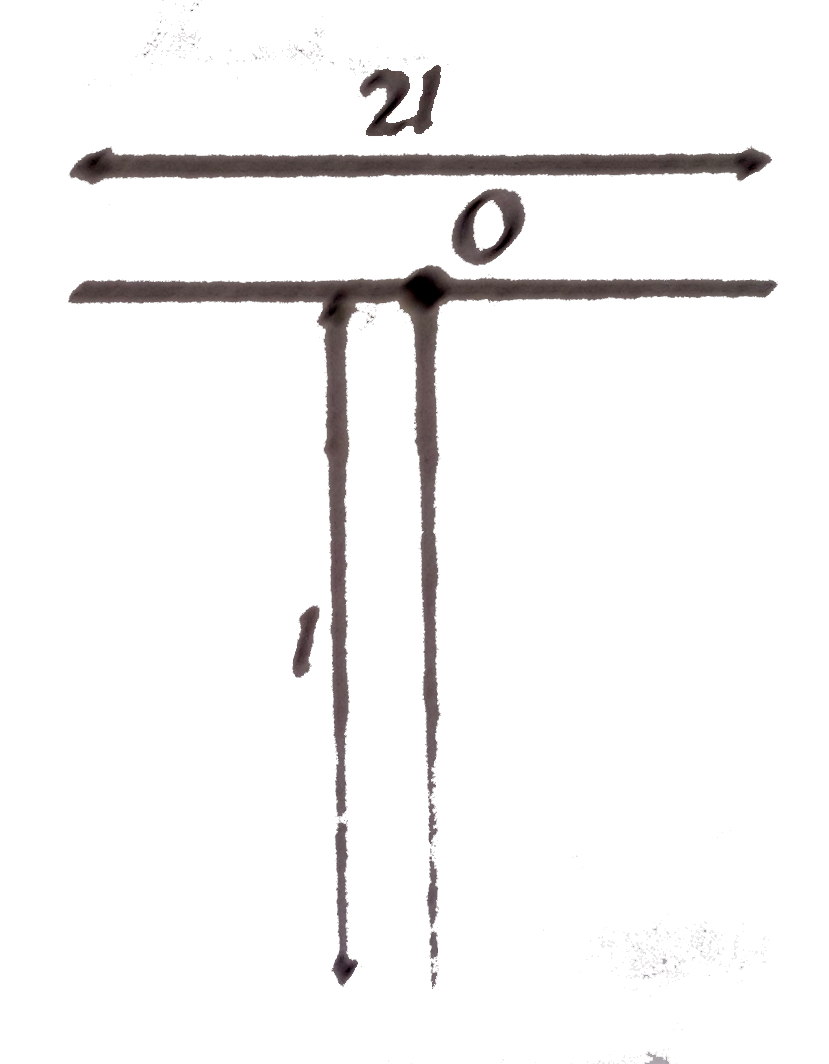 View Solution
View SolutionA wheel comprises a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is
 View Solution
View SolutionA square is made by joining four rods each of mass M and length L. Its moment of inertia about an axis PQ, in its plane and passing through one of its corner is
 02:20View Solution
02:20View SolutionA solid homogeneous sphere is moving on a rough horizontal surface, partly rolling and partly sliding. During the king of motion of the sphere.
06:03View SolutionA sphere cannot roll on
01:48View SolutionA thin bar of mass `m` and length `l` is free to rotate about a fixed horizontal axis through a point at its end. The bar is brought to a horizontal position. `(theta = 90^(@))` and then released. The angular velocity when it reaches the lowest point is
View SolutionA disc is free to rotate about a smooth horizontal axis passing through its centre of mass. A particle is fixed at the top of the disc. A slight push is given to the disc and it starts rotating. During the process.
 View Solution
View SolutionA rod of length L whose lower end is fixed along the horizontal plane starts to topple from the vertical position. The velocity of the upper end of the rod when it hits the ground is
View SolutionA solid sphere and a solid cylinder of same mass are rolled down on two inclined planes of heights `h_(1) and h_(2)` respectively. If at the bottom of the plane the two objects have same velocities, then the ratio of `h_(1) : h_(2)` is
View SolutionA solid sphere of mass 2 kg rolls up a `30^(@)` incline with an initial speed of `10 ms^(-1)`. The maximum height reached by the sphere is `(g = 10 ms^(-2))`
View SolutionThe figure shows a uniform rod lying along the X-axis. The locus of all the points lying on the XY-plane, about which the moment of inertia of the rod is same as that about O is
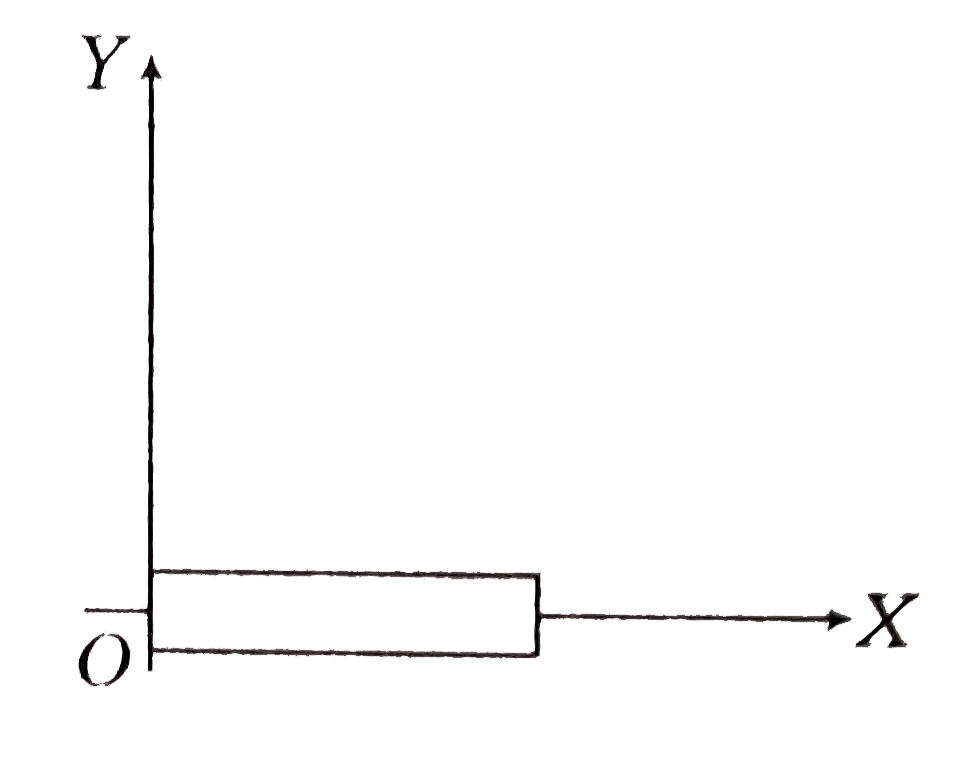 View Solution
View SolutionA cord is wound around the circumference of wheel of radius r. The axis of the wheel is horizontal and `MI` is `I`. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h, the angular velocity of the wheel will be
View SolutionA solid sphere rolls without slipping and presses a spring of spring constant `k` as shown in figure. Then, the compression in the spring will be
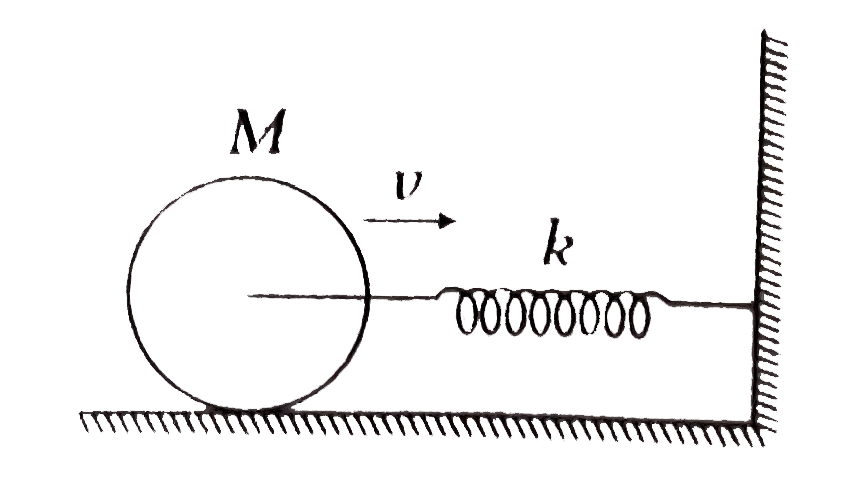 03:59View Solution
03:59View SolutionTwo uniform rods of equal length but different masses are rigidly joined to form an L-shaped body, which is then pivoted as shown in figure. If in equilibrium the body is in the shown configuration, ratio `M//m` will be
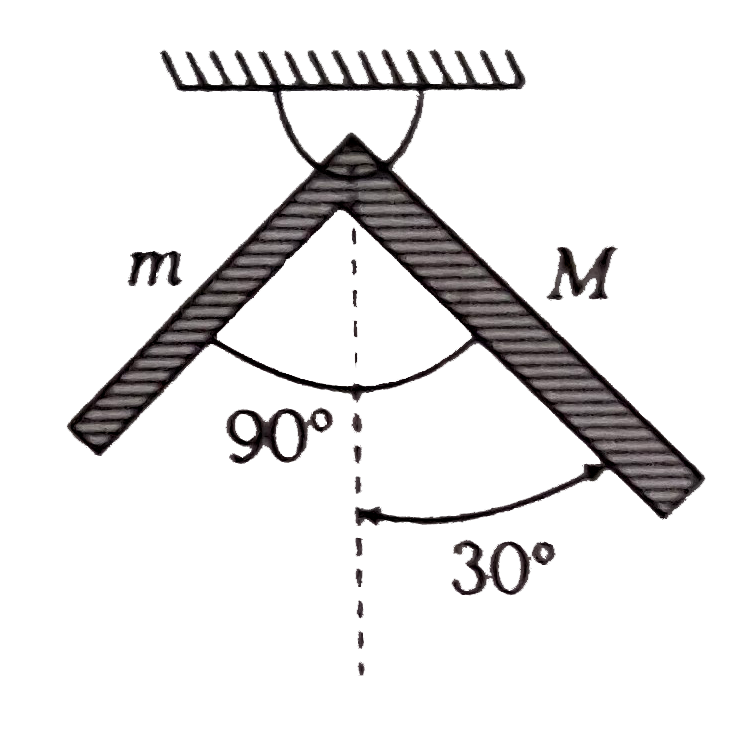 View Solution
View SolutionA portion of a ring of radius R has been removed as shown in figure. Mass of the remaining portion is `m`. Centre of the ring is at origin O. Let `I_(A) and I_(O)` be the moment of inertia passing through points A and O are perpendicular to the plane of the ring. Then,
 01:17View Solution
01:17View SolutionThe moment of inertia of a semicircular ring of mass M and radius R about an axis which is passing through its centre and at an angle `theta` with the line joining its ends as shown in figure is
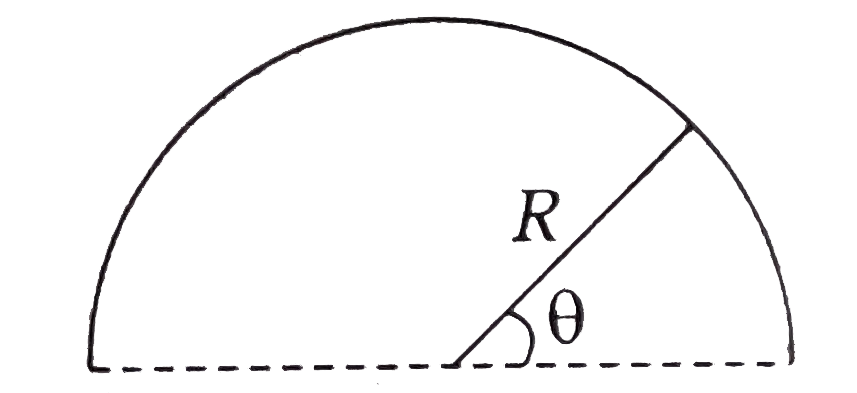 View Solution
View Solution
(A) Chapter Exercises questions and complete solutions for chapter ROTATION of DC PANDEY PHYSICS (HINGLISH) of Class 11
