Complete Solutions to (B) Chapter Exercises of chapter ROTATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATION |
| DC PANDEY NEET | (B) Chapter Exercises |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
Assertion : Moment of inertia about an axis passing throught centre of mass is always minimum
Reason : Theorem of parallel axis can be applied for 2-D as well as 3-D bodies.03:43View SolutionAssertion : A body is moving along a circle with a constant speed. Its angular momentum about the centre of the circle remains constant
Reason : In this situation, a constant non-zero torque acts on the body.04:41View SolutionAssertion : The angular velocity of a rigid body in motion is defined for the whole body
Reason : All points on a rigid body performing pure rotational motion are having same angular velocity.06:39View SolutionAssertion : If a particle is rotating in a circle, then angular momentum about centre is mvR
Reason : In circular motion, angular momentum about centre is always constant.04:56View SolutionAssertion : If we draw a circle around the centre of mass of a rigid body, then moment of inertia about all parallel axes passing through any point on this circle has a constant value.
Reason : Dimensions of radius gyration are `[M^(0)L T^(0)]`03:50View SolutionAssertion : The condition of equilibrium for a rigid body is
Translational equilibrium `Sigma F=0` and
Rotational equilibrium `Sigma tau=0`
Reason : A rigid body musy be in equilibrium under the action of two equal and opposite forces.03:07View SolutionAssertion : Two axes AB and CD are as shown in figure. Given figure is of a semi-circular ring. As the axis moves from AB towards CD, moment of inertia first decreases, then increases.

Reason : Centre of mass lies somewhere between AB and CD.01:48View SolutionAssertion : If a particle moves with a constant velocity, then angular momentum of this particle about any point remains constant.
Reason : Angular momentum has the units of Plank's constant.02:06View SolutionAssertion : Two identical solid spheres are rotated frm rest to same angular velocity `omega` about two different axes as shown in figure. More work will have to be done to rotate the sphere in case-2
Reason : Moment of inertia is case-2 is more.
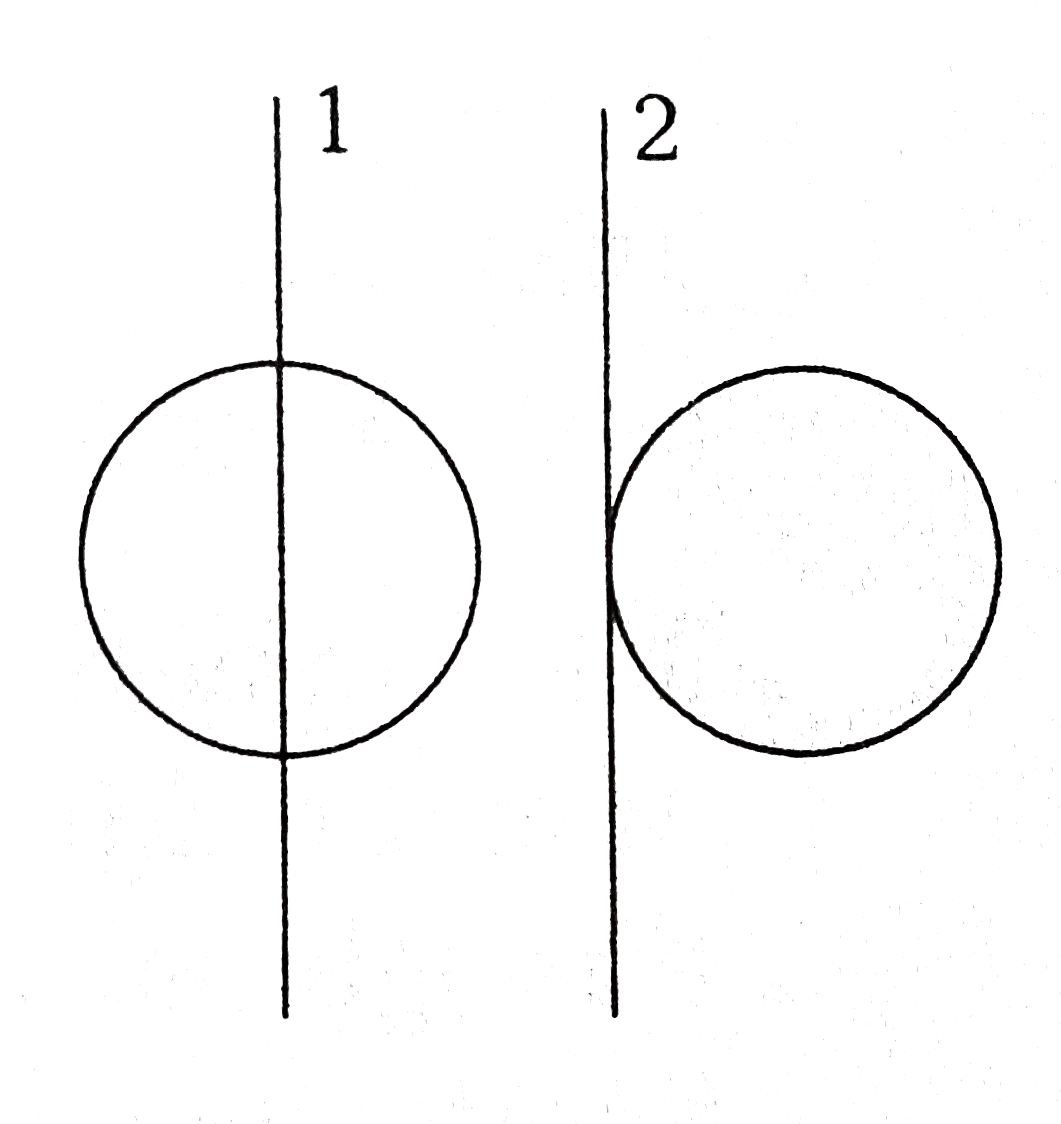 02:05View Solution
02:05View SolutionAssertion : A ring and a disc of same mass and radius begin to roll without slipping from the top of an inclined surface at `t=0`. The ring reaches the bottom of incline in time `t_(1)` while the disc reaches the bottom in time `t_(2)`, then `t_(1) lt t_(2)`
Reason : Disc will roll down the plane with more acceleration because of its lesser value of moment of inertia.02:23View SolutionAssertion : A sphere is placed in pure rolling condition over a rough inclined surface.Then, force of friction will act in downward direction

Reason : Angular acceleration (actually retardation) due to friction is anti-clockwise.02:20View SolutionAssertion : In rotational plus translational motion of a rigid body, different particles of the rigid body may have different velocities but they will have same accelerations
Reason : Translational motion of a particle is equivalent to the translation motion of a rigid body.02:22View SolutionAssertion : Angular momentum of sun and planet system about any point remains constant
Reason : Two equal and opposite forces will acts on them. Net torque of these two set of forces about any point is zero.02:01View SolutionAssertion : Moment of inertia about an axis passing throught centre of mass is always minimum
Reason : Theorem of parallel axis can be applied for 2-D as well as 3-D bodies.03:43View SolutionAssertion : A solid sphere cannot roll without slipping on smooth horizontal surface
Reason : If the sphere is left free on smooth inclined surface. It cannot roll without slipping.02:40View SolutionAssertion : Speed of any point on rigid body executing rolling motion can be calculated by expression `v =r omega`, where r is distance of point from intantaneous centre of rotation
Reason : Rolling motion of rigid body can be considered as a pure rotation about instantaneous centre of rotation.04:12View SolutionAssertion : A solid sphere and a ring of same mass and radius are released simultaneously from the top of an inclined surface. The two objects roll down the plane without slipping. They reach the bottom of the incline with equal linear speeds
Reason : Decrease in potential enery for both is the same.03:03View SolutionAssertion : A uniform disc of radius R is performing impure rolling motion on a rough horizontal plane as shown in figur. After some time the disc comes to rest. It is possible only when `v_(0) = (omega_(0)R)/(2)`

Reason : For a body performing pure rolling motion, the angular momentum uis conserved about any point in space.02:40View SolutionAssertion : Two identical spherical balls are released from two inclined plane. First is sufficiently rough and second is smooth. Both the balls will have same kinetic energy on reaching the bottom
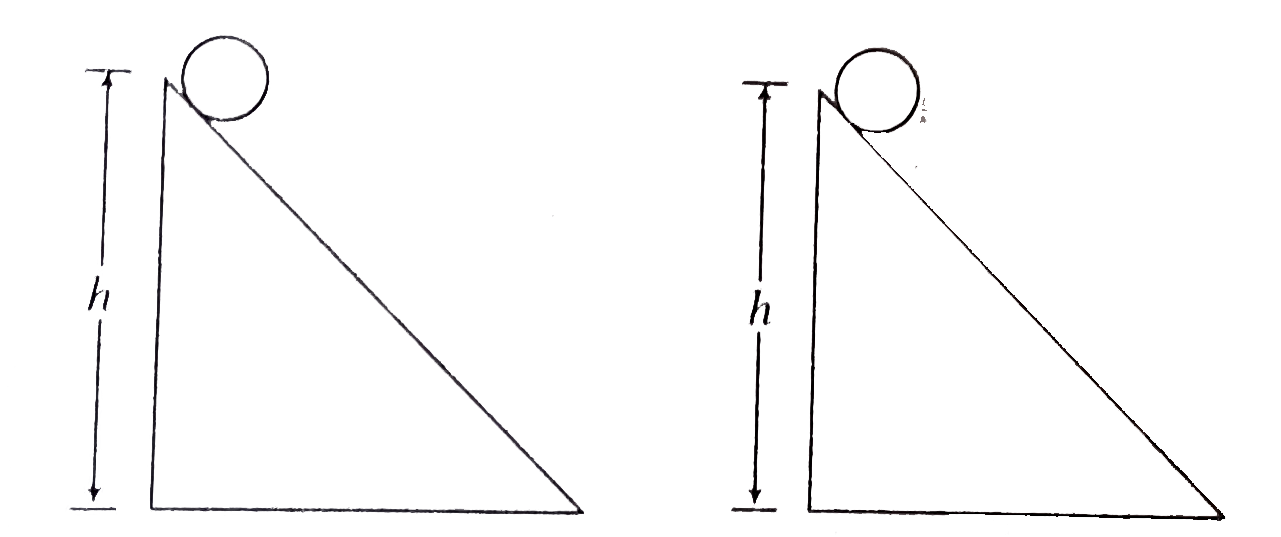
Reason : Linear velocity of second ball will be more.02:52View SolutionAssertion : A solid and a hollow sphere both of equal masses and radii are put on a rough surface after rotating with some angular velocity say `omega_(0)`. Coefficient of friction for both the spheres and ground is same. Solid sphere will start pure rolling first
Reason : Radius of gyration of hollow sphere about an axis passing through its centre of mass is more.03:17View SolutionIf radius if earth is reduced to half without changing its mass, then match the following columns
`{:(,"Column-I",,"Column-II"),("(A)","Angular momentum of earth","(p)","Will become two times"),("(B)","Time period of rotation of earth","(q)","Will become four times"),("(C)","Rotational kinetic energy of earth","(r)","Will remain constant"),("(D)",,"(s)","None"):}`03:55View SolutionA disc rolls on ground without slipping. Velocity of centre of mass is `v`. There is a point P on circumference of disc at angle `theta`. Suppose, `v_(P)` is the speed of this point. Then, match the following columns
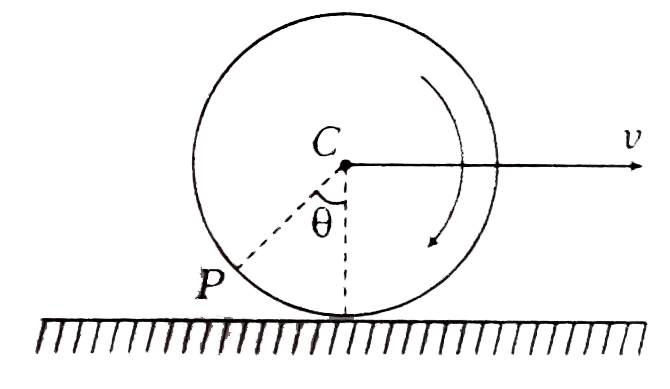
`{:(,"Column-I",,"Column-II"),("(A)","If" theta=60^(@),"(p)",v_(P)=sqrt(2)v),("(B)","If" theta=90^(@),"(q)",v_(P)=v),("(C)","If" theta=120^(@),"(r)",v_(P)=2v),("D)","If" theta=180^(@),"(s)",v_(P)=sqrt(3)v):}`View SolutionA solid sphere is rotating about an axis shown in figure. An insect follows the dotted path on the circumference of sphere as shown in the figure.
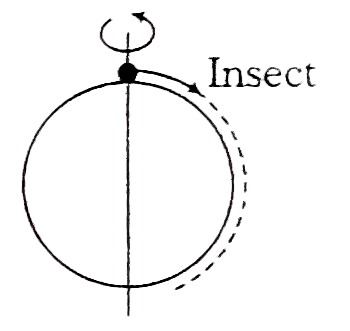
`{:(,"Column-I",,"Column-II"),("(A)","Moment of inertia","(p)","Will remain constant"),("(B)","Angular velocity","(q)","Will first increase, then decrease"),("(C)","Angular momentum","(r)","Will first decrease then increase"),("(D)","Rotational kinetic energy","(s)","Will continuously decrease"),(,,"(t)","Will continuously increase"):}`02:54View SolutionFour rods of equal length `l` and mass m each forms a square as shown in figure
Moment of inertia about three axes 1,2 and 3 are say `I_(1),I_(2) and I_(3)`. Then, match the following columns

`{:(,"Column-I",,"Column-II"),("(A)",I_(1),"(p)",(4)/(3)ml^(2)),("(B)",I_(2),"(q)",(2)/(3)ml^(2)),("(C)",I_(3),"(r)",(1)/(2)ml^(2)),(,,"(s)","None"):}`04:41View SolutionA semicircular ring has mass m and radius R as shown in figure. Let `I_(1),I_(2),I_(3) and I_(4)` be the moments of inertia of the four axes as shown. Axis 1 passes through centre and is perpendicular to plane of ring. Then, match the following columns.

`{:(,"Column-I",,"Column-II"),("(A)",I_(1),"(p)",(mR^(2))/(2)),("(B)",I_(2),"(q)",(3//2)mR^(2)),("(C)",I_(3),"(r)",mR^(2)),("(D)",I_(4),"(s)","Data is insufficient"):}`04:30View Solution
(B) Chapter Exercises questions and complete solutions for chapter ROTATION of DC PANDEY PHYSICS (HINGLISH) of Class 11
