Complete Solutions to Solved Examples of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| DC PANDEY | Solved Examples |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
Three particles, each of the mass `m` are situated at the vertices of an equilateral triangle of side `a`. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation `a`. Find the initial velocity that should be given to each particle and also the time period of the circular motion. `(F=(Gm_(1)m_(2))/(r^(2)))`
04:01View SolutionIn the above problem, find total mechanical energy of the system .
03:18View SolutionTwo concentric shells of masses `M_(1)` and `M_(2)` are concentric as shown. Calculate the gravitational force on m due to `M_(1)` at points P,Q and `R`.
 04:48View Solution
04:48View SolutionGravitational potential energy between two points masses is
`U = -(Km_(1)m_(2))/(r^(n))`
where, `K` is a positive constant. With what power of 'r' time period of a satellite of mas 'm' varies in circular orbit if mass of planet is `M` ?02:36View SolutionImagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. if the gravitational force of attraction between the planet and the star is proportational to `R^(-5//2)`, then
(a) `T^(2)` is proportional to `R^(2)`
(b) `T^(2)` is proportional to `R^(7//2)`
(c) `T^(2)` is proportional to `R^(3//3)`
(d) `T^(2)` is proportional to `R^(3.75)`.01:54View SolutionThere is a smooth tunnel upto centre C of a solid sphere of mass 'M' and radius R.A particle of mass `m(ltltM)` is realeased from point P along the line CP. Find velocity of 'm' while striking at `C`.
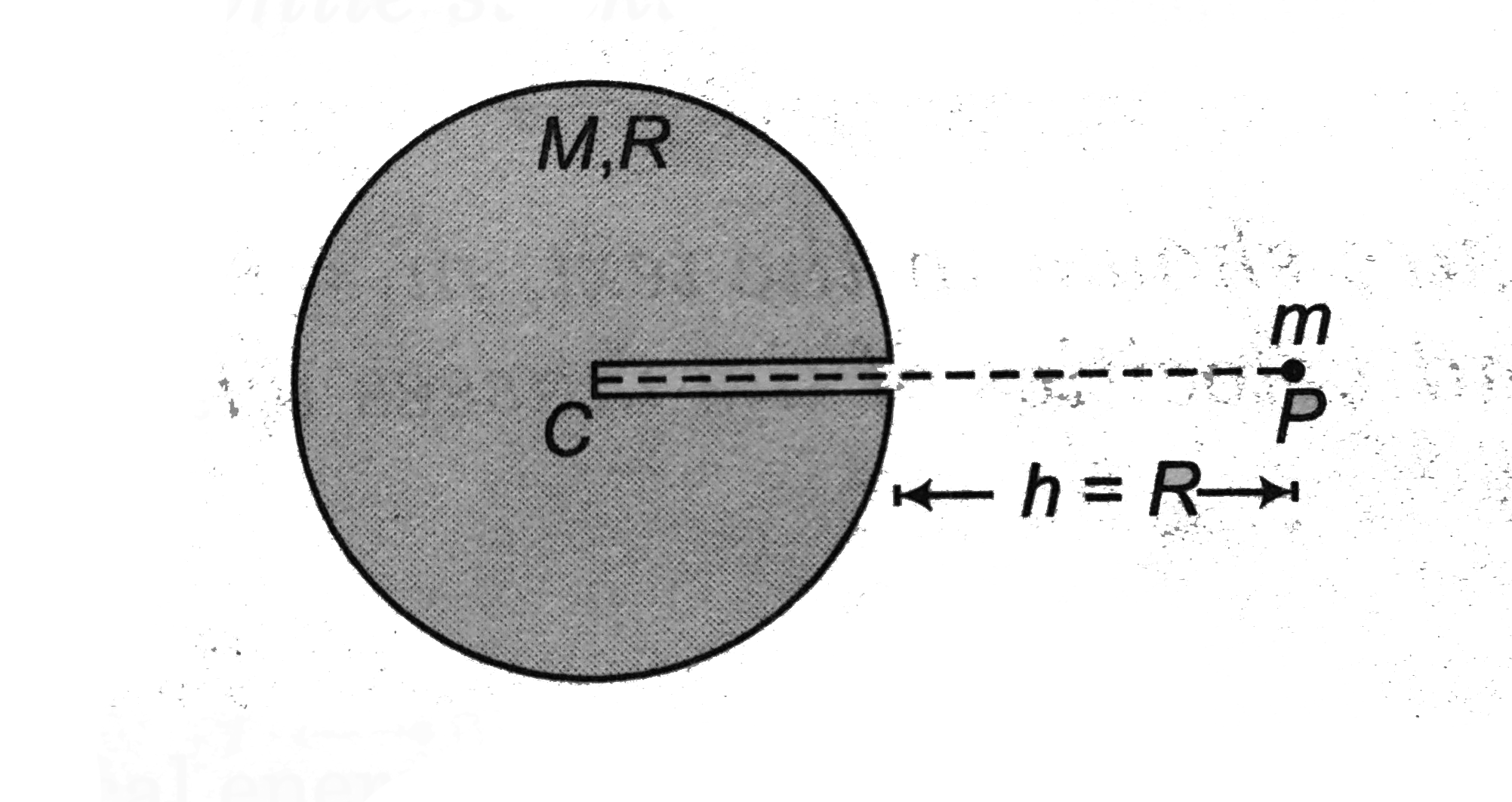 .02:51View Solution
.02:51View SolutionA particle of mass 'm' is projected from the surface of earth with velocity`upsilon =2upsilon_(e)`, where `upsilon_(e)` is the value of escape velocity from the surface of earth . Find velocity of the particle on reaching to interstellar space (at infinity) in terms of `upsilon_(e)`.
05:02View SolutionIn the figure shown in text, `m_(1) = m`, `m_(2) = 2m` and initial distance between them is `r_(0)`. Find velocities of the masses when separation between them becoms `r_(0)/(2)`.
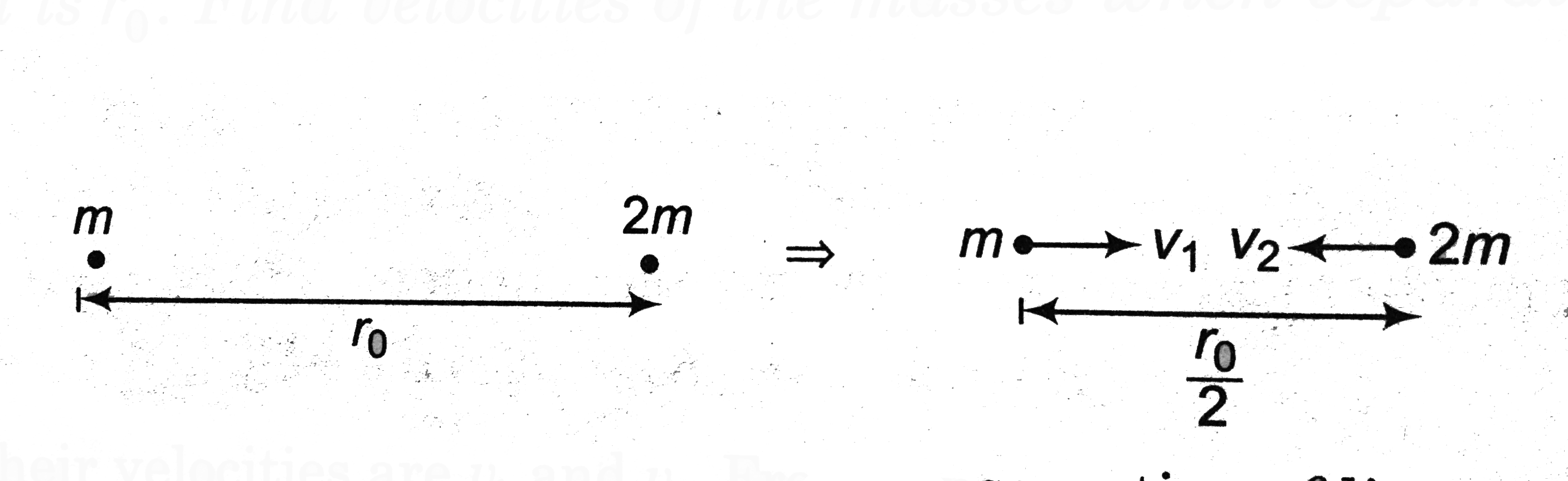 04:24View Solution
04:24View SolutionFind the maximum and minimum distances of the planet `A` from the sun `S`, if at a ceration moment of times it was at a distance `r_(0)` and travelling with the velocity `upsilon_(0)`. With the angle between the radius vector and velocity vector being equal to `phi`.
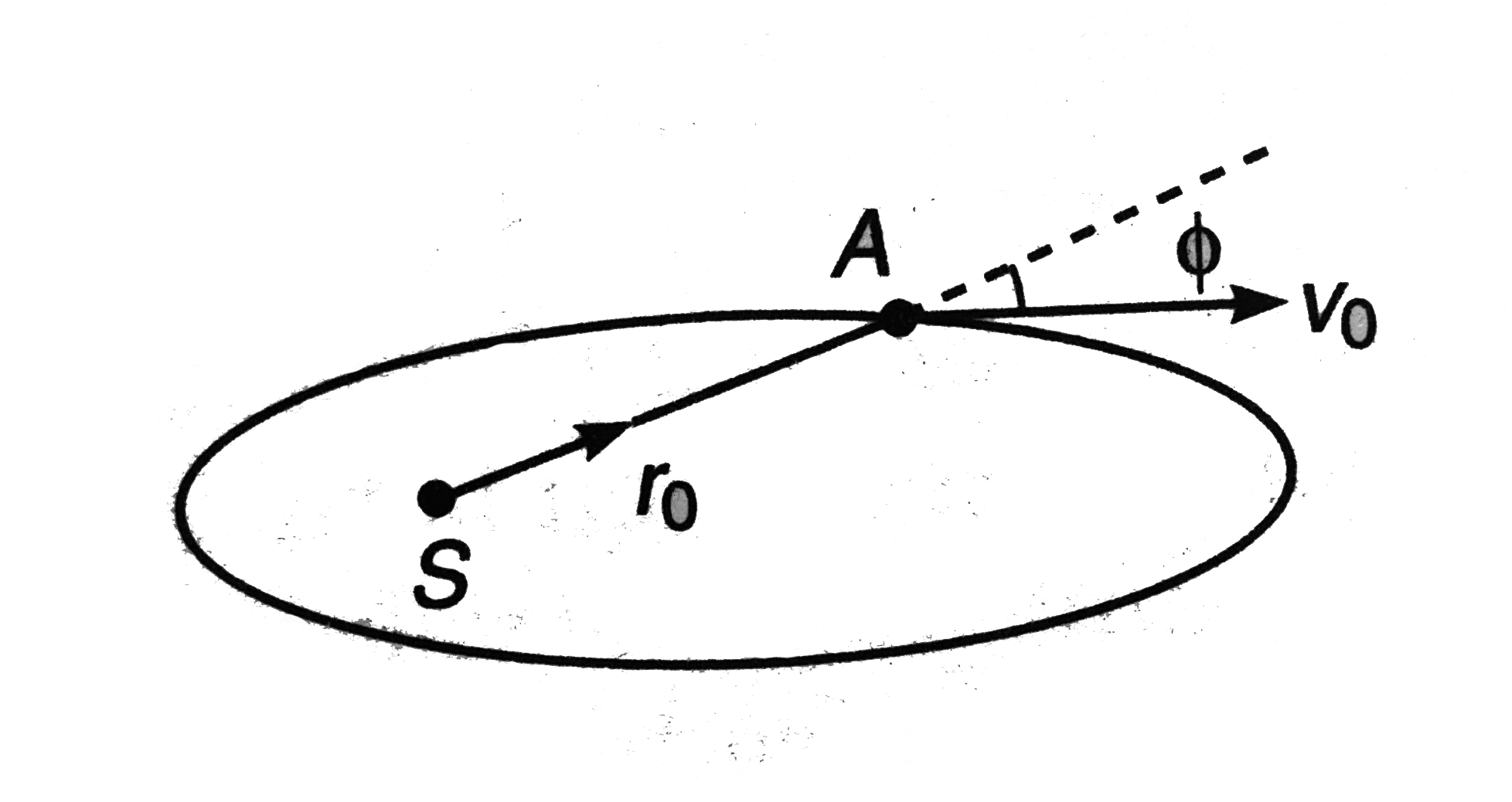 06:49View Solution
06:49View SolutionA projectile of mass `m` is fired from the surface of the earth at an angle `alpha = 60^(@)` from the vertical. The initial speed `upsilon_(0)` is equal to `sqrt((GM_(e))/(R_(e))`. How high does the projectile rise ? Neglect air resistance and the earth's rotation.
02:45View SolutionA plant of mass `m_(1)` revolves round the sun of mass `m_(2)`. The distance between the sun the planet is `r`. Considering the motion of the sun find the total energy of the system assuming the orbits to be circular.
06:35View SolutionIn the problem discussed in the text, find `E - r` expressions for inside and outside points.
03:32View SolutionTwo points masses 'm' and `2m` are kept at certain distance as shows in figure. Draw `E - r` and `V - r` graphs along the line joining them corresponding to given mass system.
 06:14View Solution
06:14View SolutionIn the problem discussed in the text, find the values of `E` and `V` at `p` dua to the remaining mass.
03:01View SolutionDistance between the centres of two stars is `10a`. The masses of these stars are `M` and `16 M` ans their radit a nd `2a` respectively. A body of mass `m` is fired straight from the surface of the larger star tpwards the surface of the smaller star. What should be its minimum intial speed to reach the surface of the smaller star? Obtain the expression in terms of `G`, `M` and a.
08:13View SolutionThree spherical shells of masses `M`, `2M` and `3M` have radii `R`, `3R` and `4R` as shows in figure. Find net potential at point `P`, where `CP = 2R`.
 02:53View Solution
02:53View Solution
Solved Examples questions and complete solutions for chapter GRAVITATION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS GRAVITATION
- (A) Chapter Exercises
- (B) Chapter Exercises
- (C) Chapter Exercises
- Check Point 10.1
- Check Point 10.2
- Check Point 10.3
- Check Point 10.4
- Check Point 10.5
- Check Point 10.6
- Example
- Exercise 13.1
- Exercise 13.2
- Exercise 13.3
- Exercise 13.4
- Exercise 13.5
- Exercise 13.6
- Exercise 13.7
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Examples
