Complete Solutions to (B) Chapter Exercises of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| DC PANDEY NEET | (B) Chapter Exercises |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
Assertion : Gravitational force between two masses in air is F. If they are immersed in water, force will remain F
Reason : Gravitational force does not depend on the medium between the masses.
View SolutionAssertion : Angular momentum of a planet is constant about any point
Reason : For acting on the planet is a central force.
View SolutionAssertion : Kepler's law for planetary motion are consequence of Newton's laws
Reason : Kepler's laws can be derived by using Newton's laws.
View SolutionAssertion : The field strength at the centre of a ring is zero
Reason : At the centre of the ring, slope of V-r graph is zero.\
View SolutionAssertion : The binding energy of a satellite does not depend upon the mass of the satellite.
Reason : Binding energy is the negative value of total energy of satellite.
View SolutionAssertion : Plane of a satellite always passes through the centre of earth
Reason : Gravitational force on satellite is always towards centre of earth.
View SolutionAssertion : Gravitational potential and gravitational potentail energy, both are related to the work done by gravitational force in the gravitational field
Reason : Gravitational field strength is related to the gravitaional force in gravitational field.
View SolutionAssertion : One two sides of a point mass, gravitational field strength is same at same distance,
Reason : As we move away from a point mass, value of gravitational potential decreases.
View SolutionAssertion : If gravitational potential at some point is zero, then gravitational field strength at that point will also be zero.
Reason : Except at infinity gravitational potential due to a system of point masses at some finite distance can't be zero.
View SolutionAssertion : If radius of earth suddenly shrinks to half its present without changing its mass value, then the period of an earth's satellite will not change
Reason : Time period of a satellite does not upon the mass of earth.
View SolutionAssertion : The centres of two cubes of masses `m_(1) and m_(2)` are separated by a distance r. The gravitational force between these two cubes will be `(Gm_(1)m_(2))/(r^(2))`
Reason : According to Newton's law of gravitation, gravitational force between two point masses `m_(1) and m_(2)` separated by a distance r is `(Gm_(1)m_(2))/(r^(2))`.
View SolutionAssertion : If a particle is projected from the surface of earth with velocity equal to escape velocity, then total mechanical energy is zero
Reason : Total mechanical energy of any closed system is always negative.
View SolutionAssertion : On earth's satellite, we feel weightlessness. Moon is also satellite of earth. But on the surface on moon, we do not feel weightlessness
Reason : Gravitational force by earth on us on the surface of moon is zero. But gravitational force by moon on us on its surface is non-zero.
View SolutionAssertion : The centre of semicircular ring of mass `m` and radius R is the origin O. The potential at origin is `-(Gm)/(R)`
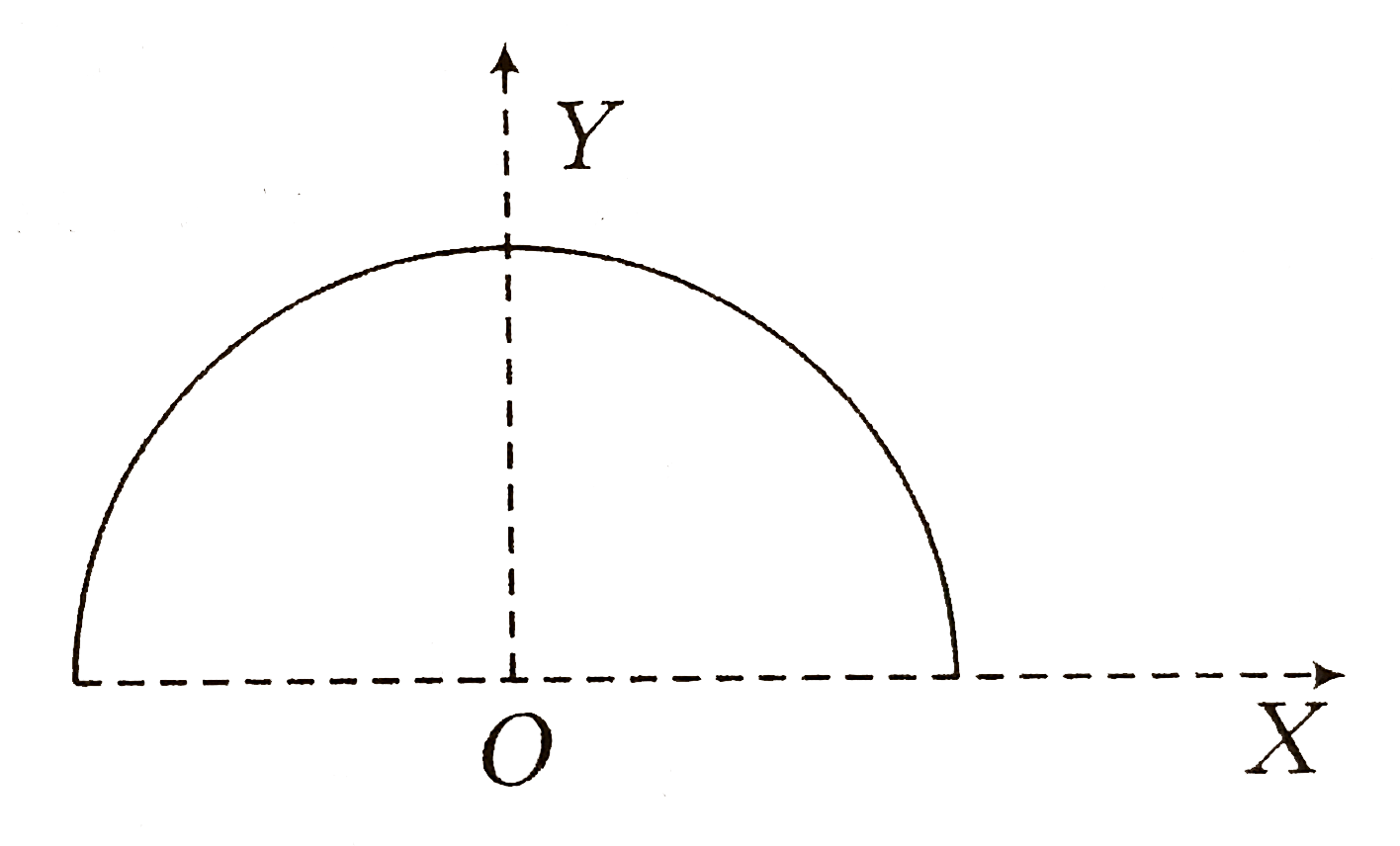
Reason : The gravitational field strength is towards Y-axis.
View SolutionAssertion : If the projuct of surface area and density is same for both
Reason : Product of surface area and density is proportional to the mass of the planet per unit radius f the planet.
View SolutionAssertion : Areal velocity of a planet around of surface area and density is same for two planets, escape velocities will be same for both
Reason : Areal velocity `= (L)/(2m)`, Where L is angular momentum of planet about centre of sun.
View SolutionAssertion : Mass of the rod AB is `m_(1)` and of particle P is `m_(2)`. Distance between centre of rod and particle is r. Then the gravitational force between the rod and the particle is
`F=(Gm_(1)m_(2))/(r^(2))`
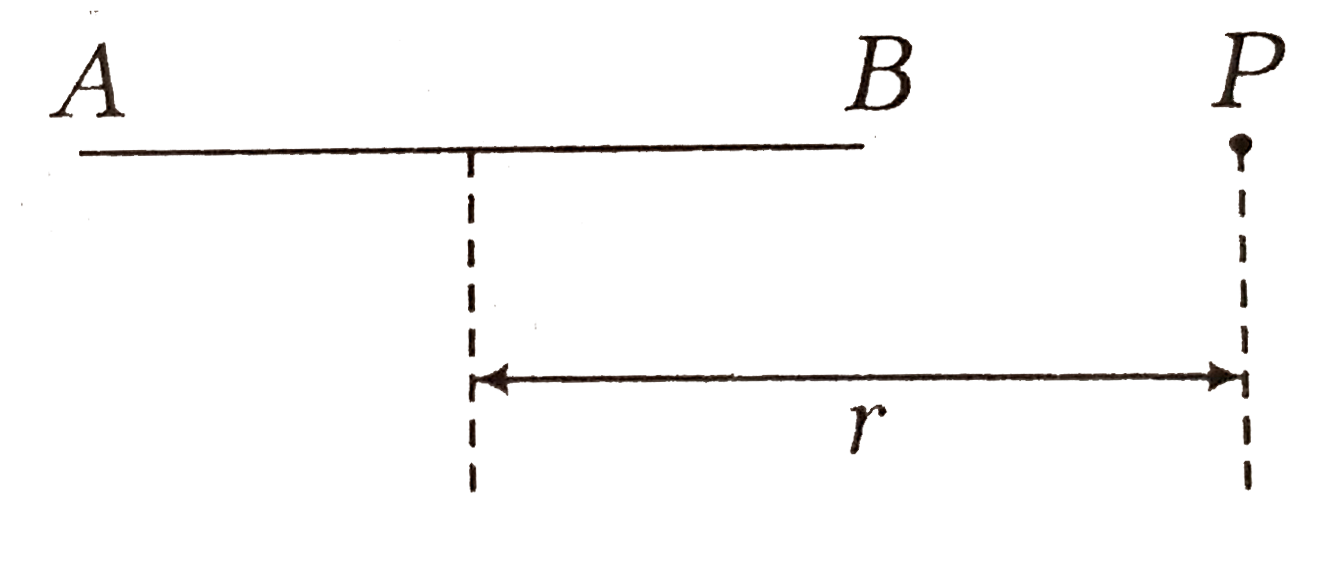
Reason : The relation `F=(Gm_(1)m_(2))/(r^(2))` can be applied directly only to find force between two particles.
View SolutionAssertion : Four point masses each of mass `m` are placed at points 1, 2, 3 and 6 of a regular hexagon of side a. Then the gravitational field at the centre of hexagon is `(Gm)/(a^(2))`
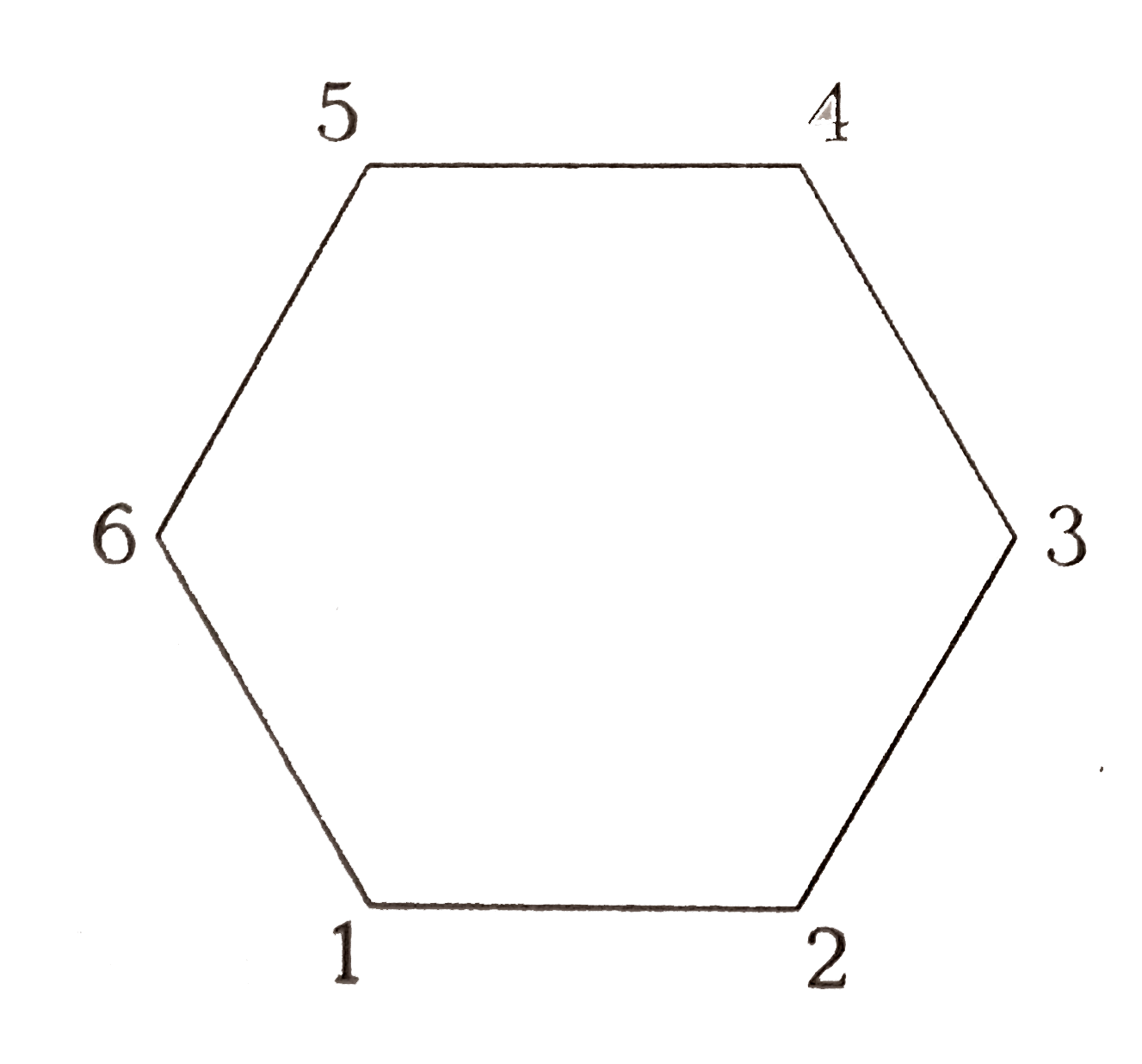
Reason : The field strength due to masses at 3 and 6 are cancelled out.
View SolutionAssertion : Let `W_(1)` be the work done in taking away a satellite from the surface of earth to its orbit and then `W_(2)` the work done in rotating the satellite in circular orbit there. Then, `W_(1)=W_(2)`
Reason : `W_(2)=(GMm)/(4R)`
View SolutionAssertion : Two spherical shells have masses `m_(1) and m_(2)`. Their radii are `r_(1) and r_(2)`. Let `r` be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for `O lt r lt r_(1)`
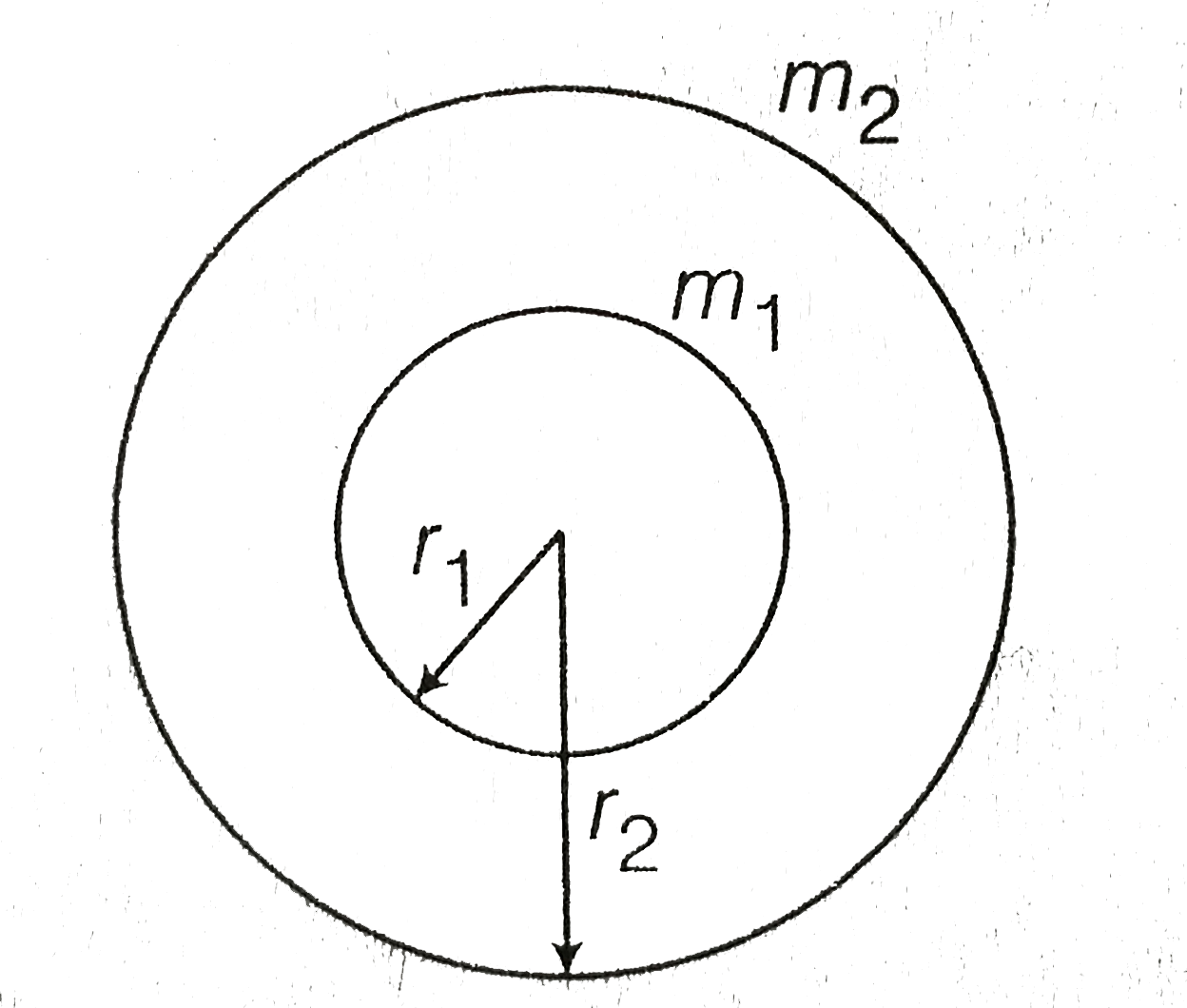
Reason : In the region `r_(1) lt r lt r_(2)`, gravitational field strength due to `m_(2)` is zero. But gravitational potential due to `m_(2)` is constant (but non-zero).
View SolutionMatch the following
`{:(,"Column-I",,"Column-II"),("(A)","Kepler's first law","(p)",T^(2)propr^(3)),("(B)","Kepler's second law","(q)","Areal velocity is constant"),("(C)","Kepler's third law","(r)","Orbit of planet is elliptical"):}`
View SolutionDensity of a planet is two times the density of earth. Radius of this planet is half. Match the following (as compared to earth)
`{:(,"Column-I",,"Column-II"),("(A)","Accleration due to gravity on this planet's surface","(p)","Half"),("(B)","Gravitational potential on the surface","(q)","Same"),("(C)","Gravitational potential at centre","(r)","Two times"),("(D)","Gravitational field strength at centre","(s)","Four times"):}`
View SolutionOn the surface of earth acceleration due gravity is `g` and gravitational potential is V. Match of following columns
`{:(,"Column-I",,"Column-II"),("(A)","At height h=R, value of g","(p)","Decreases by a factor" (1)/(4)),("(B)","At depth " h =(R)/(2)"," "value of g","(q)","Decrease by a factor" (1)/(2)),("(C)","At height "h=R",""value of V","(r)","Increase by a factor" (11)/(8)),("(D)","At height "h=(R)/(2)"," "value of V","(s)","Increase by a factor 2"),(,,"(t)","None"):}`
View SolutionLet V and E denote the gravitational potential and gravitational field at a point. Then, match the following columns
`{:(,"Column-I",,"Column-II"),("(A)",E = 0","V = 0,"(p)","At centre of spherical shell"),("(B)",E ne0","V=0,"(q)","At centre of solid sphere"),("(C)",V ne0","E=0,"(r)","At centre of circular ring"),("(D)",V ne0","E ne0,"(s)","At cetre of two point masses of equal magnitude"),(,,"(t)","None"):}`
View SolutionTwo concentric spherical shells are as shown in figure. Match the following columns
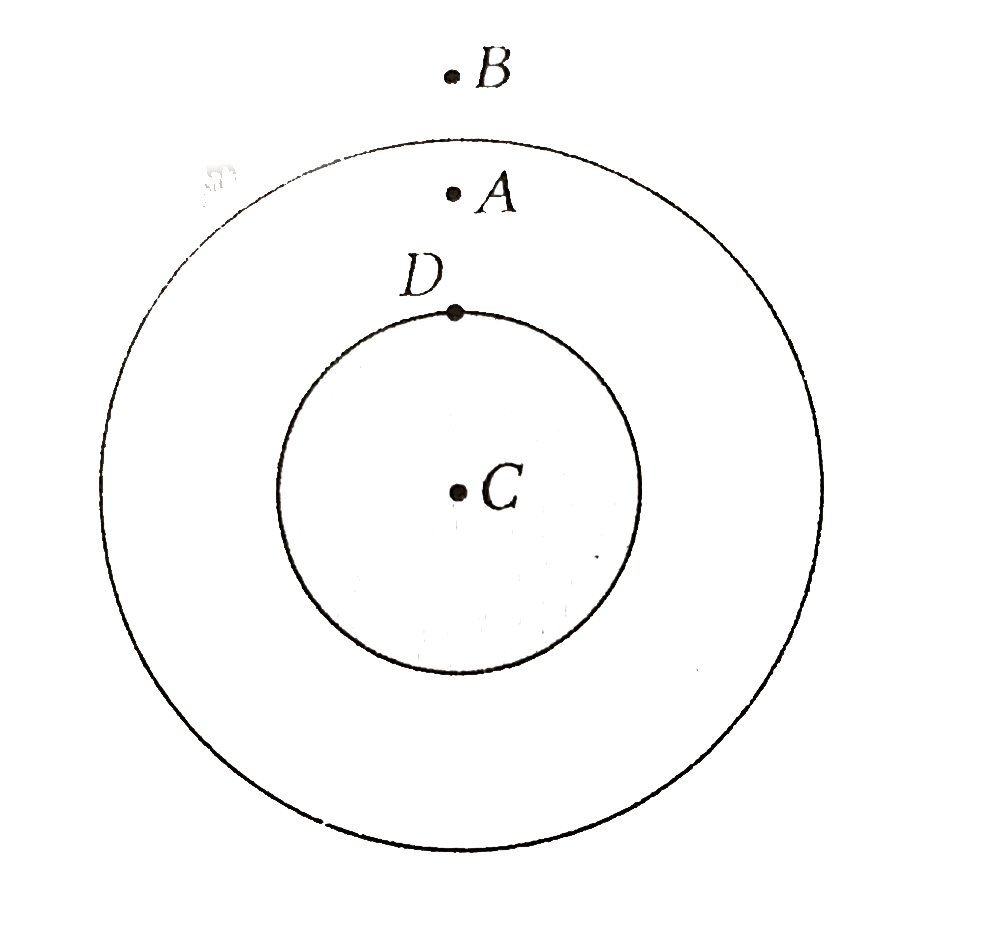
`{:(,"Column-I",,"Column-II"),("(A)","Potential at A","(p)","greater than B"),("(B)","Gravitational field at A","(q)","less than B"),("(C)","As one moves from C to D","(r)","Potential remains constant"),("(D)","As one moves from D to A","(s)","Gravitational field decreases"),(,,"(t)","None"):}`
View SolutionMatch of following columns
`{:(,"Column-I",,"Column-II"),("(A)",underset(underset("field is increasing")("particle in gravitational"))("Kinetic enery of a"),"(p)",underset(underset("be positive")("gravitational force should"))("Work done by")),("(B)",underset(underset("field is increasing")("particle in gravitational"))("Potential energy of a"),"(q)",underset("force should be non-zero")("Work done by external")),("(C)",underset(underset("field is increasing")("particle in gravitational"))("Mechanical energy of a"),"(r)",underset(underset("be negative")("gravitational force should"))("Work done by")),(,,"(s)","Cannot say anything"):}`
View SolutionA particle is projected from the surface of earth of mass M and radius R with speed `v`. Suppose it travels a distance `x(lt lt R)` when its speed becomes `v` to `v//2` and `y(lt lt R)` when speed changes from `v//2` to 0. Similarly, the corresponding times are suppose `t_(1) and t_(2)`. Then
`{:(,"Column-I",,"Column-II"),("(A)",x//y,"(p)",=1),("(B)",t_(1)//t_(2),"(r)",gt 1),(,,"(r)",lt 1):}`
View SolutionIn elliptical orbit of a planet, as the planet moves from apogee position to perigee position to perigee position, match the following columns
`{:(,"Column-I",,"Column-II"),("(A)","Speed of planet","(p)","Remains same"),("(B)","Distance of planet from centre of sun","(q)","Decreases"),("(C)","Potential energy","(r)","Increase"),("(D)","Angular momentum about centre of sun","(s)","Cannot say"):}`
View SolutionMatch the following columns
`{:(,"Column-I",,"Column-II"),("(A)",underset("satellite in circular orbit")("Time period of an earth"),"(p)","Independent of mass of satellite"),("(B)","Orbital velocity of satellite","(q)","Independent of radius of orbit"),("(C)","Mechanical energy of satellite","(r)","Independent of mass of earth"),(,,"(s)","None"):}`
View SolutionIf earth decreases its rotational speed. Match the following columns
`{:(,"Column-I",,"Column-II"),("(A)","Value of g at pole","(p)","Will remain same"),("(B)","Value of g at equator","(q)","Will increase"),("(C)","Distance of geostationary","(r)","Will decrease"),("(D)","Energy of geostationary satellite","(s)","Cannot say"):}`
View SolutionMatch the following columns. (for a satellite in circular orbit)
`{:(,"Column-I",,"Column-II"),("(A)","Kinetic energy","(p)",-(GMm)/(2r)),("(B)","Potential energy","(q)",sqrt((GM)/(r))),("(C)","Total energy","(r)",-(GMm)/(r)),("(D)","Orbital speed","(s)",(GMm)/(2r)):}`
View Solution
(B) Chapter Exercises questions and complete solutions for chapter GRAVITATION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY NEET Class 11 PHYSICS GRAVITATION
- (A) Chapter Exercises
- (B) Chapter Exercises
- (C) Chapter Exercises
- Check Point 10.1
- Check Point 10.2
- Check Point 10.3
- Check Point 10.4
- Check Point 10.5
- Check Point 10.6
- Example
- Exercise 13.1
- Exercise 13.2
- Exercise 13.3
- Exercise 13.4
- Exercise 13.5
- Exercise 13.6
- Exercise 13.7
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Examples