Complete Solutions to Example of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| DC PANDEY | Example |
| Number Of Questions | 99 |
| Academic Year | 2023-24 |
Three point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View SolutionSix particles each of mass 'm' are placed at six verties A,B,C,D,Eand F of a regular hexagon of side 'a'. A seventh particle of mass 'M' is kept at center 'O' of the hexagon.
(a)Find net force on 'M'.
(b)Find net force on 'M' if particles at A is removed.
(c) Find net force on 'M' if particles at A and C are removed .
View SolutionFive particles each of mass 'm' are kept at five verties of a regular pentagon . A sixth particles of mass 'M' is kept at center of the pentagon 'O'.Distance between'M' and is 'm' is 'a'. Find
(a) net force on 'M'
(b) magnitude of net force on 'M' if any one particle is removed from one of the verties.
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionA uniform ring of mass m is lying at a distance `sqrt(3)` a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
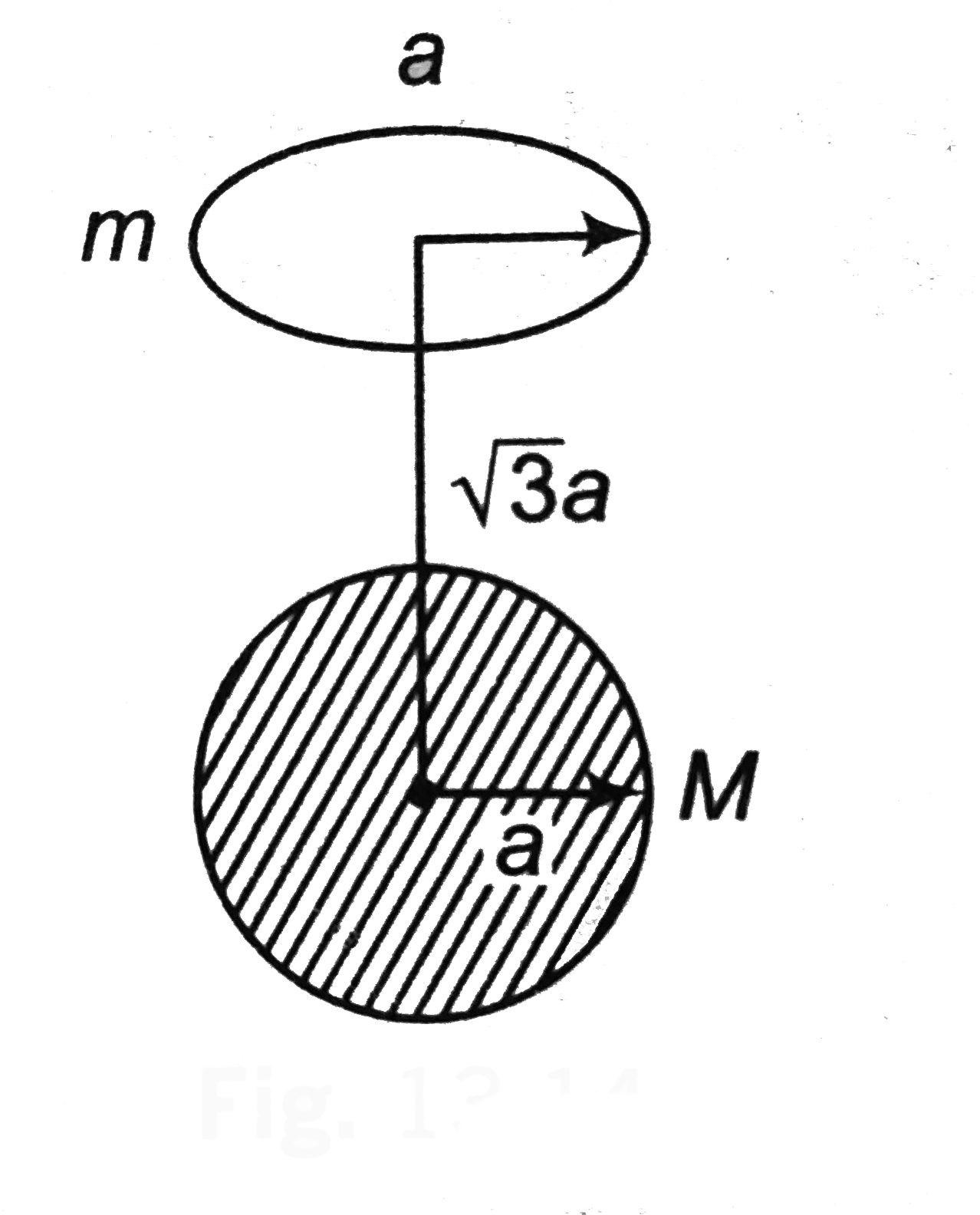
View SolutionAssuming earth to be a sphere of uniform mass density, how much would a body wrigh galf way down the centre of rhe centre of the earth , if it weighed 100 N on the surface?
View SolutionSuppose the earth increases its speed of rotation . At what new time period will the weightof a body on the equator becomes zero? Take `g=10 m/s^2` and radius of the earth `R=6400 km`.
View SolutionDraw g' versus `d and g'` versus `h` graph. Here, 'd' is depth below the surface of earth and `h` is the height from the surface of earth.
View SolutionAt what depth below the surface of earth, value of acceleration due to gravity is same as the value at height `h =R`, where R is the radius of earth.
View SolutionThree point masses 'm' each are kept at three verties of a square pf side 'a' as shown in figure. Find gravitation potential and field strength at point O.
 .
.
View SolutionFour point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
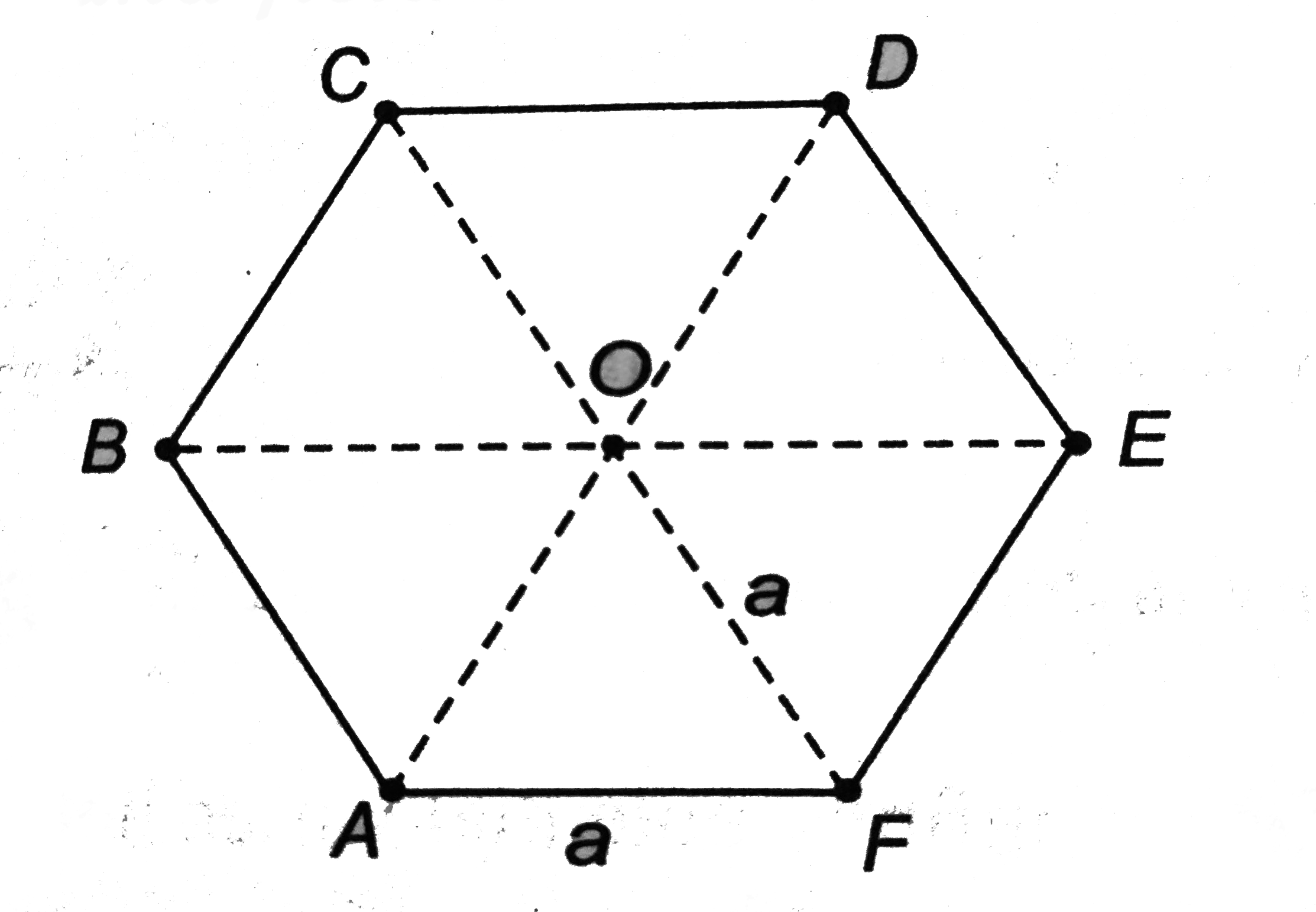 .
.
View SolutionAt what distance 'd' from the surface of a solid sphere of radius 'R',
(a)potential is sme as at a distance `(R)/(2)` from the centre ?
(b) field strengt is ame as at a distance `(R)/(4)` from centre.
View SolutionGravitational potential in `x-y` plan varies with `x` and `y`
coordinates as
`V = x^(2)y+2xy`
Find gravitational field strength `E`.
View SolutionGravtational potential at a distance 'r' from a point mass 'm' is
`V = -(GM)/(r)`
Find gravitational field strength at that point.
View SolutionGravtational potential varies alolngl x-axis as shown in figure .

(a) Plot E versus x graph corresponding to given `V-x` graph.
(b) A mass of 2 kg is kept at `x = 3m`. Find gravitational force on it.
View SolutionGravitational field in `x-y` plane is given as
`E = (2xhati+3Y^(2)hatj)N//kg`
Fin difference in gravitation potential between two points A and B, where
co-ordinates of A and B are `(2m, 4m) and (6m,0)`.
View SolutionThree masses of `1kg`, `2kg`, and `3kg`, are placed at the vertices of an equilateral traingle of side `1m`. Find the gravitational potential energy of this system.
Take `G= 6.67xx10^(-11) N-m^(2)//kg^(2)`.
View SolutionEight particles of mass 'm' each are placed at the verties of a cube of side 'a' . Find gravitational potential energy of this system .
 .
.
View SolutionA particle of mass 'm' is raised from the surface of earth to a height h = 2R. Find work done by some external agent in the process. Here, R is the radius of earth and `g` the acceleration due to gravity on earth's surface.
View SolutionAparticle is projected from the surface of the earth with an intial speed of `4.0 km//s`.Find the maximum height attained by the particle. Radius of earth = 6400km `g = 9.8 m//s^(2)`.
View SolutionCalculate the escape velocity from the moon. The mass of the moon `=7.4xx10^22kg` and radius of the moon `=1740km
View SolutionKinetic energy of a particle on the surface is ` e_(0)` and potential energy is`-E_(0)/(2)`.
(a) Will the particle escape to infinity ?
(b) At some height some height its kinetic energy becomes `0.6 E_(0)`. What is potential energy at this height ?
(c) If the particle escape to infinity , what is kinetic energy of the particle at infinity ?
View SolutionAs orbital radius r of a satellite is increased, state which of the following quantities will increase and which will decrease ?
(i) Orbital speed
(ii) Time period
(iii) Frequence
(iv) Angular speed
(v) Kinetic energy
(vi) Potential energy
(vii) Toyal mechanical energy .
View SolutionA geostationary satellite is orbiting the earth at a height of `6R` above the surface oof earth where R is the radius of the earth .The time period of another satellite at a distance of `3.5R` from the centre of the earth is ….. hours.
View SolutionA spaceship is launced into a circular orbit close to the earth's aurface . What additional velocity has now to be imparted to the spaceship in the orbit to overcome the gravitational pull. Radius of earth `= 6400 km`, `g = 9.8m//s^(2)`.
View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the earth.
(i) Determine the height of the satellite above the earth's surface.
(ii) If the satellite is stopped suddenly in its orbit and allowed to fall freely onto the earth, find the speed with which it hits the surface of the earth.
View SolutionName the physical quantites which remain constant in a planetary motion (in elliptical orbits).
View SolutionConsider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
View SolutionA planet moving around sun sweeps area `A_(1)` in 2 days, `A_(2)` in 3 days and `A_(3)` in 6 days, then find the relation between `A_(1),A_(2) and A_(3)`

View SolutionThe figure shows elliptical orbit of a plant P about the sun S. The shaded area CSD is twice tha shaded area ASB. If `t_(1)` is the time taken by the planet to move from C to D and `t_(2)` is the time to move from A to B, determine the ratio `t_(1)//t_(2)`
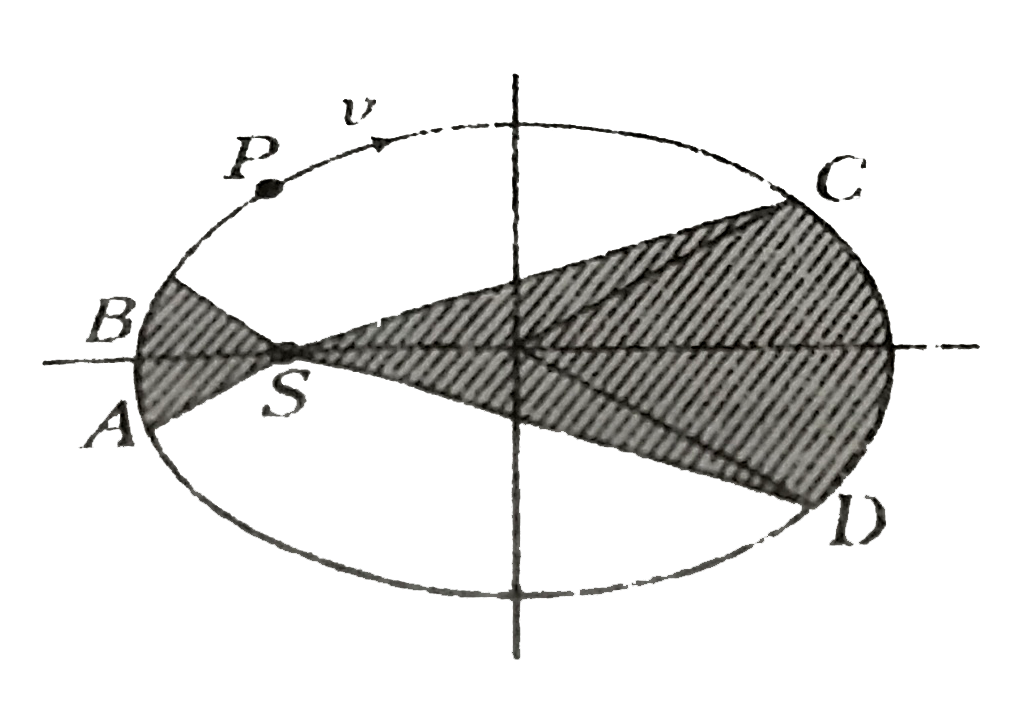
View SolutionA satellite of time period 2A h is orbiting the earth at a height 6R above the surface of earth, where R is radius of earth. What will be the time period of another satellite at a height 2.5 R from the surface of earth ?
View SolutionThe planet neptune travels around the sun with a period of 165 yr. What is the radius of the orbit approximately, if the orbitt is considered as circular ?
View SolutionTwo heavy particles of masses 40 kg and 60 kg attracts each other with a fore of `4 xx 10^(-5) N`. If G is `6xx10^(-11) N-m^(2) kg^(-2)`, calculate the distance between them.
View SolutionIf the distance between the two spherical bodies is increased to four times, then by how many times, the mass of one of the bodies to be changed to maintain the same gravitational force ?
View SolutionTwo particles A and B having masses M and 4M respectively are kept at a distance 2.73 m apart. Another small particle of mass m is to be placed so that the net gravitational force on it is zero. What will be its distance from body A ?
View SolutionSpheres of the same material and same radius `r` are touching each other. Show that gravitational force between them is directly proportional to `r^(4)`.
View SolutionForce between two objects of equal masses is F, If 25 % mass of one object is transferred to the other object, then find the new force.
View Solution(a) A uniform rod of mass `M` and length `L` is placed at distance `L` from a point mass `m` as shown. Find force on `m`
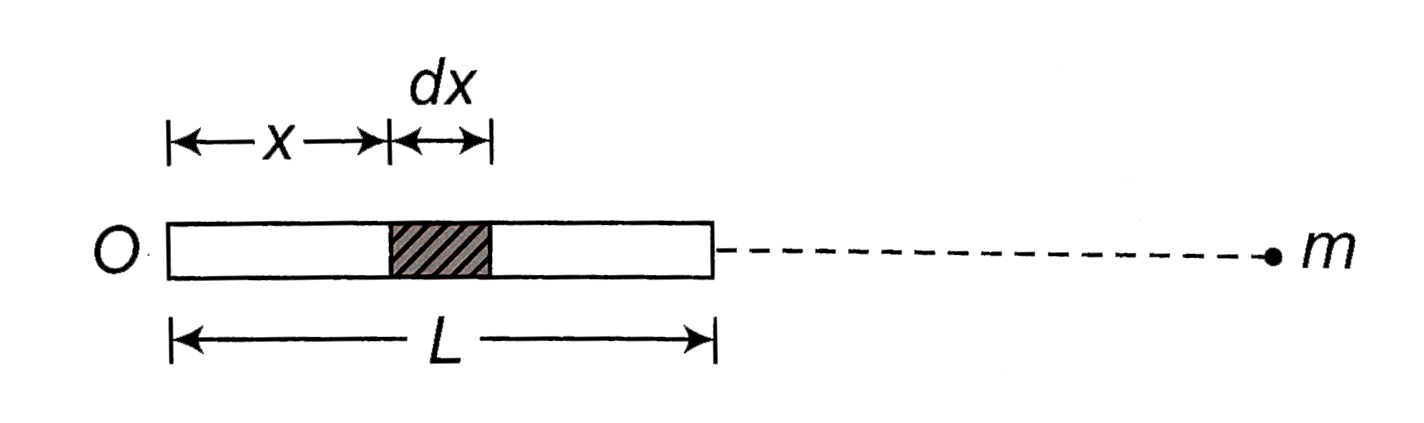
(b) A semiconductor wire has a length `L` and mass `M`. A particle of mass `m` is placed at the centre of the circle. find the gravitational attraction on the particle due to the wire.
View SolutionTwo particles of equal mass `m_(0)` are moving round a circle of radius r due to their mutual gravitational interaction. Find the time period of each particle.
View SolutionThree masses, each equal to M, are placed at the three corners of a square of side a. the force of attraction on unit mass at the fourth corner will be
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral `Delta PQR` and a mass of 2kg is placed at the centroid O of the triangle which is at a distance of `sqrt(2)`m from each the verticles of the triangle. Find the force (in newton) acting on the mass of 2 kg.
View SolutionThe acceleration due to gravity at the moon's surface is `1.67 ms^(-2)`. If the radius of the moon is `1.74 xx 10^(6) m`, calculate the mass of the moon.
View SolutionAssume that if the earth were made of lead of relative density 11.3, then what would be the value of acceleration due to gravity on the earth surface ?
View SolutionWhat will be the relation between the acceleration due to gravity on the surface of the earth and on a planet respectively, whose mass and radius are four times that of the earth ?
View SolutionAt what height above the earth's surface the acceleration due to gravity will be 1/9 th of its value at the earth’s surface? Radius of earth is 6400 km.
View SolutionAt what altitude, the acceleration due to gravity reduces to one fourth of its value as that on the surface of the earth ? Take radius of earth as `6.4 xx 10^(6) m`, g on the surface of the earth as `9.8 ms^(-2)`.
View SolutionAt what height the acceleration due to gravity decreasing by 51 % of its value on the surface of th earth ?
View SolutionAt what depth from the surface of the earth, the acceleration due to gravity will be half the value of g on the surface of the earth ?
View SolutionAt which depth from Earth surface, acceleration due to gravity is decreased by 1 % ?
View SolutionAssuming earth to be a sphere of uniform mass density, how much would a body weigh half way down the centre of the earth, if it weighed 100 N on the surface ?
View SolutionDetermine the decrease in the weight of a body when it is taken 32 km below the earth surface. Take radius of the earth as 6400 km.
View Solutionimagine a new planet having the same density as that of earth but it is 3 times bigger than the earth is size. If the acceleration due to gravity on the surface of earth is g and that on the surface of the new planet is g', then find the relation between g and g'.
View SolutionFind the imaginary angular velocity of the earth for which the effective acceleration due to gravity at the equator shall be zero. (take `g = 10 m//s^(2)` for the acceleration due to gravity, if the earth were at rest and radius of earth equal to 6400 km and `phi = 60^(@)`)
View SolutionCalculate the angular speed of rotation of the Earth so that the apparent g at the equator becomes half of its value at the surface. Also calculate the length of the day in this situation.
View SolutionFind the value of angular velocity of axial rotation of the earth, such that weight of a person at equator becomes 3/4 of its weight at pole, Radius of the earth at equator is 6400 km.
View SolutionSuppose the earth increases it speed of rotation. At what new time period will the weight of a body on the equator becomes zero ? (Take, `g = 10 ms^(-2)` and radius of earth R = 6400 km)
View SolutionTwo point masses of mass 10 kg and 1000 kg are at a distance 1 m apart. At which points on the line joining them, will the gravitational field intensity be zero ?
View SolutionFigure shows a system of point masses placed on X-axis. Find the net gravitational field intensity at the origin

Take sum of an infinite GP as `S = (a)/(1-r)`
where a= first term and r = Least common ratio.
View SolutionTwo solid spheres of radius 10 cm and masses 800 kg and 600 kg, are at a distance 0.25 m apart. Calculate distance 0.20 m from the 800 kg sphere and 0.1 m from the 600 kg sphere and does not lie on the line joining their centres. Given, `G = 6.6 xx 10^(-11) N-m^(2) kg^(-2)`.
View SolutionGravitational field at the surface of a solid sphere is `1.5 xx 10^(-4) "N kg"^(-1)`. Find the gravitational field at a point situated inside the sphere at a distance equal to half of rhe radius of the solid sphere.
View SolutionTwo concentric spherical shells have masses `m_(1) and m_(2)` and radii `r_(1) and r_(2) (r_(2) gt r_(1))`. What is the force exerted by this system on a particle of mass `m_(3)`. If it is placed at a distance `r(r_(1) lt r lt r_(2))` from the centre ?
View SolutionMass of 20 kg is distributed uniformly over a ring of radius 2m. Find the the grvitational field at a point lies an th axis of the ring at a distance of `2 sqrt(3)` m from the centre.
View SolutionA heavy point of mass 15 kg is placed at the origin of coordinate axis. Find the gravitational potential at a point located at `x=5 cm` on X-axis.
View SolutionTwo heavy point masses of mass `10^(3)` kg and `10^(5)` kg are separated by a distance of 200 m. What will be the potential at the mid-point of the line joining them ?
View SolutionThe radius of the earth is `6.37 xx 10^(6)` m and its mean density is `5.5 xx 10^(3) "kg m"^(-3)` and `G = 6.67 xx 10^(-11) "N-m"^(2) kg^(-2)` Find the gravitational potential on the surface of the earth.
View SolutionAt a point above the surface of the earth, the gravitational potential is `-5.12 xx 10^(7)` J/kg and the acceleration due to gravity is `6.4 m//s^(2)`. Assuming the mean radius of the earth to be 6400 km, calculate the height of the point above the earth's surface.
View SolutionA particle of mass 1 kg is kept on the surface of a uniform thin spherical shell of mass 20 kg and radius 1 m. Find the work to be done against the gravitational force between them to take the particle away from the thin spherical shell.
View SolutionA particle of mass M is placed at the centre of a spherical shell of same mass and radius a. What will be the magnitude of the gravitational potential at a point situated at a/2 distance from the centre ?
View SolutionMass of 10 kg is distributed uniformly over a ring of radius 1m. Find the gravitational potential at a point lies on the axis of the ring at a distance of 1m from the centre.
View SolutionIf gravitational potential is `V = xy^(2)`, find the gravitational field at `(2,1)`
View SolutionIf gravitational field is given by `E -x hat(i) - 2 y^(2) hat(j)`. When gravitational potential is zero ar (0,0) find potential cat (2,1)
View SolutionTwo point masses 1 kg and 4 kg are separated by a distance of 10 cm. Find gravitational potential energy of the two point masses.
View SolutionThree masses of 1 kg, 2kg, and 3 kg are placed at the vertices of an equilateral triangle of side 1m. Find the gravitational potential energy of this system
(Take, `G = 6.67 xx 10^(-11) "N-m"^(-2)kg^(-2)`)
View SolutionThree particle each of mass m are placed at the corners of an equilateral at the corners of an equilateral triangle of side d as shown in figure. Calculate (a) the potential energy of the system, (b) work done on this system if the side of the traingle is changed from d to 2d.

View SolutionInfinite number of bodies, each of mass 2kg are situated on X-axis at distance `1m,2m,4m,8m,` respectively from the origin, What is the resulting gravitational potential due to this system at the origin ?
View SolutionThe mass of the earth is `6 xx 10^(24) kg`. The constant of gravitation `G = 6.67 xx 10^(-11) "N-m"^(-2) kg^(-2)`. The potential energy of the earth and moon system is `-7.79 xx 10^(28) J`. Determine the mean distance between earth and moon.
View SolutionA body of mass `m` is raised to a height 10 R from the surface of the earth, where R is the radius of the earth. Find the increase in potential energy. (G = universal constant of gravitational, M = mass of the earth and g= acceleration due to gravity)
View SolutionFind the change in the gravitational potential energy when a body of mass `m` is raised to a height nR above the surface of the earth. (Here, R is the radius of the earth)
View SolutionAn object is dropped from height `h=2 R` on the surface of earth. Find the speed with which it will collide with ground by neglecting effect of air. (Where R is radius of earth, take mass of earth M)
View SolutionFind the binding energy of a satellite of mass `m` in orbit of radius `r`, (R = radius of earth, g = acceleration due to gravity)
View SolutionCalculate the escape velocity from the surface of a planet of mass `14.8 xx 10^(22)` kg. It is given that radius of the planet is `3.48 xx 10^(6)` m.
View SolutionThe ratio of the masses and radii of two planets are `4:6 and 8:18`. What is the ratio of the escape speed at their surface ?
View SolutionJupiter has a mass 318 times that of earth, and its radius is 11.2 times the earth's radius Estimate the escape velocity of a body from Jupiter's surface, given that the escape velocity from the earth's surface `11.2 kms^(-1)`.
View SolutionAt what temperature, hydrogen molecules will escape from the earth's surface ? (Take, radius of earth `R_(e)=6.4xx10^(6)m`, mass of hydrogen molecule `m=0.34 xx 10^(-26)`kg, Boltzmann constant `k=1.38xx10^(-23)JK^(-1)` and acceleration due to gravity `= 9.8 xx ms^(-2)`) also take rms speed of gas as `v_(rms) = sqrt((3kT)/(m))`.
View SolutionA space-ship is launched into a circular orbit close to the Earth,s surface. What additional speed should now be imparted to the spaceship so that it overcome the gravitational pull of the Earth.
Take kinetic energy of the space-ship,
K = total energy of space-ship `= (GMm)/(2R)`
where m = mass of space-ship, M= mass of the earth and R = radius of the earth.
View Solution_S01_013_Q01.png)
A very small groove is made in the earth, and a particle of mass `m_(0)` is placed at `(R)/(2)` distance from the centre. Find the escape speed of the particle for that place.
View SolutionThe earth is assumed to be a sphere of raduis `R`. A plateform is arranged at a height `R` from the surface of the `fv_(e)`, where `v_(e)` is its escape velocity form the surface of the earth. The value of `f` is
View SolutionA body is projected upwards with a velocity of `4 xx 11.2 "km s"^(-1)` from the surface of earth.What will be the velocity of the body when it escapes from the gravitational pull of earth ?
View SolutionA particle is projected from the surface of earth with intial speed of 4 km/s. Find the maximum height attained by the particle. Radius of earth = 6400 km and `g = 9.8 m//s^(2)`
View SolutionA particle is projected vertically upwards the surface of the earth (radius `R_(e))` with a speed equal to one fourth of escape velocity what is the maximum height attained by it from the surface of the earth?
View SolutionWith what velocity must a body be thrown from earth's surface so that it may reach a maximum height of `4R_(e)` above the Earth's surface ? (Radius of the Earth `R_(e)=6400 km,g=9.8 ms^(-2)`).
View SolutionA satellite circled around the earth at a distance of 100 km. Determine its orbital velocity, if the radius of the earth is 6400 km and `g = 9.8 ms^(-2)`.
View SolutionA satellite is launched into a circular orbit close to the earth's surface. What additional velocity has new to be imparted to the satellite in the orbit to overcome the gravitational pull ?
View SolutionA satellite revolves around the earth at a height of 1000 km. The radius of the earth is `6.38 xx 10^(3)`km. Mass of the earth is `6xx10^(24)kg and G=6.67xx10^(-14)"N-m"^(2)kg^(-2)`. Determine its orbital velocity and period of revolution.
View SolutionA satellite contructs a circle around the earth in 90 minutes. Determine the height of the satellite above the earth's surface.
View SolutionIf a spaceship orbits the earth at a height of 500 km from its surface, then determine its (i) kinetic energy, (ii) potential energy, and (iii) total energy (iv) binding energy. Mass of the satellite = 300 kg, Mass of the earth `= 6xx10^(24) kg`, radius of the earth `= 6.4 xx 10^(6) m, G=6.67 xx 10^(-11) "N-m"^(2) kg^(-2)`. Will your answer alter if the earth were to shrink suddenly to half its size ?
View SolutionWhat will be the mass of an astronaut in a space satellite if at earth's surface the astronaut weighs 250 N ? (Take `g = 10 ms^(-2)`)
View Solution
Example questions and complete solutions for chapter GRAVITATION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS GRAVITATION
- (A) Chapter Exercises
- (B) Chapter Exercises
- (C) Chapter Exercises
- Check Point 10.1
- Check Point 10.2
- Check Point 10.3
- Check Point 10.4
- Check Point 10.5
- Check Point 10.6
- Example
- Exercise 13.1
- Exercise 13.2
- Exercise 13.3
- Exercise 13.4
- Exercise 13.5
- Exercise 13.6
- Exercise 13.7
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Examples