Complete Solutions to Level 2 Single Correct of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| DC PANDEY | Level 2 Single Correct |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
An artifical satellite of mass `m` is moving in a circular orbit at a height equal to the radius `R` of the earth. Suddenly due to intensity explosion the satellite breakes into two parts of equal pieces. One part of the satellite stops just after the explosion. The increase in the mechanical energy of the system due to explosion will be
(Given, acceleration due to gravity on the surface of earth is g)04:18View SolutionA semicircular wire hs a length L and mass M. A paricle of mass m is placed at the centre of the circle. Find the gravitational attraction on the particle due to the wire.
08:30View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
04:08View SolutionA projectile is fired from the surface of earth of radius `R` with a velocity `k upsilon_(e)` (where `upsilon_(e)` is the escape velocity from surface of earth and `k lt 1)`. Neglecting air resistance, the maximum height of rise from centre of earth is
03:53View SolutionSuppose a verticle tunnel is dug along the diametal of earth , which is assumed to be a sphere of unifrom mass density `rho`. If a body of mass `m` is throws in this tunal, its acceleration at a distance `y` from the centre is given by
 03:17View Solution
03:17View SolutionA train of mass `m` moves with a velocity `upsilon` on the equator from east to west. If `omega` is the angular speed of earth about its axis and `R` is the radius of the earth then the normal reaction acting on the train is
02:33View SolutionThe figure represents a solid uniform sphere of mass `M` and radius `R`. A spherical cavity of radius `r` is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 08:20View Solution
08:20View SolutionIf `upsilon_(e)` is the escape velocity for earth when a projectile is fired from the surface of earth. Then, the escape velocity if the same projectile is fired from its centre is
03:09View SolutionIf the gravitational field intensity at a point is given by `g = (GM)/(r^(2.5))`. Then, the potential at a distance `r` is
02:08View SolutionThree identical particles each of mass `M` move along a common circlar path of radius `R` under the mutual interaction of each other. The velocity of each particle is
05:35View SolutionIf `T` be the period of revolution of a plant revolving around sun in an orbit of mean radius `R`, then identify the incorrect graph.
01:28View SolutionA person brings a mass of `1 kg` from infinty to a point `A`. Initially, the mass was at rest but it moves at a speed of `3 m//s` as it reaches `A`. The work done by the person on the mass is `- 5.5 J`. The gravitational potential at `A` is
02:21View SolutionWith what minmum speed should `m` be projected from point `C` in presence of two fixed masses `M` each at `A` and `B` as shows in the figure such that mass `m` should escape the gravitational of `A` and `B` ?
02:41View SolutionConsider two configurations of a system of three particles of masses `m`, `2m` and `3m`. The work done by gravity in changing the configuration of the system from figure (i) to figure (ii) is
 05:09View Solution
05:09View SolutionA tuning is dug along the diameter of the earth. There is particle of mass `m` at the centre of the tunel. Find the minimum velocity given to the particle so that is just reaches to the surface of the earth. `(R =` radius of earth)
06:26View SolutionA body is projected horizontally from the surface of the earth (radius `= R`) with a velocity equal to `n` times the escape velocity. Neglect rotational effect of the earth. The maximum height attained by the body from the earth `s` surface is `R//2`. Then, `n` must be
04:53View SolutionA tunnel is dug in the earth across one of its diameter. Two masses `m` and `2m` are dropped from the two ends of the tunel. The masses collide and stick each other. They perform `SHM`, the ampulitude of which is `(R =` radius of earth)
05:22View SolutionThere are two planets. The ratio of radius of two planets is `k` but radio of acceleration due to gravity of both planets is g. What will be the ratio of their escape velocity ?
01:43View SolutionA body of mass `2 kg` is moving under the influence of a central force whose potential energy is given by `U = 2r^(3) J`. If the body is moving in a circular orbit of `5 m`, its energy will be
02:18View SolutionA research satellite of mass `200 kg` circles the earth in an orbit of average radius `3 R//2`, where `R` is the radius of the earth. Assuming the gravitational pull on the mass of `1 kg` on the earth's surface to be `10 N`, the pull (in Newton) on the satellite will be
03:12View SolutionA satellite of mass `m` revolves around the earth of radius `R` at a height `x` from its surface. If `g` is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
02:11View SolutionA solid sphere of uniform density and radius `R` applies a gravitational force attraction equal to `F_(1)` on a particle placed at `P`, distance `2R` from the centre `O` of the sphere. A spherical cavity of radius `R//2` is now made in the sphere as shows in figure. The particle with cavity now applies a gravitational force `F_(2)` on same particle placed at `P`. The radio `F_(2)//F_(1)` will be
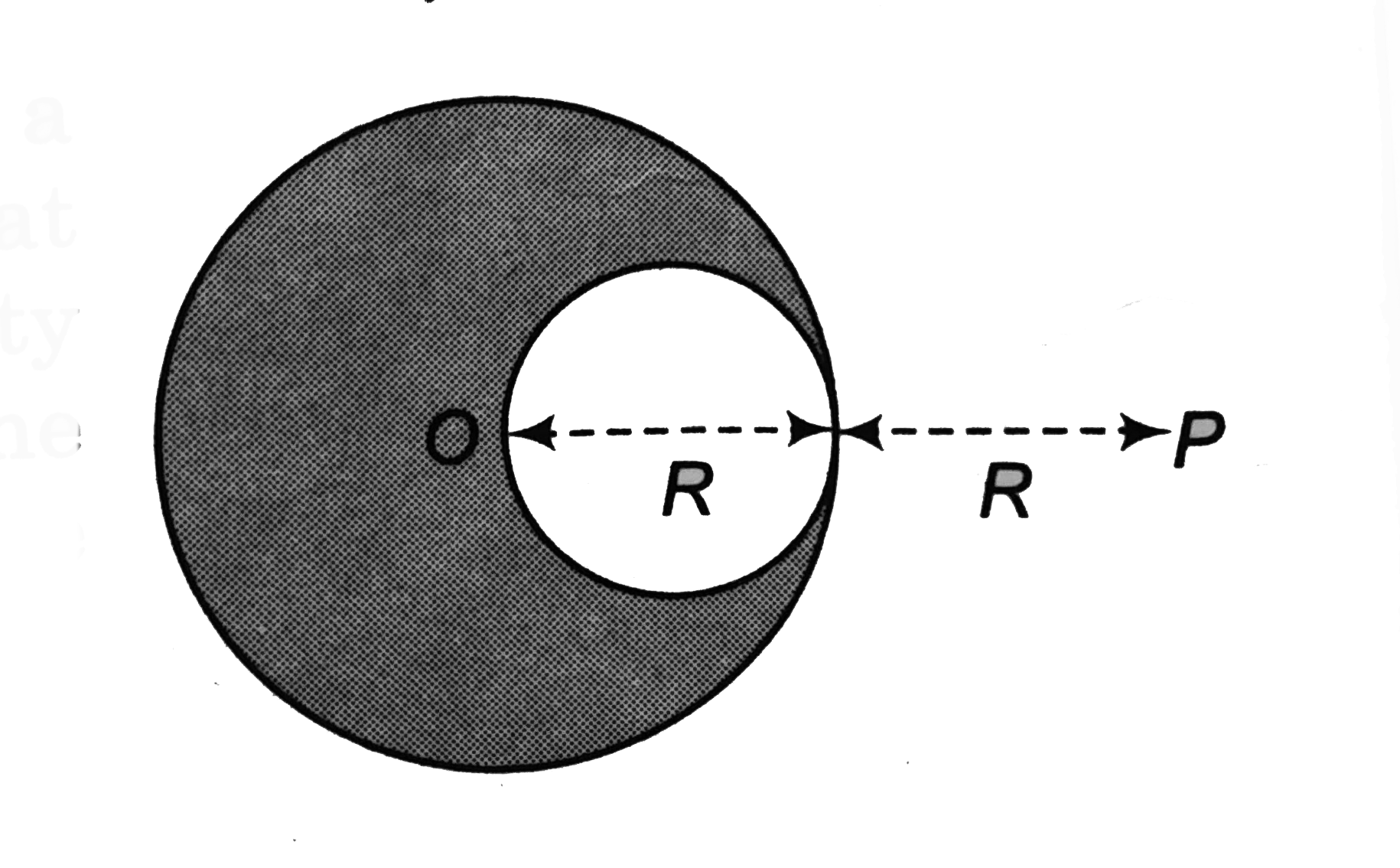 05:41View Solution
05:41View Solution
Level 2 Single Correct questions and complete solutions for chapter GRAVITATION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS GRAVITATION
- (A) Chapter Exercises
- (B) Chapter Exercises
- (C) Chapter Exercises
- Check Point 10.1
- Check Point 10.2
- Check Point 10.3
- Check Point 10.4
- Check Point 10.5
- Check Point 10.6
- Example
- Exercise 13.1
- Exercise 13.2
- Exercise 13.3
- Exercise 13.4
- Exercise 13.5
- Exercise 13.6
- Exercise 13.7
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Examples
