Complete Solutions to SCQ_TYPE of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| DC PANDEY MASTER PROBLEM PACKAGE | SCQ_TYPE |
| Number Of Questions | 41 |
| Academic Year | 2023-24 |
A ball is hit by a batsman at an angle of `37^(@)` as shown in figure. The man standing at `P` should run at what minimum velocity so that he catches the ball before it strikes the ground. Assume that height of man is negligible in comparison to maximum height of projectile.

View SolutionA particle is projected from the ground with an initial velocity of `20m//s` at an angle of `30^(@)` with horizontal. The magnitude of change in velocity in a time interval from `t=0` to `t=0.5s` is (`g=10m//s^(2)`)
View SolutionA particle is pojected from the ground at an angle of `theta` with the horizontal with an initial speed of `u`. Time after which velocity vector of the projectile is perpendicular to the initial velocity is
View SolutionIn projectile motion, the modulus of rate of change of speed
View SolutionA particle of mass `m` is projected from the ground with initial linear momentum `p` (magnitude) such that to have maximum possible range, its minimum kinetic energy will be
View SolutionA particle is projected with initial velocity of `hati+2hatj`. The eqaution of trajectory is `(take g=10ms^(-2))`
View SolutionA particle is projected from the ground with an initial speed of v at an angle `theta` with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
View SolutionA particle `A` is projected verically upwards. Another indentical particle `B` is projected at an angle of `45^(@)`. Both reach the same height. The ratio of the initial kinetic energy of `A` to that of `B` is `-`
View SolutionRatio of minimum kinetic energies of two projectiles of same mass is `4:1`. The ratio of the maximum height attained by them is also `4:1` . The ratio of their ranges would be
View SolutionA particle is projected from gound At a height of 0.4 m from the ground, the velocity of a projective in vector form is `vecv=(6hati+2hatj)m//s` (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is `(g=10m//s^(2))`
View SolutionThe horizontal range and miximum height attained by a projectile are `R and H`, respectively. If a constant horizontal acceleration `a = g//4` is imparted to the projectile due to wind, then its horizontal range and maximum height will be
View SolutionA particle is projected at an angle of `60^(@)` above the horizontal with a speed of `10m//s`. After some time the direction of its velocity makes an angle of `30^(@)` above the horizontal. The speed of the particle at this instant is s
View SolutionThe trajectory of a projectile in a vertical plane is `y = ax - bx^2`, where `a and b` are constant and `x and y` are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.
View SolutionA stone is projected from ground. Its path is a shown in figure. At which point its speed is decreasing at fastest rate?

View SolutionA projectile strikes the inclined plane perpendicularly as shown in the figure. Which of the following statements is correct?
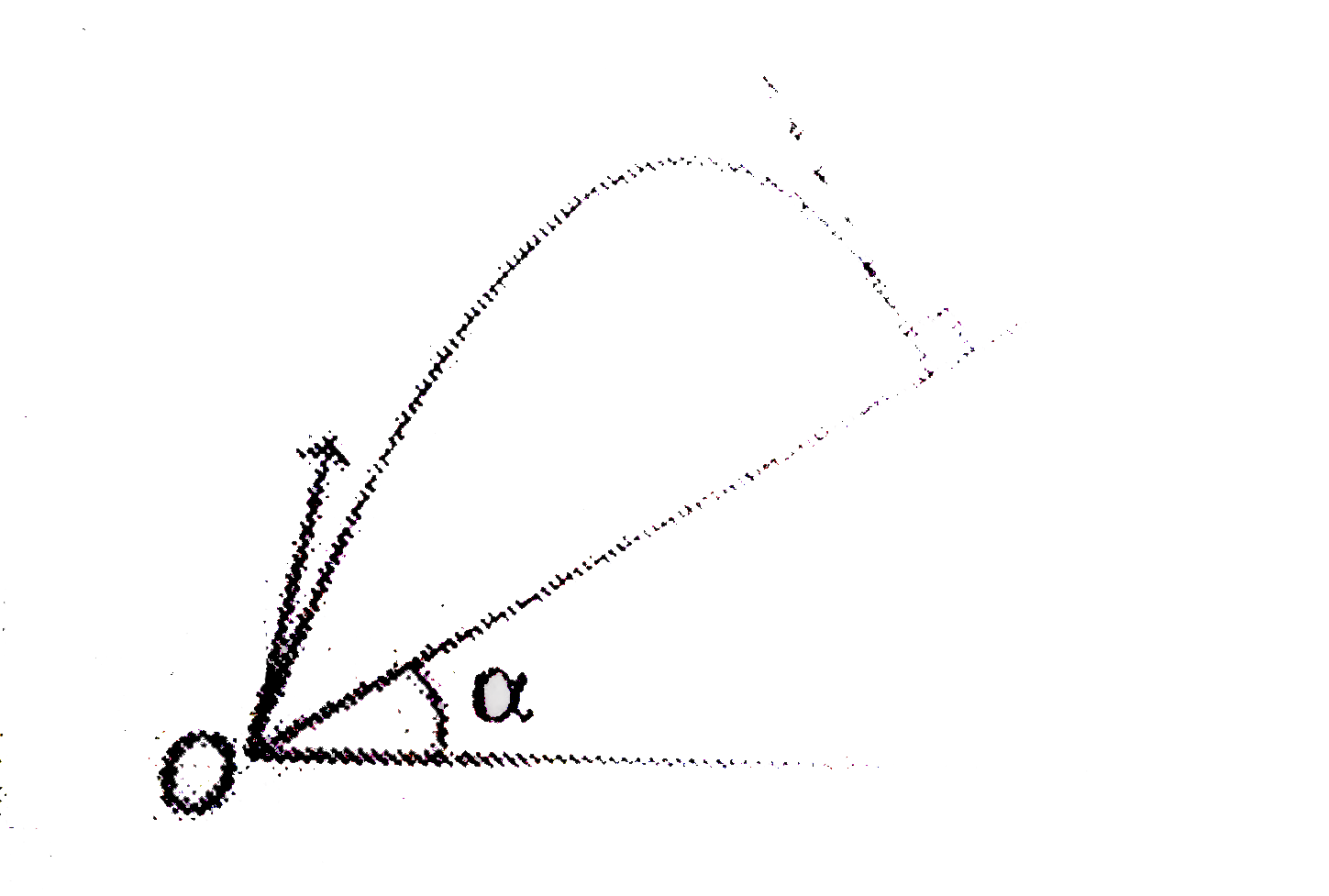
View SolutionThe direction of projection of particle is shown in the figure for an observer on trolley. An observer on the ground sees the ball rising vertically. The maximum height reached by the ball as seen from the trolley is

View SolutionA body is projected at an angle of `45^(@)` with horizontal from a point on ground at distance `6m` from the foot of a vertical pole. It just crosses the top of the pole and falls on ground on the other side at a distance of `3m` from the foot of the pole. The height of the pole is:
View SolutionA projectile is thrown with velocity `u` making an angle `theta` with the horizontal. Its time of flight on the horizontal ground is 4 second. The projectile is moving at angle of `45^(@)` with the horizontal just one second after the projection. Hence the angle `theta` is (take `g=10m//s^(2)`)
View SolutionAir is blowing and is providing a constant horizontal acceleration `a_(x)=g` to the particle as shown in the figure. Particle is projected from point `P` with a velocity `u` in upward direction. Let `Q` be the highest point of the particle. Speed of the particle at highest point `Q` is

View SolutionA very broad elevator is going up vertically with a constant acceleration of `2m//s^(2)`. At the instant when its velocity is `4m//s`, a ball is projected from the floor of the lift wht as of `4m//s` relative to the floor at an elevation of `30^(@)`. The time taken by the ball to return the floor is `(g=10m//s^(2))`
View SolutionA particle is projected up an inclined plane with initial speed `v=20m//s` at an angle `theta=30^(@)` with plane. The component of its velocity perpendicular to plane when it strikes the plane is
View SolutionTwo particle are projected from the same point on ground simultaneously with speed `20m//s` and `20//sqrt(3)m//s` at angle `30^(@)` and `60^(@)` with the horizontal in the same direction. The maximum distance between them till both of them strikes the ground is approximately `(g=10m//s^(2))`
View SolutionTwo particles A and B projected simultaneously from a point situated on a horizontal place. The particle A is projected vertically up with a velcity `v_(A)` while the particle B is projected up at an angle `30^(@)` with horizontal with velocity `v_(B)`. After 5s the particles were observed moving mutually perpendicular to each other. The velocity of projection of the particle `v_(A) and v_(B)` respectively are:
View SolutionA projectile is fired at an angle of `30^(@)` to the horizontal such that the vertical component of its initial velocity is `80m//s`. Its time of fight is `T`. Its velocity at `t=T//4` has a magnitude of nearly.
View SolutionA particle starts from the origin of co-ordinates at time `t=0` and moves in the`xy` plane with a constant acceleration `alpha` in the `y`-direction. Its equation of motion is `y=betax^(2)`. Its velocity component in the `x`-direction
View SolutionThe speed of a projectile when it is at its greatest height is `sqrt(2//5)` times its speed at half the maximum height. The angle of projection is
View SolutionAfter one second the velocity of a projectile makes an angle of `45^(@)` with the horizontal. After another one more second its is travelling horizontally. The magnitude of its initial velocity and angle of projectile are
`(g=10m//s^(2))`
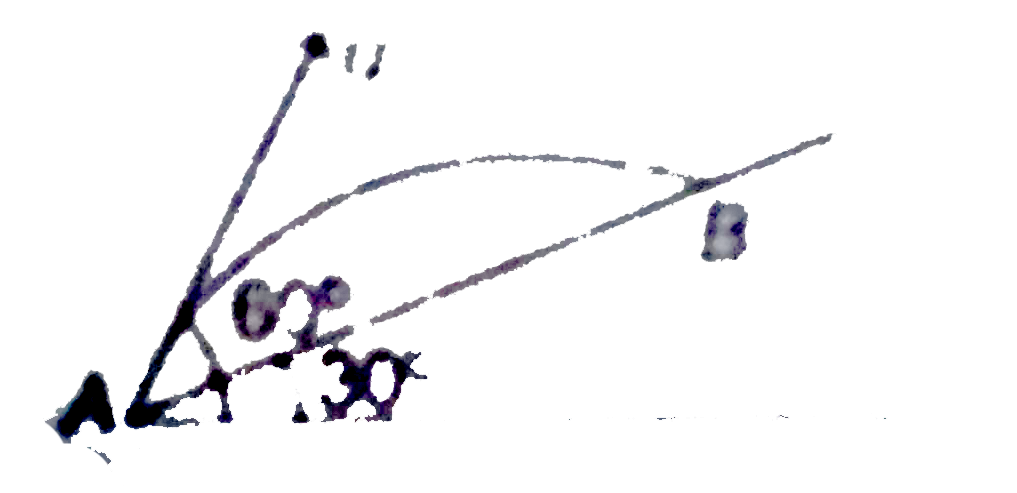
View SolutionA particle is projected with a certain velocity at an angle `alpha` above the horizontal from the foot of an inclined plane of inclination `30^(@)`. If the particle strikes the plane normally then `alpha` is equal to
View SolutionTime taken by the particle to reach from `A` to `B` is `t`. Then the distance `AB` is equal to
View SolutionA projectile of mass `2kg` has velocities `3m//s` and `4m/s` at two points during its flight in the uniform gravitational field of the earth. If these two velocities are perpendicular to each other, then the minimum kinetic enerty of the particle during its flight is
View SolutionWith what minimum speed must a particle be projected from origin so that it is able to pass through a given point `(30m, 40m)` ? Take `g=10m//s^(2)`
View SolutionA particle is projected from a point `A` with velocity `sqrt(2)u` an angle of `45^(@)` with horizontal as shown in figure. It strikes the plane `BC` at right angles. The velocity of the particle at the time of collision is

View SolutionA projectile is thrown with a velocity of `10sqrt(2)m//s` at an angle of `45^(@)` with horizontal. The interval between the moments when speed is `sqrt(125)m//s` is `(g=10m//s^(2))`
View SolutionA large rectangular box moves vertically downward with an acceleration `a`. A toy gun fixed at `A` and aimed towards `C` fires a particle `P`.

View SolutionTwo particles projected vertically upward from points `(0,0)` and `(1,0)m` with uniform velocity `10m//s` and `vm//s` respectively, as shown in the figure. It is found that they collide after time `t` in space. Time `t` is `1/(5(sqrt(x)-1))`. Calculate `x`
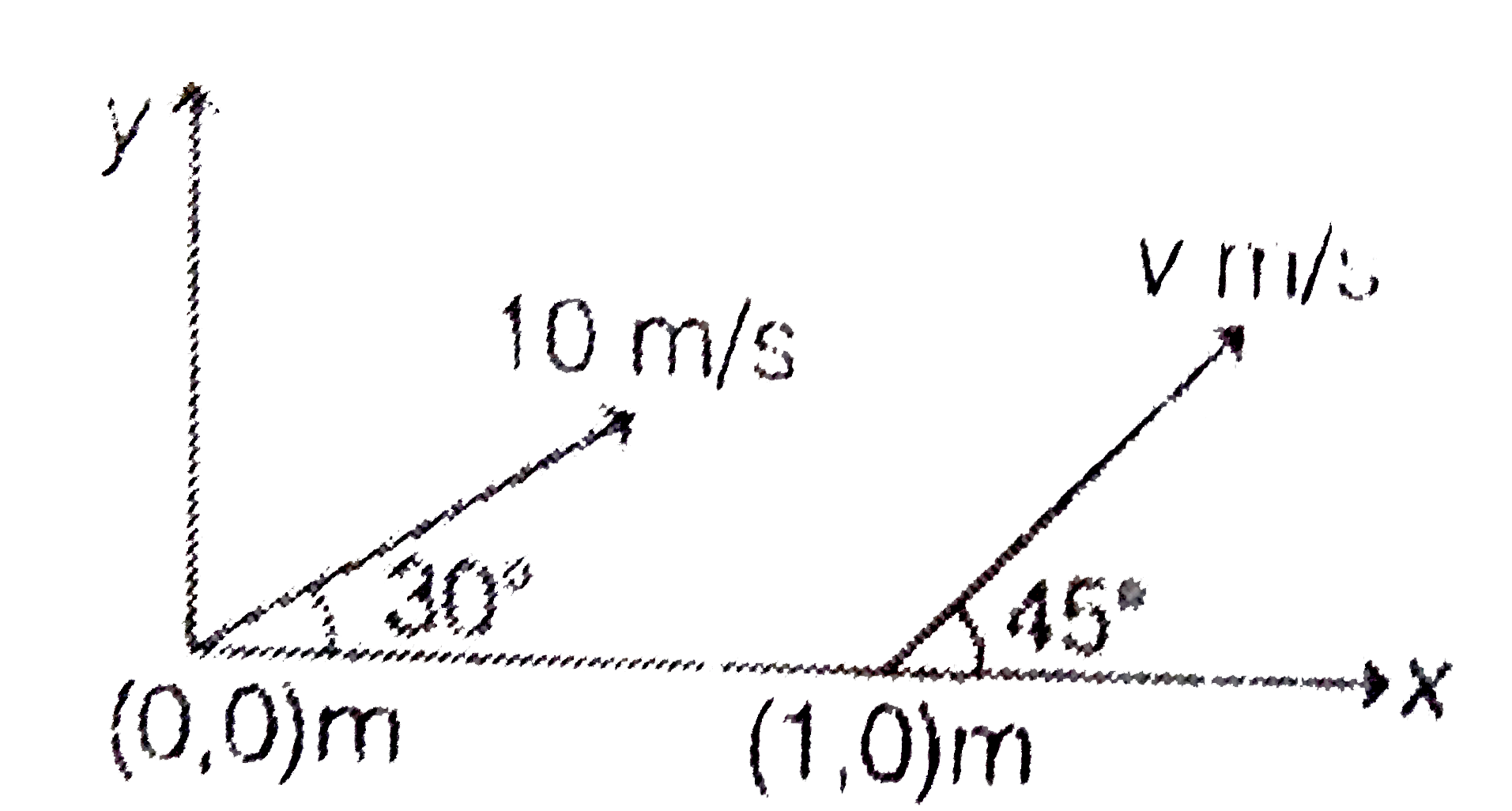
View SolutionTrajectory of two particles projected from origin with speeds `v_(1)` and `v_(2)` at angles `theta_(1)` and `theta_(2)` with positive `x`- axis respectively are as shown in the figure. Given that `(g=-10m//s^(2)(hatj))`. Choose the correct option related to diagram.

View SolutionTwo inclined planes `OA` and `OB` of inclinations `alpha` and `beta` equal to `30^(@)` are as shown in the figure. A particle is projected at an angle of `90^(@)` with plane `OA` from point `A` and it strikes the plane `OB` at point `B` normally. Then find the speed of projection `u` in m/s.
(Given that `OA=OB=20cm` and `g=10m//s^(2)`)

View SolutionAn elavator is going up vertically with a constant accelerartion of `2m//s^(2)`. At the instant when its velocity is `4m//s` a ball is projected from the floor of the elavator with a speed of `4m//s` relative to the floor with an angular eleavation of `60^(@)`. The time taken by the ball to return the floor is `(g=10m//s^(2))`
View SolutionFigure shows a cube of side length `'a'` placed on a horizontal surface. A particle projected from `A` with speed `u`, at an angle `theta=tan^(-1)sqrt(5)` with horizontal, just touches the cube at two vertices as shown. Find projection speed `u`.
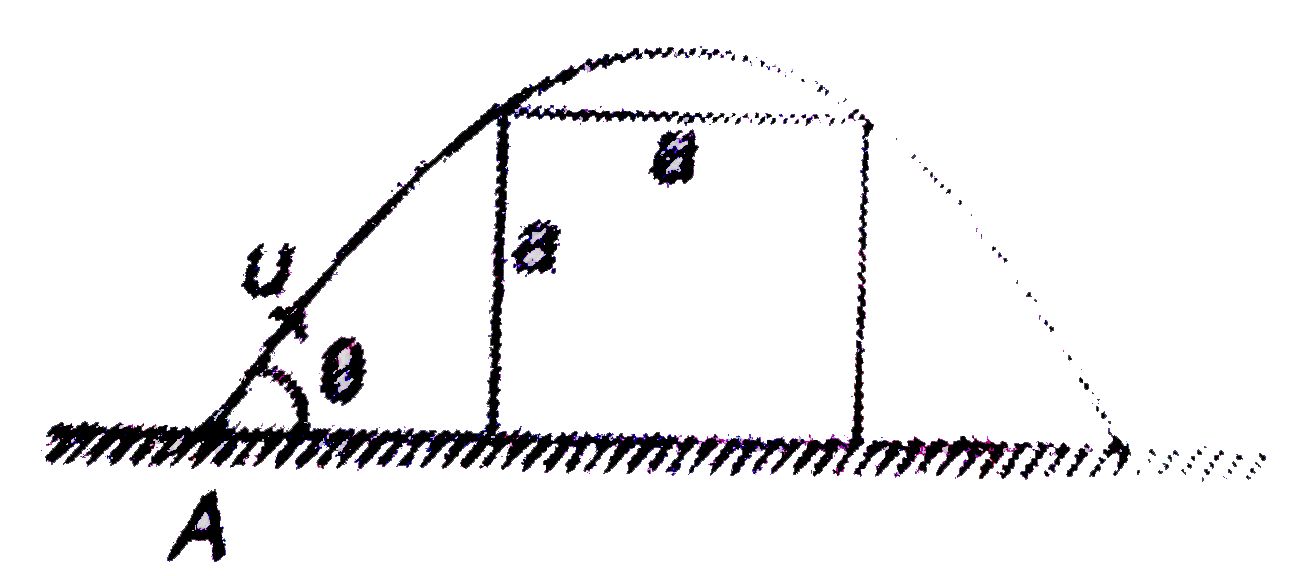
View SolutionTwo particles are projected simultaneously from two different points in a uniform gravitational field and collide with each other at a point `Q(2b,3b)`. In the absence of the field they would have collided at `P(2b,8b)` in a time `t_(0)`. The acceleration due to gravity at this place `g` must be equal to
View SolutionTwo children are playing a game in which they try to hit a small box using a spring loaded machine gun, which is fixed rigidly to a table at a height `h` above the top of the box. The spring has spring constant `k` and the box is at a horizontal distance `l` from `O`. The first child compresses the spring a distanc `x_(0)` and find that the marble falls short of box by a horizontal distance `y`. The second child compreses the spring by an extra amount `Deltax` so that marble lands in the box. The value of `Deltax` is
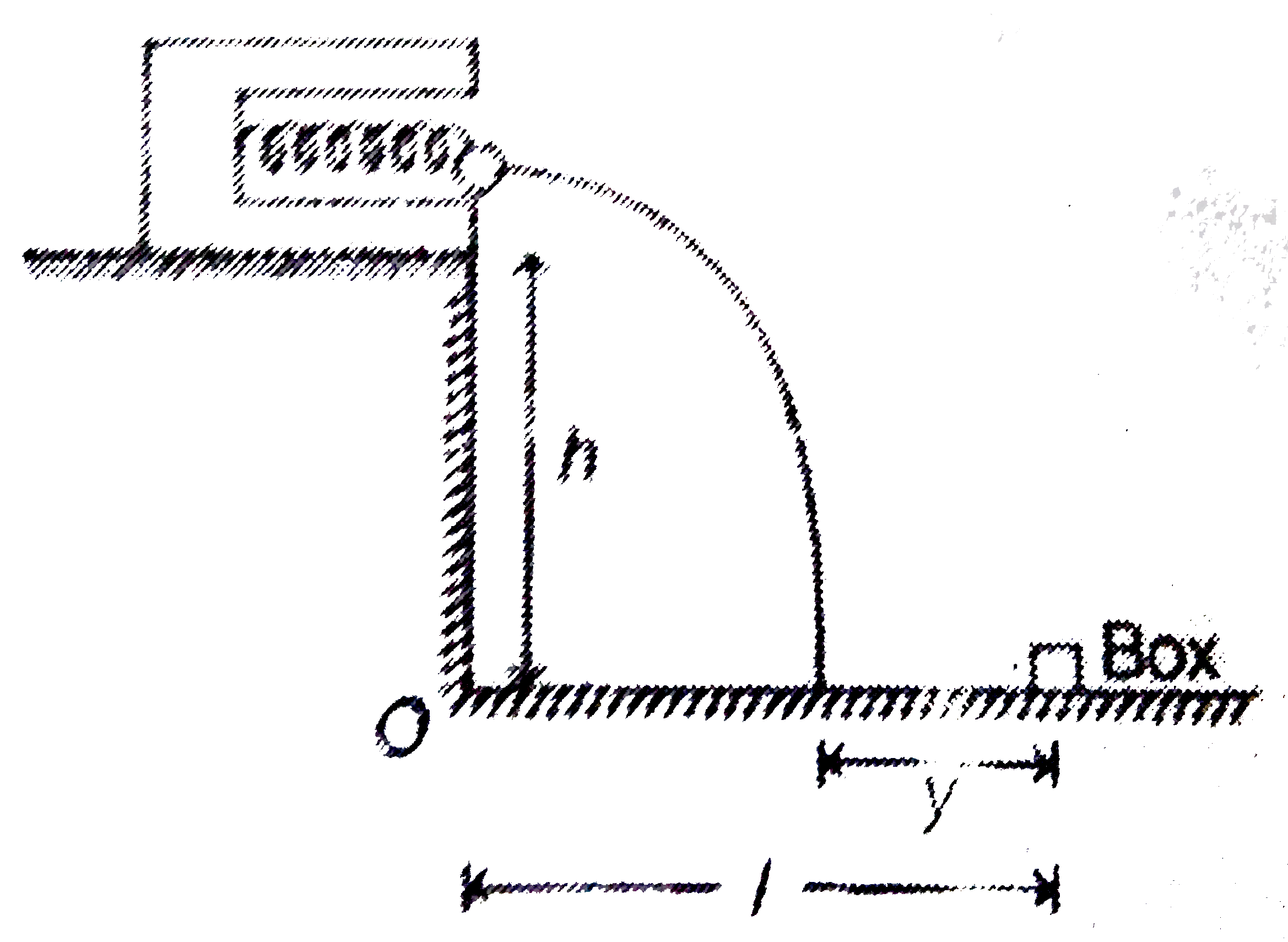
View Solution
SCQ_TYPE questions and complete solutions for chapter KINEMATICS of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY MASTER PROBLEM PACKAGE Class 11 PHYSICS KINEMATICS
- Assertion And Reason
- Comprehension
- COMPREHENSION_TYPE
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Exercise 6.1
- Exercise 6.2
- Exercise 6.3
- Exercise 6.4
- Exercise 6.5
- Exercise 6.6
- Exercise 6.7
- Exercise 6.8
- Exercise 6.9
- INTEGER_TYPE
- MATCH THE COLUMN
- MCQ_TYPE
- Miscellaneous Example
- More Than One Correct
- Objective
- SCQ_TYPE
- Subjective
- Subjective Questions