Complete Solutions to Objective of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| DC PANDEY | Objective |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
A stone is released from a rising balloon accelerating upward with acceleration a. The acceleration of the stone just after the release is
01:48View SolutionA ball is thrown vertically upwards from the ground. If `T_1` and `T_2` are the respective time taken in going up and coming down, and the air resistance is not ignored, then
05:20View SolutionThe length of a seconds hand in watch is `1 cm.` The change in velocity of its tip in `15 s` is
04:21View SolutionWhen a ball is thrown up vertically with velocity `v_0`, it reaches a maximum height of h. If one wishes to triple the maximum height then the ball should be thrown with velocity
02:18View SolutionDuring the first `18 min` of a `60 min` trip, a car has an average speed of `11 ms^-1.` What should be the average speed for remaining `42 min` so that car is having an average speed of `21 ms^-1` for the entire trip?
03:26View SolutionA particle moves along a straight line. Its position at any instant is given by `x = 32t-(8t^3)/3` where x is in metres and t in seconds. Find the acceleration of the particle at the instant when particle is at rest.
03:14View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity `v_0`. The distance travelled by the particle in time t will be
06:34View SolutionWater drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. `(g = 10 ms^-2)`
06:13View SolutionA stone is dropped from the top of a tower and one second later, a second stone is thrown vertically downward with a velocity `20 ms^-1`. The second stone will overtake the first after travelling a distance of `(g=10 ms^-2)`
07:42View SolutionA particle moves in the x-y plane with velocity `v_x = 8t-2 and v_y = 2.` If it passes through the point `x =14 and y = 4 at t = 2 s,` the equation of the path is
05:32View SolutionThe horizontal and vertical displacements of a particle moving along a curved line are given by `x=5t and y = 2t^2 + t.` Time after which its velocity vector makes an angle of `45^@` with the horizontal is
03:43View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in `T/3` second?
04:01View SolutionAn ant is at a corner of a cubical room of side a. The ant can move with a constant speed u. The minimum time taken to reach the farthest corner of the cube is
10:58View SolutionA lift starts from rest. Its acceleration is plotted against time. When it comes to rest its height above its starting point is
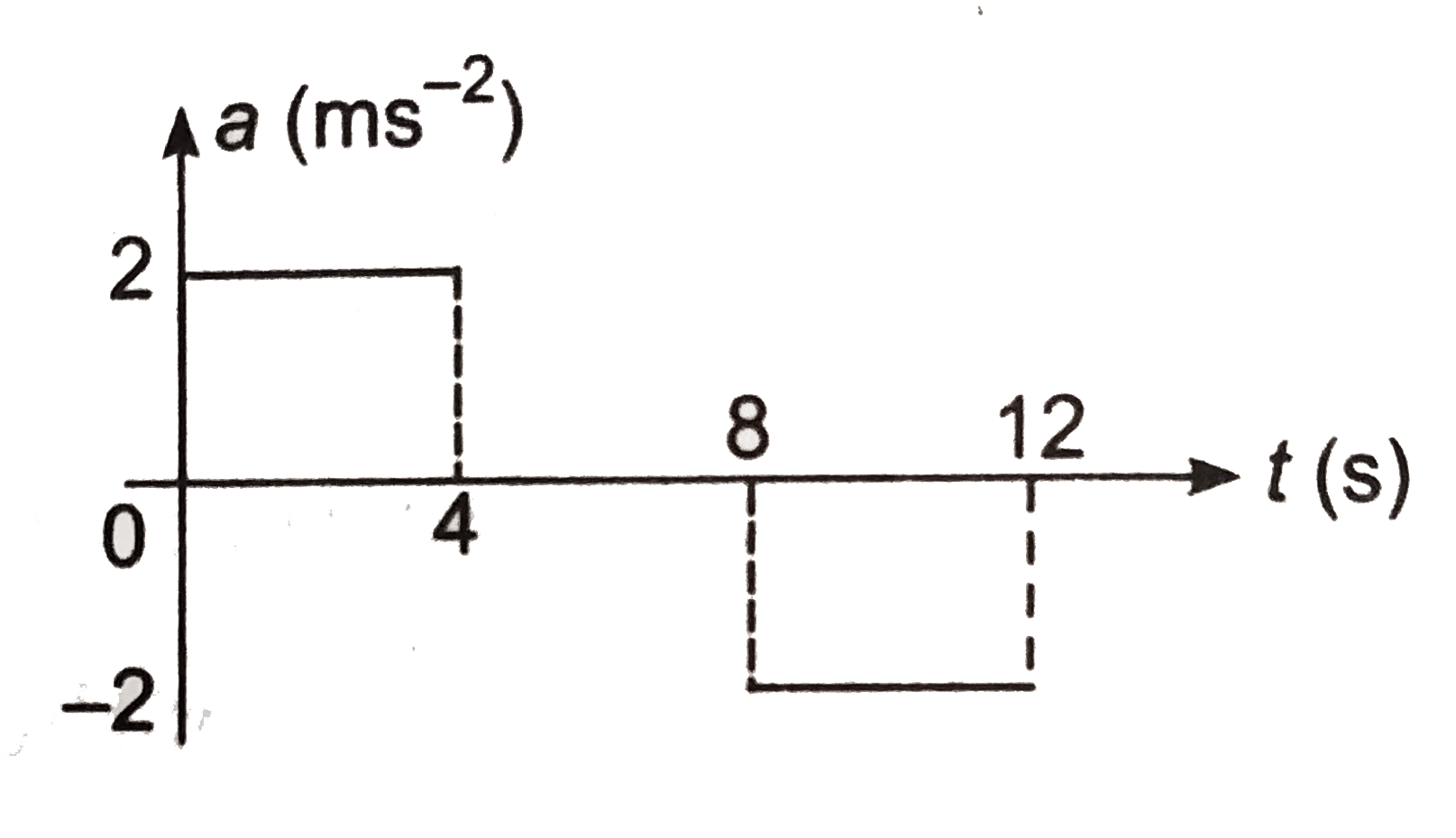 06:29View Solution
06:29View SolutionA lift performs the first part of its ascent with uniform acceleration a and the remaining with uniform retardation `2a.` If t is the time of ascent, find the depth of the shaft.
08:20View SolutionTwo objects are moving along the same straight line. They cross a point A With an acceleration a, 2a and velocity 2u, u at time `t = 0.` The distance moved by the object when one overtakes the
05:42View SolutionA cart is moving horizontally along a straight line with constant speed `30 ms^-1.` A particle is to be fired vertically upwards from the moving cart in such a way that it returns to the cart at the same point from where it was projected after the cart has moved `80 m.` At what speed (relative to the cart) must the projectile be fired? (Take `g = 10 ms^-2`)
04:34View SolutionThe figure shows velocity-time graph of a particle moving along a straight line. Identify the correct statement.
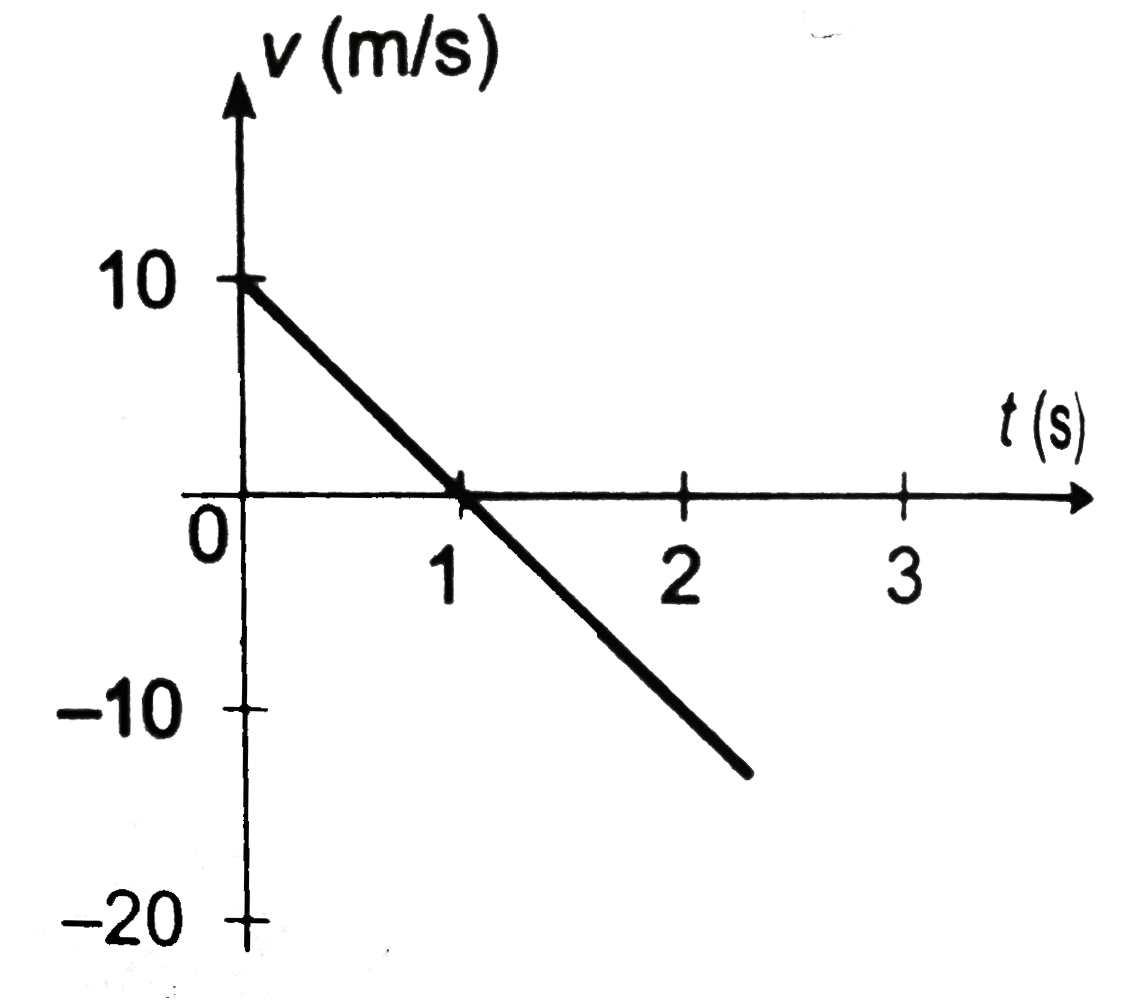 05:05View Solution
05:05View SolutionA ball is thrown vertically upwards from the ground and a student gazing out of the window sees it moving upward past him at `10ms^-1.` The window is at 15 m above the ground level. The velocity of ball 3 s after it was projected from the ground is [Take `g= 10 ms^-2`]
02:27View SolutionA body starts moving with a velocity `v_0 = 10 ms^-1.` It experiences a retardation equal to `0.2v^2.` Its velocity after 2s is given by
02:43View SolutionTwo trains are moving with velocities `v_1 = 10 ms^-1 and v_2 = 20 ms^-1` on the same track in opposite directions. After the application of brakes if their retarding rates are `a_1 = 2 ms^-2 and a_2 = 1 ms^-2` respectively, then the minimum distance of separation between the trains to avoid collision is
04:20View SolutionTwo balls of equal masses are thrown upwards, along the same vertical direction at an interval of 2 seconds, with the same initial velocity of `40m//s`. Then these collide at a height of (Take `g=10m//s^(2)`).
03:30View SolutionA particle is projected vertically upwards and reaches the maximum height H in time T. The height of the partlcle at any time `t (lt T)` will be
02:55View SolutionA particle moves along the curve `y = x^2 /2.` Here x varies with time as `x = t^2 /2.` Where x and y are measured in metres and t in seconds. At `t = 2 s,` the velocity of the particle (in `ms^-1`) is
03:47View SolutionIf the displacement of a particle varies with time as `sqrt x = t+ 3`
01:50View SolutionThe graph describes an airplane's acceleration during its take-off run. The airplane's velocity when it lifts of at `t = 20 s` is
 03:38View Solution
03:38View SolutionA particle moving in a straight line has velocity-displacement equation as `v = 5 sqrt(1 + s).` Here v is in `ms^-1` and s in metres. Select the correct alternative.
02:55View SolutionA particle is thrown upwards from ground. It experiences a constant resistance force which can produce a retardation of `2 ms^-2.` The ratio of time of ascent to time of descent 13 (`g = 10 ms^-2`)
07:59View SolutionA body of mass 10 kg is being acted upon by a force `3t^2` and an opposing constant force of 32 N. The initial speed is `10 ms^-1.`The velocity of body after 5 s is
04:26View SolutionA stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is `10 ms^-1` , then the maximum height attained by the stone is (`g= 10 ms^(-2)`)
03:02View Solution(a) What does `|(dv)/(dt)|` and `(d|v|)/(dt)` represent? (b) Can these be equal?
05:20View SolutionThe coordinates of a particle moving in x-y plane at any time t are `(2 t, t^2).` Find (a) the trajectory of the particle, (b) velocity of particle at time t and (c) acceleration of particle at any time t.
03:14View SolutionA farmer has to go 500 m due north, 400 m due east and 200 m due south to reach his field. If he takes 20 min to reach the field.
(a) What distance he has to walk to reach the field ?
(b) What is the displacement from his house to the field ?
(c) What is the average speed of farmer during the walk ?
(d) What is the average velocity of farmer during the walk ?07:17View SolutionA rocket is fired vertically up from the ground with a resultant vertical acceleration of `10 m//s^2.` The fuel is finished in 1 min and it continues to move up. (a) What is the maximum height reached? (b) Afte2r how much time from then will the maximum height be reached?(Take `g= 10 m//s^2`)
07:16View SolutionA particle is projected upwards from the roof of a tower 60 m high with velocity `20 m//s.` Find
(a) the average speed and
(b) average velocity of the particle upto an instant when it strikes the ground. Take `g= 10 m//s^2`08:08View SolutionA block moves in a straight line with velocity v for time `t_0.` Then, its velocity becomes 2v for next `t_0` time. Finally, its velocity becomes 3v for time T. If average velocity during the complete journey was 2. 5 v, then find T in terms of `t_0.`
02:54View SolutionA particle starting from rest has a constant acceleration of `4 m//s^2` for 4 s. It then retards uniformly for next 8 s and comes to rest. Find during the motion of particle (a) average acceleration (b) average speed and (c) average velocity.
07:18View SolutionA particle moves in a circle of radius `R = 21/22 m` with constant speed `1 m//s.` Find,
(a) magnitude of average velocity and
(b) magnitude of average acceleration in 2 s.06:21View SolutionTwo particles A and B start moving simultaneously along the line joining them in the same direction with acceleration of `1 m//s^2 and 2 m//s^2` and speeds `3 m//s and 1 m//s` respectively. Initially, A is 10 m behind B. What is the minimum distance between them?
06:47View SolutionTwo diamonds begin a free fall from rest from the same height, 1.0 s apart. How long after the first diamond begins to fall will the two diamonds be 10 m apart? Take `g = 10 m//s^2.`
04:28View SolutionTwo bodies are projected vertically upwards from one point with the same initial velocity `v_0.` The second body is projected `t_0 s` after the first. How long after will the bodies meet?
06:08View SolutionDisplacement-time graph of a particle moving in a straight line is as shown in figure.

(a) Find the sign of velocity in regions oa,ab, bc and cd.
(b) Find the sign of acceleration in the above region.07:44View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. In the time interval from `t = 0` to `t = 14 s,` find
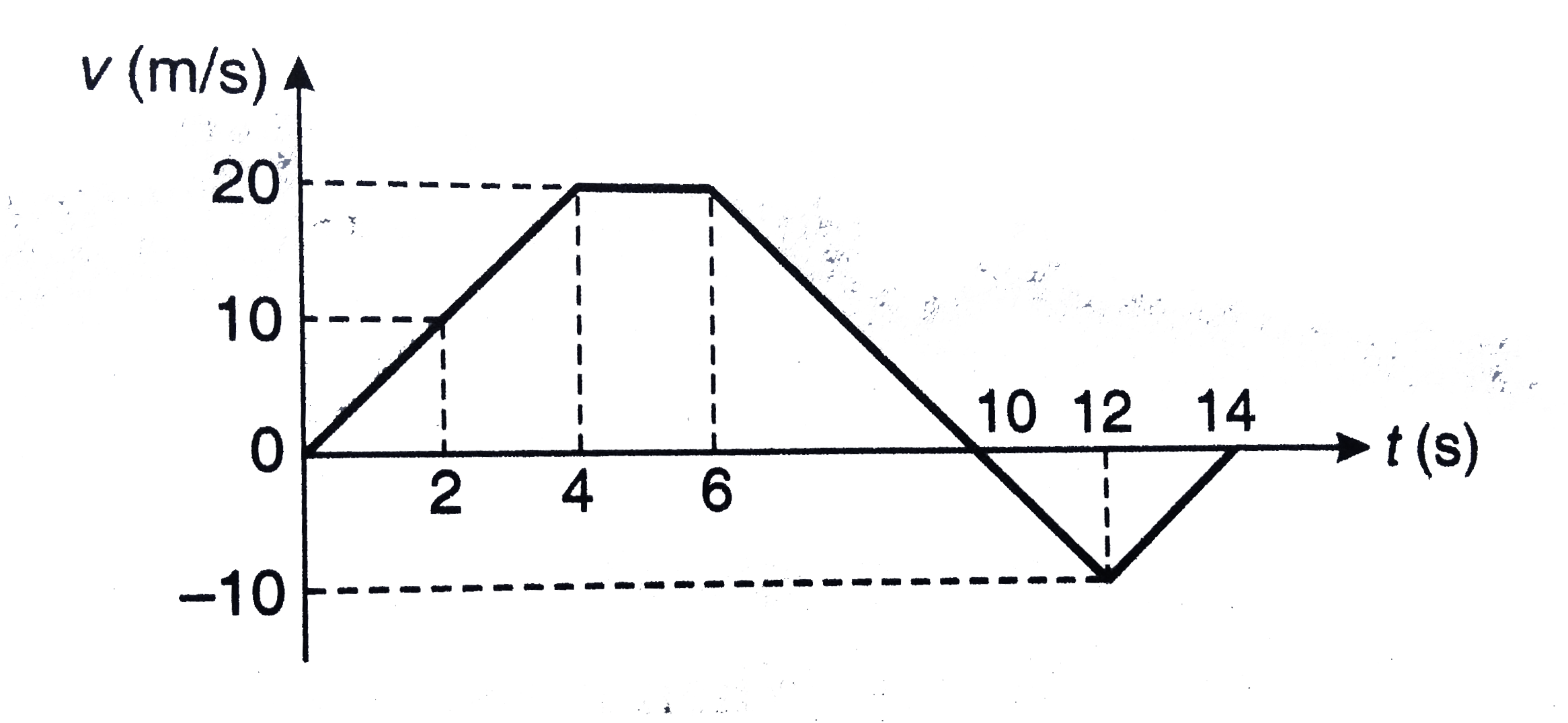
(a) average velocity and
(b) average speed of the particle.05:59View SolutionA person walks up a stalled 15 m long escalator in 90 s. When standing on the same escalator, now moving, the person is carried up in 60 s. How much time would it take that person to walk up the moving escalator? Does the answer depend on the length of the escalator?
04:10View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time `t = t_1 and t = t_2.`
 03:25View Solution
03:25View Solution
Objective questions and complete solutions for chapter KINEMATICS of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS KINEMATICS
- Assertion And Reason
- Comprehension
- COMPREHENSION_TYPE
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Exercise 6.1
- Exercise 6.2
- Exercise 6.3
- Exercise 6.4
- Exercise 6.5
- Exercise 6.6
- Exercise 6.7
- Exercise 6.8
- Exercise 6.9
- INTEGER_TYPE
- MATCH THE COLUMN
- MCQ_TYPE
- Miscellaneous Example
- More Than One Correct
- Objective
- SCQ_TYPE
- Subjective
- Subjective Questions
