Trajectory of two particles projected from origin with speeds v1 and v2 at angles θ1 and θ2 with positive x- axis respectively are as shown in the figure. Given that (g=−10m/s2(ˆj)). Choose the correct option related to diagram.

v1−v2=2v1
θ2−θ1=2θ1
3(v1−v2)=v1
3(θ2−θ1)=θ1
The correct Answer is:D
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - MCQ_TYPE
23 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - COMPREHENSION_TYPE
13 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Subjective Questions
24 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Two particles of equal mass 'm' are projected from the ground with speed v1 and v2 at angles θ1 and θ2 at the same times as shown in figure. The centre of mass of the two particles.

View SolutionTwo particles of equal mass in are projected from the ground with speeds v1 and v2 at angles θ1, and θ2 as shown in the figure. Given θ2>θ1 and v1cosθ1=v2cosθ2Which statement/s is/are correct?
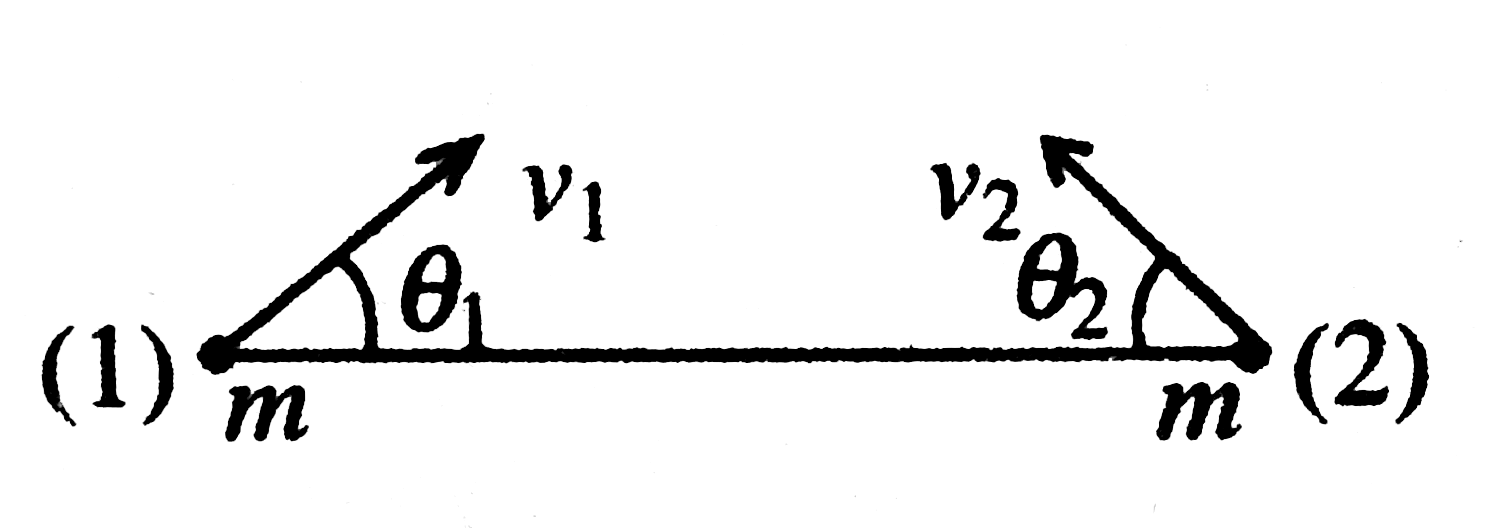
View Solution
Knowledge Check
Two particles of equal mass 'm' are projected from the ground with speed v1 and v2 at angles θ1 and θ2 at the same times as shown in figure. The centre of mass of the two particles.
 Awill move in a vertical line if v1tanθ=v2tanθ2Bwill move in a vertical line if v1sinθ=v2sinθ2Cwill move In a vertical line if v1cotθ1=v2cotθ2Dwill move in a vertical line if v1cosθ1=v2cosθ2
Awill move in a vertical line if v1tanθ=v2tanθ2Bwill move in a vertical line if v1sinθ=v2sinθ2Cwill move In a vertical line if v1cotθ1=v2cotθ2Dwill move in a vertical line if v1cosθ1=v2cosθ2Two particles of equal mass in are projected from the ground with speeds v1 and v2 at angles θ1, and θ2 as shown in the figure. Given θ2>θ1 and v1cosθ1=v2cosθ2Which statement/s is/are correct?
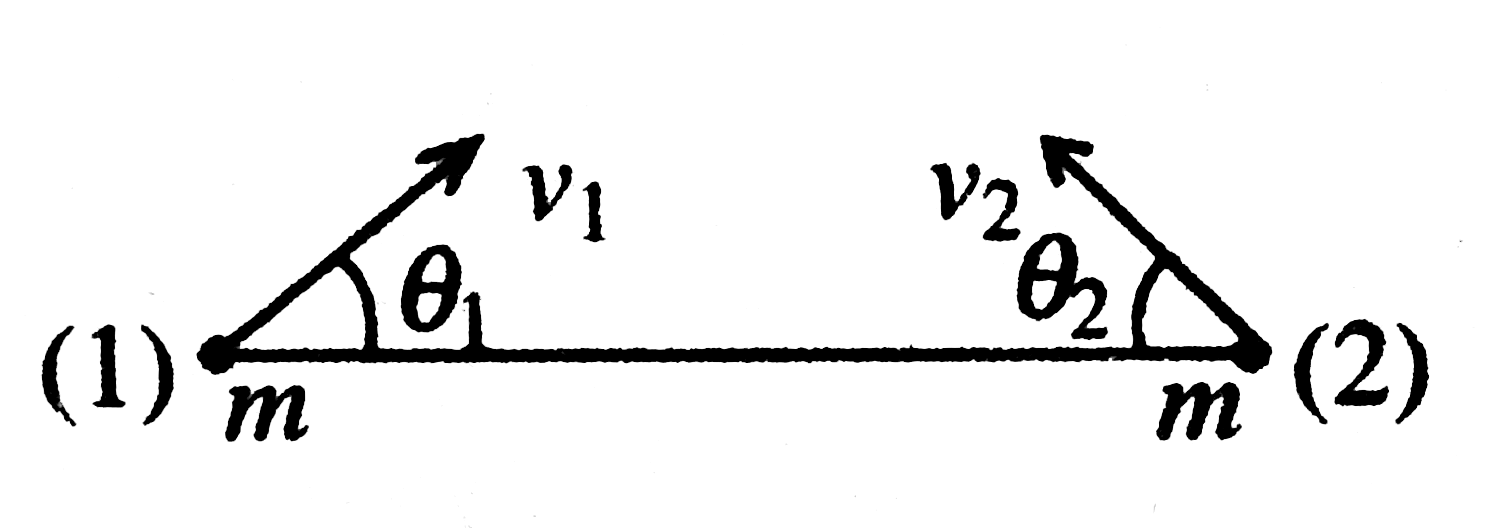 ACentre of mass of particles will move along a vertical line.BCentre of mass of particles will move along a line inclined at some angle with vertical.CParticle '1' will be above vertical. centre of mass level when both particles are in air.DParticle '2' will be above centre of mass level both particles are in air.
ACentre of mass of particles will move along a vertical line.BCentre of mass of particles will move along a line inclined at some angle with vertical.CParticle '1' will be above vertical. centre of mass level when both particles are in air.DParticle '2' will be above centre of mass level both particles are in air.Two particles are projected in air with speed v0 at angles θ1 and θ2 (both acute) to the horizontal,respectively.If the height reached by the first particle greater than that of the second,then thick the right choices
Aangle of projection:θ1>θ2Btime of flight:T2>T1Chorizontal range:R1>R2Dtotal energy : U1>U2
Two particles are projected in air with speed v0 at angles θ1 and θ2 (both acute) to the horizontal,respectively.If the height reached by the first particle greater than that of the second,then thick the right choices
View SolutionTwo particles are projected at the same instant with speeds v1 and v2 making angles α and β with the horizontal as shown in the figure. Nelecting air resistance, the trajectory of the mass center the two particles

View SolutionTwo particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
 .
.
View SolutionTwo particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
 .
.
View SolutionTwo particles are projected at the same instant with speeds v1 and v2 making angles α and β with the horizontal as shown in the figure. Nelecting air resistance, the trajectory of the mass center the two particles

View Solution
