Complete Solutions to PHYSICS of chapter KINETIC THEORY OF GASES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES |
| DISHA | PHYSICS |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
`4.0 g` of a gas occupies `22.4` litres at NTP. The specific heat capacity of the gas at constant volume is `5.0 JK^(-1)mol^(-1)`. If the speed of sound in this gas at NTP is `952 ms^(-1)`. Then the heat capacity at constant pressure is
View SolutionA fixed mass of gas at constant pressure occupies a volume V. The gas undergoes a rise in temperature so that the root mean square velocity of its molecules is doubled. The new volume will be
View SolutionA gaseous mixture consists of 16g of helium and 16 g of oxygen. The ratio `(C_p)/(C_v)` of the mixture is
View SolutionAir is pumped into an automobile tyre's tube up to pressure of `200kPa` in the morning when the air temperature is `20^(@)C.` During the day the temperature rises to `40^(@)C` and the tube expand by `2%`. Calculate the pressure of the air in the tube at this temperature.
View SolutionCalculate the rms speed of smoke particles of mass `5 xx 10^(-17) kg` in their Brownian motion in air at NTP. Given `k_(B) = 1.38 xx 10^(-23) J//K`
View SolutionOne mole of an ideal gas requires 207J heat to raise the temperature by 10 K, when heated at constant pressure. If the same gas is heated at constant volume to raise the temperature by 10 K, then heat required is [given gas constant. R = 8.3 1/(mol -K)]
View SolutionFigure shows the variation in temperature (DT) with the amount of heat supplied (Q) in an isobaric process corresponding to a monoatomic (M), diatomic (D) and a polyatomic (P) gas. The initial state of all the gases are the same and the scales for the two axes coincide. Ignoring vibrational degrees of freedom, the lines a, b and c respectively correspond to
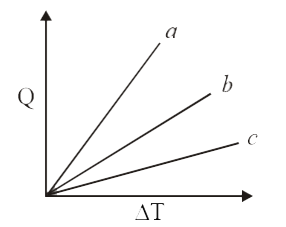
View Solution1 mole of a monatomic and 2 mole of a diatomic gas are mixed. The resulting gas is taken through a process in which molar heat capacity was found 3R. Polytropic constant in the process is
View SolutionThe density of a gas is `6xx 10^(-2 )kg//m^(3)` and the root mean square velocity of the gas molecules is 500 m/s. The pressure exerted by the gas on the walls of the vessel is
View SolutionThe absolute temperature of the gas is increased 3 times. What will be the increases in root mean square velocity of the gas molecules?
View SolutionConsider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increase as `V^q`, where V is the volume of the gas. The value of q is : `(gamma=(C_p)/(C_v))`
View SolutionOne kg of a diatomic gas is at pressure of `8xx10^4N//m^2`. The density of the gas is `4kg//m^3`. What is the energy of the gas due to its thermal motion?
View SolutionA thermally insulated vessel contains an ideal gas of molecular mass M and ratio of specific heats `gamma`. It is moving with speed v and it's suddenly brought to rest. Assuming no heat is lost to the surroundings, Its temperature increases by:
View SolutionFigure shows a parabolic graph between T and 1/V for a mixture of a gases undergoing an adiabatic process. What is the ratio of `V_(nms)` of molecules and speed of sound in mixture?
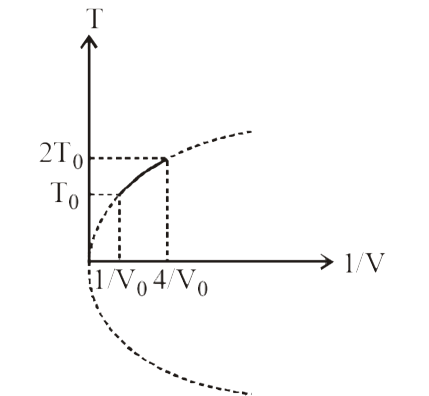
View SolutionThe work of 146 kJ is performed in order to compress one kilo mole of a gas adiabatically and in this process the temperature of the gas increases by `7^@C`. The gas is `(R=8.3ml^-1Jmol^-1K^-1)`
View SolutionAt what temperature is the root mean square velocity of gaseous hydrogen molecules is equal to that of oxygen molecules at `47^(@)C`?
View SolutionThe kinetic theory of gases states that the average squared velocity of molecules varies linearly with the mean molecular weight of the gas. If the root mean square (rms) velocity of oxygen molecules at a certain temperature is 0.5 km/sec. The rms velocity for hydrogen molecules at the same temperature will be :
View SolutionIf 2 mol of an ideal monatomic gas at temperature `T_(0)` are mixed with 4 mol of another ideal monatoic gas at temperature `2 T_(0)` then the temperature of the mixture is
View SolutionFrom the following statements concerning ideal gas at any given temperature T, select the correct one (s)
View SolutionFigure shows the pressure P versus volume V graphs for a certains mass of a gas at two constant temperature `T_(1) and T_(2)`. Which of the following interface is correct?
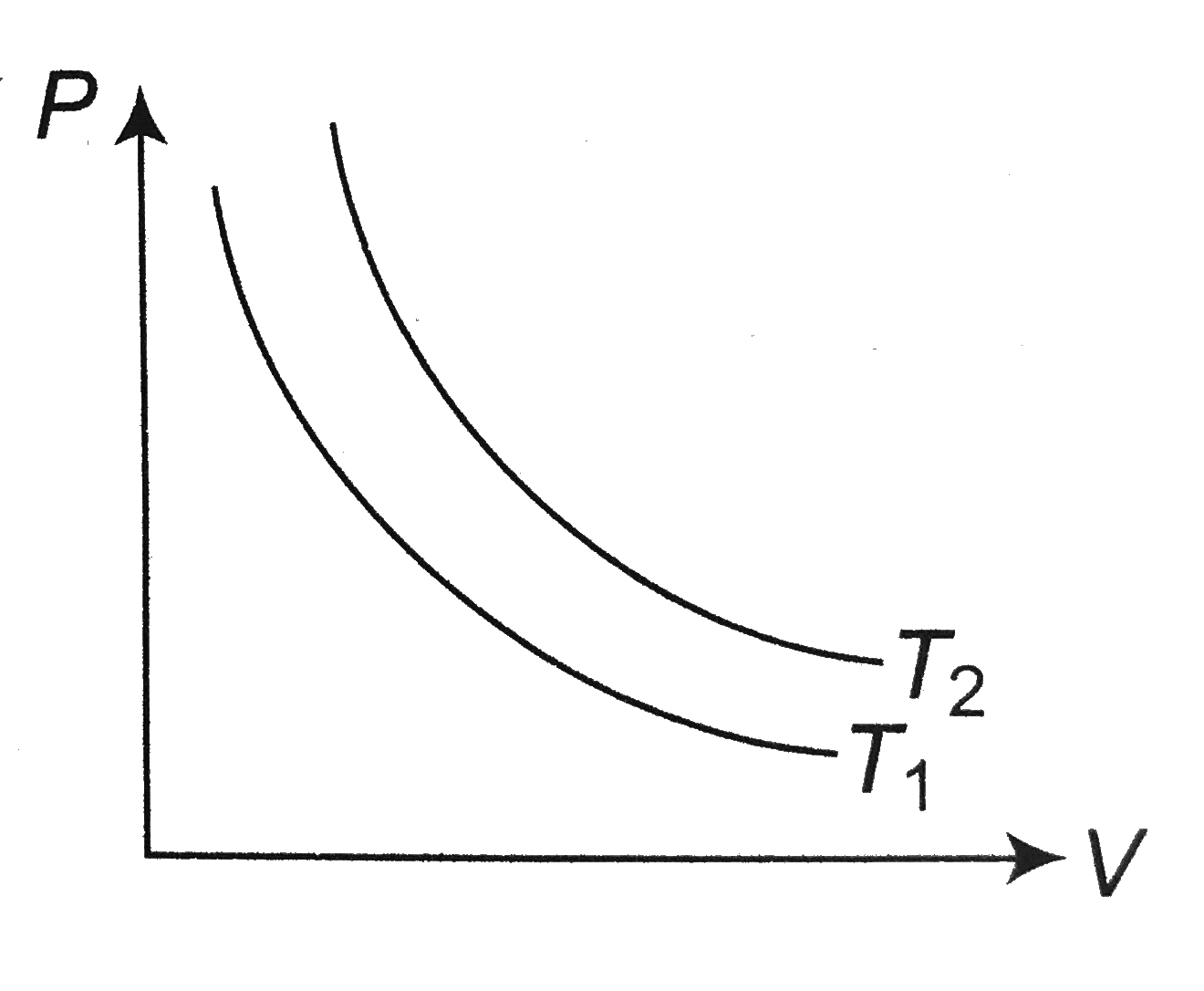
View SolutionThe molecules of a given mass of a gas have rms velocity of `200 m//s at 27^(@)C and 1.0 xx 10^(5) N//m_(2)` pressure. When the temperature and pressure of the gas are respectively `127^(@)C and 0.05 xx 10^(5) Nm^(-2)`, the rms velocity of its molecules in `ms^(-1)` is
View SolutionA graph is plotted with PV/T on y-axis and mass of the gas along x-axis for different gases. The graph is
View SolutionAt identical temperatures, the rms speed of hydrogen molecules is `4` times that for oxygen molecules. In a mixture of these in mass ratio `H_(2) : O_(2) = 1 : 8`, the rms speed of all molecules in n times the rms speed for `O_(2)` molecules, where n is
View SolutionFind the expression for the work done by a system undergoing isothermal compression (or expansion) form volume `V_(1)` to `V_(2)` at temperature `T_(0)` for a gas which obeys the van der waals equation of state. `(P +an^(2) //V^(2)) (V-bn) =nRT`?
View SolutionTwo vessel separately contains two ideal gases A and B at the same temperature, the pressure of A being twice that of B. under such conditions, the density of A is found to be 1.5 times the density of B. the ratio of molecular weight of A and B is
View SolutionThe temperature of the mixture of one mole of helium and one mole of hydrogen is increased from 0°C to 100°C at constant pressure. The amount of heat delivered will be
View SolutionIf the intermolecules forces vanish away, the volume occupied by the molecules contained in `4.5 kg` water at stantard temperature and pressure will be given by
View SolutionIf the intermolecules forces vanish away, the volume occupied by the molecules contained in `4.5 kg` water at stantard temperature and pressure will be given by
View SolutionA vessel has 6g of hydrogen at pressure P and temperature 500K. A small hole is made in it so that hydrogen leaks out. How much hydrogen leaks out if the final pressure is P/2 and temperature falls to 300 K ?
View SolutionFor a gas if ratio of specific heats at constant pressure and volume is g then value of degrees of freedom is
View SolutionThe given P-V curve is predicted by
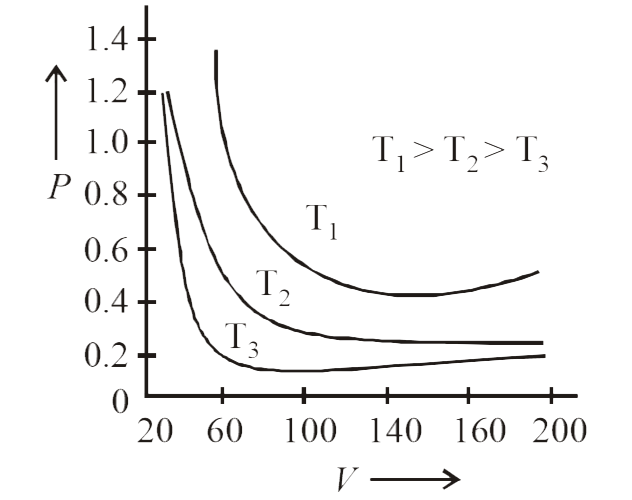
View SolutionThree perfect gases at absolute temperature `T_1,T_2, and T_3` are mixed. The masses of molecules are `n_1,n_2 and n_3` respectively. Assuming to loss of energy, the final temperature of the mixture is:
View SolutionA gas is enclosed in a cube of side l. What will be the change in momentum of the molecule, if it suffers an elastic collision with the plane wall parallel to yz-plane and rebounds with the same velocity ?
`[(V_(x), V_(y) & V_(z))` initial velocities of the gas molecules]
View SolutionWhat will be the ratio of number of molecules of a monoatomic and a diatomic gas in a vessel, if the ratio of their partial pressures is 5 : 3 ?
View SolutionThe average translational energy and the rms speed of molecules in a sample of oxygen gas at `300K` are `6.21xx10^(-21)J` and `484m//s`, respectively. The corresponding values at `600K` are nearly (assuming ideal gas behaviour)
View SolutionAt `10^(@)C`, the value of the density of a fixed mass of an ideal gas divided by its pressure is x. at `110^(@)C`, this ratio is
View SolutionIf the potential energy of a gas molecule is `U=(M)/(r^(6))-(N)/(r^(12)),M ` and `N` being positive constants, then the potential energy at equilibrium must be
View SolutionConsider a gas with density `'rho'` and `overlinec` as the root mean square velocity of its molecules contained in a volume. If the system moves as whole with velocity 'v' , then the pressure exerted by the gas is
View SolutionHow is the mean free path `(lambda)` in a gas related to the interatomic distance?
View SolutionFour molecules have speeds `2 km//s, 3 km//s, 4 km//s` and `5 km//s`. The `rms` speed of these molecules in `km//s` is
View SolutionIf `R = ` universal gas constant, the amount of heat needed to raise the temperature the temperature of `2 mol` of an ideal monatomic gas from `273 K` to `373 K` when no work is done is
View SolutionN molecules, each of mass m of gas `A and 2 N` molecules each of mass `2m` of gas `B` are containted in the same vessel which is maintained at temperature T. The mean square velocity of molecules of B type is denoted by `v^(2)` and the mean square velocity of A type is denoted by `(omega)^(2)`. the `omega^(2)//v^(2)` is:
View SolutionThe root mean square value of the speed of the molecules in a fixed mass of an ideal gas is increased by increasing
View SolutionP-V diagram of a diatomic gas is a straight line passing through origin. The molar heat capacity of the gas in the process will be
View SolutionFor a gas, difference between two specific heats is 5000 J/ mole°C. If the ratio of specific heats is 1.6, the two specific heats in J/mole-°C are
View Solution
PHYSICS questions and complete solutions for chapter KINETIC THEORY OF GASES of DISHA PHYSICS (HINGLISH) of Class 11