Complete Solutions to worked out Examples of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| HC VERMA | worked out Examples |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
A wheel rotates with a constant acceleration of `2.0(rad)/s^2`. If the wheel starts from rest, how many revolutions will it make in the first 10 seconds?
View SolutionThe wheel of a motor, accelerated uniformly from rest, rotates through 2.5 radian during the first second. Find the angle rotated during the next second.
View SolutionA wheel having moment of inertia 2 kg m^2 about its axis, rotates at 50 rpm about this axis. Find the torque that can stop the wheel in one minute.
View SolutionA string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m^2 and radius 20 cm. The wheel is free to rotate about it axis. Initially, the wheel is at rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
View SolutionA wheel of radius r and moment of inertia I about its axis is fixed at top of an inclined plane of inclination `theta` as shown in figure. A string is wrapped round the wheel and its free end supports a block of mass M which can slide on the plane. Initially, the wheel is rotating at a speed `omega` in direction such that the block slides up the plane. How far will the block move before stopping?

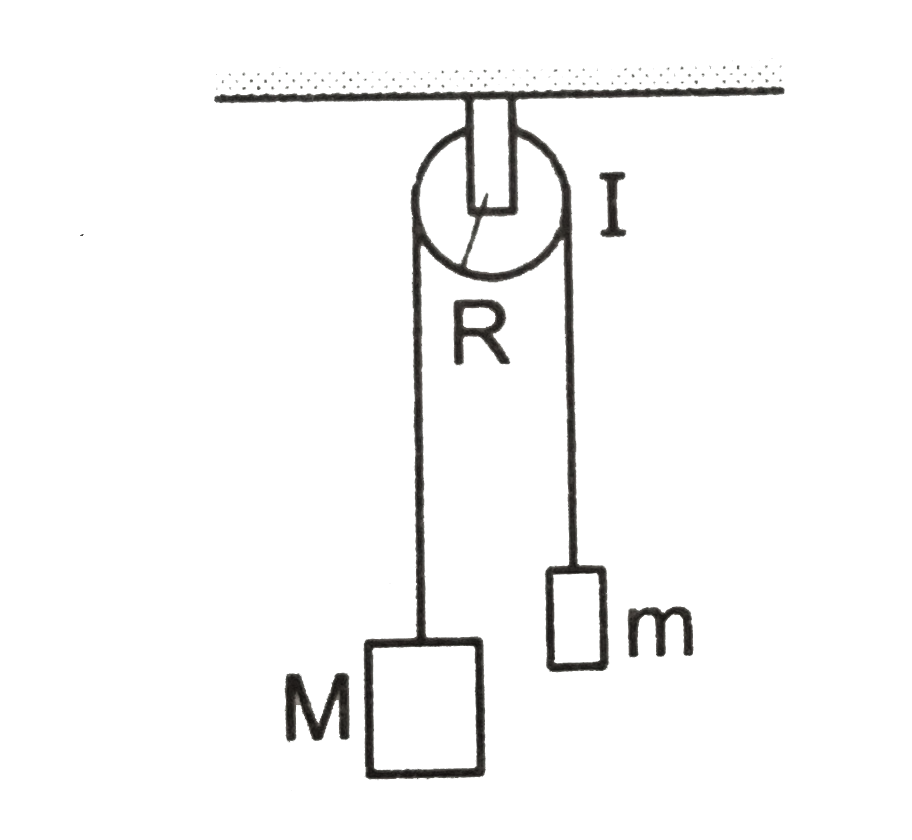
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
View SolutionTwo small kids weighing 10 kg and 15 kg respectively are trying to balance a seesaw of total length 5.0 with the fulcrum at the centre. If one of the kids is sitting at an end where should the other sit?
View SolutionA uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of `53^0` with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
View SolutionThe ladder shown in figure has negligible mass and rests on a frictionless floor. The crossbar connects the two legs of the ladder at the middle. The angle between the two legs is `60^0`. The fat person sitting on the ladder has a mas of 80 kg. Find the contact force exerted by the floor on each leg and the tension in the cross bar.
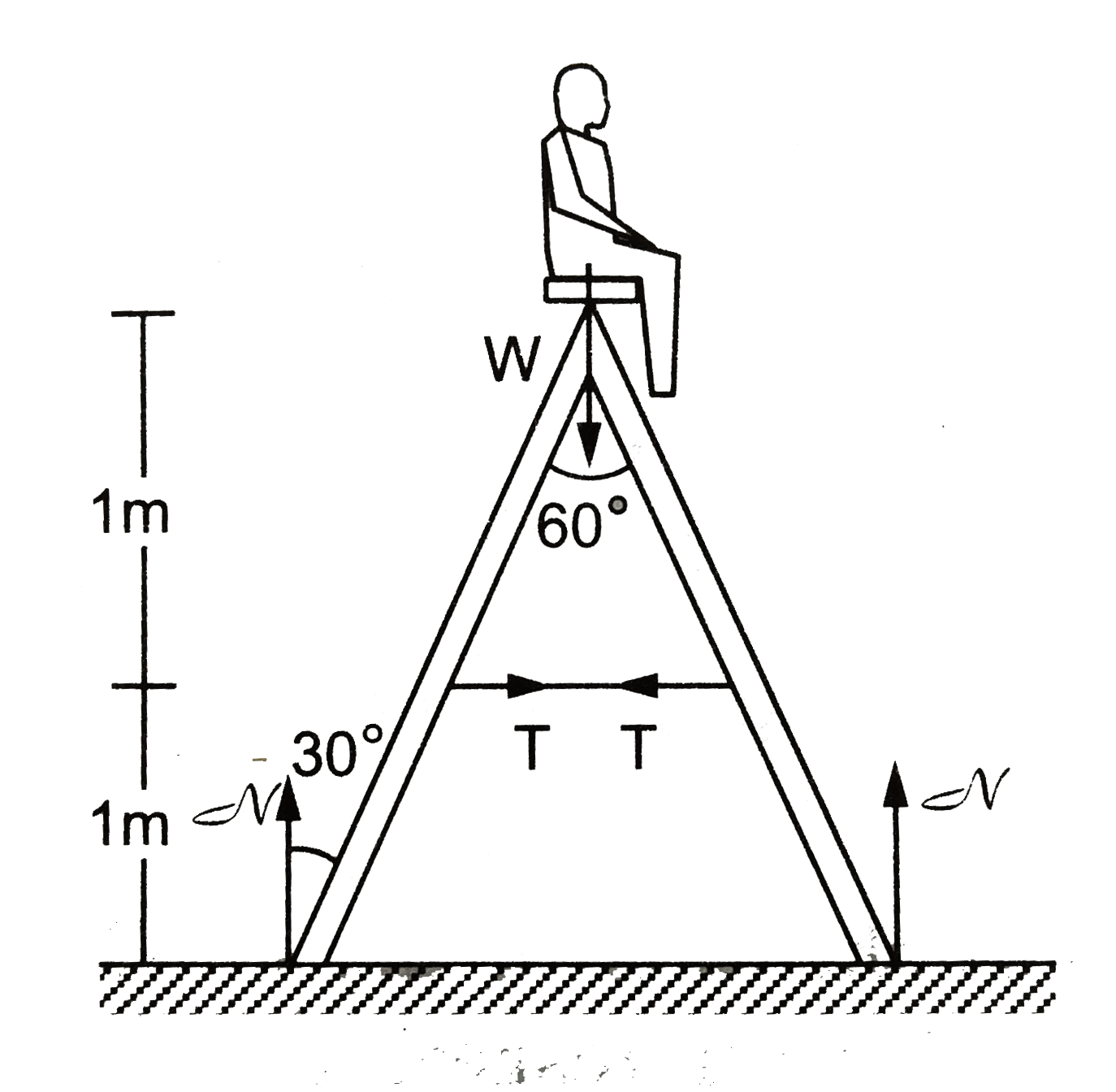
View SolutionTwo small balls A and B each of mass m, are attached tightly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed `omega`. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
View SolutionTwo particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end and is rotated in a plane at an angular speed `omega`. Calculate the angular momentum of the particle at the end with respect to the particle at the centre
View SolutionA particle is projected at time t=0 from a point P wilth a speed `v_0` at an angle of `45^@` to the horizontal. Find the magnitude and the direction of the angular momentum of the particle about the point P at time `t=v_0/g`
View SolutionA uniform circular disc of mass 200 g and radius 4.0 cm is rotated about one of its diameter at an angular speed of 10 rad/s. Find the kinetic energy of the disc and its angular momentum about the axis of rotation.
View SolutionA wheel rotating at an angular speed of 20 rad/s is brought to rest by a constant torque in 4.0 seconds. If the moment of inertia of the wheel about the axis of rotation is 0.20 `kg-m^2` find the work done by the torque in the first two seconds.
View SolutionTwo masses m and `M(m lt M)` are joined by a light string passing over a smooth and light pulley (as shown)

View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius `r_0` with a speed `v_0` and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View SolutionA uniform rod of mas m and length l is kept vertical with the lower end clamed. It is slightly pushed to let it fall down under gravity. Find its angular speed when the rod is passing through its lowest positon. Neglect any friction at the clamp. What will be the linear speed of the free end at this instant?
View SolutionFour particles each of mass 'm' are kept at the four corners of a square of edge 'a'. Find the moment of inertia of the system about a line perpendicular to the plane of the square and passing through the center of the square.
View SolutionTwo identical spheres each of mass 1.20 kg and radius 10.0 cm are fixed at the ends of a light rod so that the separation between the centers is 50.0 cm. Find the moment of inertia of the system about an axis perpendicular to the rod passing through its middle point.
View SolutionTwo uniform identicla rods each of mass M and length l are joined to form a cross as shown in figure. Find the momet of inertia of the cross about a bisector as shown doted in the figure

View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance `a/4` from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA wheel of perimeter 220 cm rolls on a level road at a speed of 9 km/h. How many revolutions does the wheel make per second?
View SolutionA cylinder is released from rest from the top of an incline of inclination `theta` and length 'L'. If the cylinder rolls without slipping. What will be its speed when it reaches the bottom?
View SolutionA sphere of mass m rolls without slipping on an inclined plane of inclination `theta`. Find the linear acceleration of the sphere and the force of friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?
View SolutionFigure shows two cylinders of radii `r_1 and r_2` having moments of inertia `I_1 and I_2` about their respective axes. Initially the cylinders rotate about their axes with angular speed `omega_1 and omega_2` as shown in the figure. The cylinders are moved closer to touch each other keeping the axes parallel. The cylinders first slip over each other at the contact but the slipping finally ceases due to the friction between them. Find the angular speeds of the cylinders after the slipping ceases.

View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.

View SolutionA force F acts tangentially at the highest point of a sphere of mass m kept on a rough horiozontal plane. If the sphere rolls withut slipping, find the accelerastioni of the centre of the sphere.
View SolutionA sphere of mass `M` and radius `r` shown in figure slips on a rough horizontal plane. At some instant it has translational velocity `V_(0)` and rotational velocity about the centre `(v_(0))/(2r)`. Find the translational velocity after the sphere starts pure rolling.
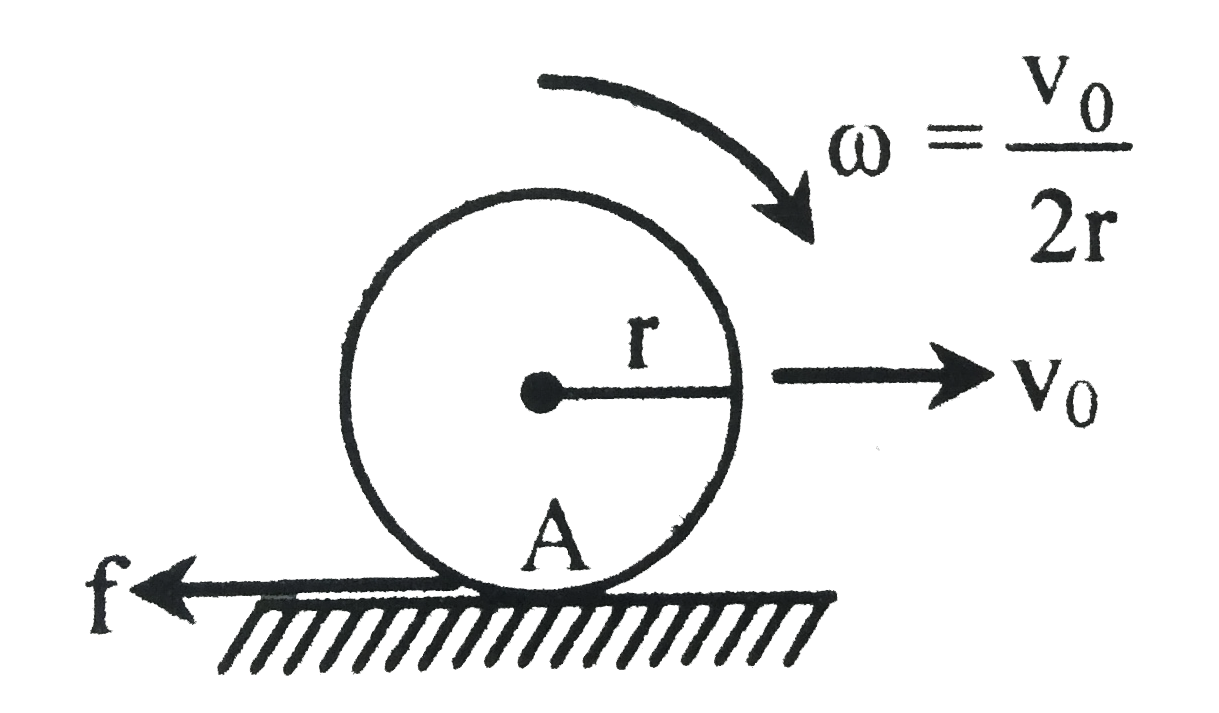 .
.
View SolutionThe sphere shown in figure lies on a rough plane when a particle of mass m travelling at a speed `v_0` collides and sticks with it. If the line of motion of the particle is at a distance h above the plane, find a. the linear speed o the combined system just after the collision b. the angular speed of the system about the centre of the sphere just the collision c. the value of h for which the sphere starts pure rolling on the plane Assume that the mass M of the sphere is large compared to the mass of the particle so that the centre of mass of the combined system is not appreciably shifted from the centre of the sphere.
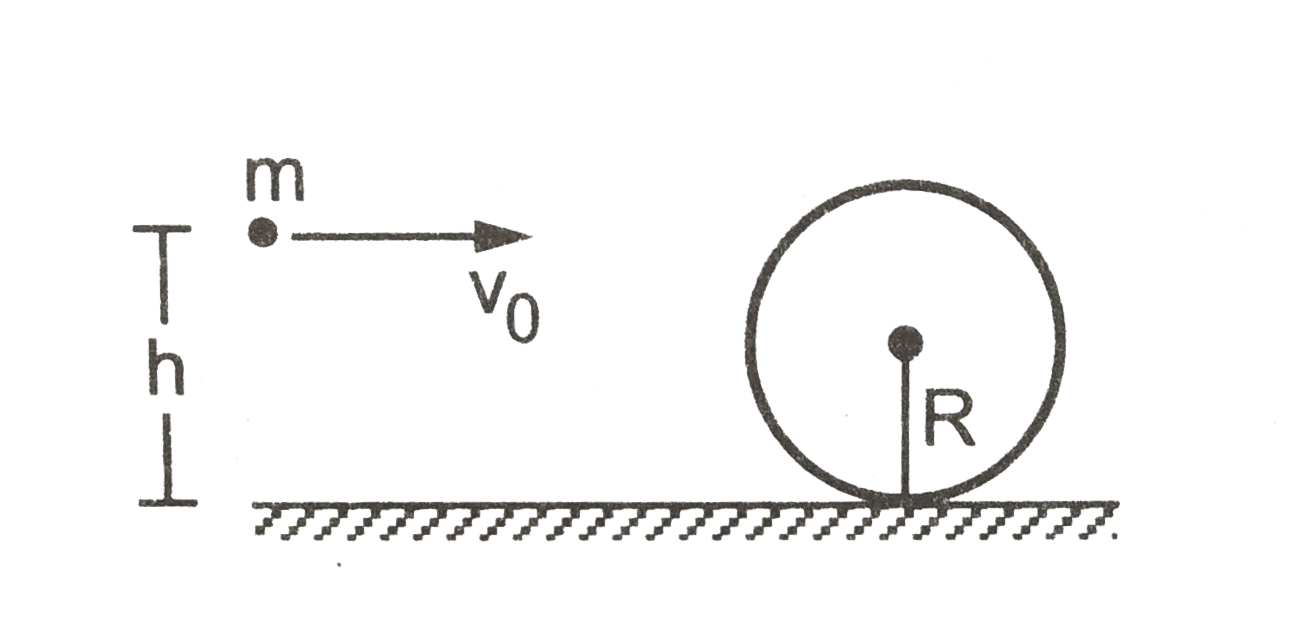
View Solution
worked out Examples questions and complete solutions for chapter ROTATIONAL MECHANICS of HC VERMA PHYSICS (ENGLISH) of Class 11