Complete Solutions to Exercises of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| HC VERMA | Exercises |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
A wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration. Find the angle rotated during these four seconds.
View SolutionA wheel rotating wilth unifrom angular acceleration covers 50 revolutions in the first five seconds after the start. Find the angular acceleration and the angular velocity at the end of five seconds.
View SolutionA wheel starting from rest is uniformly accelerate at 4 `rad /s^2` for 10 seconds. It is allowed to rotate uniformly for the next 10 seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.
View SolutionA body rotates about a fixed axis with an angular acceleration of one radian/second/second. Through what angle does it rotate during the time in which its angular velocity increases from 5 rad/s to 15 rad/s.
View SolutionFind the angular velocity of a body rotating with an acceleration of `2rev/s^2` as it completes the 5th revolution after the start
View SolutionA disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
a. a point on the rim,
b. the middle point of the radius.
View SolutionA disc rotates about its axis with a constant angular acceleration of `4rad/s^2`. Find the radial and tangential acceleration of a particle at a distance of 1 cm from the axis at the end of the first second after the disc starts rotating.
View SolutionA block hangs from a string wrapped on a disc of radius 20 cm free to rotate about its axis which is fixed in a horizontal position. If the angular speed of the disc is 10 rad/s at some instant, with what speed is the block going down at that instant?
View SolutionThree particles, each of mass 200 g are kept at the corners of an equilateral triangle of side 10 cm. Find the moment of inertia of the system about an axis
a. joining two of the particles
b. passing through one of the particle perpendicular to the plane of the particles.
View SolutionParticles of masses 1g, 2g, 3g ….100g are kept at the marks 1cm, 2cm, 3cm …., 100 cm respectively on a metre scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the metre scale.
View SolutionFind the moment of inertia of a pair of spheres, each having a mass m and radius r kept in contact about the tangent passing through the point of contact.
View SolutionThe moment of inertia of a uniform rod of mass 0.50 kg and length 1 m is 0.10 kg m^2 about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
View SolutionFind the radius of gyration of a circular ring of radius r about a line perpendicular to the plane of the ring and passing through one of this particles.
View SolutionThe radius of gyration of a uniform disc about a line perpendicular to the disc equals to its radius. Find the distance of the line from the centre.
View SolutionFind the moment of inertia of a uniform square plate of mass `M` and edge a about one of its diagonals.
View SolutionThe surface density (mass/area) of a circular disc of radius a depends on the distance from the centre as `rho(r)=A+Br.` Find its moment of inertia about the line perpendicular to the plane of the disc through its centre.
View SolutionA particle of mass m is projected with speed u at an angle `theta` with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA simple pendulum of length l is pulled aside to make an angle `theta` with the vertical. Find the magnitude of the torque of the weight w of the bob about the point of suspension. When is the torque zero?
View SolutionWhen a force of 6.0 N is exerted at `30^@` to a wrench at a distance of 8 cm from the nut, it is just able to losen the nut. What force F would be sufficient to loosen it if it acts perpendicularly to the wrench at 16 cm from the nut?

View SolutionFind the charge on the capacitor shown in figure
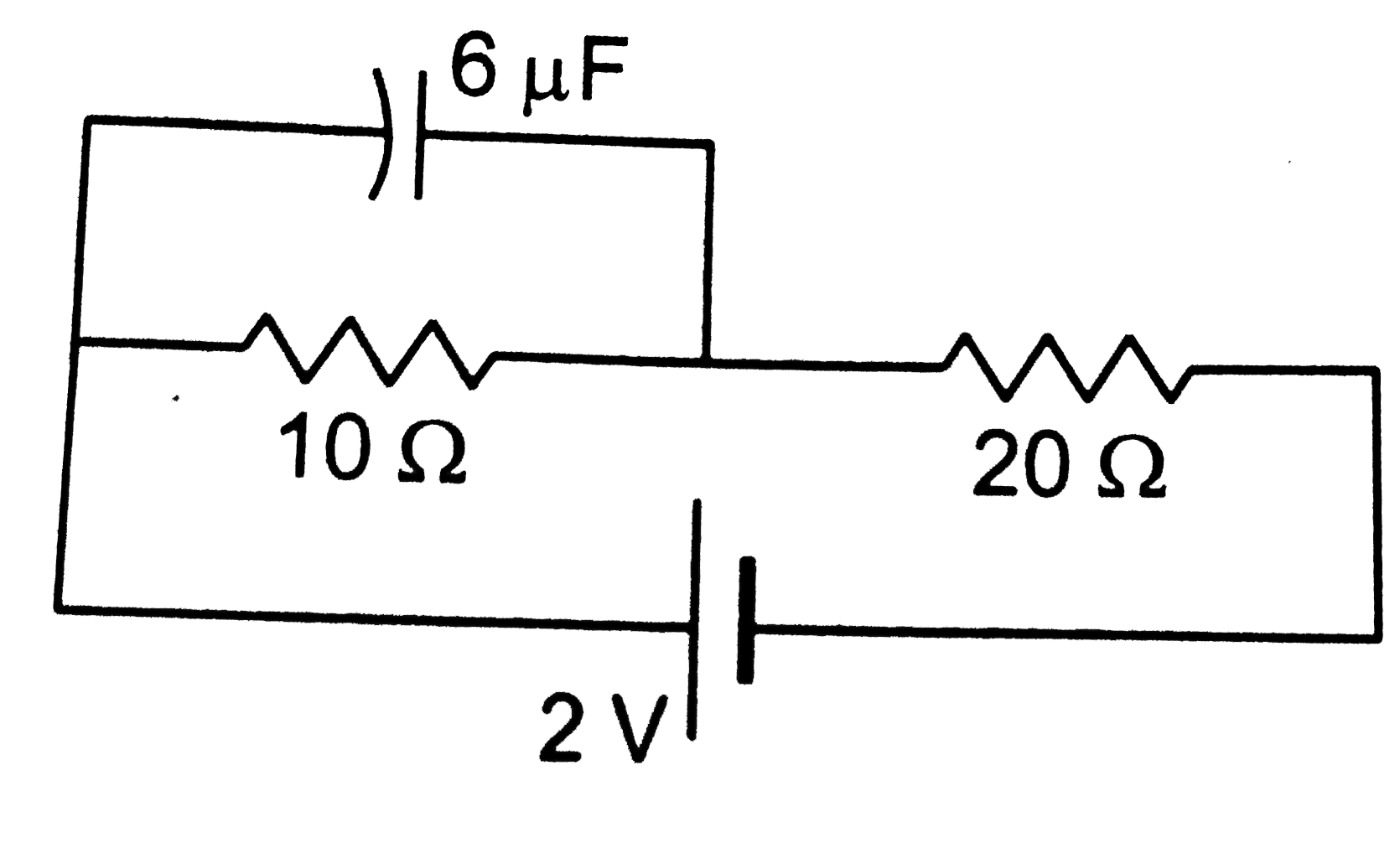
View SolutionA cubical block of mass M and edge a slides down a rougg inclined plane of inclination `theta` with a uniform velocity. The torque of the normal force on the block about its centre has magnitude.
View SolutionA rod of mass m and length L , lying horizontally is free to rotate about a vertical axis through its centre. A horizontal force of constant magnitude F acts on the rod at a distance of L/4 from the centre. The force is always perpendicular to the rod. Find the angle rotated by the rod during the time t after the motion starts.
View SolutionA square plate of mass 120g and edge 5.00 cm rotates about one of the edges. If it has a uniform angular acceleration of `0.2 rad/s^2`, what torque acts on the plate?
View SolutionCalculate the torque on the square plate of the previous problem if it rorates about a diagonal with the same angular acceleration.
View SolutionA flywheel of moment of inertia 5.0 kg m^2 is rotated at a speed of 60 rad/s. Because of the friction at the axle, it comes to rest in 5.0 minutes. Find a. The average torque of the friction. B. the total work done by the friction and c. the angular momentum of the wheel 1 minute before it stops rotating.
View SolutionBecause of the friction between the water in oceans with the earth's surface the rotational kinetic energy of the earth is continuously decreasing. If earth's angular speed decreases by 0.0016 rad/day in 100 years, find the average torque of the friction on the earth. Radius of the earth is 6400 km and its mass is `6.0xx10^24kg`.
View SolutionA flywheel rotating at a speed of `600` rpm about its axis is brought to rest by applying a constant torque for `10` seconds. Find the angular deceleration and angular velocity `5` second after the application of the torque.
View SolutionA wheel of mass 10 kg and radius 0.2 m is rotating at an angular speed of 100 rpm, when the motion is turned off. Neglecting the friction at the axis. Calculate the force that must be applied tangentially to the wheel to bring it to rest in 10 rev. Assumed wheel to be a disc.
View SolutionA cylinder rotating at an angular speed of 50 rev/s is brought in contact with an identical stationary cylinder. Because of the kinetic friction, torques act on the two cylinders, accelerating the stationary one and decelerating the moving one. If the common magnitude of the acceleration and deceleration be one revolution per second square, how long will it take before the two cylinders have equal angular speed?
View SolutionA body rotating at 20 rad/s is acted upon by a constant torque providing it a deceleration of `2(rad)/s^2`. At what time will the body have kinetic energy same as the initial value if the torque continues to act?
View SolutionA light rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in the figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.

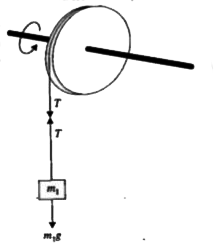
View SolutionA wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string.
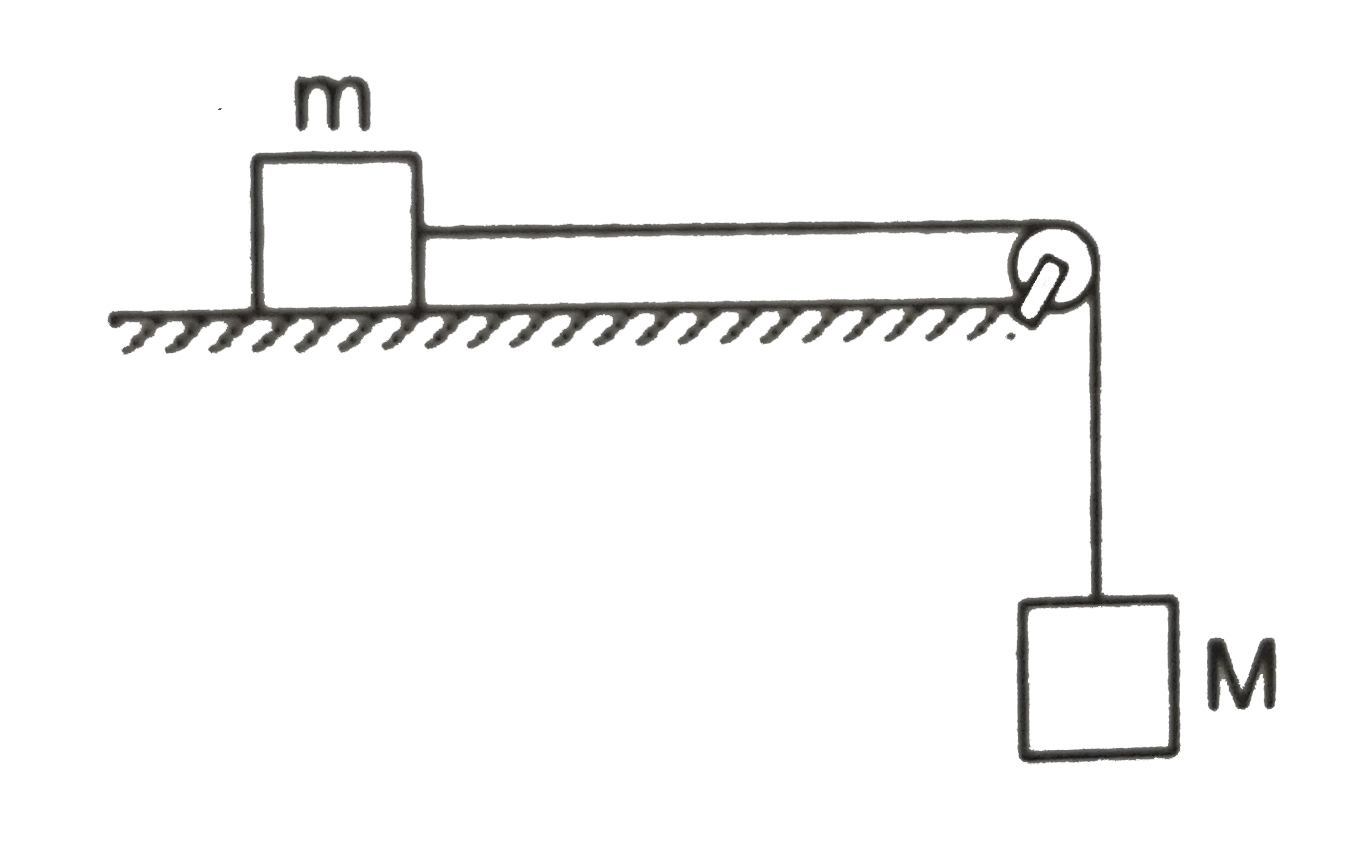
View SolutionFigure shows two blocks of masses m and M connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotate about this axis. Find the acceleration of the mass M assuming that the string does not slip on the pulley.
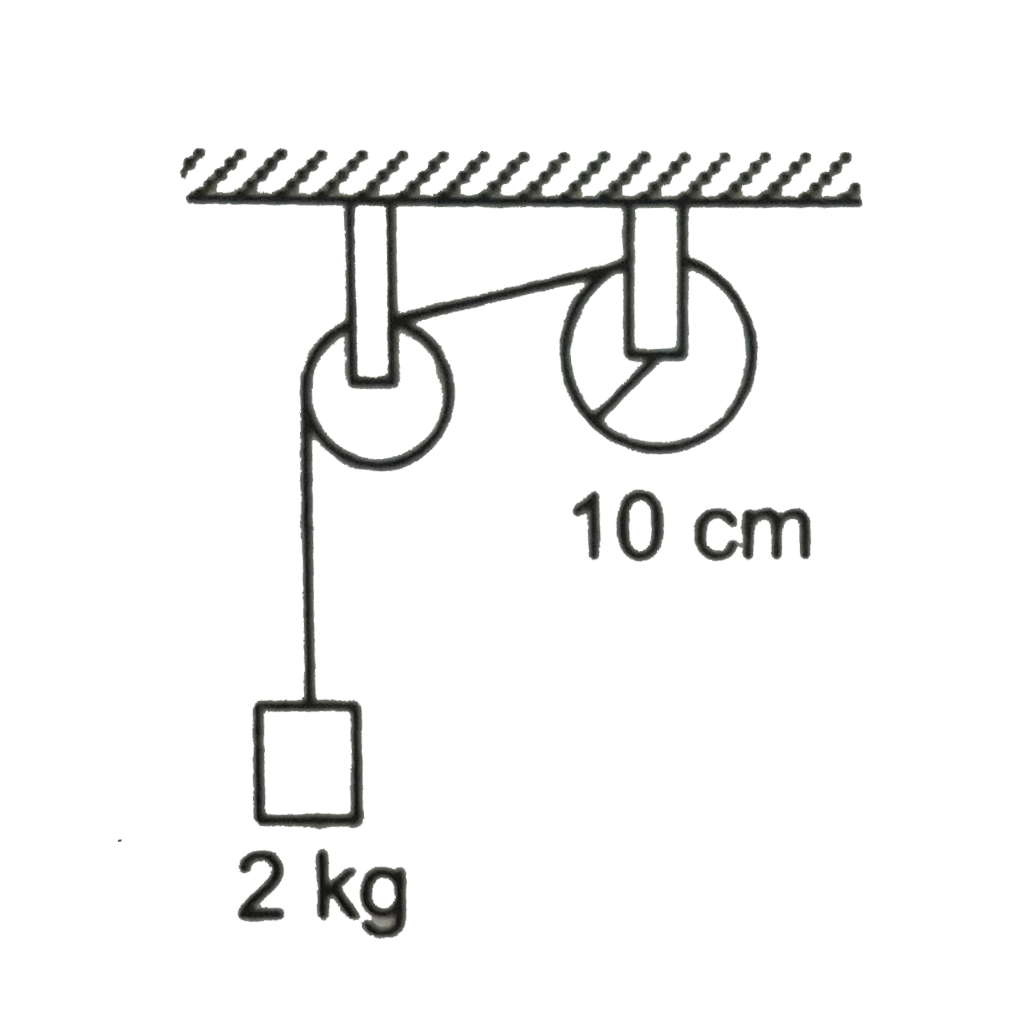
View SolutionA string is wrapped on a wheel of moment of inertia 0.20 kg-m^2 and radius 10 cm and goes through a light pulley to support a block of mass 2.0 kg as shown in figure. Find the acceleration of the block.
View SolutionSuppose the smaller pulley of the previous problem has its radius 5.0 cm and moment of inertia 0.10 kg-m^2. Find the tension in the part of the string joiningk the pulleys.
View SolutionThe pulleys in figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
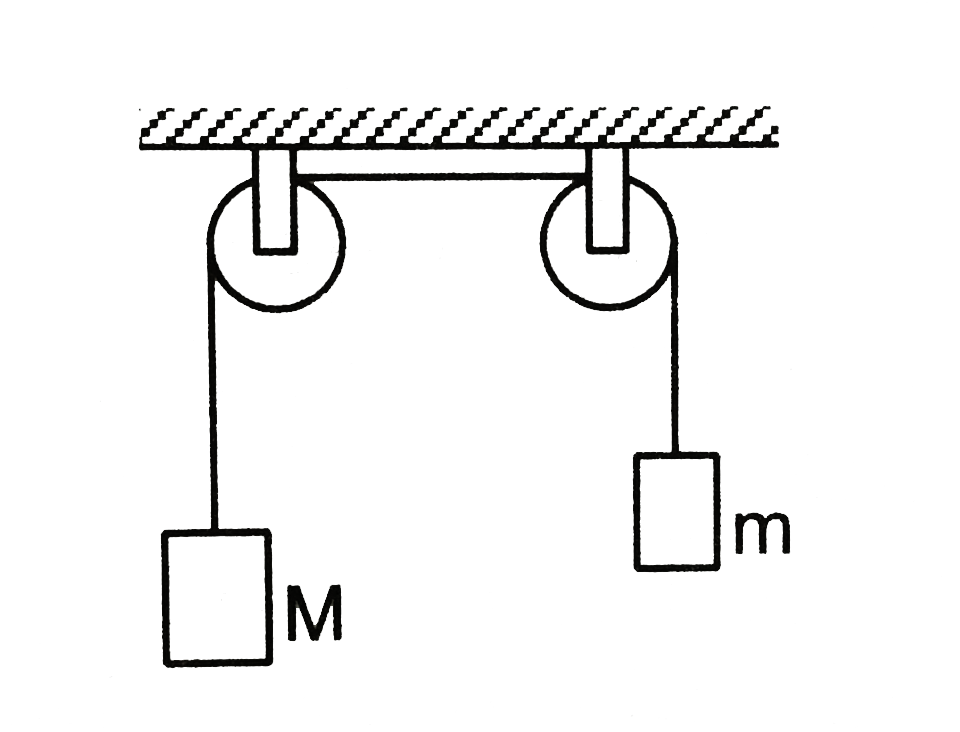
View SolutionThe pulleys in figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.

View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
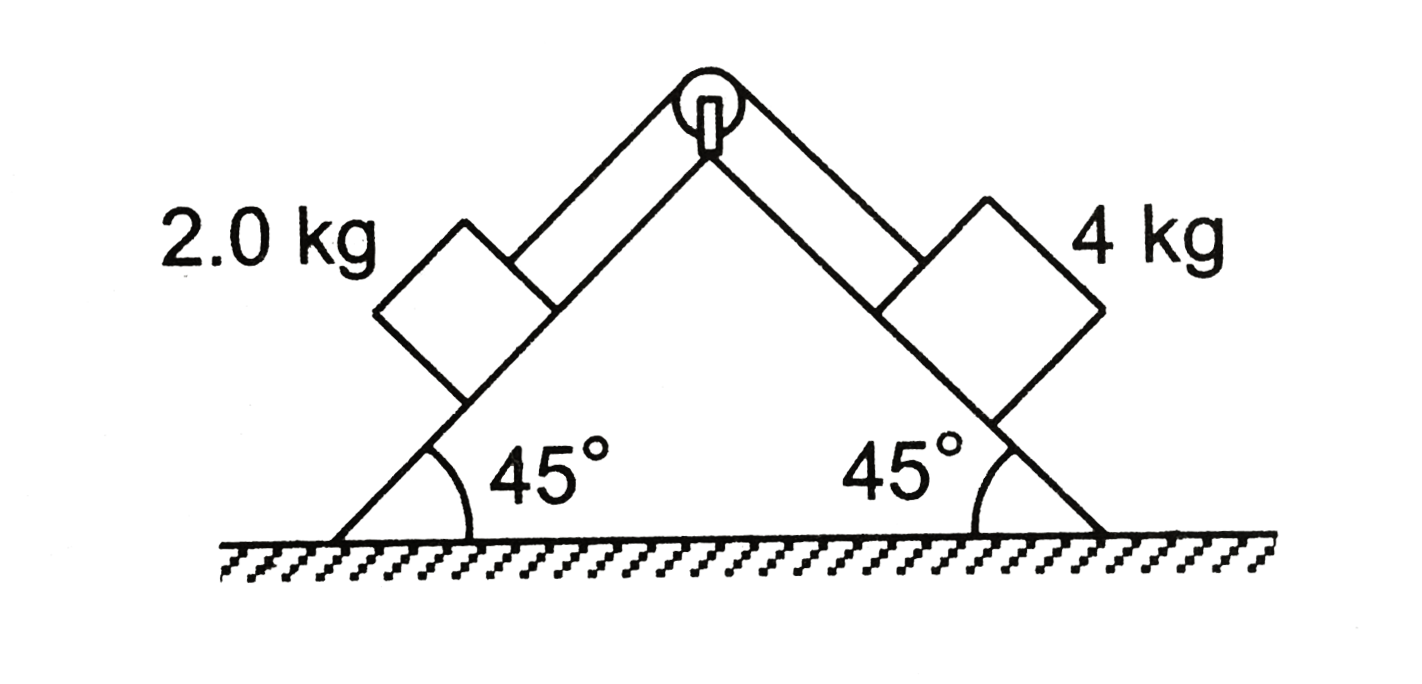
View SolutionSolve the previous problem if the firction coefficient between the 2.0 kg block and the plane below it is 0.5 and the plane below the 4.0 kg block is frictionless.
View SolutionA uniform metre stick of mass 200 g is suspended from the ceiling through two vertical strings of equal lengths fixed at the ends. A small object of mass 20 g is placed on the stick at a distance of 70 cm from the left end. Find the tensions in the two strings.
View SolutionA uniform ladder of length 10.0 m and mass 16.0 kg is resting against a vertical smooth wall making an angle of `37^@` with it. An electrian weighing 60.0 kg climbs up the ladder. If the stays on the ladder at a point 8.00 m from the lower end, what will be normal force and the force of friction on the ladder by the ground? What should be the minimum coefficient of friction for the electrician to work safely?
View SolutionSuppose the friction coefficient between the ground and the ladder of the previous problem is 0.540. Find the maximum weight of a mechanic who could go up and do the work from the same position of the ladder.
View SolutionA 6.5 m long ladder rests against as vertical wall reaching a height of 6.0 m. A 60 kg man stands hlf way up the ladder. A. Find the torque of the force exerted by the man on the ladder bout the upper end of the ladder. b.Assuming the weight of the ladder of be negligible as compared to the man and assuming the wall to be smooth find the force exerted by the ground on the ladder.
View Solutionthe door of an almirah is 6 ft high, 1.5 ft wide and weights 8 kg. The door is supported by two hinges situated at a distance of 1 ft from the ends. If the magnitude of the forces exerted by the hinges on the door are equal find this magnitude.
View SolutionA ladder of length `5 m` is placed against a smooth wall as shown in figure. The coefficient or friction is `mu` between ladder and ground. What is the minimum value of `mu` , If the ladder is not to slip?

View SolutionA uniform rod of mass 300 g and length 50 cm rotates at a uniform angular speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculate a. the angular momentum of the rod about the axis of rotation b. the speed of the centre of the rod and c. its kinetic energy.
View SolutionA uniform square plate of mass 2.0 kg and edge 10 cm rotates about one of its diagonals under the action of a constant torque of 0.10 Nm. Calculate the angular momentum and the kinetic energy of the plate at the end of the fifth second after the start.
View SolutionCalculate the ratio of the angular momentum of the earth about its axis due to its spinning motion to that about the sun due to its orbital motion. Radius of the earth =6400 km and radius of the orbit of the earth about the sun `=1.5xx10^8km.`
View SolutionTwo particles of masses `m_1 and m_2` are joined by a light rigid rod of length r. The system rotates at an angular speed `omega` about an axis through the centre of mass of the system and perpendicular to the rod. Show that the angular momentum of the system is `L=mur^2omega` where `mu` is the reduced mass of the system defined as `mu=(m_1m_2)/(m_1+m_2)`
View SolutionA dumb bell consists of two identicasl small balls offmss 1/2 kg each connected to the ends of a 50 cm long light rod. The dumb bell is rotating about a fixed axis through the centre of the rod and perpendicular to it t an angular speed of 10 rad/s. An impulsive force of average magnitude 5.0 N acts on one of the masses in the direction of its velocity for 0.10s. Find the new angular velocity of the system.
View SolutionA wheel of moment of inertia `0.500 kg-m^2` and radius 20.0 cm is rotating about its axis at an angular speed of 20.0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
View SolutionA diver having a moment of inertia of `6.0 kg-m^2` about an axis through its centre of mass rotates at an angular speed of 2 rad/s about this axis. If he folds his hands and feet to decrease the moment of inertia to 5.0 kg-m^2` what will be the new angular speed?
View SolutionA boy is seated in a revolving chair revolving at an angular speed of 120 revolutions per minute. Two heavy balls form part of the revolving system and the boy can pull the balls closer to himself or may push them apart. If by pulling the balls closer, the boy decreases the moment of inertia of the system from `6 kg-m^2 to 2 kg-m^2` what will be the new angular speed?
View SolutionA boy is sitting on a horizontal platform in the shape of a disc at a distance of 5m from its centre. The boy begins to slip when the speed of wheel exceeds 10 rpm. The coefficient of friction between the boy and platform is: `(g = 10 ms^(-2))`
View SolutionA wheel of moment of inertia `0.10 kg-m^2` is rotating about a shaft at an angular speed of `160 (rev)/(min)`. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with as common angular speed of 200 rev/minute. Find the moment of inertia of the second wheel.
View SolutionA kid of mass M stands at the edge of a platform of radius R which can be freely rotated about its axis. The moment of inertia of the platform is I . The system is at rest when a friend throws as ball of mass m and the kid catches it. If the velocity of the ball is v horizontally along the tangent to the edge of the platform when it was caught by the kid find the angular speed of the platform after the event.
View SolutionSuppose the platform of the previous problem is brought to rest with the ball in tehhad of the kid standin on the rim. The kid throuws the ball horizontaly to his friend in a direction tangentiasl to the rim with a speed v as seen by his friend. Find the angular velocity wilth which the platform will start rotating.
View SolutionSuppose the platform with the kid in the previous problemis rotting in anticlockwise directioin at an angular speed `omega`. The kid starts walking along the rim with a speed v relative to the platform also in the anticlockwise direction. Find the new angular speed of the platform.
View SolutionA uniform rod of mass m and length l is struck at an end by a force F perpendicular to the rod for a short time interval t. Calculate
a. the speed of the centre of mass ,b. the angular speed of the rod about centre of mass, c. the kinetic energy of the rod and d. the angular moment of the rod about the centre of mass after the force has stopped to act. Assume that t is so small that the rod does not apreciably change its direction while the force acts.
View SolutionA uniform rod of length L lies on a smooth horizontal table. A particle moving on the table strikes the rod perpendicularly at an end and stops. Find the distance travelled by the centre of the rod by the time it turns through a right angle. Show that if the mass of the rod is four times that of the particle, the collision is elastic
View SolutionSuppose the particle of the previous problem has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M. a. Find the velocity of the particle with respect to C of the system consituting the rod plus the particle. b. Find the velociyt of the particle with respect to C before the collision. c. Find the velocity of the rod with respect to C before the colision. e. find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. f. Find the velociyt of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View SolutionTwo small bals A and B, each of mass m, are joined rigidlyl by a light horizontal rol of lengh L. The rod is clasmped at the centre in such a way that it c an rotate freely about a verticl axis through its centre. The systemis rotated with an angualr speed `omega` about the axis. A particle P of masss m kept at rest sticks to the ball A as the ball collides with it. Find the new angular speed of the rod.
View SolutionTwo small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity `v_0` in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.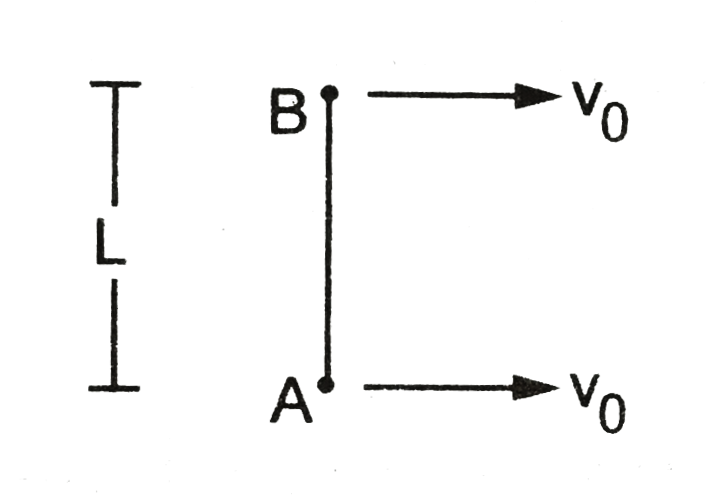
View SolutionSuppose the rod with the balls A and B of theprevious problem is clamped at the centre in such a way that it ca rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a heigh h hon the ball B. The particle collides with B and sticks to it. a. Find the angular momentum and the angular speed of the system just after the collision. b. What should be the minimum value of h so that the system makes a full rotation after the collision.
View SolutionTwo masses M and m are connect by a light string gong over a pulley of radis r. The pulley is free to rotate about its axis which is kept horizontal. The moment of inertia of the pulley about the axis is I. The system is releaed from rest. Find the angular momentum fo teh system when teh mass Mhas descended through a height h. The string does not slip over the pulley.
View SolutionThe pulley shown in figure has a radius of 20 cm and moment of inertial 0.2 kg-m^2. The string going over it is attached at one end to a vertical sprign of spring constant 50 N/m fixed from below and supports a 1 kg mas at other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has desceds through 10 cm. Take `g=10 m/s^2`.
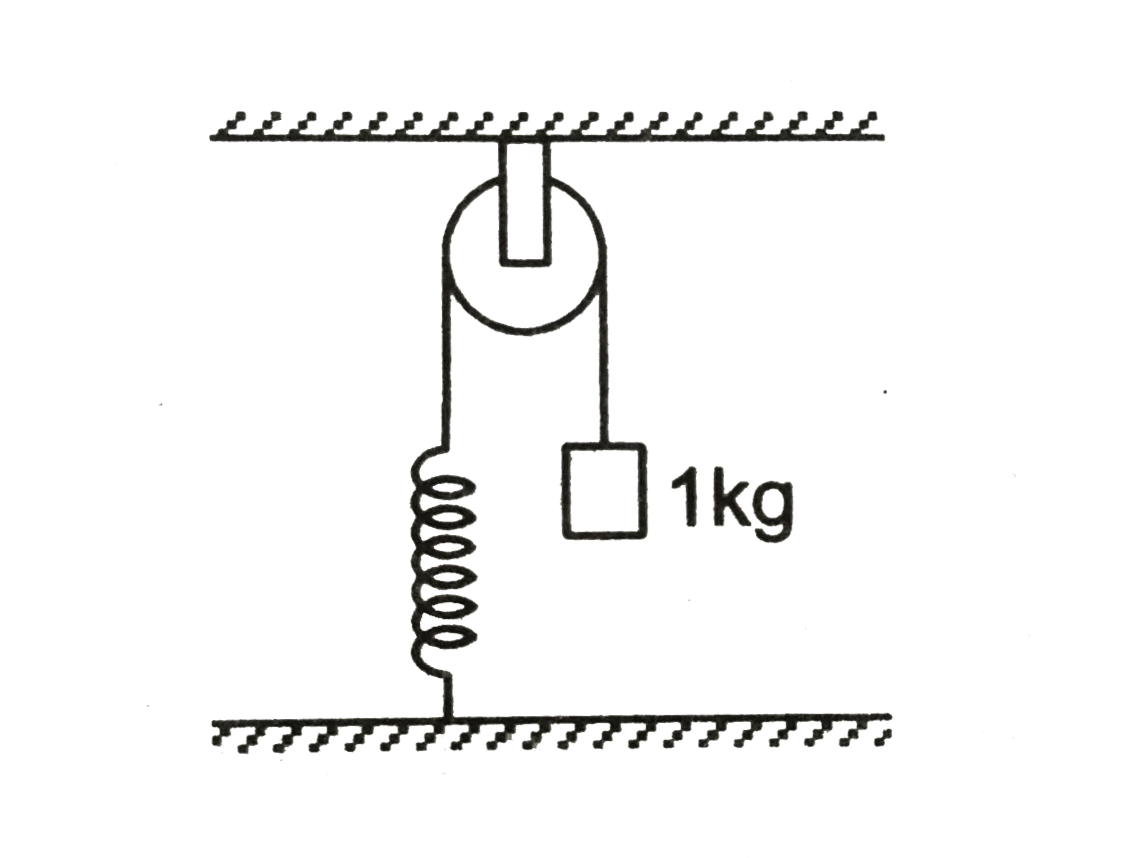
View SolutionA metre stick is is held verticaly with one end on a rough horizontal floor. It is gently alowed to fal on the floor. Assuming that the end ast the floor does not slip find the angular speed of the rod when it hits the floor.
View SolutionA metre stick weighing 240 g is pivoted at its upper end in such a way that it can freely rotate in a vertical plane through this end figure. A particle of mass 100 g is attached to the upper end of the stick through a light sting of length 1 m. Initially the rod is kept veritcal and the string horizontal when the system is released from rest. The particle colides with the lower end of the stick and sticks there. Find the maximum angle through which the stick will rise.

View SolutionA uniform rod is placed vertically on a smooth surface and then released . Then,
View SolutionA cylinder rolls on a horizontal plane surface. If the speed of the centre is 25 m/s, what is the speed of the highest point?
View SolutionA sphere of mass m rolls on a plane surface. Find its kinetic energy at an instant when its centre moves with speed v.
View SolutionA string is wrapped over the edge a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
View SolutionA small spherical ball is released from a point at a height h on a rough track shown in figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.

View SolutionA small disc is set rolign wioth a speed v on the horizontal part of the track of the previous problem from right to left. To what height will it climb up the curved part?
View SolutionA sphere starts rolling down can incline of inclination theta. Find the speed of its centre when it has covered a distance l.
View SolutionA hollow sphere is released from the top of an inlcined plane of inclination `theta`. A. What should be the minimum coefficientof friction between the shphere and the plane to prevent sliding? B. Find the kinetic energy of the ball as it moves down a length l on the incline if the friction coefficient is half the value calculated in part a.
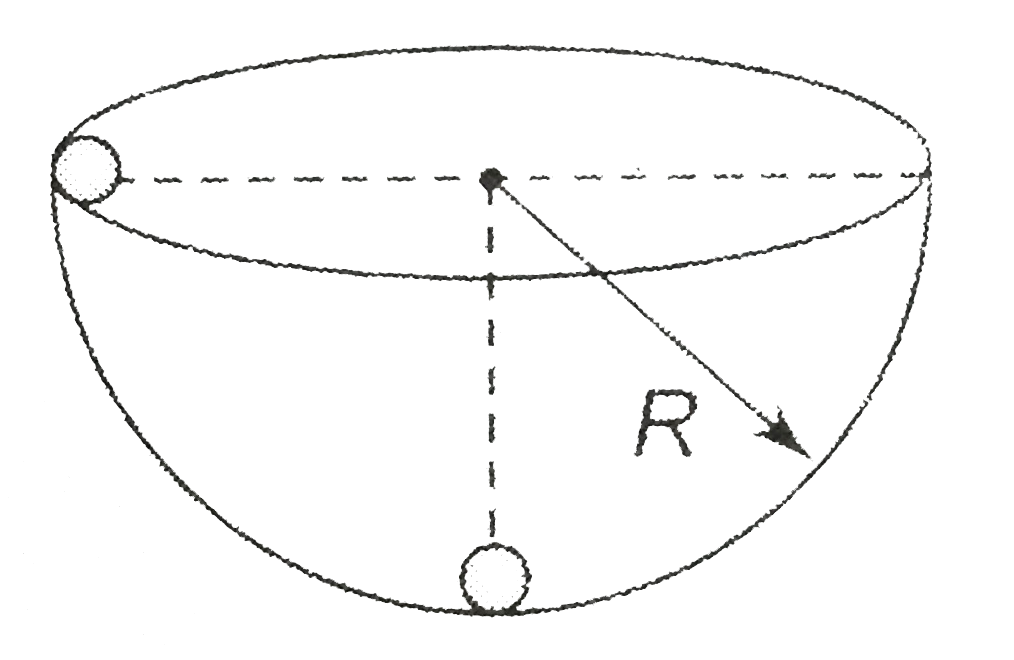
View SolutionConsider the situation as shown in the figure. A solid sphere of mass `m` is released from rest from the rim of a hemispherical cup so that it rolls along the surface. Find the normal contact force between the solid sphere and the cup at the bottom most point.
View SolutionFigure shows a rough track a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should as sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.

View SolutionFigure shows a smasll sphereical bal of mass m rolling down the loop track. Thebasll is released on the linear portion at a verticla height H from the lowest point. The circular part show has a radius R.
a. find the kinetic energy of the ball when it is at a point where the radius makes an angle `theta` with the horizontal.
Find the radial and the tangential accelerations of the cente when the ball is at A. c. find the bnormal force and the frictionasl force acting on the ball if H=60 cm, R=10cm `theta=0` and m=70 fg.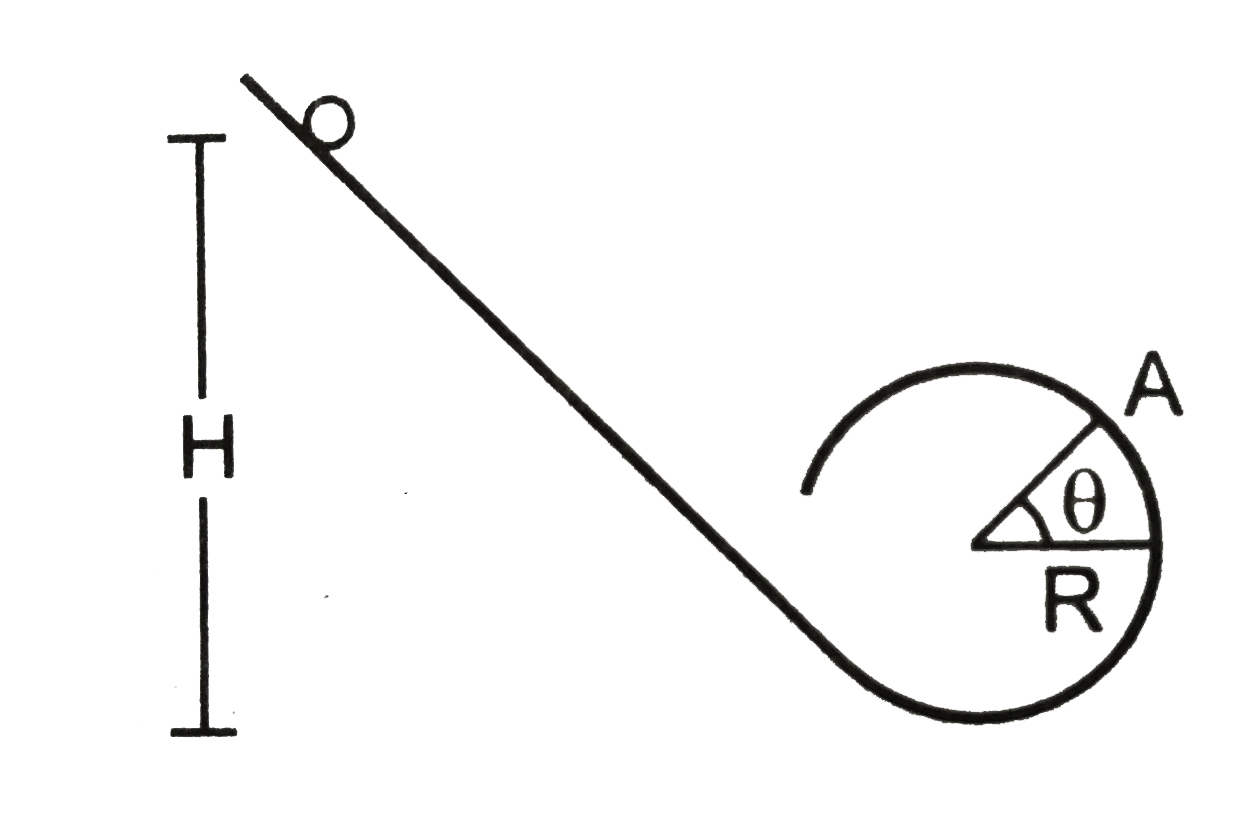
View SolutionA thin spherical shell of radius `R` lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity `v_(0)` and an angular velocity `omega _(0)` as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View SolutionA uniform wheel of radius R is set lying on a rough horizontal surface is hit by as cue is such a way that the line of action passes thruogh the centre of the shell. As a result the shelll starts movign with a linear speed v without any initial angular velocity. Find the linear speed of the shell after it starts pure rolling on the surface.
View SolutionA holow sphere of radius R lies on a smoth horizontal surface. It is pulle dby a horizontl force acting tasngentially from the highest point. Find the distance travelled by the sphere durint eh time it makes oen full rotation.
View SolutionA solid sphere of mass 0.50 kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
View SolutionA solid sphere is set into motion on a rough horizontal surfce with a linar speed v in the forward direction and an angular speed v/R in the anticlockwise direction as shown infigure . Find the linear speed of the sphere a. where it stops rotating and b. when slipping finally ceases sand pure rolling starts.

View SolutionA solid sphere rolling on a rough horizontl surface with a lilner speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View Solution
Exercises questions and complete solutions for chapter ROTATIONAL MECHANICS of HC VERMA PHYSICS (ENGLISH) of Class 11