Complete Solutions to SECTION-B of chapter MOTION IN A STRAIGHT LINE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A STRAIGHT LINE |
| KUMAR PRAKASHAN | SECTION-B |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
A car is moving along a straight line, say OP in It move from O to P in 18 s and returns from P to Q in ` 6 s`, where OP=360 m and OQ=240 m. What are the average velocity and average speed of the car in going (a) from O to P ? And (b) from O to P and back to Q ?
View SolutionA car moving in a straight line at a speed of 120 km covers in 2 hours. There after from that left side it covers 50 km in 1 hours. At that moment its average speed and aveerage velocity will ……. And ……
View SolutionThe position of an object moving along x-axis is given by `x =a + bt ^(2)` where `a 8.5 m, b =2.5 ms ^(-2)` and t is and `t = 2.0 s.` What is the average velocity between `t = 2.0 s and t = 4.0s ` ?
View SolutionThe positon of an object moving along x-axis is given by `x(t) = (4.2 t ^(2) + 2.6) m,` then find the velocity of particle at `t =0s and t =3s,` then find the average velocity of particle at t =0 s ` to `t =3s.
View SolutionObtain equations of motion for constant acceleration using method of calculus.
View SolutionA ball is thrown vertically upwards with a velocity of `20 ms^(-1)` from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take `g = 10 ms^(-2)`.
View SolutionDiscuss the motion of an object under free fall. Neglect air resistance.
View SolutionThe distance traversed, during equal intervals of time, of a body falling from rest, stand to one another in the same ratio as the odd numbers beginning with unity[ namely,` 1:3:5:7….].`Prove it.
View SolutionStopping distance of vehicles : When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity `(upsilon_(0))` and the braking capacity, or deceleration, `-a` that is caused by the braking. Derive an expression for stopping distance of a vehicle in terms of `upsilon_(0)` and a.
View SolutionWhat will be distance covered byu vehicle after applying breakes with retardation `8 m//s ^(2) ` if its velocity is 72 km/h ?
View SolutionWhat will be distance covered by vehicle after applying brakes with retardation `2m //s^(2) ` if its velocity is `1.8 km//h` ?
View SolutionWhen a situation demands our immediate action, it takes some time before we really respond. Reaction time is the time a person takes to observe, think and act. For example, if a person is driving and suddenly a boy appears on the road, then the time elapsed before he slams the brakes of the car is the reaction time. Reaction time depends on complexity of the situation and on an individual. You can measure your reaction time by a simple experiment. Take a ruler and ask your friend to drop it vertically through the gap between your thumb and forefinger . After you catch it, find the distance d travelled by the ruler. In a particular case, d was found to be 21.0 cm. Estimate reaction time.
View SolutionWhen a situation demands our immediate action, it takes some time before we really respond. Reaction time is the time a person takes to observe, think and act. For example, if a person is driving and suddenly a boy appears on the road, then the time elapsed before he slams the brakes of the car is the reaction time. Reaction time depends on complexity of the situation and on an individual. You can measure your reaction time by a simple experiment. Take a ruler and ask your friend to drop it vertically through the gap between your thumb and forefinger as shown in figure. After you catch it, find the distance d travelled by the ruler. In a particular case, d was found to be 21.0 cm. Estimate reaction time.

View SolutionTwo parallel rail tracks run north-south. Train A moves north with a speed of `54 km h^(-1)`, and train B moves south with a speed of `90 km h^(-1)`. What is the
(a) velocity of B with respect to A ?,
(b) velocity of ground with respect to B ?, and
(c) velocity of a monkey running on the roof of the train A against its motion (with a velocity of `18 km h^(-1)` with respect to the train A) as observed by a man standing on the ground ?
View SolutionTwo parallel rail tracks are in north-south direction. Train A moves towards north with a speed of 72 `kmh^(-1)` and train B moves towards south with a speed of 108 `kmh^(-1)` What is the (a) velocity of B with respect to A ?, (b) velocity of ground with respect to B ? and (c) velocity of a monkey running on the roof of the train A against its motion (with a velocity of 27 `kmh^(-1)` with respect to the train A) as observed by a man standing on the ground?
View SolutionIn which of the following examples of motion, can the body be considered approximately a point object :
(a) a railway carriage moving without jerks between two stations.
(b) a monkey sitting on top of a man cycling smoothly on a circular track.
(c) a spinning cricket ball that turns sharply on hitting the ground.
(d) a tumbling beaker that has slipped off the edge of a table.
View SolutionThe position-time (x-t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown in figure. Choose the correct entries in the brackets below,
(a) (A/B) lives closer to the school than (B/A)
(b) (A/B) starts from the school earlier than (B/A)
(c) (A/B) walks faster than (B/A)
(d) A and B reach home at the same! different) time

View SolutionA woman starts from her home at 9.00 am, walks with a speed of `5 km h ^(-1)` on a straight road up to her office 2.5 km away, stays at the office up to 5.00 pm, and returns home by an auto with a speed of `25 kmh^(-1).` Choose suitable scales and plot the x-t graph of her motion.

View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x-t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
View SolutionA vehicle covers certain distance at constant speed of `20 km h^(-1)` in time interval 't' on linear path. Then it covers certain distance at constant speed of `30 km h^(-1)` in the same time interval. What is the average speed of the vehicle ?
View SolutionA car moving along a straight highway with speed of `126 km h^(-1)` is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop ?
View SolutionTwo trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of `72 km h^(-1)` in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by `1 m s^(-2)`. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them ?
View SolutionOn a two-ane road, car A is travelling with a speed of `36 km h ^(-1).` Two cars B and C approach car A in opposite directions with a speed of `54 km h ^(-1)` each. At a certain instant, when the distance AB is equal to AC, both being 1 km, B decides to overtake A before C does. What minmum acceleration of car B is required to avoid an accident ?

View SolutionTwo towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 km` h^(-1)` in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road ?
View SolutionA player throws a ball upwards with an initial speed of 29.4 `ms^(-1)`
(a) What is the direction of acceleration during the upward motion of the ball ?
(b) What are the velocity and acceleration of the ball at the highest point of its motion ?
(c) Choose the x = 0 m and t=0 s to be the location and time of the ball at its highest point vertically downward direction to be the positive direction of x-axis and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
(d) To what height does the ball rise and after how long does the ball return to the player's hands ? (Take g = 9.8 `ms^(-2)` and neglect air resistance).
View SolutionRead each statement below carefully and state with reasons and examples, if it is true or false, A particle in one-dimensional motion
(a) with zero speed at an instant may have non-zero acceleration at that instant
(b) with zero speed may have non-zero velocity
(c) with constant speed must have zero acceleration,
(d) with positive value of acceleration must be speeding up.
View SolutionA ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between `t =0` to 12 s.
View SolutionExplain clearly, with examples, the distinction between : (a) magnitude of displacement (sometimes called distance) over an interval of time, and the total length of path covered by a particle over the same interval,
(b) magnitude of average velocity over an interval of time, and the average speed over the same interval. (Average speed of a particle over an interval of time is defined as the total path length divided by the time interval]. Show in both (a) and (b) that the second quantity is either greater than or equal to the first. When is the equality sign true ? (For simplicity, consider onedimensional motion only).
View SolutionA man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km`h^(-1).` Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km `h^(-1).` What is the (a) magnitude of average velocity, and (b) average speed of the man over the interval of time (i) 0 to 30 min, (ii) 0 to 50 min, (iii) 0 to 40 min ? [Note: You will appreciate from this exercise why it is better to define average speed as total path length divided by time, and not as magnitude of average velocity. You would not like to tell the tired man on his return home that his average speed was zero !]
View SolutionIn Exercises 3.13 and 3.14, we have carefully distinguished between average speed and magnitude of average velocity. No such distinction is necessary when we consider instantaneous speed and magnitude of velocity. The instantaneous speed is always equal to the magnitude of instantaneous velocity. Why?
View SolutionLook at the graphs (a) to (d) (Fig. 3.20) carefully and state, with reasons, which of these cannot possibly represent onedimensional motion of a particle.
View SolutionFigure shows the x-t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for `l lat 0` and on a parabolic path for `t gt 0` ? If not, suggest a suitable physical context for this graph.
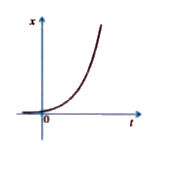
View SolutionA police van moving on a highway with a speed of `30 kmh^(-1)` fires a bullet at a thief's car speeding away in the same direction with a speed of `192 kmh^(-1).` If the muzzle speed of the bullet is `150 ms^(-1)` with what speed does the bullet hit the thief's car ? (Note: Obtain that speed which is relevant for damaging the thief's car).
View SolutionThe idea of secondary wavelets for the. propagation of a wave was first given by
View SolutionFigure gives the `x to t` plot of a particle executing one-dimensional simple harmonic motion. (you will learn about this motion inmore detail in Chapter 14). Give the signs of position, velocity and acceleration variables of the particle at `t =0.3s, 1.2 s, -1.2s.`

View SolutionFigure gives the x-t plot of a particle in one dimensional motion. Three different equal intervals of time are shown. In which interval is the average speed greatest and in which is it the least ? Give the sign of average velocity for each interval.

View SolutionFigure gives a speed - time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude ? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion give the signs of vand a in the three intervals. What are the acclerations at the points A, B, C and D?

View SolutionA three wheeler starts from rest, accelerates uniformly with 1 ms-2 on a straight road for 10 s and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1, 2, 3, ...) versus n. What do you expect this plot to be during accelerated motion : a straight line or a parabola ?
View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can equal to 49 ms-1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5 `ms^(-1)` and the boy again throws the ball up with the maximum speed he can, how long goes the ball take to return to his hands ?
View SolutionOn a long horizontally moving belt (From figure) a child runs to and fro with a speed 9 `kmh^(-1)` (with respect to the belt) between his father and mother located 50 m apart on the moving belt. The belt moves with a speed of 4 kmh-l. For an observer on a stationary platform outside, what is the
(a) Speed of the child running in the direction of motion of the belt ?
(b) Speed of the child running opposite to the direction of motion of the belt ?
(c) Time taken by the child in (a) and (b) ? Which of the answers alter if motion is viewed by one of the parents ?
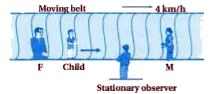
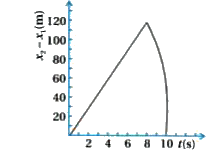
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 `ms^(- )`and 30 `ms^(-1).` Verify that the graph shown in figure. Correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 `ms^(-2).` Give the equations for the linear and curved parts of the plot.
View SolutionThe speed-time graph of a particle moving along a fixed direction is shown in figure. Obtain the distance traversed by the particle between `(a) t =0 s` to `10s. (b) t = 2 s ` to 6s.
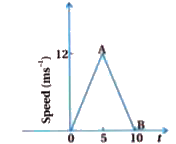
What is the average speed of the particle over the intervals in (a) and (b) ?
View SolutionThe velocity - time graph of a particle in one dimensional motion is shown in figure.
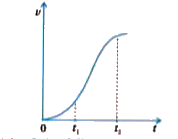
Which of the following formulae are correct for describing the motion of the particle over the time- interval `t _(1)` to `t _(2)` :
(a) `x (t _(2)) = x (t _(1)) +v (t _(2) - t _(1)) + ((1)/(2)) a (t _(2) - t _(1)) ^(2)`
(b) `v (t_(2)) = v (t_(1)) + a (t _(1)))//(t_(2) -t _(1))`
(C) `v _("average")= (x (t _(2)) -x (t _(1)))//(t_(2) -t _(1))`
(d) `a _("average")= (v(t _(2)) - v (t _(1))) //(t_(2) -t _(1))`
(e) `x (t _(2))=x(t_(1)) + v _("average") (t _(2) - t _(1)) + ((1)/(2)) a _("average") (t _(2) -t _(1)) ^(2)`
(f)` c (t _(2)) - c (t _(1)) =` area under the v-t curve bonunded by the t -axis and the dotted line shown.
View SolutionA vehicle travels different distances with different speeds in the same direction. Find the expression for the average speed of a vehicle.
View SolutionA person walking in a straight line, covers half of the distance to be travelled with a speed of `v_(0).` For half of the time, required to complete the remaining distance, he walks with a speed of `v_(1)` and for the remaining half time his speed is `v_(2)` What is the person's average speed during this complete walk ?
View SolutionA motorcyclist covers `1/3` of a given distance with a speed of `10 kmh ^(-1) `, the next `1/3` at `20 kmh ^(-1)` and the last `1/3` at of `30 kmh^(-1).` What is the average speed of the motorcycle for the entire journey ?
View SolutionThe distance between two stations is 40 km. A train takes 1 hour to travel this distance. The train, after starting from first station, moves with constant acceleration for 5 km, then it moves with constant velocity for 20 km and finally its velocity keeps on decreasing continuously for 15 km and it stops at the other station. Find the maximum velocity of the train.
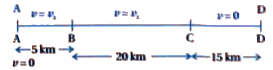
View SolutionA ball thrown in vertically upward direction attains maximum height of 16 m. At what height would its velocity be half of its initial velocity ?
View SolutionThe position of an object, moving in one dimension, is given by the formula `x (t) = (4.2 t ^(2) + 2.6)m.` Calculate its (i) average velocity in the time interval fromj t =0 to t = 3 s and (ii) Instantaneous velocity at ` t=3s.`
`[ (d (x ^(x)))/( dt ) = nx ^(n -1)]`
View SolutionThe position of a particle moving along a straight line is given by `x =2 - 5t + t ^(3).` Find the acceleration of the particle at `t =2 s.` (x is metere).
View SolutionFor a moving paritcle, the relation between time and position is given by `t = Ax ^(2) + Bx.` Where A and B are contants. Find the acceleration of the particle as a function of velocity.
View SolutionTwo cars A and B are at positions 100 m and 200 m from the origin at t = 0. They start simultaneously with constant velocities `10 ms^(-1)` and 5 `ms^(-1)` respectively in the same direction. Calculate the time and position at which they will overtake one another.
View SolutionThe distance between Ahmedabad and Vadodara is 100 km. Two trains set-off simultaneously from Ahmedabad and Vadodara towards each other. The speed of these trains are 45 `kmh^(-1) and 30 kmh^(-1)` respectively. When will they cross each other ?
View SolutionA driver of train A, moving at a speed `30 ms^(-1),` sights another train B going on the same track and in the same direction with speed `10 ms^(-1).` He immediately applies brake that gives his train a constant retardation of `2 ms^(-2).` What must be the minimum distance between trains in order to avoid a collision ?
View SolutionAn object is moving with constant acceleration. Its velocity is `48 ms^(-1)` at the end of 10 second and becomes `68 ms^(-1)` at the end of 15 second. What would be the distance travelled by the object in 15 second ?
View SolutionAn object falling freely covers half of its total distance in last second, then find total height and total times g = 9.8 `ms^(-2).`
View SolutionA stone is fallen freely from a tower and after n seconds another stone is thrown upwards with u m/s, then at what distance from top of tower second stone will overtake first stone ?
View SolutionA train is moving with constant acceleration. When the ends of a train pass by a signal their speeds are u and v respectively. Calculate the speed of the midpoint of the train while passing the signal.
View Solution
SECTION-B questions and complete solutions for chapter MOTION IN A STRAIGHT LINE of KUMAR PRAKASHAN KENDRA PHYSICS (GUJRATI ENGLISH) of Class 11