Question

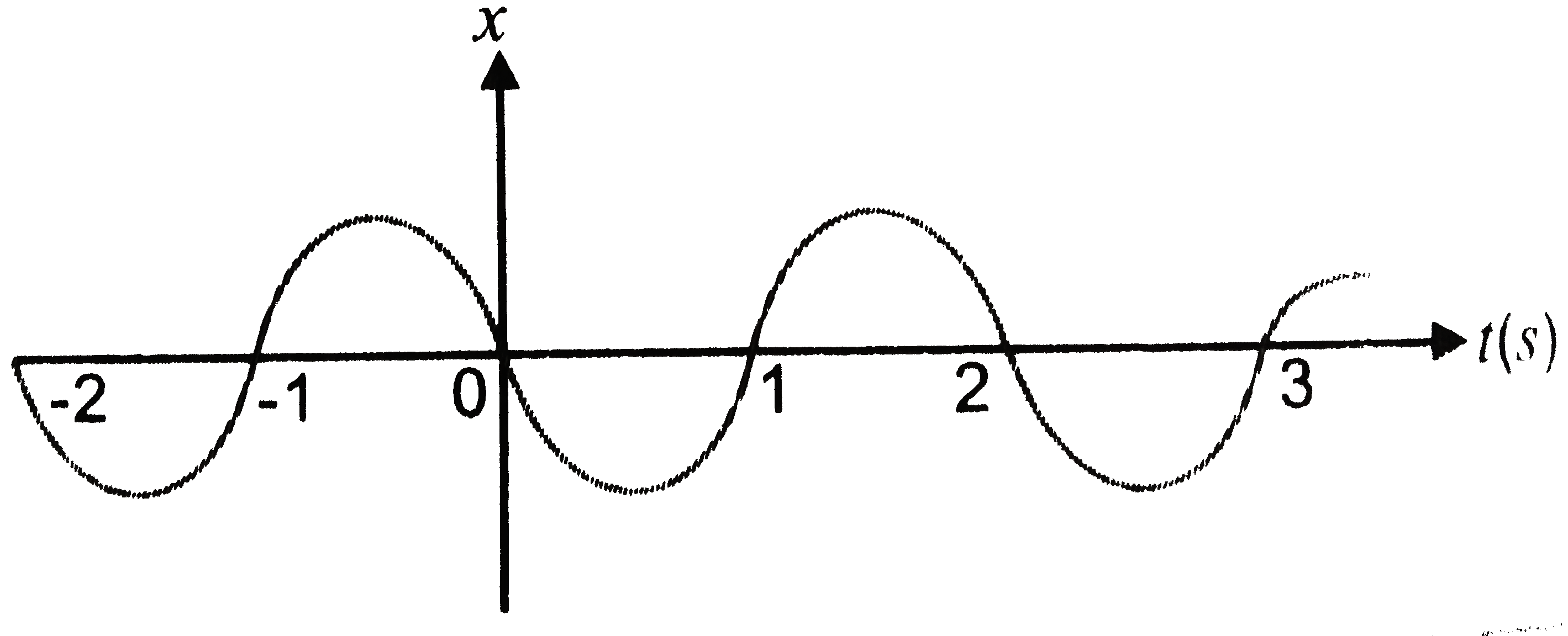
Figure gives the ${\displaystyle x\to t}$ plot of a particle executing one-dimensional simple harmonic motion. (you will learn about this motion inmore detail in Chapter 14). Give the signs of position, velocity and acceleration variables of the particle at ${\displaystyle t=0.3s,1.2s,-1.2s.}$

Explanation

We know that for object performing simple harmonic motion, acceleration,
`a =- omega ^(2) x " "..(1)`
where `omega=` angular frequency = constant
velocity `v = (dx)/(dt) " "…(2)`
(i) Graph at t = 0.3 shows that x is in negative direction, (x `lt` 0), slope is also negative hence velocity is negative (v `lt` 0), then also ma = - kx, hence acceleration is positive (a `gt` 0).
(ii) x is positive at t = 1.2 s, slope of graph is positive (v `gt` 0) where according to equation (1) acceleration is negative (a < 0).
(iii) Position is negative at t= -1.2 s (x `lt` 0), slope is negative so by equation (2) velocity is positive. (v `gt` 0) and again by ma = - kx a is positive (a `gt` 0).