Complete Solutions to EX -13.1 of chapter LIMITS AND DERIVATIVES of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | LIMITS AND DERIVATIVES |
| NAGEEN PRAKASHAN | EX -13.1 |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
`lim_(xrarr3) x+3`
View Solution`lim(xrarrpi)(x-(22)/(7))`
View Solution`lim_( r to 0) pir^(2)`
View Solution`lim_(xrarr4) (4x+3)/(x-2)`
View Solution`lim_(xrarr-1) (x^(10)+x^(5)+1)/(x-1)`
View Solution`lim_(xrarr0) ((x+1)^(5)-1)/(x)`
View Solution`lim_(xrarr2) (3x^(2)-x-10)/(x^(2)-4)`
View Solution`lim_(xrarr3) (x^(4)-81)/(2x^(2)-5x- 3) `
View Solution`lim_(xrarr0) (ax+b)/(cx+1)`
View Solution` lim_(z to 1) (2^(1//3)-1)/(z^(1//6)-1)`
View Solution`lim_(xrarr1) (ax^(2)+bx+c)/(cx^(2)+bx+a)a+b+cne0`
View Solution`lim_(xrarr-2)((1)/(x)+(1)/(2))/(x+2)`
View Solution`lim_(xrarr0) (sinax)/(bx)`
View Solution`lim_(xrarr0) (sinax)/(sinbx),a,bne0`
View Solution`lim_(xrarrpi) (sin(pi-x))/(pi(pi-x))`
View Solution`lim_(x to 0) (cos x)/(pi-x)`
View Solution`lim_(xrarr0)(cos 2x-1)/(cosx-1)`
View Solution`lim_(xrarr0) (ax+x cos x)/(b sinx)`
View Solution`lim_(xrarr0) x sec x`
View Solution`lim_(xrarr0) (sinax+bx)/(ax+si nbx),a,b,a+bne0`
View Solution`lim_(xrarr0) ("cosec "x-cotx)`
View Solution`lim_( x to (pi/(2)) (tan2x)/(x-(pi)/(2))`
View SolutionFind `lim_(xrarr0) f(x)` and `underset(xrarr1)f(x)`.
`f(x)={{:(2x+3,xle0),(3(x+1),xgt0):}`
View SolutionFind `lim_(x to 1) f(x)`, where
`f(x)={{:(x^(2)-1,xle1),(-x^(2)-1,xgt1):}`
View SolutionEvaluate `lim_(xrarr0) f(x)`, where
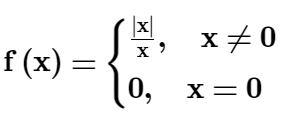
View SolutionFind `lim_(xrarr0) f(x)` where
`f(x){{:((x)/(|x|),xne0),(0,x=0):}`
View SolutionFind `lim_(xrarr5) f(x)`, where `f(x)=|x|-5`.
View SolutionSuppose `f(x)={{:(a+bx,xlt1),(4,x=1),(b-ax,xgt1):}`
and if `lim_(xrarr1) f(x)=f(1)` what are possible values of a and b ?
View SolutionLet `a_(1),a_(2),.......,a_(n)` be fixed real numbers and define a function `f(x)=(x-a_(1))(x-a_(2)) ......(x-a_(n))`, what is lim `f(x)`? For some `anea_(1),a_(2),.........a_(n)`, compute `lim_(Xrarr1) ` f(x)
View SolutionIf ` f(x)={{:(|x|+1,xlt0),(0,x=0) ,(|x|-1,xgt0):}`
for what value (s) of a does `lim_(xrarra) f(x)` exists?
View SolutionIf the function f(x) satisfies `lim_(xrarr1) (f(x)-2)/(x^(2)-1)=pi`, evaluate `lim_(Xrarr1) f(x)`.
View SolutionIf `f(x)= {{:(mx^(2)+n,xlt0),(nx+m,0ltxle1),( nx^(3)+m,xgt1):}`
For what integers m and n does both `lim_(xrarr0) f(x)` and `lim_(xrarr1) f(x)` exist?
View Solution
EX -13.1 questions and complete solutions for chapter LIMITS AND DERIVATIVES of NAGEEN MATHS (HINGLISH) of Class 11