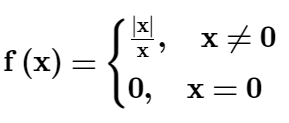Find limx→0f(x) where
f(x){x|x|x≠00x=0
Video Solution
Text Solution
f(x){x|x|x≠00x=0
at x=0
LHL limx→0−f(x)
=limh→0f(0−h)
=hh→0|−h|
=limh→0h−h=limh→0(−1)=−1
Let 0−h=x
⇒0−h→0
⇒h→0
RHL=limX→0+f(x)
limh→0f(0+h)
=limh→0h|h|
=limh→0hh=1h→0=1
∵LHLneRHL
∴limx→0 f(x) does not exist.
Let 0+h=x
⇒0+h→0
⇒h→0
|
Topper's Solved these Questions
- LIMITS AND DERIVATIVESBook:NAGEEN PRAKASHANChapter:LIMITS AND DERIVATIVESExercise:EX -13.2
Explore 11 Videos
- LIMITS AND DERIVATIVESBook:NAGEEN PRAKASHANChapter:LIMITS AND DERIVATIVESExercise:Miscellaneous Exercise
Explore 30 Videos
- LIMITS AND DERIVATIVESBook:NAGEEN PRAKASHANChapter:LIMITS AND DERIVATIVESExercise:EX-13H
Explore 9 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBook:NAGEEN PRAKASHANChapter:INTRODUCTION OF THREE DIMENSIONAL GEOMETRYExercise:Miscellaneous Exercise
Explore 6 Videos
- LINEAR INEQUALITIESBook:NAGEEN PRAKASHANChapter:LINEAR INEQUALITIESExercise:MISCELLANEOUS EXERCISE
Explore 14 Videos
Similar Questions
Knowledge Check
f(x)={|x|cos(1x)x≠00x=0 is
Adiscontinuous at x=0Bcontinuous at x=0Cdoes not existDNone of the abovef(x)={x2x2+|x|x≠01x=0then f(x) is
Acontinuous but non- differentiable at x=0Bdifferentiable at x=0Cdiscontinuous at x=0Dnone of thesef(x)={(2−Sin(1x))|x|x≠00x=0
AMonotonic in (−∞,0)∪(0,∞)BNot Monotonic in (−∞,0)∪(0,∞)CMonotonic in (−∞,∞)DNot Monotonic in (−∞,∞)