Find limx→0f(x) and f(x)x→1.
f(x)={2x+3x≤03(x+1)x>0
Text Solution
f(x)={2x+3x≤03(x+1)x>0
at x=0
LHL=limx→0−f(x)
=limh→0f(0−h)
Let 0−h=x
⇒0−h→0
⇒h→0
limh→02(0−h)+3=2(0)+3=3
RHL=f(x)x→0+
=limh→0f(0+h)
=limh→03(0+h+1)
=3(0+1)=3
∵LHL=RHL=3
∴limx→0f(x)=3
at x=1
LHL=limx→11−f(x)
=limh→0f(1−h)
=limh→03(1−h+1)
=3(2−0)=6
RHL=limx→1+f(x)
=limh→0f(1+h)
=limh→03(1+h+1)
=3(2+0)=6
∵LHL=RHL=6
∴limx→1f(x)=6
Let 1+h=x
⇒1+h→1
⇒h→0
|
Topper's Solved these Questions
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EX -13.2
11 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise
30 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EX-13H
9 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Miscellaneous Exercise
6 Videos
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR INEQUALITIESEXERCISE - MISCELLANEOUS EXERCISE
14 Videos
Similar Questions
Knowledge Check
A function is defined as f(x)={ex,x≤0|x−1|,x>0, then f(x) is
Af(x) is differentiable at x=0Bf(x) is continuous at x = 0 ,1Cf(x) is differentiable at x=1DNone of the aboveIf f(x)={(sin(x2−3x),x≤0
.x+5x2,x>0Af(x) has a local minimaBf(x) has a local maximaCf(x) has point of inflectionDnone of theseIf limx→0f(x)x2=aandlimx→0f(1−cosx)g(x)sin2x=b (where b≠0),
then limx→0g(1−cos2x)x4 isA4abBa4bCabDnone of these
Evaluate limx→0f(x), where
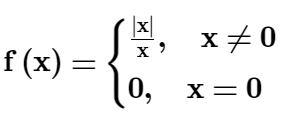
View SolutionFind limx→0f(x) where
f(x)={x|x|x≠00x=0
View SolutionLet f:R→R be a function satisfying Limx→0+f(x)=2, Limx→0−f(x)=3 and f(0)=4 The value of Limx→0f(x3−x2)Limx→0f(2x4−x5)=
View SolutionIf f(x)={xnsin(1x2)x≠00x=0, (n∈I), then (a) limx→0f(x) exists for n>1 (b) limx→0f(x) exists for n<0 (c) limx→0f(x) does not exist for any value of n (d) limx→0f(x) cannot be determined
View SolutionIf f(x)={xnsin(1x2)x≠00x=0, (n∈I), then (a) limx→0f(x) exists for n>1 (b) limx→0f(x) exists for n<0 (c) limx→0f(x) does not exist for any value of n (d) limx→0f(x) cannot be determined
View Solution
