Complete Solutions to LEVEL- (C.W) of chapter TRANSMISSION OF HEAT of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | TRANSMISSION OF HEAT |
| NARAYANA | LEVEL- (C.W) |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
Three rods of material 'x' and three rods of materialy are connected as shown in All the rods are of identical length and cross section If the end `A` is maintained at `60^(@)C` and the junction `E` at `10^(@0C` find effective Thermal Resistance Given length of each rod =1 area of cross-section =A conductivity of x=K and conductivity of `y =2K`
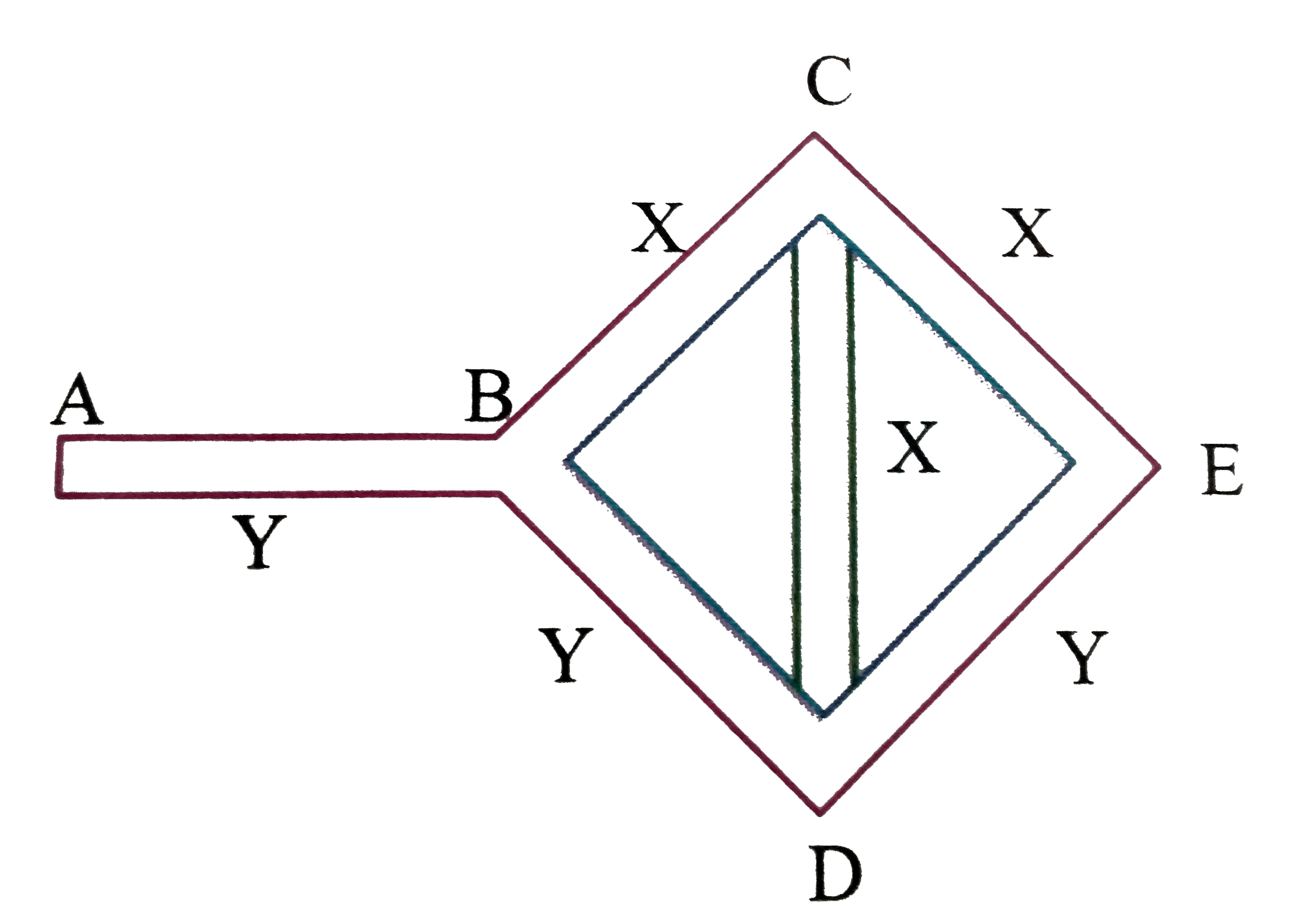 .
.
View SolutionA cylinder of radius `R` made of a material of thermal conductivity `K_(1)` is surrounded by cylindrical shell of inner radius `R` and outer radius `2R` made of a material of thermal con-ductivity `K_(2)` The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .
.
View SolutionWater is being boiled in a flat bottomed kettle placed on a stove The area of the bottom is `300cm^(2)` and the thickness is `2mm` If the amount pf steam produced is `1gm min^(-1)` then the difference of the temperature between the inner and the outer surface of the bottom is (thermal conductivity of the matrial of the kettle `0.5calcm^(-1)C^(-1)` latent heat of the steam is equal to `540calg^(-1))` .
View SolutionA point source of heat of power P is placed at the centre of a spherical shell of mean radius R. The material of the shell has thermal conductivity K. If the temperature difference between the outer and inner surface of the shell in not to exceed T, the thickness of the shell should not be less than .......
View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x, respectively, are `T_2 and T_1(T_1gtT_1)`. The rate of heat transfer through the slab, in a steady state is `((A(T_2-T_1)K)/2)f`, with f equal to

View Solution`A` and `B` are two points on uniform metal ring whose centre is `O` The angle `AOB =theta` A and `B` are maintaind at two different constant temperatures When `theta =180^(@)` the rate of total heat flow from `A` to `B` is `1.2W` When `theta =90^(@)` this rate will be .
View SolutionTwo ends of a conducting rod of varying cross-section are maintained at `200^(@)C` and `0^(@)C` respectively. In steady state:

View Solution
Three rods of same dimensions are arranged as shown in Fig. They have thermal conductivities `K_1`,`K_2` and `K_3`. The points P and Q are maintained at different temeperature for the heat to flow at the same rate along PRQ and PQ. Whi of the following options correct?
View SolutionA boiler is made of a copper plate `2.4mm` thick with an inside coating of a `0.2mm` thick layer of tin The surface area exposed to gases at `700^(@)C` is `400cm^(2)` The maximum amount of steam that could be generated per hour at atmospheric pressure is
`({:(K_(cu)=0.9cal//cm-s-^(0)& k_("tin")=0.15cal//cm-s-^(0)C andL_(steam)=540cal//g:})` .
View SolutionIce starts forming in lake with water at `0^(@)C` and when the atmospheric temperature is `-10^(@)C`. If the time taken for `1 cm` of ice be `7` hours. Find the time taken for the thickness of ice to change from `1 cm` to `2 cm`
View SolutionA long metallic bar is carrying heat from one of its ends to the other end under steady-state. The variation of temperature `theta` along the length x of the bar from its hot end is best described by which of the following figures?
View SolutionThe temperature drop through each layer of a two layer furnace wall is shown in Assume that the external temperature `T_(10` and `T_(3)` are mainitained constant and `T_(1)gtT_(3)` If the thichness of the layers `x_(1)` and `x_(2)` are the same which of the following statements are correct
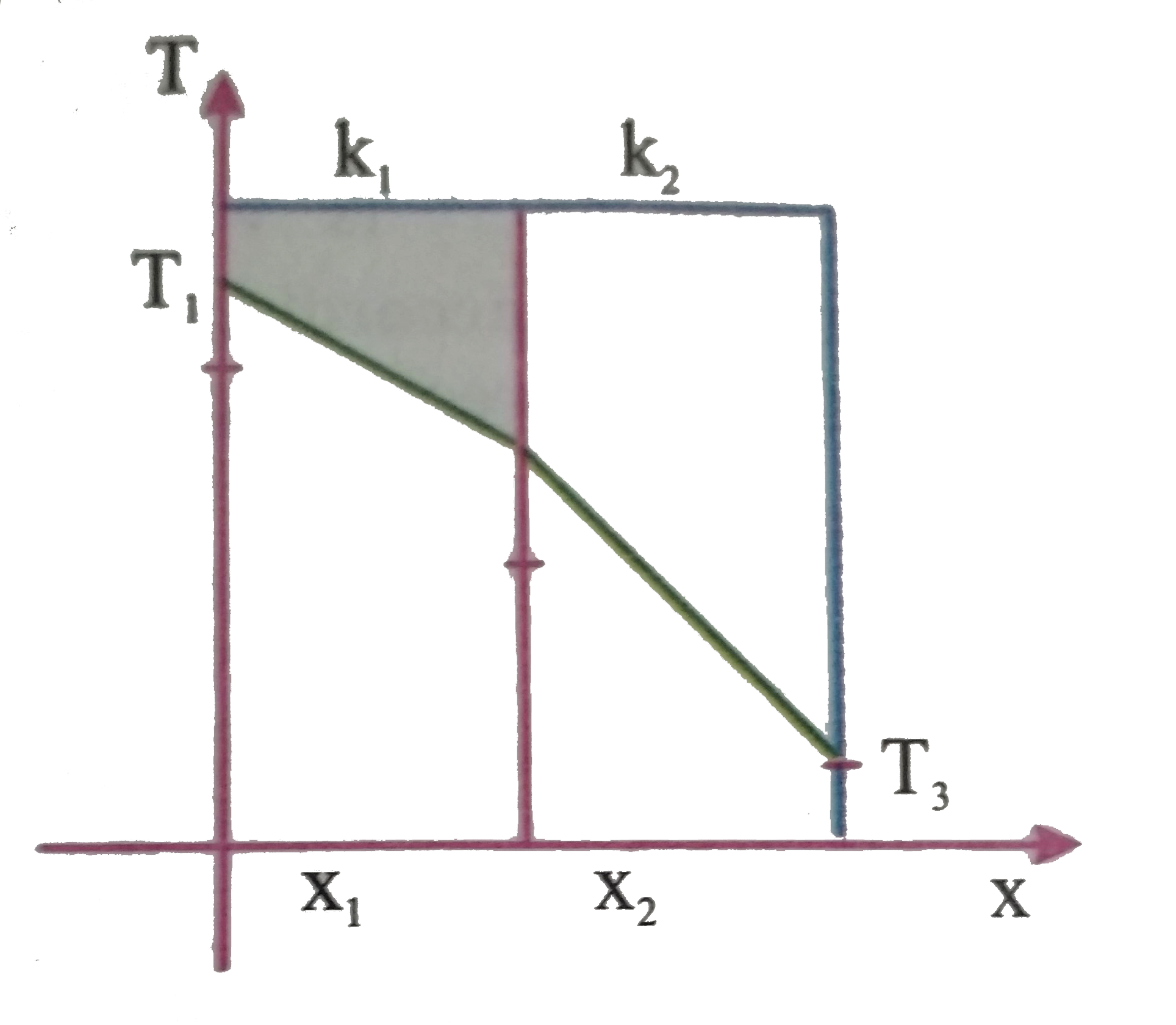 .
.
View SolutionThe wall with a cavity consists of two layers of brick separated by a layer of air All three lay-ers have the same thickness and the thermal conductivity of the brick is much greater than that of air The left layer is at a higher temperature than the tight layer and steady state condition exists Which of the following graphs perdicts correctly the variation of temperature `T` with distance d inside the cavity ?.
View SolutionA ring consisting of two parts `ADB` and `ACB` of same conductivity k carries an amount of heat `H` The `ADB` part is now replaced with another metal keeping the temperature `T_91)` and `T_(2)` constant The heat carried increases to `2H` What should be the conductivity of the new `ADB` Given `(ACB)/(ADB)=3`
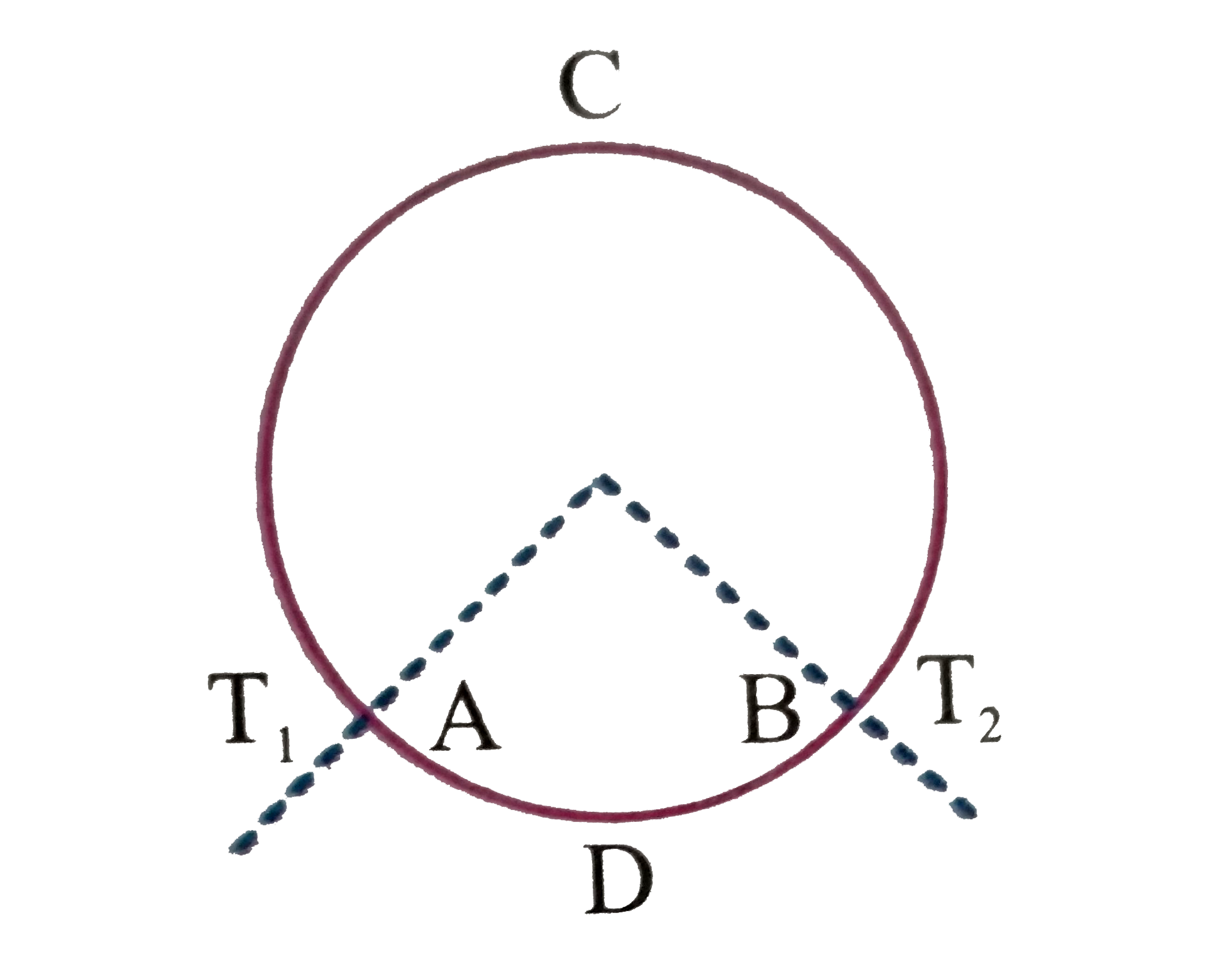 .
.
View SolutionTwo metallic spheres `S_1 and S_2` are made of the same material and have got identical surface finish. The mass of `S_1` is thrice that of `S_2`. Both the spheres are heated to the same high temperature and placed in the same room having lower temperature but are thermally insulated from each other. the ratio of the initial rate of cooling of `S_1` to that of `S_2` is
`(a)1/3 (b)1/(sqrt3) (c) (sqrt3)/1 (d) (1/3)^(1/3)`
View SolutionThe temperature of an spherical isolated black body falls from `T_(1)` and `T_(2)` in time t them time t is
View SolutionA star behaves like a perfectly black body emitting radiant energy The ratio of radiant energy per second by this star to that emitted by another star having 8 times the radius of former, but having temperature, one-fourth that of the former in Kelvin is .
View SolutionA sphere of density 'd' specific heat capacity 'c' and radius 'r' is hung by athermally insulating thread in an enclosure which is kept at lower temperature than the shpere The temperature of the sphere starts to drop at rate which is proportional to .
View SolutionAssuming the Sun to be a spherical body of radius R at a temperature of TK, evaluate the total radiant powered incident of Earth at a distance r from the sun
where `r_0` is the radius of the Earth and `sigma` is Stefan's constant.
View SolutionThe spectral emissive power `E_(lambda)` for a body at temperature `T_(1)` is poltted againist the wavelenght and area under the curve is found to be `A.At` a different temperature `T_(2)` the area is found to be A then `lambda_(1)//lambda_(2)=`
 .
.
View SolutionA heated object (at time `t=0` and temperature `T=T_(0))` is taken out of the oven to cool and placed on a table near an open window Write an expression for its temperature as function of time `T` where `T_(s)` is the surrounding temperature .
View SolutionA system `S` receives heat continuously from an electric heater of power `10 W`. The temperature of `S` becomes constant at `50^(@)C` when the surrounding temperature is `20^(@)C`. After the heater is switched off, `S` cools from `35.1^(@)C` to `34.9^(@)C` in `1 minute`. the heat capacity of `S` is
View SolutionAccording to Newton's law of cooling, the rate of cooling of a body is proportional to `(Delta theta)^n`, where `Delta theta` is the difference of the temperature of the body and the surroundings, and n is equal to
View SolutionA liquid in a beaker has temperature `theta(t)` at time t and `theta_0` is temperature of surroundings, then according to Newton's law of cooling the correct graph between `log_e( theta-theta_0)` and t is :
View SolutionIf a piece of metal is heated to temperature `theta` and the allowed to cool in a room which is at temperature `theta_0`, the graph between the temperature T of the metal and time t will be closet to
View Solution
LEVEL- (C.W) questions and complete solutions for chapter TRANSMISSION OF HEAT of NARAYANA PHYSICS (HINGLISH) of Class 11