Complete Solutions to Solved Example of chapter TRANSMISSION OF HEAT of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | TRANSMISSION OF HEAT |
| NARAYANA | Solved Example |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
The temperature of the two ends `A` and `B` of a rod of length `25cm` and circular cross section are `100^(@)C` and `0^(@)C` respectively In the steady state, find the temperature at a point `10cm` from the end `B` (ifnore loss of heat from curved surface of the body) ?
View SolutionTwo walls of thicknes `l_(1)` and `l_(2)` and ther-mal condctivities `K_(1)` and `K_(2)` are in contact In the steady state, if the temperature at the outer faces are `T_(1)` and `T_(2)` find the temperature at the common wall .
View SolutionA rod of length `L` with sides fully insulated is made of a material whose thermal conductivity `K` varies with temperature as `K=(alpha)/(T)` where `alpha` is constant. The ends of rod are at temperature `T_(1)` and `T_(2)(T_(2)gtT_(1))` Find the rate of heat flow per unit area of rod .
View SolutionA cubical thermocol ice box of side length `30cm` has thichess of `5.0cm` If `4.0kg` of ice is put in the box estimate the amount of ice remaining after `6hr` The utside temperature is `45^(@)C` and co-efficinet of the thermal conductivity of the thermocol is `0.01 J s^(-1) m^(-1) K^(1)` (Latent Heat of fusion of water `=335 xx 10^(3) Jkg^(-1))` .
View SolutionA metal rod `AB` of length `10x` has it one end in ice at `0^(@)C` and the other end `B` in water at `100^(@)C` If a point `P` on the rod is maintained at `400^(@)C` then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of melting of ice is `80cal//g` If the point `P` is at a distance of `lambdax` from the ice end A find the value of `lambda` [neglect any heat loss to the surrounding] .
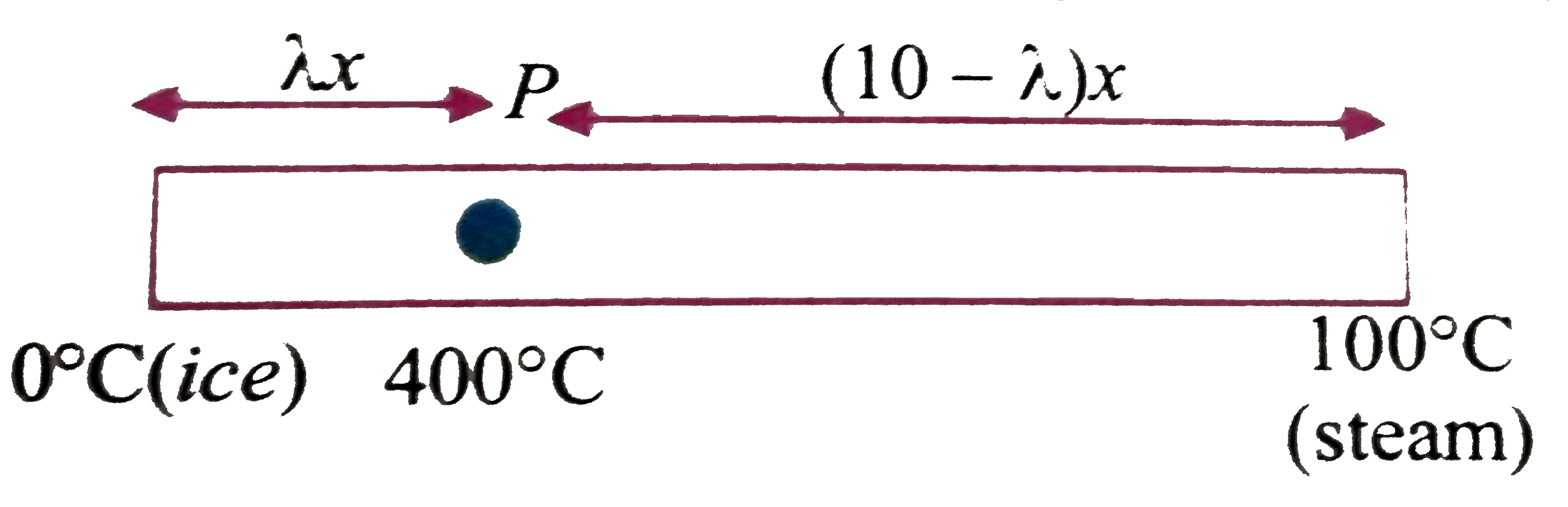 .
.
View SolutionFind the value of the thermal resistance of the non-uniform cylindrical rod of thermal conductivity `K` and length I as shown in
 .
.
View SolutionA room has a window fixed with a pane of area `1.2m^(s)` The glass has thickness `2.2mm` If the temperature outside the room is `36^(@)C` and the temperature inside is `26^(@)C`
(a) calculate the heat flowing into the room every hour
(b) If the same single pane window is replaced by double paned window with an air gap of `0.50cm` between the two panes calculate the heat flowing into the room every hour
`K_(g) =0.80 Wm^(-1)K^(-1),K_(air)=0.0234Wm^(-1)K^(-1)` .
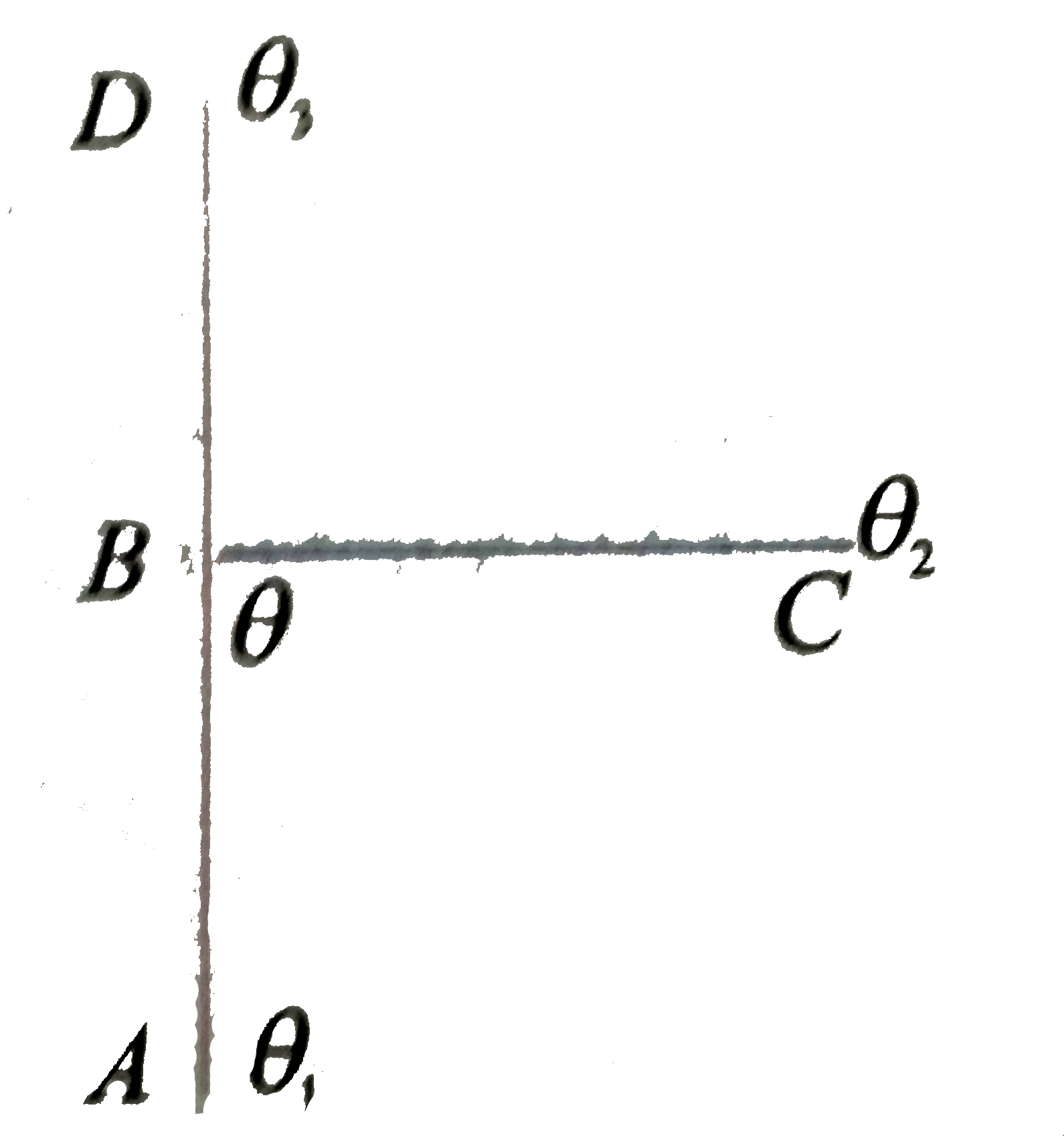
View SolutionThree rods `AB,BC` and `BD` made of the same materical and having the same area of cross section have been joined as shown is the The ends `A,C` and `D` are held at temperatures `20^(@)C` Cand `80^(@)C` respectively If each rod is of same length then find the temperature at the junction `B` of the three rods
 .
.
View SolutionThree rods of Copper Branss and Steel are welded together to form a Y-shaped structure Area of cross -section of each rod is `4cm^(-2)` End of copper rod is maintained at `100^(@)C`, where as ends of brass, steel are kept at `0^(@)C` Lenths of the copper brass and steel rods are `46,13` andd `12cms` respectively The rods are thermally insulated from surroundings except at ends Thermal conductivities of copper, brass and steel are `0.92,0.26` and `0.12 CGS` units respectively Rate of heat flow through coper rod is .
View SolutionA cylinder of radius `R` made of a material of thermal conductivity `K_(1)` is surrounded by cylindrical shell of inner radius `R` and outer radius `2R` made of a material of thermal con-ductivity `K_(2)` The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .
.
View SolutionTwo plates each of area `A` thickness `L_(1)` and `L_(2)` thermal conductivities `K_(1)` and `K_(2)` respectively are joined to from a single plate of thickness `(L_(1)+L_(2))` If the temperatures of the free surfaces are `theta_(1)` and `theta_(2)` Calculate
(a) Rate of flow of heat
(b) Temperature of interface
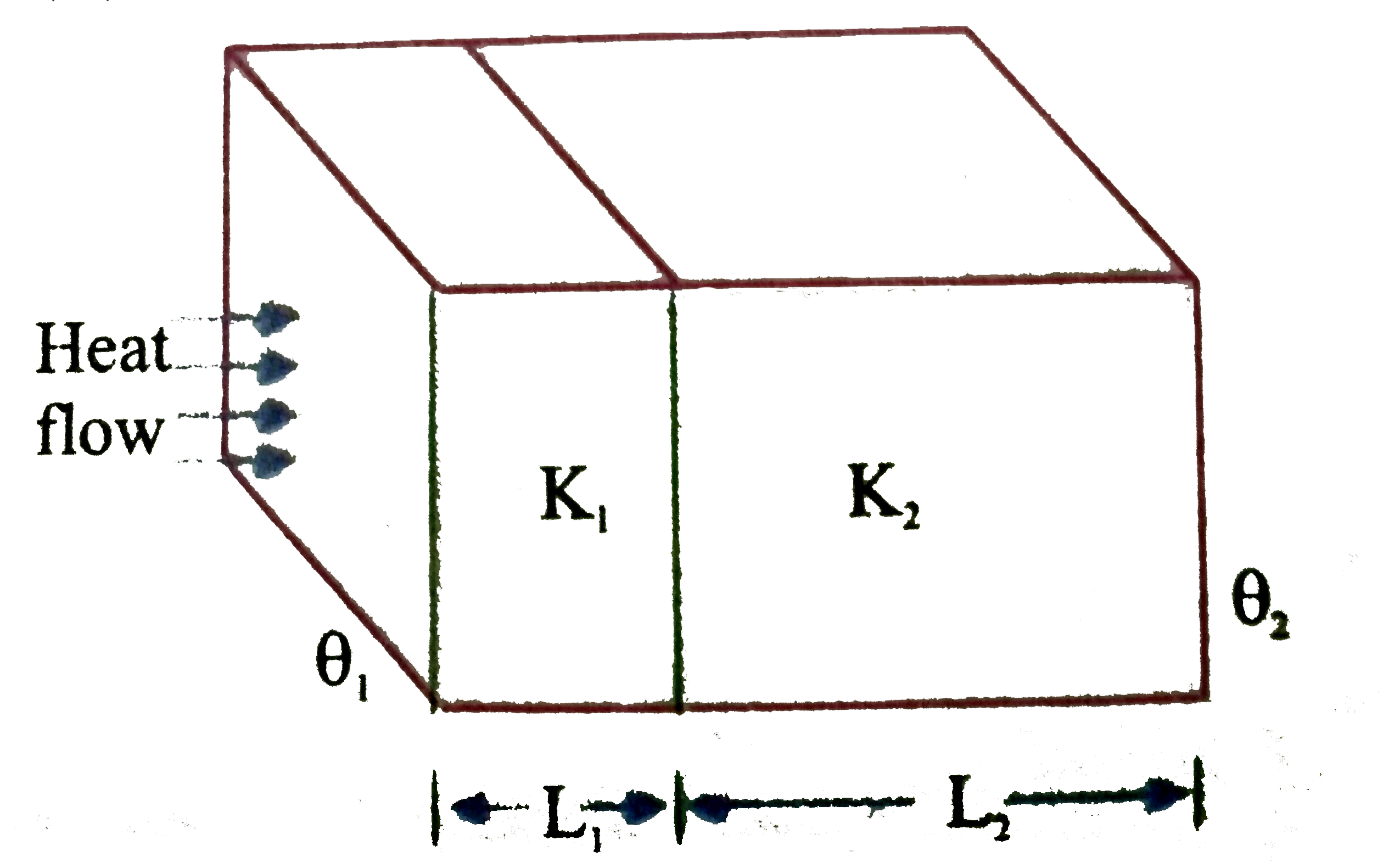 .
.
View SolutionRods `X` and `Y` of identical dimensions but of different materials are joined as shown in The length of each part is the same It the temperature of end `A` and `F` be main tained at `100^(@)C` and `20^(@)C` respectively then find the temperatures of the junctions `B` and `E` (Thermal conductivity of `X` is double that of `Y`) .
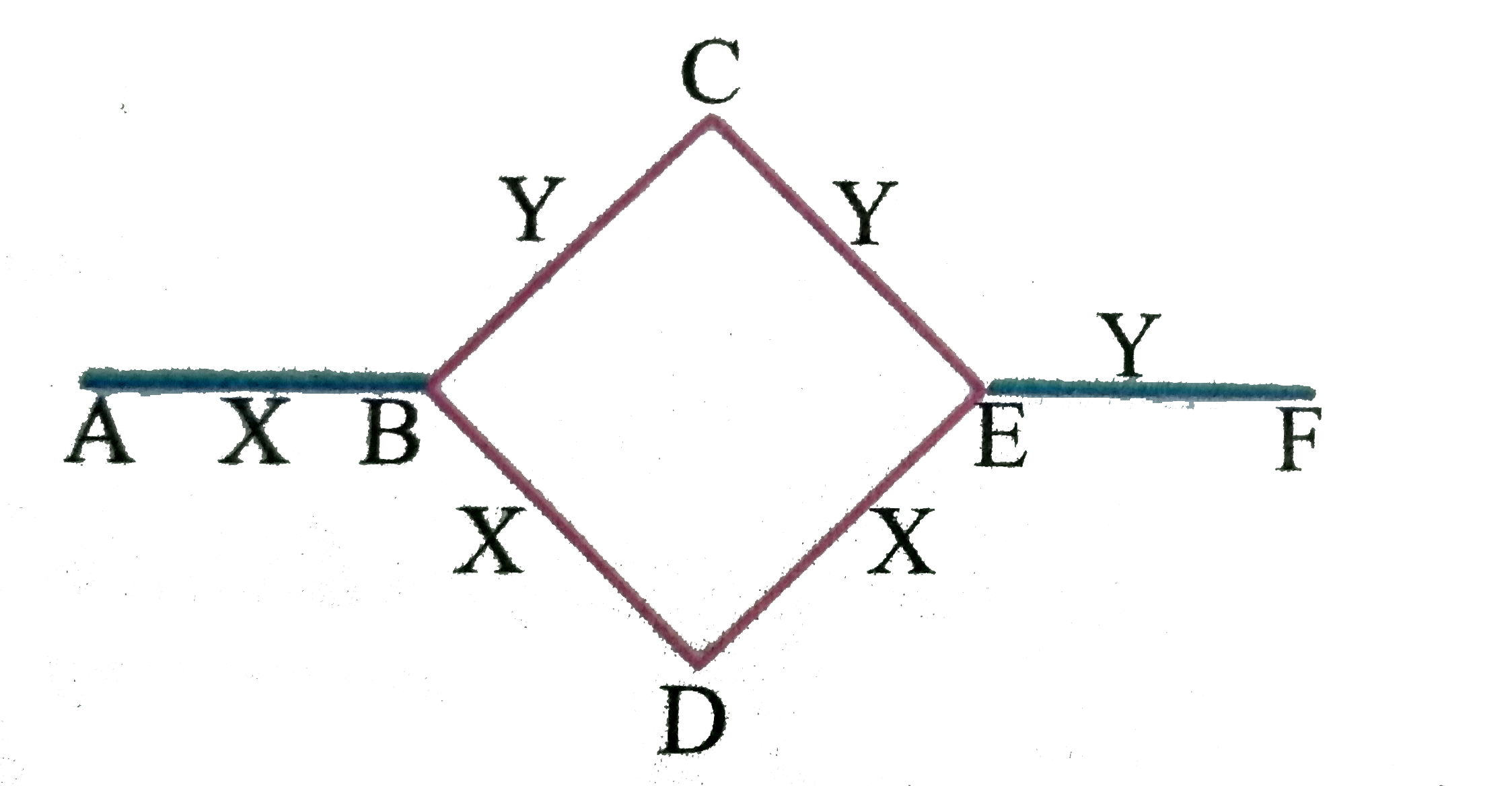
View SolutionThree rods `AB,BC`and `BD` having thremal conductivities in the ratio `1:2:3` and lengths in the ratio `2:1:1` are joined as shown in The ends `A,C` and `D` are at temperature `theta_(1),theta_(2)` and `theta_(3)` respectively Find the temperature of the junction `B`
(Assume steady state and `theta_(1)gt theta gt theta_(2)gttheta_(3))`
 .
.
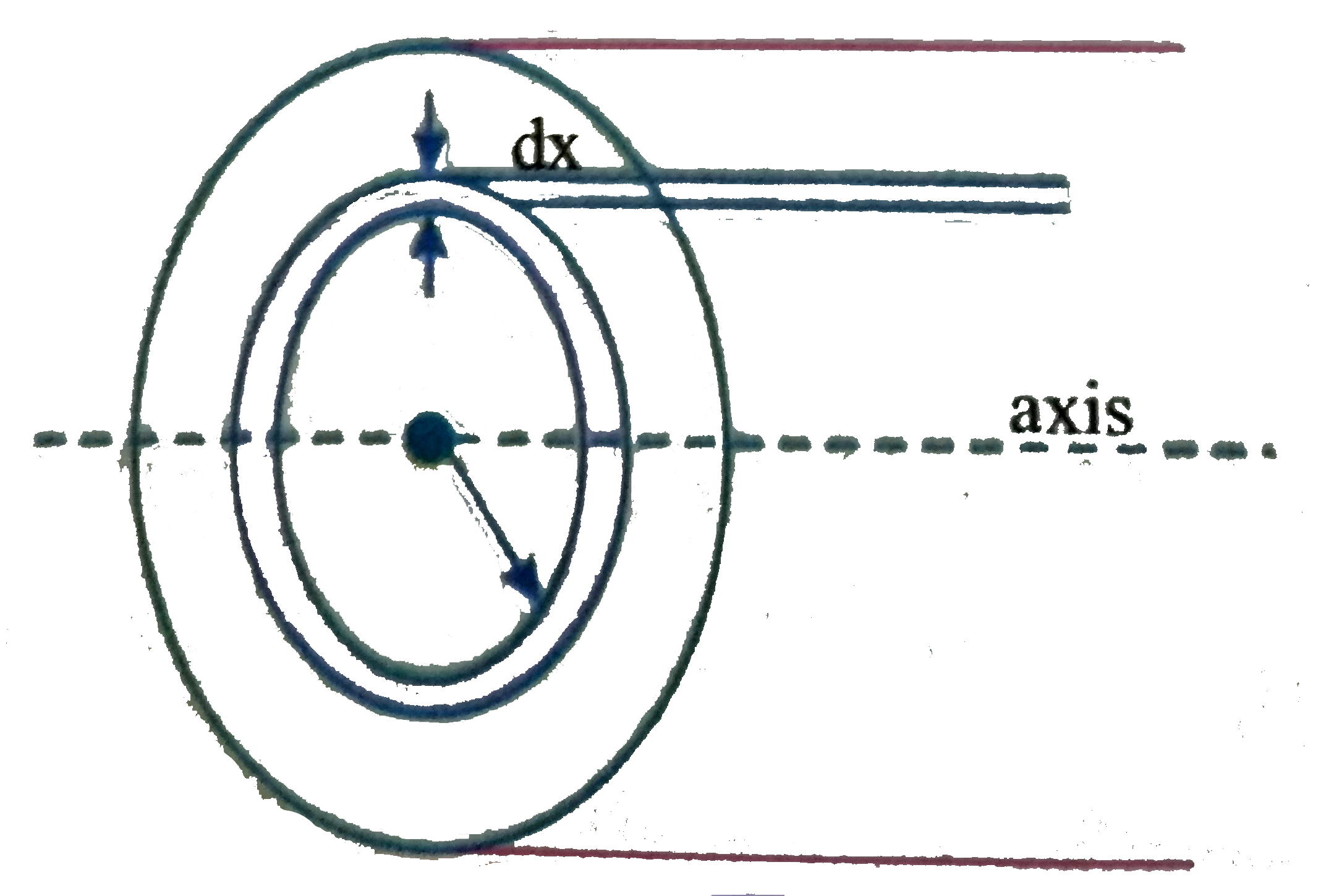
View SolutionA cylinder of radius `R` and length l is made uo of a substnace whose thermal conductivity `K` varies with the distance x from the axis as `K=K_(1)x+K_(2)` Detemine the effective thermal conductivity between the flat faces of the cylinder
 .
.
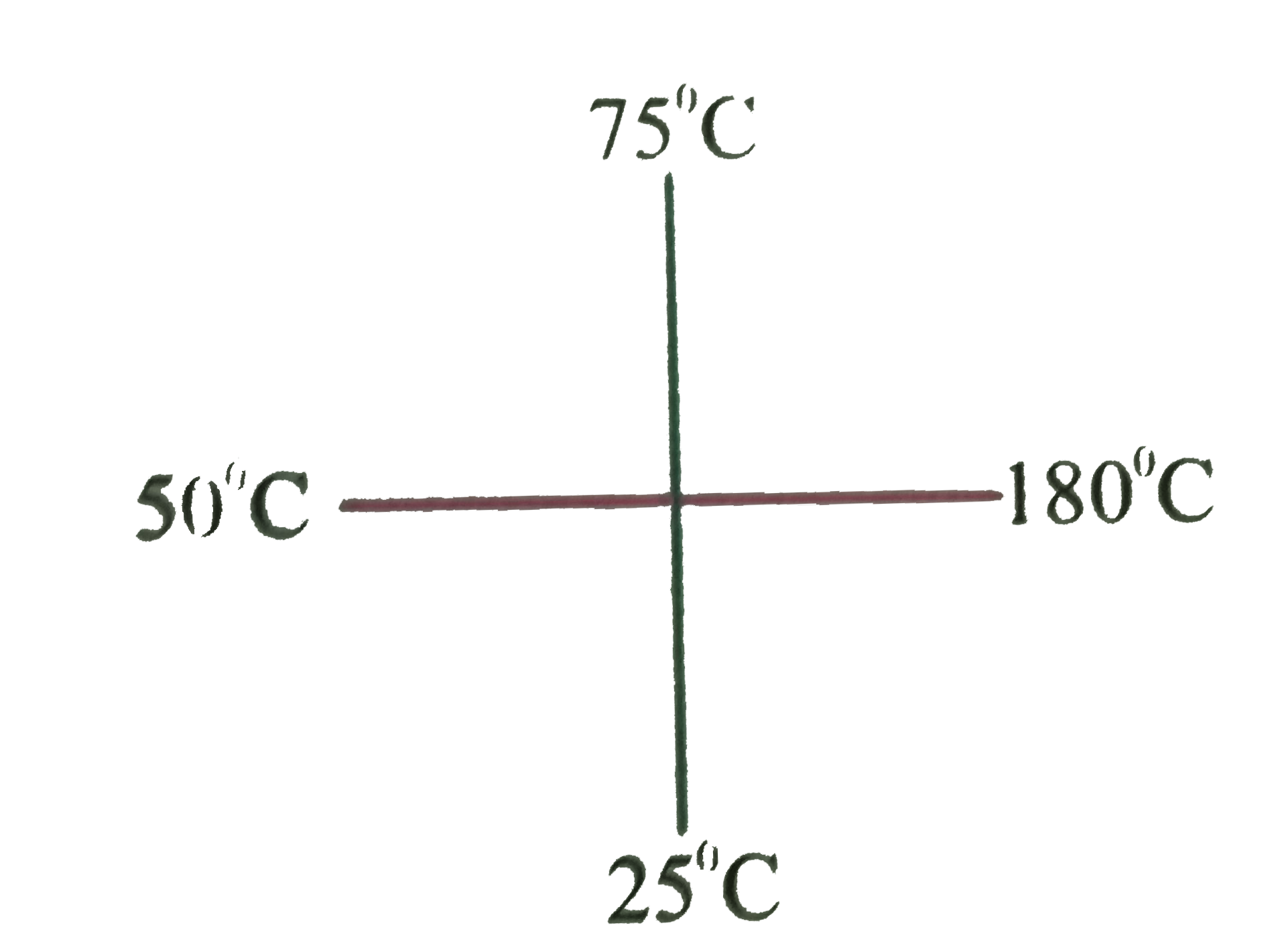
View SolutionTwo identical rods are joined at their middle points The ends are maintained at constant temperatures as indicated Find the temperature of the junction
 .
.
View SolutionThe thickness of ice in a lake is `5cm` and the atmospheric temperature is `10^(@)C` Calculate the time rquired for the thickness of ice to grow to `7cm` Therml conductivity for ice `=4 xx 10^(-3) cal cm^(-1) s^(-1) c^(-10` density of ice `=0.92 g //cm^(3)` and latent heat of fusion of ice `=80 cal//g` .
View SolutionA hollow sphere of glass whose external and internal radii are `11cm` and `9cm` respec-tively is completely filled with ice at `0^(@)C` and placed in a both of boiling water How long will it take for the ice to melt completely ? Givne that density of ice `=0.9g//cm^(3)` latent heat of fusion of ice `=80 cal//g` and thermal conductivity of glass `=0.002 cal//cm-s^(@)C` .
View SolutionIn the Ingen hausz method to compare the thermal conductivities of differnet substances the length upto which wax melted in copper and zinc rods are `9.3 cm` and `5cm` respectively Compare their thermal conductivities .
View SolutionA stema pipe with a radius `R_(1)` is surrounded by an insulating jacket with an outer radius of `R_(0)` If the temperature of the inner `(theta_(1))` and outer `(theta_(0))` surface are fixed `(theta_(1) gt theta_(0))` find the heat flow through the jacket. (Apply the heat conduction euation to steady state radial heat flow corresponding to cylindrical symmetry) .
View SolutionA steam pipe of radius `5cm` carries steam at `100^(@)C` The pipe is covered by a jacket of insulating material `2cm` thick having a ther mal conductivity `0.07Wm^(-1) k^(-1)` if the tempera ture at the outer wall of the pipe jacket is `20^(@)C` how much heat is lost through the jacket per mater lenght in an hour ? .
View SolutionA trunner moves along the road at `2ms^(-1)` in still air that is at a temperature of `29^(@)C` His surface area is `1.4m^(2)` of which apporoximately `85%` is exposed to the air Find the rate of convective heat loss from his skin at a temperature `35^(@)C` to the outside air ? Coefficient of convection for dry air and bare skin at whind speed `2ms^(-1)` is `22W//m^(2)-C` .
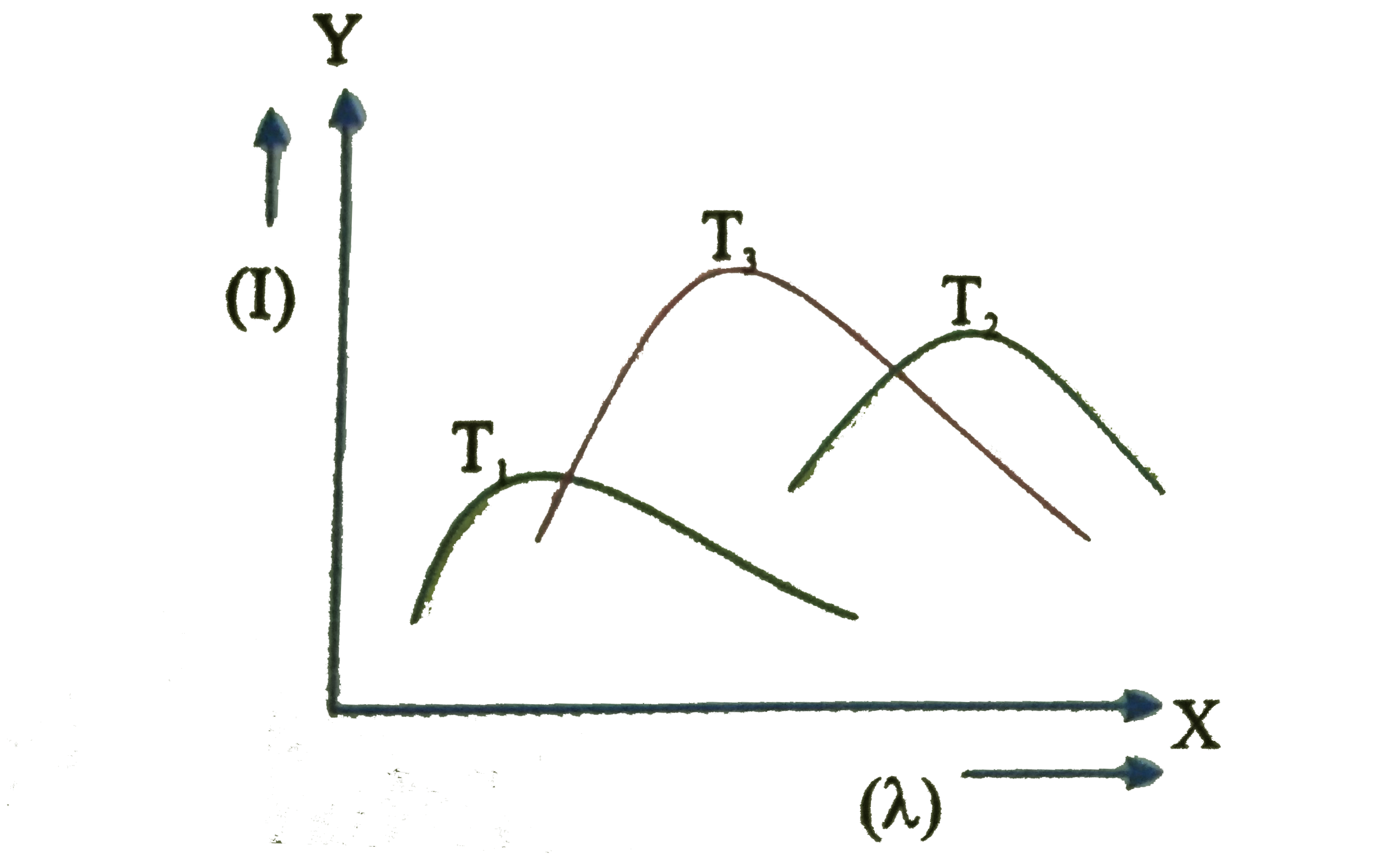
View SolutionThe plots of intensity versus wavelength for three black bodies at temperatures `T_(1),T_(2)` and `T_(3)` respectively are shown in Their temperatures are shown in How their temperatures are related ?
 .
.
View SolutionVariation of radiant energy emitted by Sun, filament of Tungsten Lamp and welding arc as a function of its wavelength shown in Identify the temperatures of Sun. filament lamp and welding are
 .
.
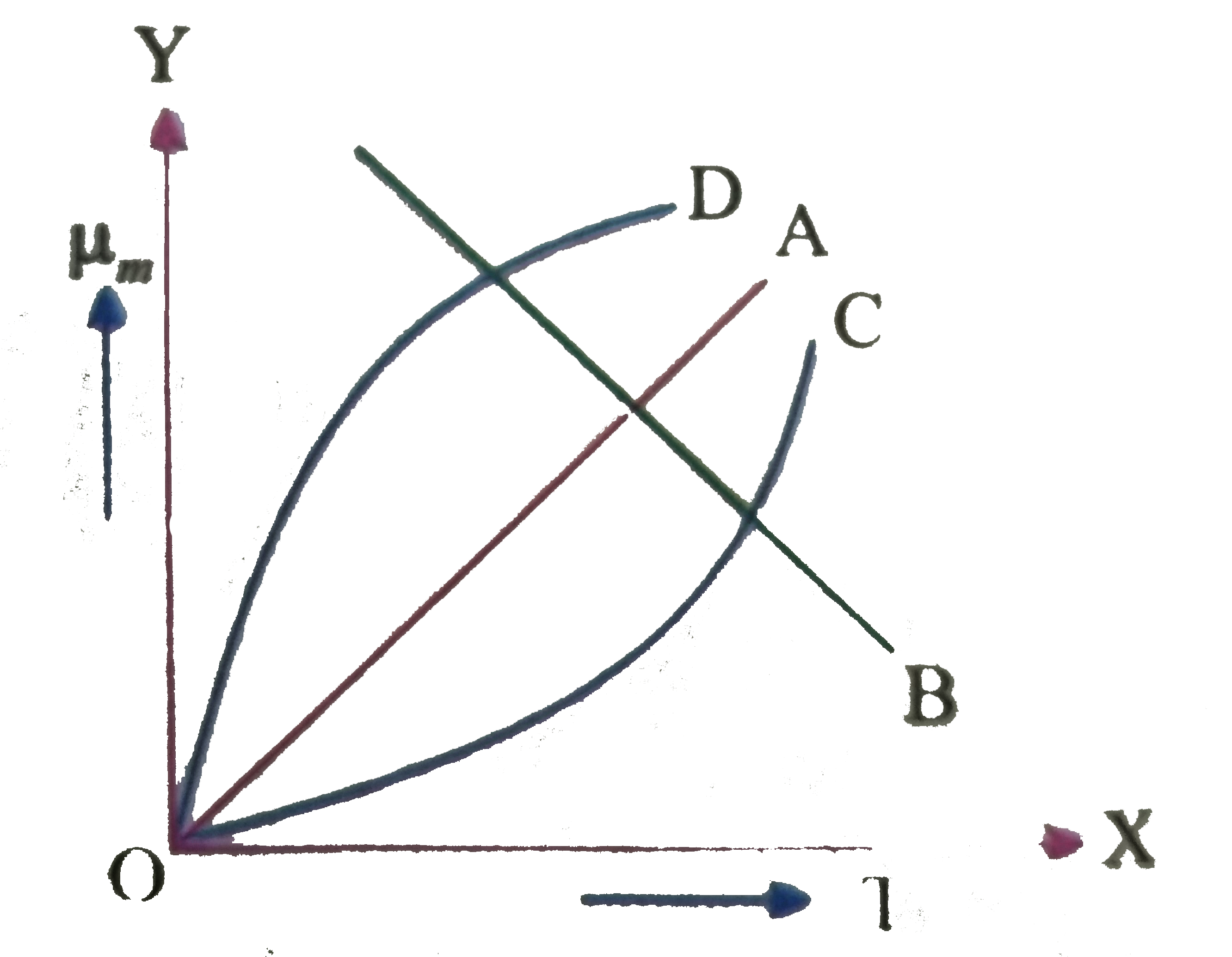
View SolutionThe frequency `(v_(m))` corresponding to which energy emitted by a black body is maximum may vary with temperature T of the body as shown in Which of the curves repersents correct variation ?
 .
.
View SolutionIf a black body is radiating at `T =1650K` at what wavelenght is the intensity maximum ? .
View SolutionTwo spherical bodies A (radius 6cm) and B (radius 18cm) are at temperature `T_(1)` and `T_(2)` respectively The maximum intensity in the emission spectrum of A is at `500 nm` and in that of `B` is at `1500nm` considering them to be black bodies, what will be the ratio of the rate of total energy radiated by A to that of `B` . ?
View SolutionFind the temperature of an oven if it radiates `8.28` cal per second through an opening whose area is `6.1cm cm^(2)` Assume that the radiation is close to that of a black body ? .
View SolutionThree very large plates of same area are kept parallel and close to each other. They are considered as ideal black surface and have very high thermal conductivity The first and thired plates are maintained at temperatures `2T` and `3T` respectively Find the temperature of the middle (i.e second) plate under steady state .
View SolutionA sphere with diameter of `80cm` is held at a temperature of `250^(@)C` and is radiating en-ergy If the intensity of the radiation detected at a distance of `2.0m` from the sphere 's cnetre is `102 W//m^(2)` What is the emissivity of the shere ? .
View SolutionOne end of a rod of length `20cm` is inserted in a furnace at `800K` The sides of the rod are coverd with an insulating meterial and the other end emits radiation like a black boy The temperature of this end is `750K` in the steady state The temperature of the surrounding air is `300K` Assuming radiation to be the only imporatant mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod Stefan's constant `sigma = 6.0 xx 10^(8) W m^(-2) K^(-4)` .
View SolutionA body cools from `80^(@)C` to `50^(@)C` in 5 minutes Calculate the time it takes to cool from `60^(@)C` to `30^(@)C` The temperature of the surroundings is `20^(@)C` .
View SolutionTwo sheres made of same material have their radii in the ratio `1:3` They are heated to the same temperature and kept in the same surroudings at a moderate temperature Show that the ratio of their initial rates of fall of temperature is `3:1` if the bodies are cooled by natural convection and radiation .
View Solution
Solved Example questions and complete solutions for chapter TRANSMISSION OF HEAT of NARAYANA PHYSICS (HINGLISH) of Class 11