Complete Solutions to EXERCISE IV of chapter WORK , ENERGY & POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK , ENERGY & POWER |
| NARAYANA | EXERCISE IV |
| Number Of Questions | 43 |
| Academic Year | 2023-24 |
A large slab of mass `5kg` lies on a smooth horizontal surface, with a block of mass `4kg` lying on the top of it. The coefficient of friction between the block and the slab is `0.25`. If the block is pulled horizontally by a force of F `=6N`, the work done by the force of friction on the slab, between the instants `t=2s` and `t=3s`, is `(g=10ms^-2)`

View SolutionIn the pulley - block system shown in figure, strings are light. Pulleys are massless and smooth. System is released from rest. In `0.3` seconds
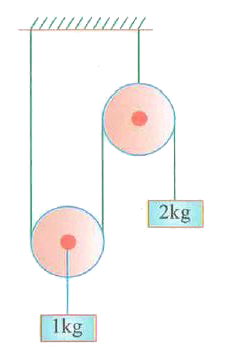
a) work done on 2 kg blocks by gravity is `6 J`
b) work done on 2 kg block by string is `-2J`
c) work done on 1 kg block by gravity is `-1.5 J`
d) work done on 1 kg block by string is 2 J
View SolutionA chain AB of length `l` is located in a smooth horizontal tube so that its fraction of length `h` hangs freely and touches the surface of the table with its end B(figure). At a certain moment the end A of the chain is set free. With what velocity will this end of the chain slip out of the tube?

View SolutionA ball of mass `m` is released from A inside a smooth wedge of mass `m` as shown in figure. What is the speed of the wedge when the ball reaches point B?
View SolutionA bob of mas `M` is suspended by a massless string of length `L`. The horizontal velocity `v` at position `A` is just sufficient to make it reach the point `B`. The angle `theta` at which the speed of the bob is half of that at `A`, satisfies.
 .
.
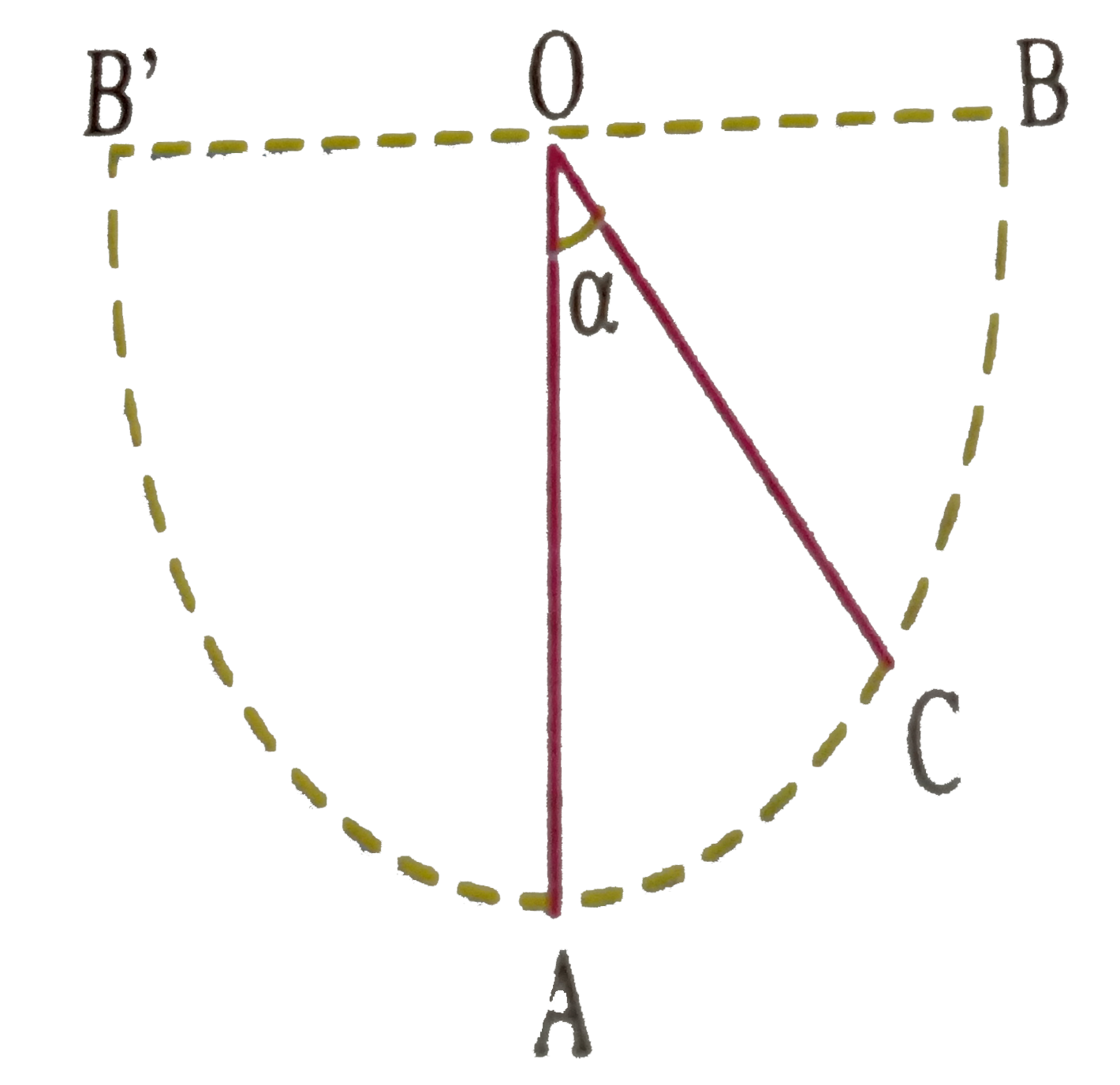
View SolutionA simple pendulum is vibrating with an angular amplitude of `90^(@)` as shown in the figure. For what value of a is the acceleration directed

i) vertically upwards
ii) horizontally
iii) vertically downward
View SolutionA projectile is fixed on a horizontal ground. Coefficient of restitution between the projectile and the ground is 'e'. If `a,b` and `c` be the ration of time of flight `[(T_(1))/(T_(2))]`, maximum height `[(H_(1))/(H_(2))]` and horizontal range `[(R_(1))/(R_(2))]` in first two collisions with the ground, then
View SolutionA ball `A` of mass `3 m` is placed at a distance `d` from the wall on a smooth horizontal surface Another ball `B` of mass `m` moving with velocity `u` collides with ball `A`. The coefficient of restitution between the balls and the wall and between the balls is `e`
(a) the velocity of ball `B` after collision is `(u(3e-1))/(4)`.
(b) the velocity of ball `B` after collision is `(u(2e-1))/(4)`.
( c) after collision, ball `A` will have away by distance `(d(2e-1))/((2e-1))` during the time ball `B` returns back to wall.
(d) after collision, ball `A` will move away by distance `(d(e-1))/((3e-1))` during the time ball `B` returns back to wall.
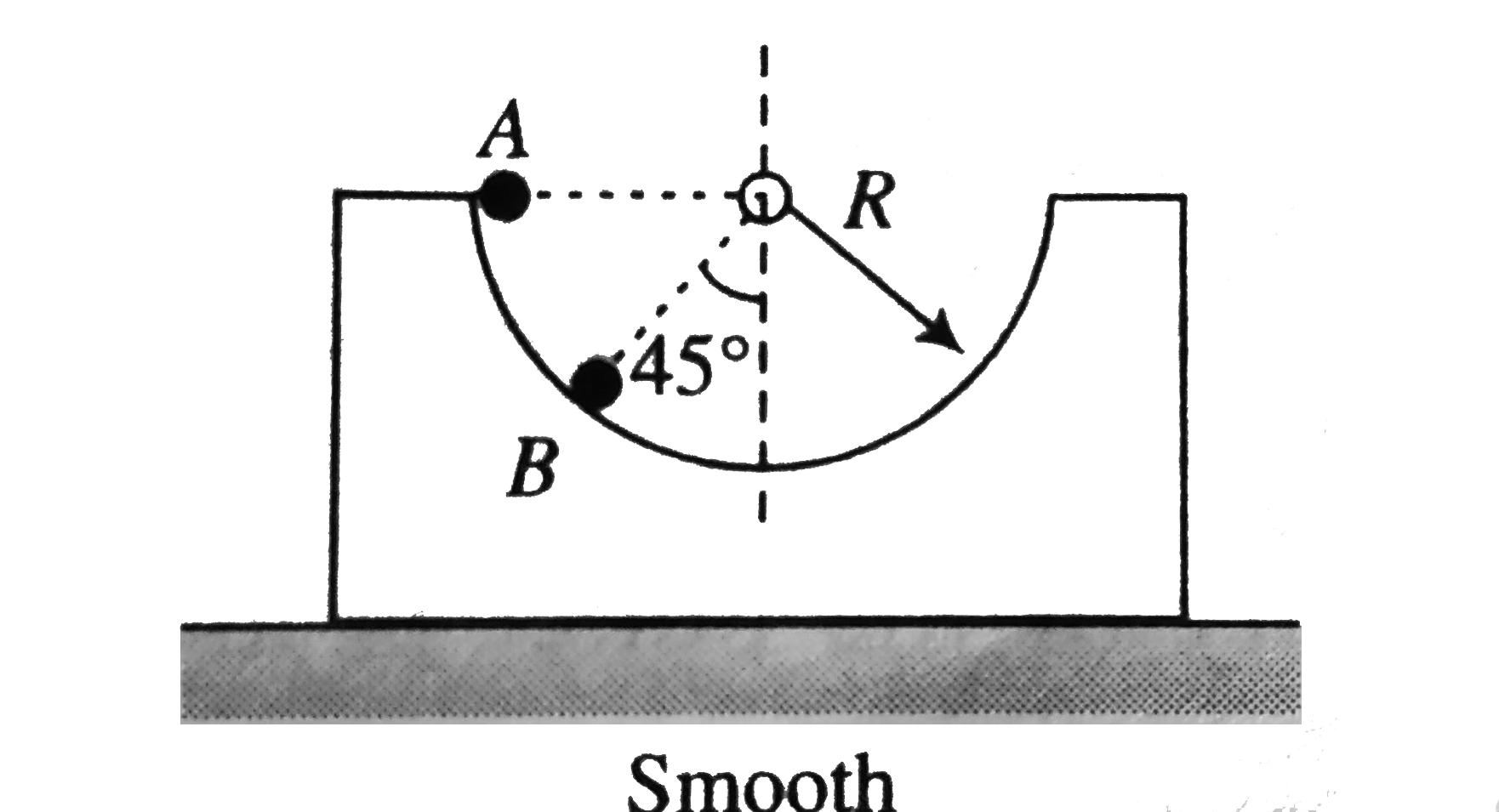
View SolutionFigure given below shows the variation of potential energy function U(x), corresponding to a particle lying in a one dimensional force field. The force acting on the particle at x = 2 m is:
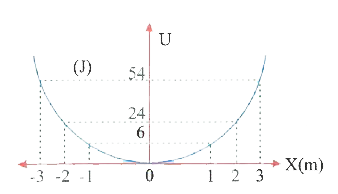
View SolutionA particles moves along a circle of a fixed radius with a variable acceleration given by `a_(n) = kt^(n),` where k is a constant and t time. If the power 'P' delivered by all forces acting on it be plotted against time 't' on a log-log scale, the slope of the straight line obtained is 2 as shown in Figure below. The value of n is:
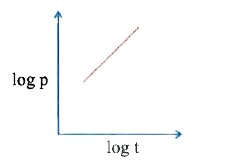
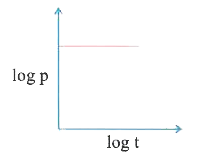
View SolutionA particle is moving along a circle of fixed radius such thta the power 'P' delivered by all the forces acting on it varies with time t as shown in figure. The angular acceleration `alpha `of the particle varies as:
View SolutionTwo blocks having masses 8 kg and 16 kg are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible string also connects B with ceiling as shown in figure at the initial moment. Initially the spring has its natural length.A constant horizontal force F is applied to the heavier block as shown. What is the maximum possible value of F so that lighter block doesn't loose contact with ground.
` (##NAR_NEET_PHY_XI_P2_C06_E11_012_Q01.png" width="80%">
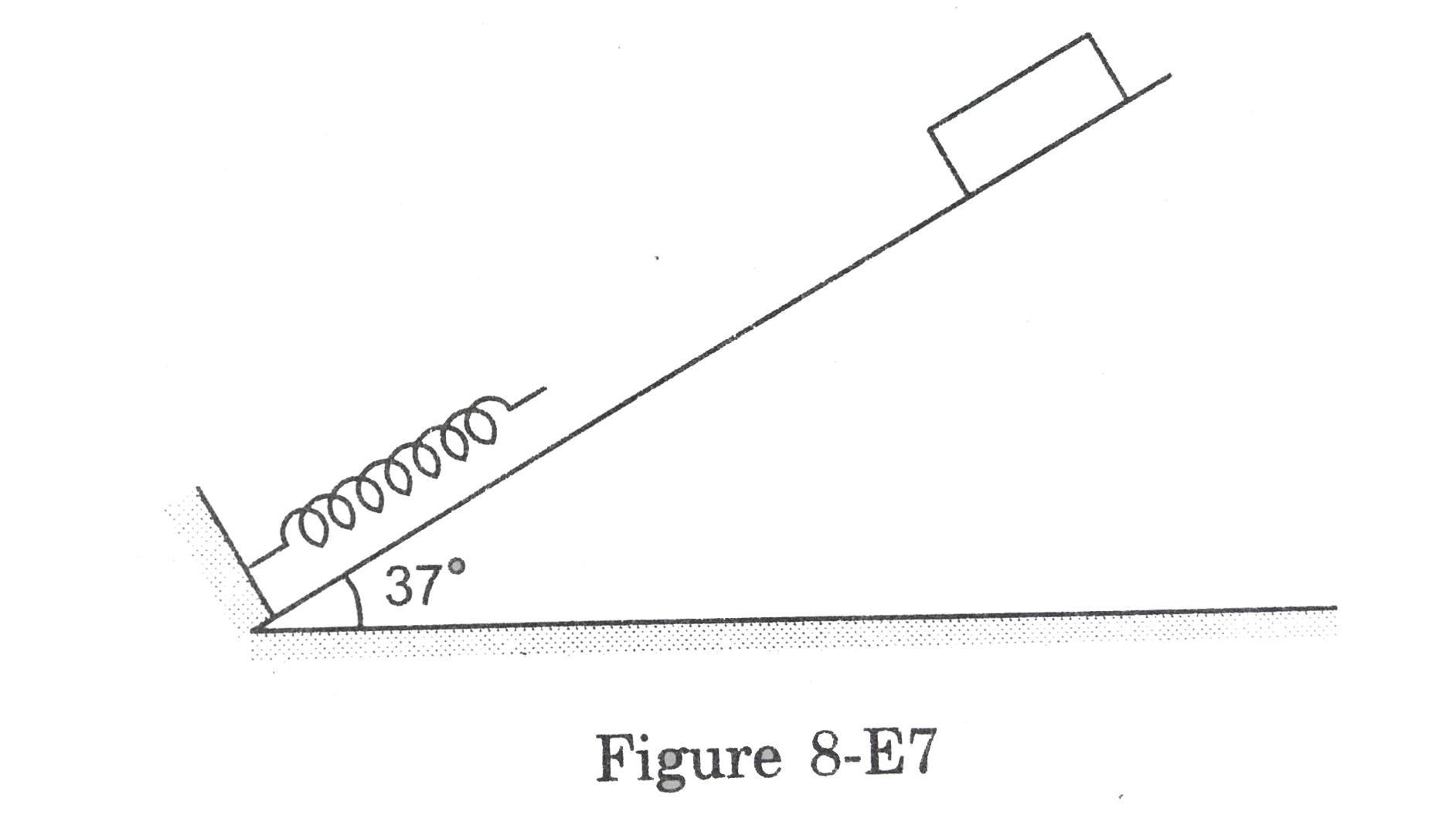
View SolutionFigure shows a spring fixed at the bottom end of an incline of inclination `37^0`. A small block of mass 2 kg starts slipping down the incline from a point 4.8 m away from the spring. The block compresses the spring by 20 cm, stops momentarily and then rebounds through a distance of 1 m up the incline. Find a. the frictioin coefficient between the plane and the block and b. the spring constant of the spring. Take `g=10 m/s^2`.
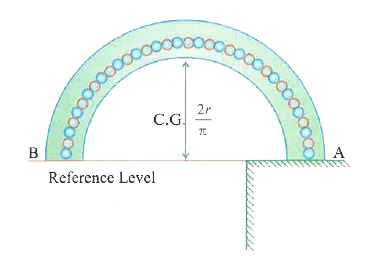
View SolutionA heavy flexible uniform chain of length `pi r` and mass `lambda pi r` lies in a smooth semicircular tube AB of radius 'r'. Assuming a slight disturbane to start the chain in motion, find the velocity v with which it will emerge from the end of the tube?
View SolutionA body slides without friction from a height `H = 60 cm` and then loops the loop of radius `R = 20 cm` at the bottom of an incline. Find the ratio of forces exerted on the body by the track at the positions `A,B` and `C (g = 10 ms^(-2))`.
 .
.
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length `l` is projected horizonally with speed `sqrt(gl)` . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View SolutionA cricket ball of mass 150 g moving with a speed of 123 km/h hits at the middle of the bat, held firmly at its position by the batsman.The ball moves straight back to the bowler after hitting the bat.Assuming that collision between ball and bat is completely elastic and the two remain in contact for `0.001s`, the force that the batsman had to apply to hold the bat firmly at its place would be
View Solution`n` elastic balls are placed at rest on a smooth horizontal plane which is circular at the ends with radius `r` as shown in the figure. The masses of the balls are `m`, `m/2`, `m/2^2`, …………….`(m)/(2^(n-1))` respectively. What is the minimum velocity which should be imparted to the first ball of mass `m` such that `n^th` ball completes the vertical circle

View SolutionThe `50 N` collar starts from rest at `A` and is lifted with a constant speed of `0.6 m//s` along the smooth rod. Determine the power developed by the force `F` at the instant shown.
 .
.
View SolutionA hose pipe has a diameter of `2.5 cm` and is required to direct a jet of water to a height of atleast `40 cm`. Find the minimum power of the pump needed for this hose.
View SolutionA body of mass m accelerates uniformly from rest to velocity `v_(0)` in time `t_(0)`. What is the instantaneous power delivered to the body when its velocity is `(v_(0))/(2)` ?
View SolutionA particle of mass `2 kg` starts moving in a straight line with an initial velocity of `2 m//s` at a constant acceleration of `2 m//s^(2)`. Then rate of change of kinetic energy.
View SolutionA lifting machine, having an efficiency of `80 %` uses `2500 J` of energy in lifting a `10 kg` load over a certain height. If the load is now allowed to fall through that height freely, its velocity at the end of the fall will be `(g =10 m//s^(2))`
View SolutionA 1kg block situated on a rough incline is connected to a spring of spring constant `100Nm^(-1)` as shown in figure,. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.
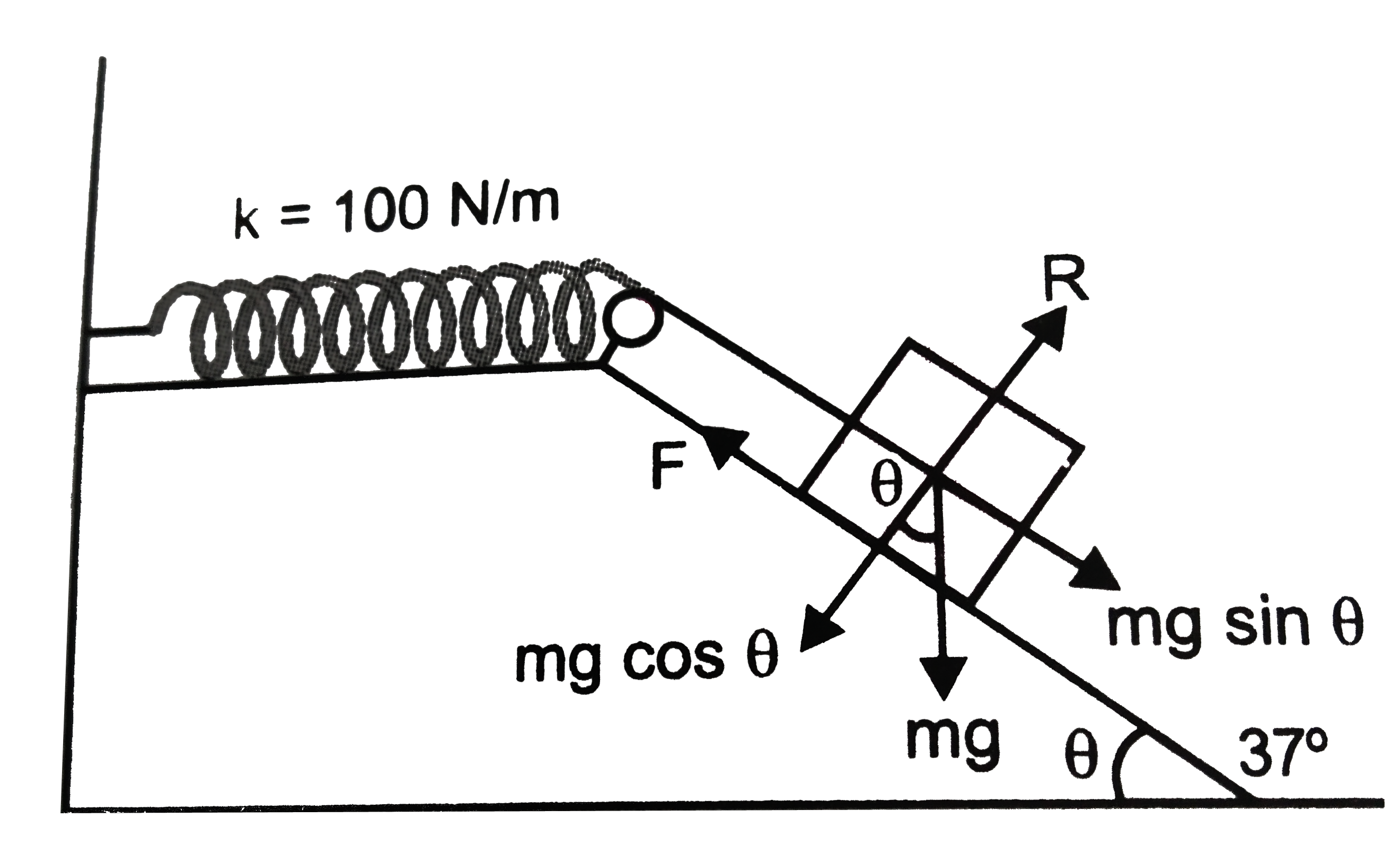
View SolutionA light spring of force constant 'K' is held between two blocks of masses 'm' and '2m'. The two blocks and the spring system rests on a smooth horizontal floor. Now th blocks are moved towards each other compressing the springs by 'x' and suddenly released. The relative velocity between the blocks when the spring attains its natural length will be
View SolutionDuring gas of negligible mass is sealed in a test tube of mass `50 gm` with the helo of a stopper of mass `3.5 gm`. The test tube is suspended from a fixed point with help of massless string such that the test tube is horizontal and distance between point of suspension and centre of mass of test tube is `25 cm`. The test tube is heated to a temperature due to which stopper is ejected out horizontally while test tube completes a vertical circle of radius `25 cm`. The minimum velocity with which stopper should be ejected out is
View SolutionA block is freely sliding down from a vertical height `4 m` on smooth inclined plane. The block reaches bottom of inclined plane and then it decribes vertical circle of radius `1 m` along smooth track. The ratio of normal reactions on the block while it crossing lowest point and highest point of vertical circle is
View SolutionThe length of a ballistic pendulum is `1 m` and mass of its block is `1.9 kg`. A bullet of mass `0.1 kg` strikes the block in horizontal direction with a velocity `100 ms^(-1)` and got embedded in the block. After collision the combined mass swings away from lowest point. The tension in the strings when it makes an angle `60^@` with vertical is `(g=10 ms^(-2))`.
View SolutionA stone attached to a string is rotated in a vertical circle such that when it is at the top of the circle its speed is `V` and there is neither tension nor slacking in the string. The speed of stone when its angular displacement is `120^@` from the lowest point is
View SolutionMass of the bob of a simple pendulum of length `L` is `m`. If the bob is projected horizontally from its mean position with velocity `sqrt(4 gL)`, then the tension in the string becomes zero after a vertical displacement of
View SolutionA wooden block of mass `10 gm` is dropped from the top of a cliff `100 m` high. Simultaneously a bullet of same mass is fired from the foot of the cliff vertically upwards with a velocity of `100 ms^(-1)`. If the bullet after collision gets embedded in the block, the common velocity of the bullet and the block immediately after collision is `(g=10 ms^(-2))`.
View SolutionA test tube of mass `20 gm` is filled with a gas and fitted with a stopper of `2 gm`. It is suspended horizontally by means of a thread of `1m` length and heated. When the stopper kicks out, the tube just completes a circle in vertical plane. The velocity with which the stopper kicked out is
View SolutionTwo bodies move towards each other and collide inelastically. The velocity of the first body is `2 m//s` and that of the seconf is `4m//sec` before impact. The common velocity after collision is `1 m//s` in the direction of the first body. The number of times did the `KE` of the first body exceed that of the second body before collision.
View SolutionA body A moves towards a wall with velocity `V`. The wall also moves towards the body `A` with velocity `V_(0)`. After collision the body moves in opposite direction with velocity `V^(1)` which is `(1+(2V_(0))/(V))` times the velocity `V`. The coefficient of restitution is
View SolutionA sphere `A` of mass `m` moving with a velocity hits another stationary sphere `B` of same mass. If the ratio of the velocity of the sphere after collision is `(v_(A))/(v_(B)) = (1 - e)/(1 + e)` where `e` is the coefficient of restitution, what is the initial
velocity of sphere `A` with which it strikes?
View SolutionAn electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because,
View SolutionA proton is kept at rest. A positively charged particle is released from rest at a distance `d` in its field. Consider two experiments, one ini which the charged particle is also a proton and in another, a position. In the same time `t`, the work done on the two moving charged particles is
View SolutionA man squatting on the ground gets straight up and stand. The force of reaction of ground on the man during the process is.
View SolutionA cyclist comes to a skidding stop in `10m`. During this process, the force on the cycle due to the road is `200N` and is directly opposite to the motion.
a. How much work does the road do on the cycle?
b. How much work does the cycle do on the road?
View SolutionA body is falling freely under the action of gravity alone in vacuum. Which of the following quantities remain constant during the fall ?
View SolutionDuring inelastic collision between two bodies, which of the following quantities always remain conserved ?
View SolutionA mass of `5kg` is moving along a circular path or radius `1m`. If the mass moves with 300 revolutions per minute, its kinetic energy would be
View SolutionIn a shotput event an athlete throws the shotput of mass `10 kg`with an initial speed of `1 ms^(-1)` at `45^@` from a height `1.5 m` above ground. Assuming air resistance to be negligible and acceleration due to gravity to be `10 ms^(-2)`, the kinetic energy of the shotput when it just reaches the ground will be
View Solution
EXERCISE IV questions and complete solutions for chapter WORK , ENERGY & POWER of NARAYANA PHYSICS (HINGLISH) of Class 11