Complete Solutions to ILLUSTRATION of chapter WORK , ENERGY & POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK , ENERGY & POWER |
| NARAYANA | ILLUSTRATION |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
If the magnitude of two vectors are 4 and 6 and the magnitude of their scalar product is `12sqrt2` what is the angle between the vectors?
View SolutionFind the angle between force `vec F = ( 5 hat i + 4 hat j + 5 hat k)` unit and displacement `vec d = (3 hat i + 4 hat j - 3 hat k)` unit. Also find the projection of `vec F on vec d.`
View SolutionA block of mass `5kg` is being raised vertically upwards by the help of a string attached to it. It rises with an acceleration of `2ms^-2`. Find the work done by the tension in the string if the block rises by `2.5m`. Also find the work done by the gravity and the net work done.
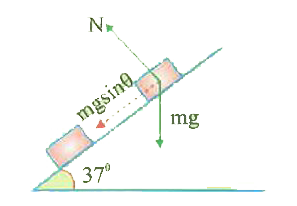
View SolutionA block of mass 4 kg slides down a plane inclined at `37^(@)` with the horizontal. The length of plane is 3 m. find work done by normal force , gravity and frictional force .
View SolutionA box is moved over a horizontal path by applying force `F = 60 N` at an angle `theta = 30^(@) w.r.t` the horizontal. What is the work done during the displacement of the box over a distance of `0.5 km`.
View SolutionA load of mas m = 300kg is lifted by a winch with an acceleration `a = 2 m/s^(2)`. Find the work done during the first one and a half seconds from the beginning of motion.
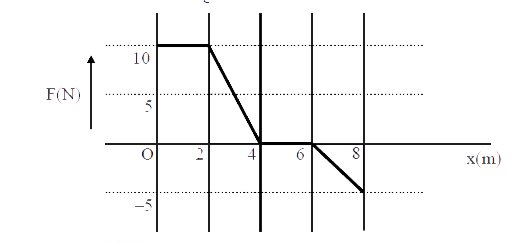
View SolutionA 5 kg block moves in a straight line on a horizontal frictionless surface under the influence of a force that varies with position as shown in the figure. Find the work done by this force as the block moves from the origin to x = 8m.
View SolutionA block of mass m = 4 kg is dragged 2 m along a horizontal surface by a force F = 30 N acting at `53^(@)` to the horizontal. The initial speed is `3 m//s and mu_(k) = 1//8`.
Find its final speed
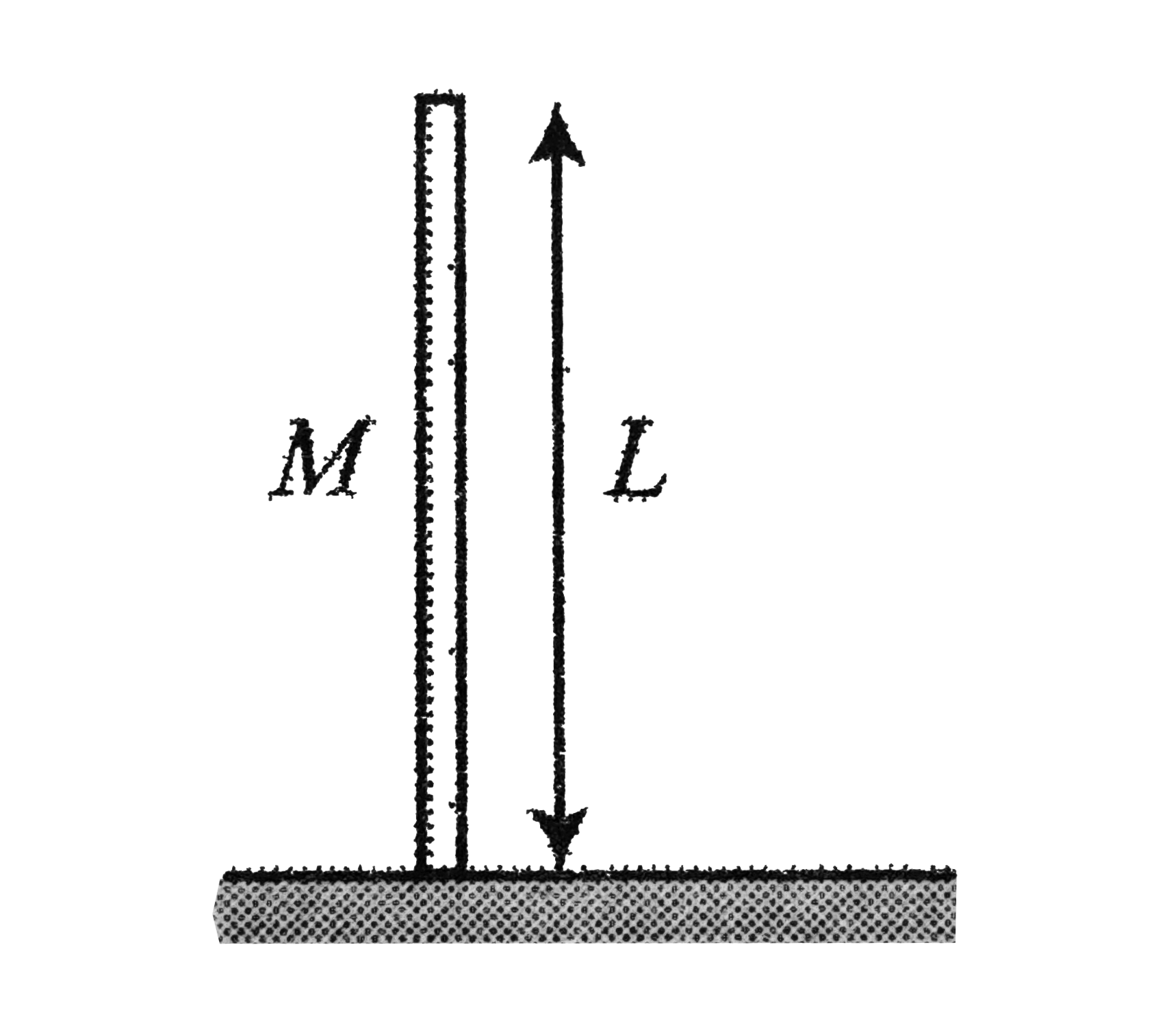
View SolutionA uniform rod of mass M and length L is held vertically upright on a horizontal surface as shown in figure. Assuming zero potential energy at the base of the rod, determine the potential energy of the rod.
View SolutionA particle is projected at ` 60(@)` to the horizontal with a kinetic energy `K` . The kinetic energy at the highest point is
View SolutionAn athlete in the Olympic gamed covers a distance of `100 m` in `10 s`. His kinetic energy can be estimated to be in range.
(1) `200 J - 500 J`
(2) `2 xx 10^(5) J - 3 xx 10^(5) J`
(3) `20,000 J - 50,000 J`
(4) `2,000 J - 5,000 J`.
View SolutionKinetic energy of a particle moving along a circle of radisu R depends on the distance covered as `K =as^(2)` where a is a constant . Find the force acting on the particle as a function of s.
View SolutionA rectangular plank of mass `m_(1)` and height 'a' is on a horizontal surface. On the top of it another rectangular plank of mass `m_(2)` and height 'b' is placed. Find the potential energy of the system ?
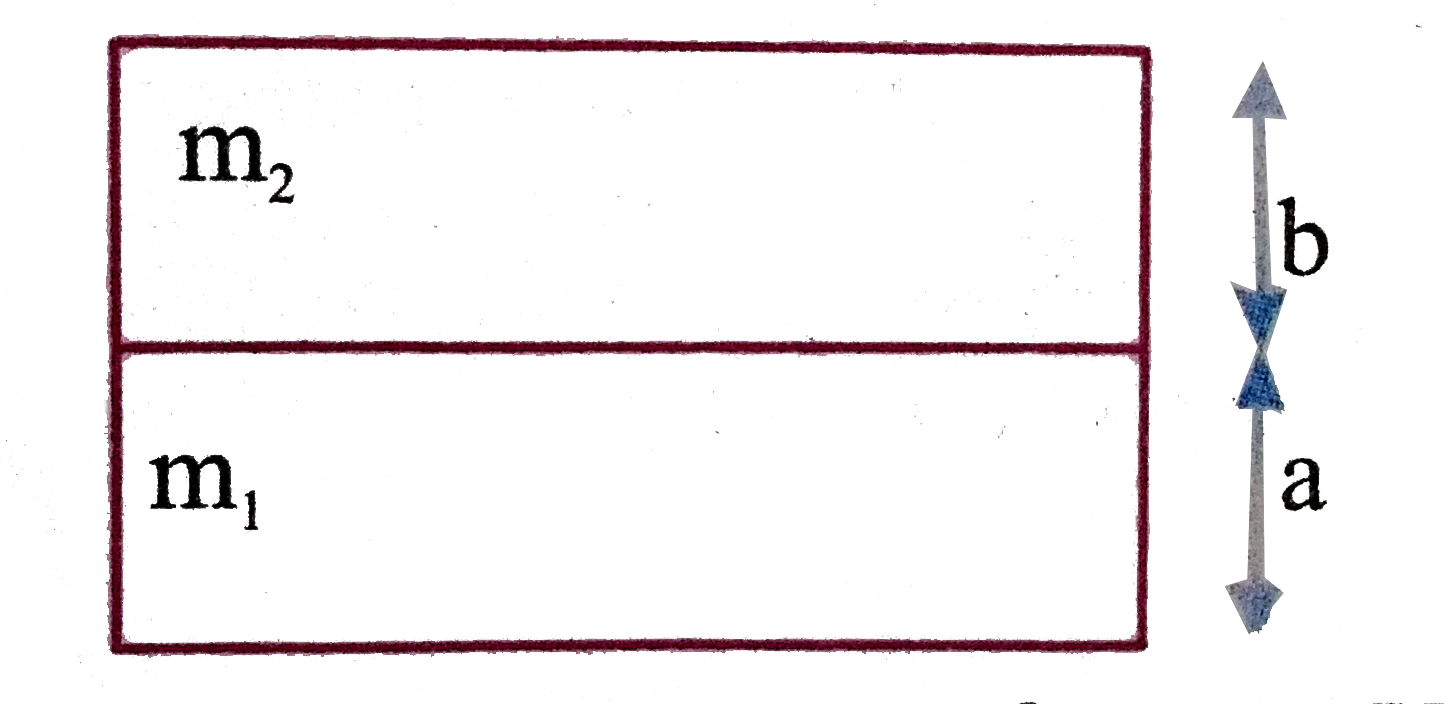 .
.
View SolutionA chain of length l and mass m lies of the surface of a smooth hemisphere of radius `Rgtl` with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.

View SolutionAn elastic spring of unstretched length L and force constant k is stretched by a small length x. It is further stretched by another small length y. Work done during the second stretching is
View SolutionThe position (x) of a particle of mass 1 kg moving along x-axis at time t is given by `(x=(1)/(2)t^(2))` metre. Find the work done by force acting on it in time interval from t=0 to t=3 s.
View SolutionUnder the action of a force, a `2 kg` body moves such that its position x as a function of time is given by `x =(t^(3))/(3)` where x is in metre and t in second. The work done by the force in the first two seconds is .
View SolutionA uniform chain of length 1 and mass m is kept on a smooth table. It is released from rest when the overhaning part was `n^(th)` fraction of total length. Find the kinetic energy of the chain as it completely slips off the table
View SolutionA 2 kg block slides on a horizontal floor with a speed of 4 m/s. It strikes an uncompressed spring, and compresses it till the block is motionless. The kinetic friction force is 15 N and spring constant is 10000 N/m. The spring is compressed by (in cm):
View SolutionIn the below figure, what constant force 'P' is requried to bring the `50 kg` body, which starts from rest to a velocity of `10 m//s` in moving `7 m` along the plane ? (Neglect friction).
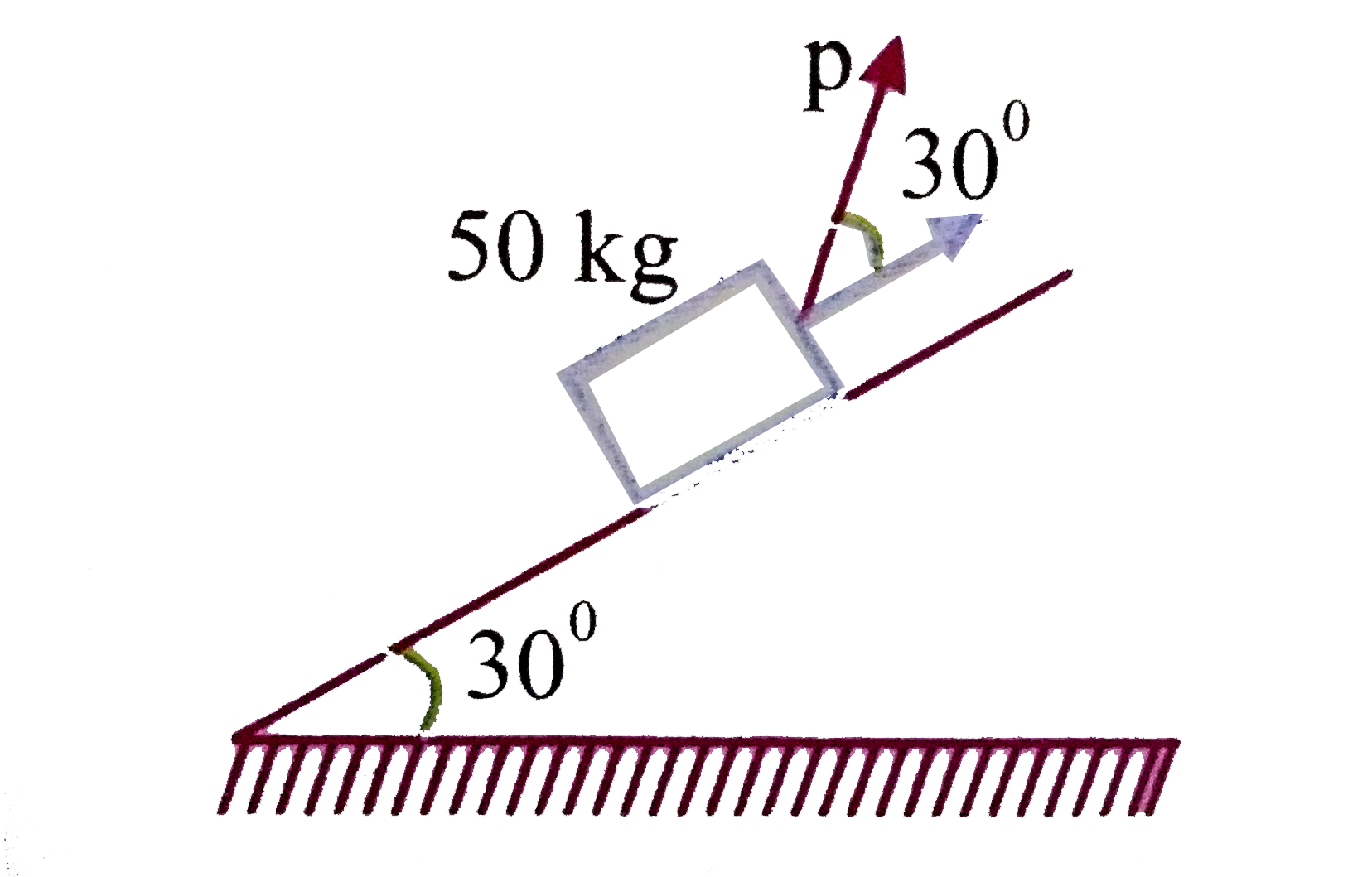 .
.
View SolutionIn a molecule, the potential energy between two atoms is given by `U (x) = (1)/(x^(12)) -(b)/(x^(6))`. Where 'a' and 'b' are positive constants and 'x' is the distance between atoms. Find the value of 'x' at which force is zero and minimim `P.E` at that point.
View SolutionThe potential energy for a conservative force system is given by `U=ax^(2)-bx`. Where a and b are constants find out (a) The expression of force (b) Potential energy at equilibrium.
View SolutionThe potential energy of a particle of mass 1 kg free to move along x-axis is given by `U(x) =(x^(2)/2-x)` joule. If total mechanical energy of the particle is 2J then find the maximum speed of the particle. (Assuming only conservative force acts on particle)
View SolutionA massless platform is kept on a light elastic spring as shown in figure. When a small stone of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the spring compresses by 0.01m. From what height should the stone be droppped to cause a compression of 0.04m in the spring ?
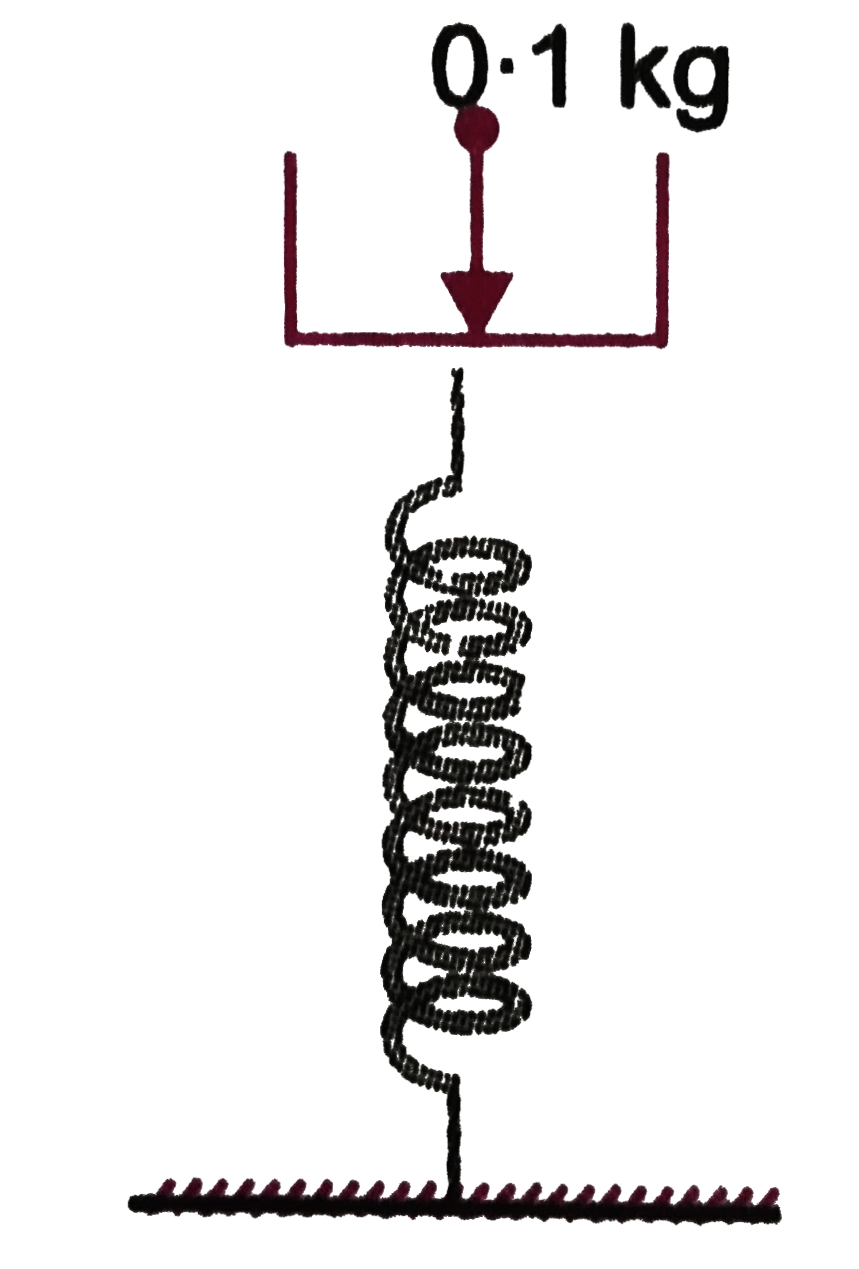
View SolutionA small mass 'm' is sliding down on a smooth curved incline form a height 'h' and finally moves through a horizontal smooth surface. A light spring of force constant `K` is fixed with a vertical rigid stand on the horizontal surface, as shown in the figure. Find the value for the maximum compression in the spring if mass 'm' is released from rest from height 'h' and hits the spring in the horizontal surface.
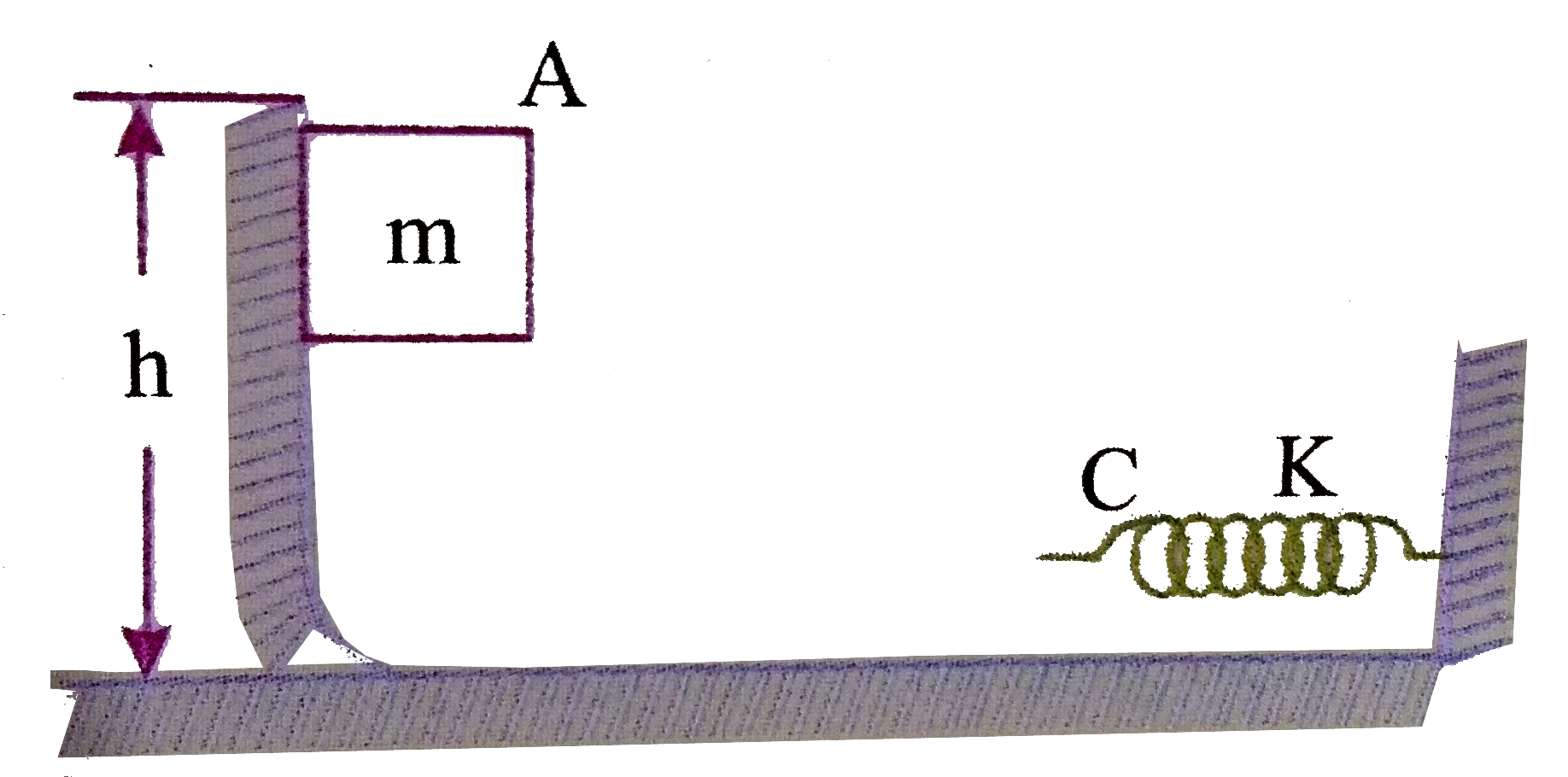 .
.
View SolutionA vehicle of mass `15` quintal climbs up a hill `200 m` high. It then moves on a level road with a speed of `30 ms^(-1)`. Calculate the potential energy gained by it and its total mechanical energy while running on the top of the hill.
View SolutionA particle is released from height `H`. At cartain height from the ground its kinetic energy is twice its gravitational potential energy. Find the height and speed of particle at that height.
View SolutionThe potential energy of a 1kg particle free to move along the x-axis is given by `V(x)=(x^(4)/4-x^(2)/2)J` The total mechanical energy of the particle is 2J then the maximum speed `(in m//s)` is
View Solution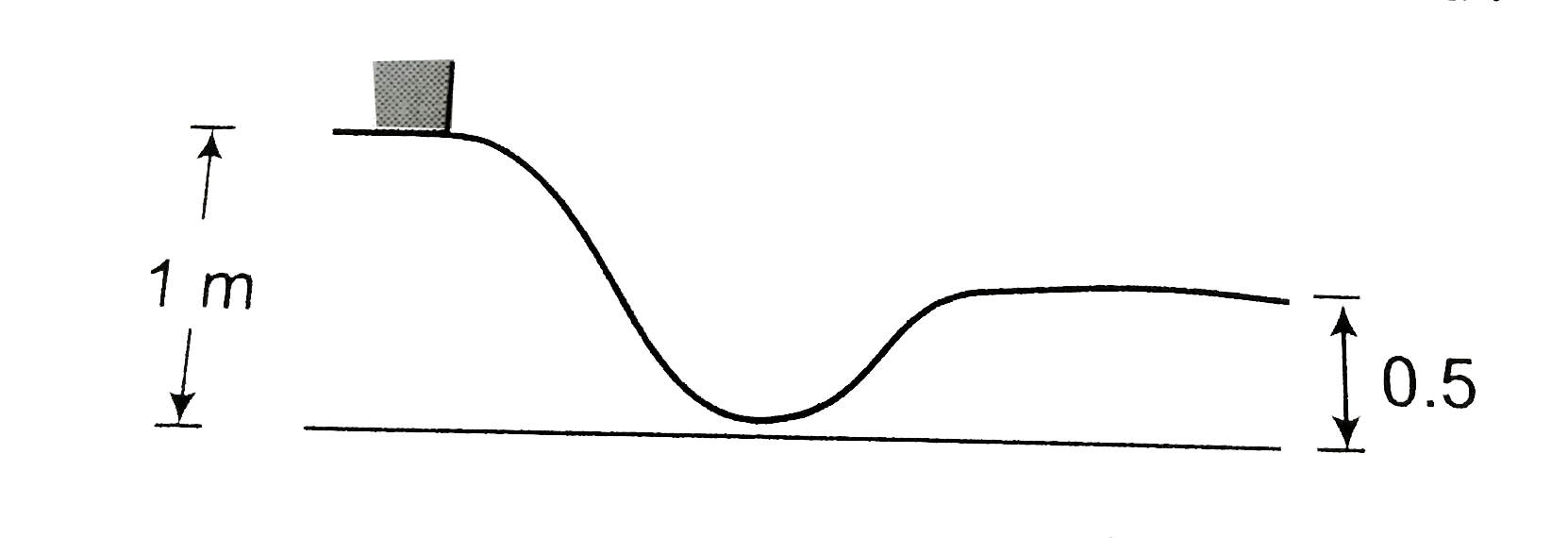
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point `A`, how far away from the track will the particle hit the ground?
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetricaly tostretch the spring by a length x over its natural length. The work doen by the spring oneach mass is
View SolutionA block is placed on the top of a plane inclined at `37^@` with horizontal. The length of the plane is `5m`. The block slides down the plane and reaches the bottom.
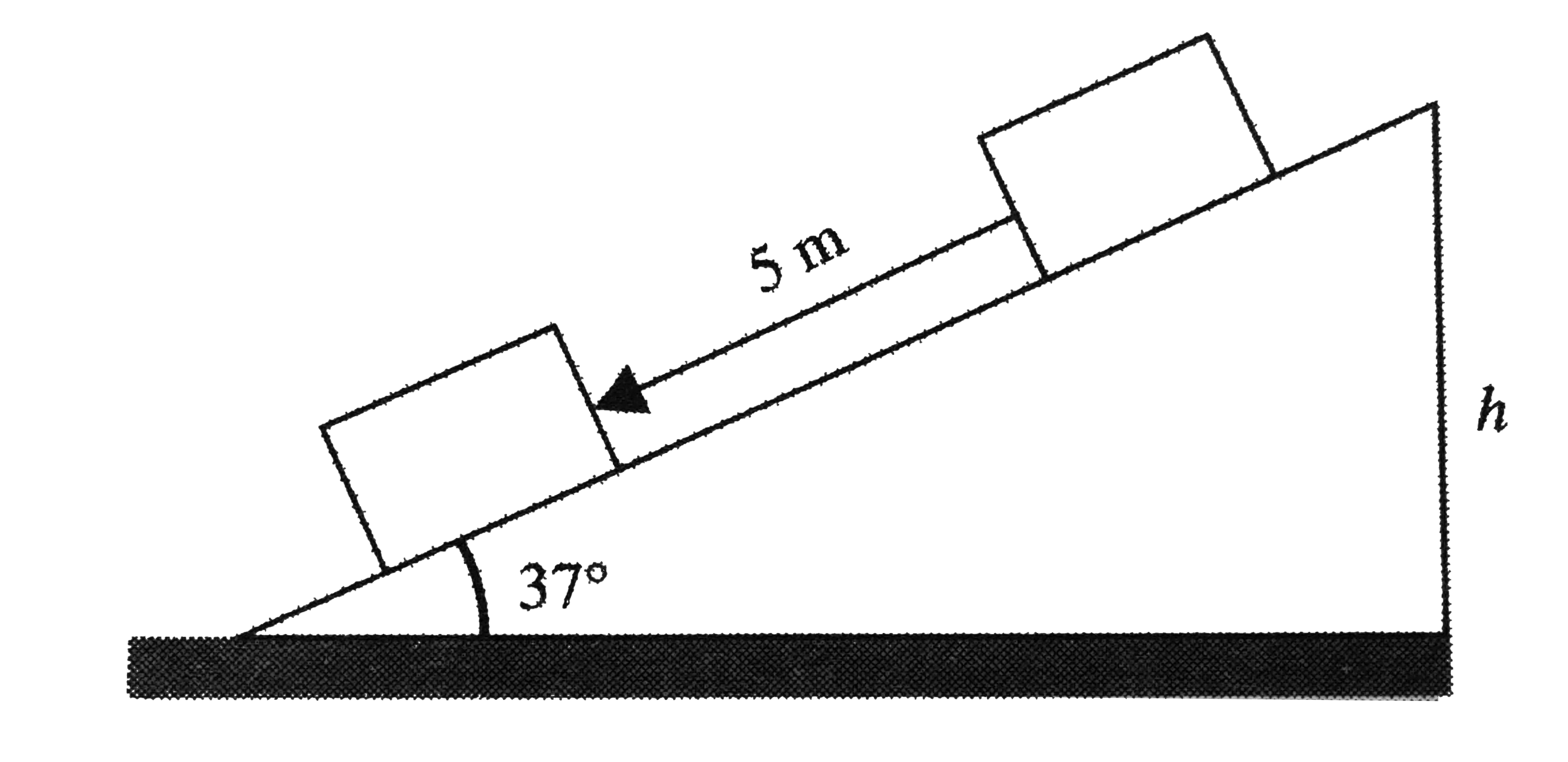
a. Find the speed of the block at the bottom if the inclined plane is smooth.
b. Find the speed of the block at the bottom if the coefficient of friction is `0.25`.
View Solution1 kg block collides with a horizontal massless spring of force constant `2 N//m`. The block compresses the spring by 4m. If the coefficient of kinetic friction between the block and the· surface is 0.25, what was the speed of the block at the instant of collision? (take `g = 10 m//s^(2)`)

View SolutionA uniform chain of length l and mass m lies on a smooth table. A very small part of this chain hangs from the table. It begins to fall under the weight of hanging part. Find the velocity of chain when the length of hanging part becomes y.
View SolutionA mass m is tied to a string of length l and is rotated in a vertical circle with centre at the other end of the string.
(a) Find the minimum velocity of the mass at the top of the circle so that it is able to complete the circle.
(b) Find the minimum velocity at the bottom of the circle corresponding to the above condition.
View SolutionA body slides down an inclined surface which ends into a vertical loop of radius R = 40cm.
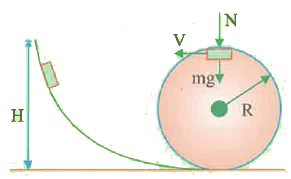
What must be the height H of the inclined surface for the body so that it does not leave contact with the surface even at the uppermost point of the loop? Assume friction to be absent.
View SolutionThe potential energy of a particle in a certain field has the form `U=(a//r^2)-(b//r)` , where a and b are positive constants and r is the distance from the centre of the field. Find the value of `r_0` corresponding to the equilibrium position of the particle, examine whether this position is stable.
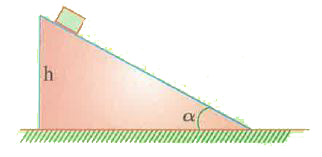
View SolutionA mass m slides down a fixed plane inclined at an angle a to the horizontal plane after covering the entire length of the inclined plane. The height of the inclined plane is h and the coefficient of friction over both surfaces is `mu`.
View SolutionIn the given system, when the ball of mass m is released, it will swing down the dotted circular are. A nail is located at a distance d below the point of suspension as shown in figure.
(a) How fast will it reach the lowest point in its swing?
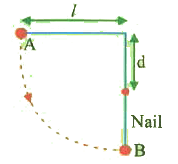
(b) Show that d must be at least `0.6 l,` if the ball is to swing completely around a circle centered along the nail.
(c) If `d = 0.6 l, find the change in tension in the string just after it touches the nail.
View SolutionA small sphere tied to the string of length `0.8m` is describing a vertical circle so that the maximum and minimum tensions in the string are in the ratio `3:1`. The fixed end of the string is at a height of `5.8m` above ground.
(a) Find the velocity of the sphere at the lowest position.
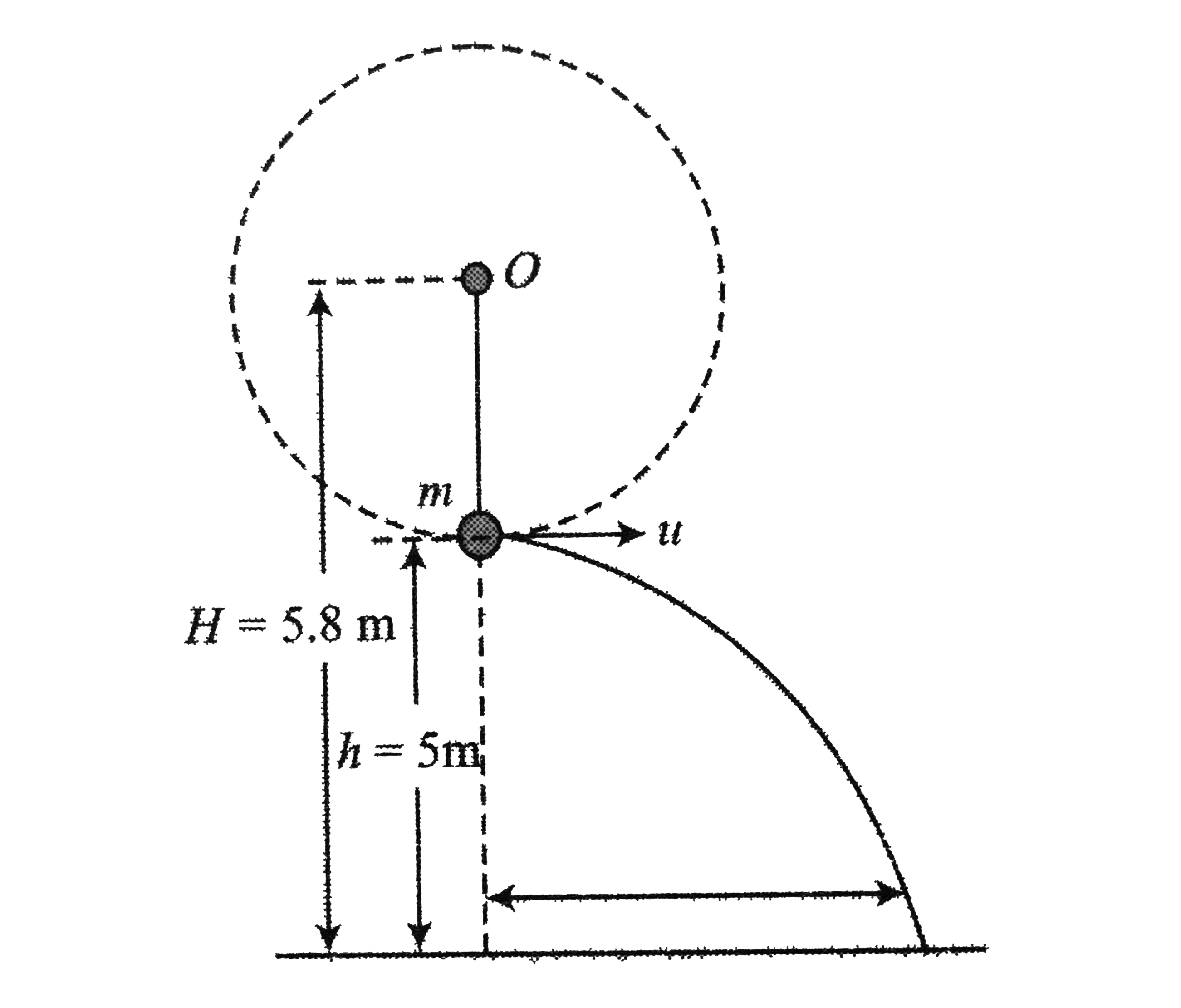
(b) If the string suddenly breaks at the lowest position, when and where will the sphere hit the ground?
View SolutionA pump is required to lift `1000kg` of water per minute from a well `20m` deep and eject it at a rate of `20ms^-1`.
a. How much work is done in lifting water?
b. How much work is done in giving in KE?
c. What HP(horsepower) engine is required for the purpose of lifting water?
View SolutionAn automobile is moving at `100 kmph` and is exerting attractive force of `3920 N`. What horse power must the engine develop, if `20 %` of the power developed is wasted ?
View SolutionThe `50 N` collar starts from rest at `A` and is lifted with a constant speed of `0.6 m//s` along the smooth rod. Determine the power developed by the force `F` at the instant shown.
 .
.
View SolutionA machine delivers power to a body which is directly proportional to velocity of the body. If the body starts with a velocity which is almost negligible, find the distance covered by the body in attaining a velocity `v`.
View SolutionFind the power of an engine which can draw a train of `400` metric ton up the inclined plane of `1` in `98` at the rate `10 ms^(-1)`. The resistance due to friction acting on the train is `10 N` per ton.
View SolutionA hose pipe has a diameter of `2.5 cm` and is required to direct a jet of water to a height of atleast `40 cm`. Find the minimum power of the pump needed for this hose.
View SolutionA body of mass `m` accelerates uniformly from rest to velocity `v_(0)` in time `t_(0)`, find the instantaneous power delivered to body when velocity is `(v_(0))/(2)`.
View SolutionTwo billiard balls of same size and mass are in contact on a billiard table. A third ball of same mass and size strikes them symmetrically and remains at rest after the impact. Find the coefficient of restitution between the balls?
View SolutionA ball drops from a ceiling of a room and after rebounding twice from the floor reaches a height equal to half that of the ceiling. Show that the coefficient of restitution is `sqrt(1/2)`
View SolutionA bullet of mass `2 g` travelling at a speed of `500 m//s` is fired into a ballistic pendulum of mass `1.0 kg` suspended from a cord `1.0 m` long. The bullet penetrates the pendulum and emerges with a velocity of `100 m//s`. Through what vertical height will the pendulum rise?
View SolutionEach of the blocks shown in figure has mass 1 kg. The rear block moves with a speed of 2 m/s towards the front block kept at rest. The spring attached to the front block is light and has a spring constant 50 N/m. find the maximum compression of the spring.

View Solution
ILLUSTRATION questions and complete solutions for chapter WORK , ENERGY & POWER of NARAYANA PHYSICS (HINGLISH) of Class 11