Complete Solutions to EXERCISE -II (H.W) of chapter WORK , ENERGY & POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK , ENERGY & POWER |
| NARAYANA | EXERCISE -II (H.W) |
| Number Of Questions | 75 |
| Academic Year | 2023-24 |
Velocity-time graph of a particle of mass (2 kg) moving in a straight line is as shown in Fig. 9.20. Find the word done by all the forces acting on the particle.
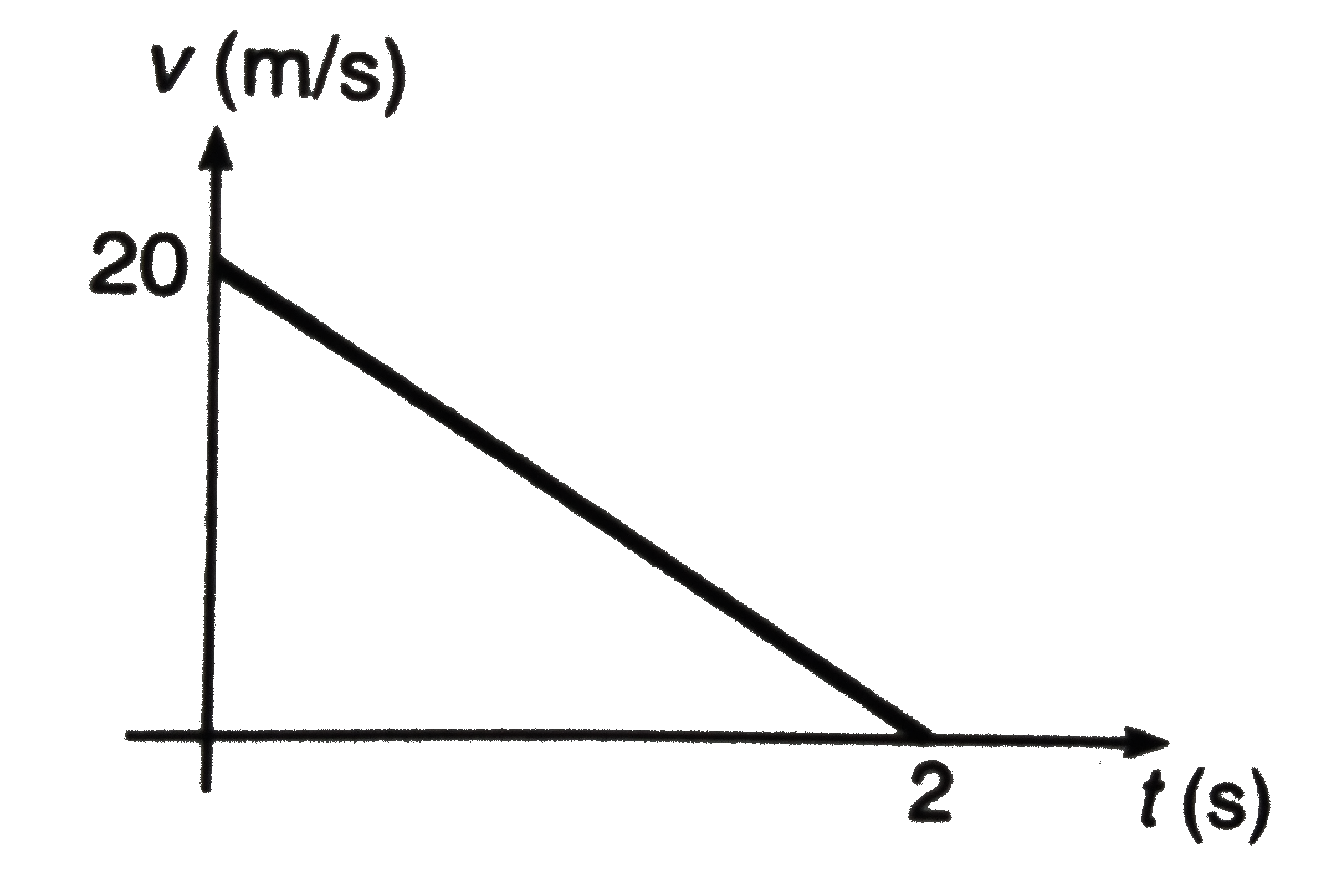 .
.
View SolutionThe displacement of a body of mass `2 kg` varies with time `t` as `S = t^(2) + 2t`, where `S` is in seconds. The work done by all the forces acting on the body during the time interval `t = 2s` to `t = 4s` is
View SolutionTh ework done in moving a body of mass `4 kg` with uniform velocity of `5 ms^(-1)` for `10` second on a surface of `mu = 0.4 is (take g= 9.8m//s^(2))`
View SolutionA body is acted upon by a force which is inversely proportional to the distance covered. The work done will be proportional to
View SolutionA particle of mass `0.5 kg` is displaced from position `vec r_(1)(2,3,1)` to`vec r_(2)(4,3,2)` by applying a force of magnitude `30 N` which is acting along `(hati + hatj + hatk)`. The work done by the force is
View SolutionKinetic energy of a particle moving in a straight line varies with time `t` as `K = 4t^(2)`. The force acting on the particle
View SolutionA force `F` acting on a particle varies with the position `x` as shown in the graph. Find the work done by the force in displacing the particle from `x =-a` to `x = +2a`.
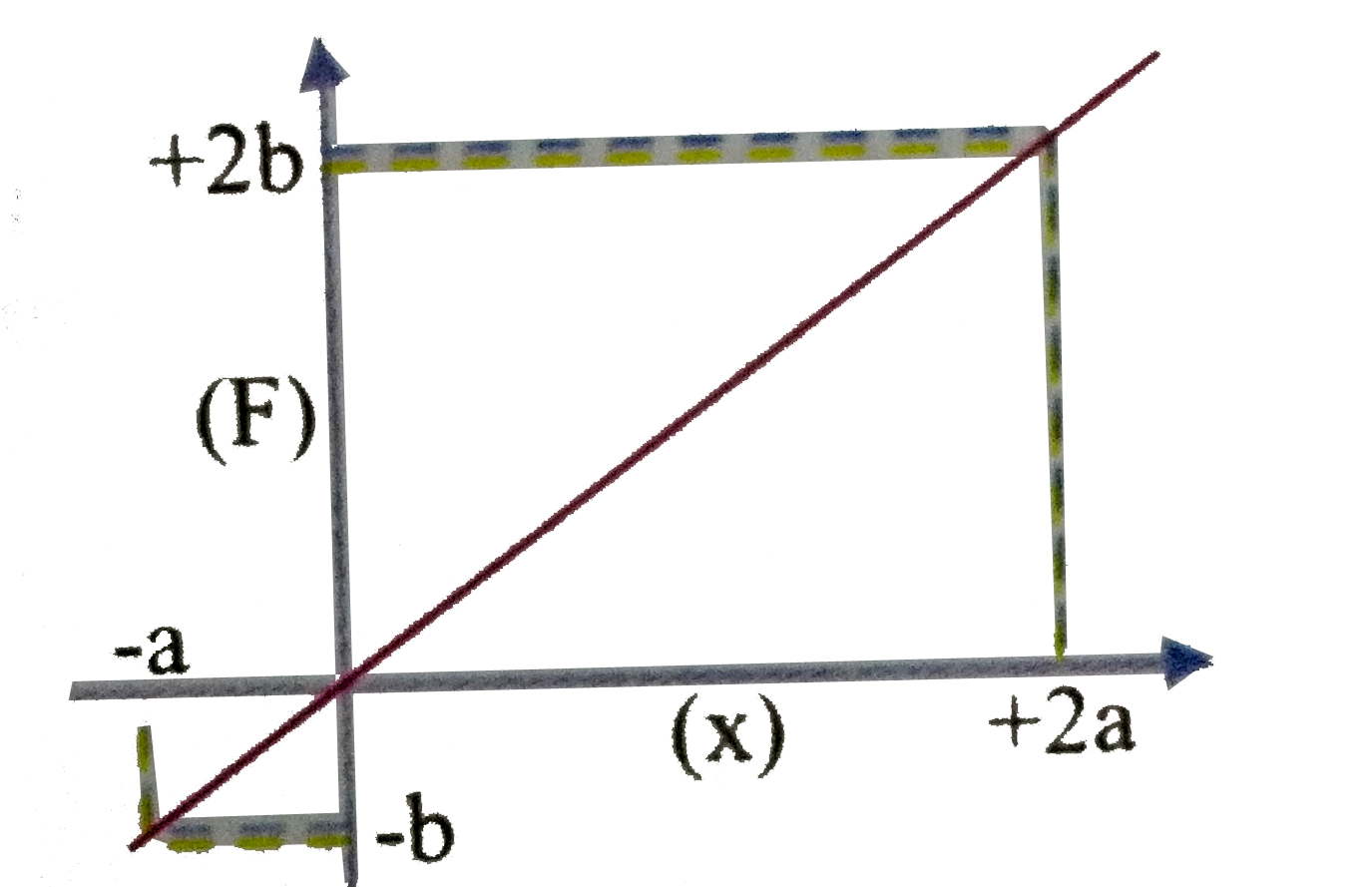 .
.
View SolutionA force `vec F=(2 hat i + 3hat j \- 4 hat k)N` acts on a particle moves `5 sqrt(2)m`, the work done by force in joule is
View SolutionTwo forces each of magnitude `10 N` act simultaneously on a body with their directions inclined to each other at an angle of `120^@`and displaces the body over `10 m` along the bisector of the angle between the two forces. Then the work done by force is
View SolutionA body is displaced from `(0,0)` to `(1 m, 1m)` along the path `x = y` by a force `F=(x^(2) hatj + y hati)N`. The work done by this force will be
View SolutionA body of mass `5 kg` at rest under the action of a force which gives its velocity given by `v = 3 xx t m//s`, here 't' is time in seconds. The work done by the force in two seconds will be
View SolutionA particle is made to move from the origin in three spells of equal distances, first along the x -axis, second parallel to y-axis and third parallel to z -axis. One of the forces acting on it is has constant magnitude of 50 N and always acts along the direction of motion Work done by this force in the three spells of motion are equal and total work done in all the three spells is 300 J. The final coordinates of the particle will be :-
View SolutionA position dependent force F ia acting on a particle and its force-position curve is shown in the figure. Work done on the particle, when its displacement is from 0 to 5 m is
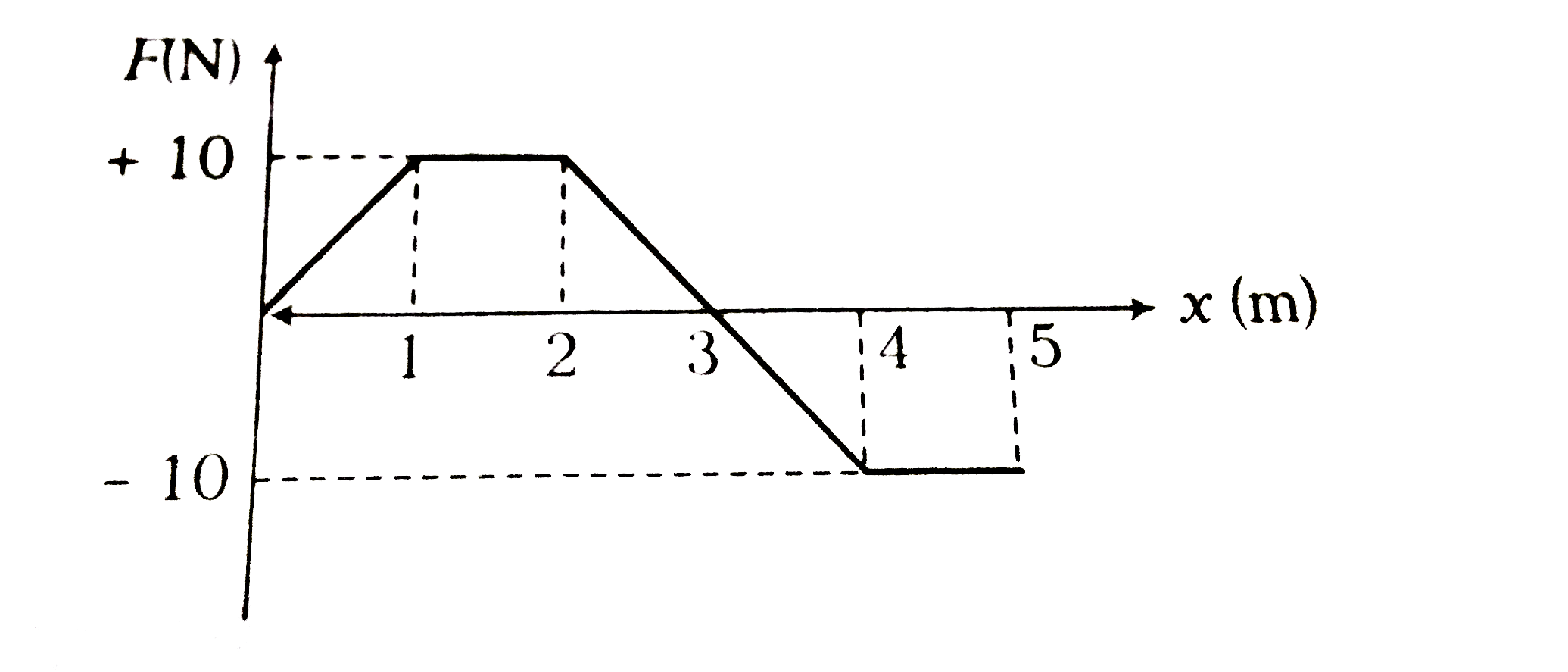
View SolutionA force F acting on an object varies which distance x as shown in the figure. The force is in N and x in m. The work done by the force in moving the object from x = 0 to x = 6 m is

View SolutionA body of mass m is allowed to fall with the help of string with downward acceleration g/6 to distance x. The work done by the string is
View SolutionAcceleration versus time graph of a particle moving in a straight line is as shown in adjoining figure. If initially particle was at rest. Then corresponding kinetic energy versus time graph will be :

View SolutionA rubber ball falling from a height of `5 m` rebounds from hard floor to a height of `3.5 m`. The `%` loss of energy during the impact is
View SolutionAn elastic spring is compressed between two blocks of masses `1 kg` and `2 kg` resting on a smooth horizontal table as shown. If the spring has `12 J` of energy and suddenly released, the velocity with which the larger block of `2 kg` moves will be
 .
.
View SolutionA block of mass `2 kg` is on a smooth horizontal surface. A light of force constant `800 N//m` has one end rigidly attached to a vertical wall and lying on that horizontal surface. Now the block is moved towards the wall compressing the spring over a distance f `5 cm` and then suddenly released. By the time the spring regains its natural length and looses contact with the block, the velocity acquired by the block will be
View Solutionn' identical cubes each of mass 'm' and edge 'L' are on a floor. If the cubes are to be arranged one over the other in a vertical stack, the work to be done is
View SolutionA vertically projected body attains the maximum height in `6s`. The ratio of kinetic energy at the end of `3^(rd)` second to decrease in kinetic energy in the next three seconds is
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as `K=as^2`. The force acting on the particle is
View SolutionA uniform chain of mass `m` and length `l` is placed on a smooth table so that one`-`third length hanges freely as shown in the figure. Now the chain is released, with what velocity chain slips off the table?

View SolutionThese diagrams represent the potential energy `U` of a diatomic molecule as a function of the inter-atomic distance `r`. The diagram corresponds to stable molecule found in nature is.
View SolutionThe potential energy of a particle of mass 5 kg moving in the `x-y` plane is given by `U=(-7x+24y)J`, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at `t=2`s is
View SolutionA particle of mass m1 is moving with a velocity `v_(1)` and another particle of mass `m_(2)` is moving with a velocity v2. Both of them have the same momentum but their different kinetic energies are E1 and E2 respectively. If `m_(1) gt m_(2)` then
View SolutionThe potential energy of a certain spring when stretched through a distance 'S' is `10` joule. The amount of work (in joule) that must be done on this spring to stretch it through an additional distance 'S' will be
View SolutionMatch the following
`{: ( "Column I", " Column II"),( "(A)Work", " (p)Slope of (momentum- time)P-t graph") , ("(B) Power " , "(q) Slope of W - t graph"),(" (C)Force" , "(r) Area under F-s graph") , ( "(D)Impulse" , " (iv) Area under F- t graph"):}`
View SolutionWhen a bullet is fired a target, its velocity dwecreases by half after penetrating 30 cm into it. The additional thickness it will penetrate before coming to rest is
View SolutionA bullet of mass `10 gm` is fired horizontally with a velocity `1000 ms^(-1)` from a riffle situated at a height `50 m` above the ground. If the bullet reached the ground with a velocity `500 ms^(-1)`, the work done against air resistance in the trajectory of the bullet is (in joule) `(g = 10 ms^(-2))`.
View SolutionA block of mass `5 kg` is initially at rest on a rough horizontal surface. A force of `45 N` acts over a distance of `2 m`. The force of friction acting on the block is `25 N`. The final kinetic energy of the block is
View SolutionA block of mass `m = 25 kg` on a smooth horizontal surface with a velocity `vec v = 3 ms^(-1)` meets the spring of spring constant `k = 100 N//m` fixed at one end as shown in figure. The maximum compression of the spring and velocity of block as it returns to the original position respectively are.
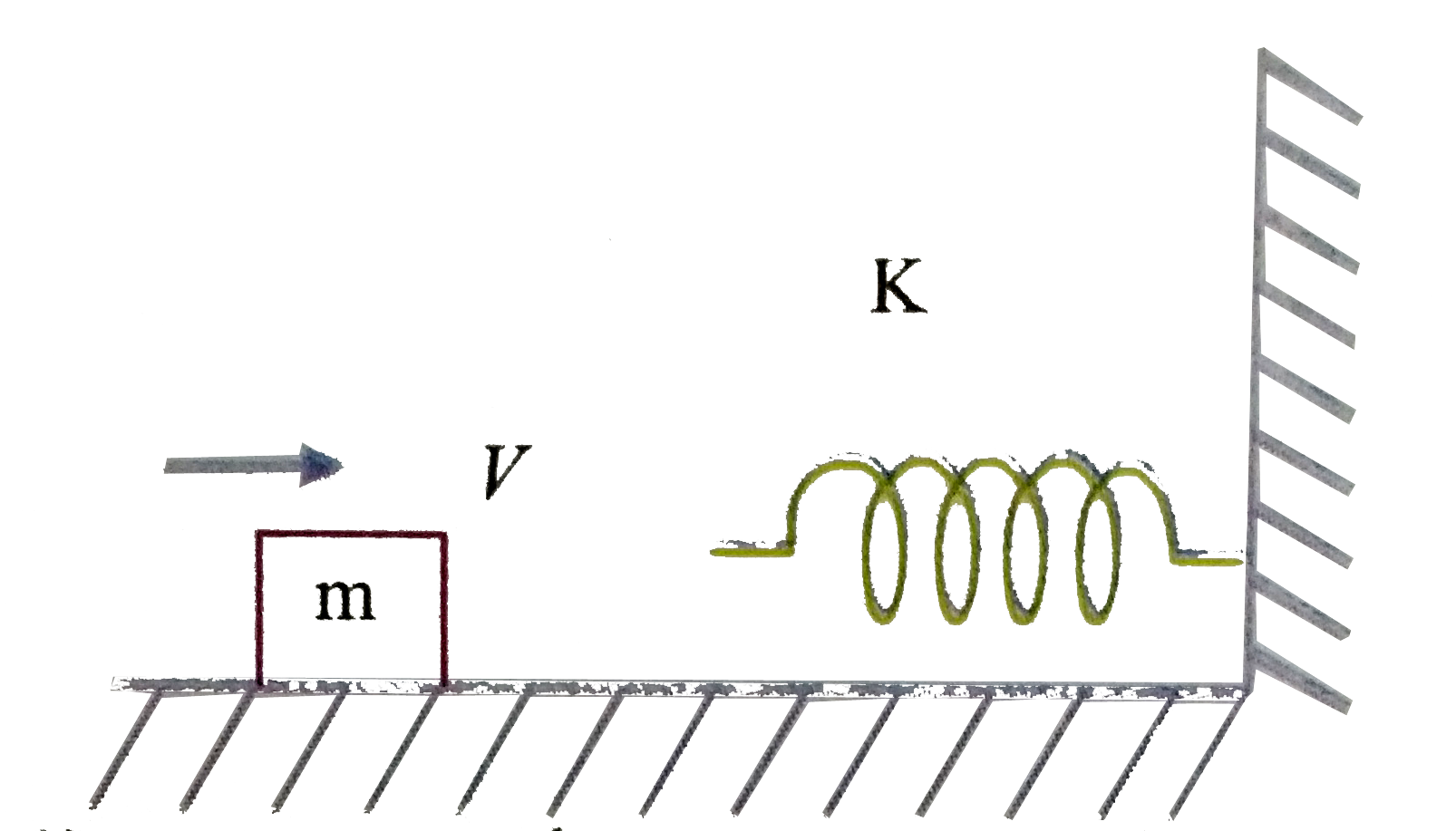 .
.
View SolutionA body freely falls from a certain height onto the ground in a time 't'. During the first one third of the interval it gains a kinetic energy `Delta K_(1)` and during the last one third of the interval, it gains a kinetic energy `Delta K_(2)`. The ratio `Delta K_(1) : Delta K_(2)` is
View SolutionThe potential energy function for the force between two atoms in a diatomic molecule is approximate given by `U(r) = (a)/(r^(12)) - (b)/(r^(6))`, where `a` and `b` are constants and `r` is the distance between the atoms. If the dissociation energy of the molecule is `D = [U (r = oo)- U_("at equilibrium")],D` is
View SolutionThe variation of potential energy U of a body moving along x - axis varies with its position (x) as shown in figure
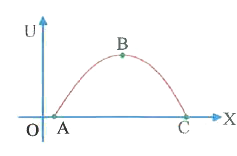
The body is in equilibrium state at
View SolutionThe PE of a 2 kg particle, free to move along x-axis is given by `V(x)=((x^(3))/(3)-(x^(2))/(2))J.` The total mechanical energy of the particle is 4 J. Maximum speed (in `ms^(-1)`) is
View SolutionFigure given below shows the variation of potential energy function U(x), corresponding to one dimensional force field. The point on the graph representing the position of most stable equilibrium is :
` (##NAR_NEET_PHY_XI_P2_C06_E09_112_Q01.png" width="80%">
View SolutionA ball is projected vertically down with an initial velocity from a height of `20 m` onto a horizontal floor. During the impact it loses `50%` of its energy and rebounds to the same height. The initial velocity of its projection is
View SolutionA freely falling body takes `4s` to reach the ground. One second after release, the percentage of its potential energy, that is still retained is
View SolutionTwo identical blocks `A` and `B` , each of mass `m` resting on smooth floor are connected by a light spring of natural length `L` and spring constant `k`, with the spring at its natural length. A third identical block `C` (mass `m`) moving with a speed `v` along the line joining `A` and `B` collides with `A`. The maximum compression in the spring is
View SolutionA body is thrown vertically up with certain initial velocity, the potential and kinetic energies of the body are equal is thrown with double the velocity upwards, the ratio of potential and kinetic energies upwards, the ratio of potential and kinetic energies of the body when it crosses the same point, is
View SolutionA body is thrown vertically upward from a point `A` 125 m above the ground. It goes up to a maximum height of 250 m above the ground and passes through `A` on its downward journey. The velocity of the body when it is at a height of 70 m above the ground is `(g=10 m//s^(2))`
View SolutionA body of mass 10 kg dropped from a height 20 m, acquires a velocity of 10m/s after a falling through a distance of 20m. What is the work done by the air resistance on the body?
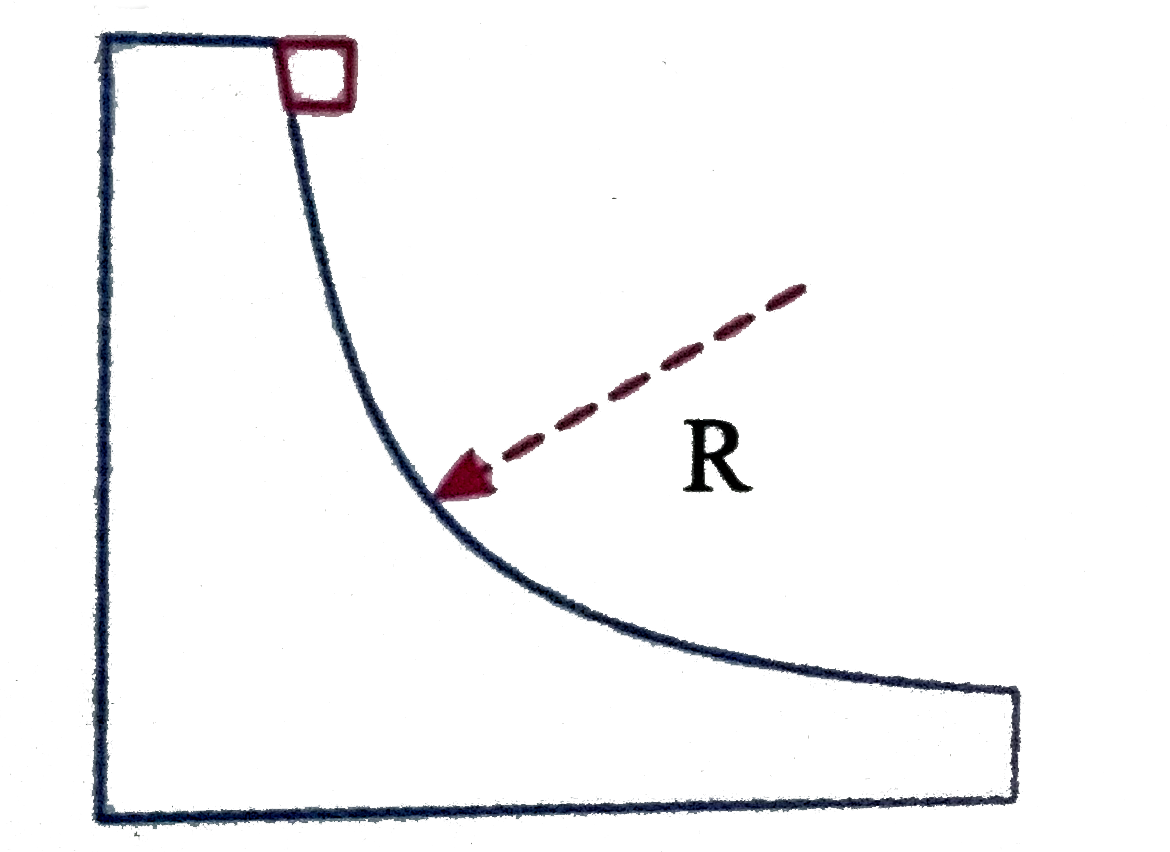
View SolutionA body slides down a fixed curved track that is one quadrant of a circle of radius `R`, as in the figure. If there is no friction and the body starts from rest, its speed at the bottom of the track is
View Solution`AB` is a frictionless inclined surface making an angle of `30^@` with horizontal. A is `6.3 m` above the ground while `B` is `3.8 m` above the ground. A block slides down form `A`, initially starting from rest. Its velocity on reaching `B` is
 .
.
View SolutionA ball of mass`2 kg` and another of mass `4 kg` are dropped together from a `60` feet tall building . After a fall of `30` feet each towards earth , their respective kinetic energies will be the ratio of
View SolutionWhich of the following graphs depicts the variation of `KE` of a ball bouncing on a horizontal floor with height ? (Neglect air resistances)
View SolutionA man `M_(1)` of mass `80 kg` runs up a staircase in `15 s`. Another man `M_(2)` also of mass `80 kg` runs up the same staircase in `20 s`. The ratio of the power development by then will be:
View SolutionA train of weight `10^(7)N` is running on a travel track with uniform speed of `36 km h^(-1)`. The frictional force is 0.5 kg f per quintal. If `g = 10 ms^(-2)`, power of engine is
View SolutionThe velocity 'v' reached by a car of mass 'm' on moving a certain distance from the starting point when driven by a motor with constant power 'P' is such that
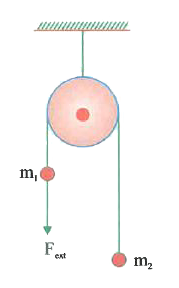
View SolutionTwo bodies of masses `m_(1) and m_(2) (m_(2) gt m_(1))` are connected by a light inextensible string which passes through a smooth fixed pulley. The instantaneous power delivered by an external agent to pull `m_(1)` with constant velocity v is :
View SolutionAn engine pumps water through a hose pipe. Water passes through the pipe and leaves it with a velocity of `2 ms^(1)`. The mass per unit length of water in the pipe is `100 kgm^(-1)`. What is the power of the engine?
View SolutionAn elevator that can carry a maximum load of 1500 kg (elvator+ passengers) is moving up with a constant speed of 2 `ms^(-1).` The frictional force opposing the motion is 3000 N. Find the minmum power delvered by the motor to the elevator in watts as well as in horse power `(g=10ms^(-2))`
View SolutionA particle is projected at `t = 0` from a point on the ground with certain velocity at an angle with the horizontal. The power gravitational force is plotted against time. Which of the following is the best representation ?
View SolutionThe input power to an electric motor is `200 KW`. Its efficiency is `80%`. It operates a crane of efficiency `90%`. If the crane is lifting a load of `3.6` tonnes, the velocity with which the load moves is
View SolutionThe human heart discharges `75 cm^(3)` of blood per beat against an average pressure of `10 cm` of `Hg`. Assuming that the pulse frequency is `75` per minute, the power of the heart is (density of `Hg = 13.6 gm cm^(-3)`)
View SolutionA point size mass `100 gm` is rotated in a vertical circle using a cord of length `20 cm`. When the string makes an angle `60^@` with the vertical, the speed of the mass is `1.5 m//s`. The tangential acceleration of the mass in that position is (in `ms^(-2)`).
View SolutionA vehicle is travelling along concave road then along convex road of same radius of curvatures at uniform speed. If the normal reactions on the vehicle as it crosses the lowest point of concave surface, highest point of convex surface are `1.5 xx 10^(4) N, 3 xx 10^(3) N` respectively, then the mass of vehicle is `(g = 10 m//s^(-2))`.
View SolutionThe length of a simple pendulum is `1 m`. The bob is given a velocity `7 ms^(-1)` in horizontal direction from mean position. During upward motion of bob, if the string breaks when the bob is horizontal, then the maximum vertical height of ascent of bob from rest position is
View SolutionTwo balls marked 1 and 2 of the same mass m and a third ball marked 3 of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball 1 moves with a velocity `v_(1)` towards ball 2. All collisions are assumed to be elastic. If `Mltm`, the number of collisions between the balls will be.

View SolutionA particle of mass `m` moving eastward with a velocity `V` collides with another particle of same mass moving northwards with the same speed `V`. The two particles coalesce and the new particle moves in NE direction. Calculate magnitude and direction of velocity of new particle.
View SolutionA 10 gm bullet is fired from a rifle horizontally into a 5 kg block of wood suspended by a string and the bullet gets embedded in the block. The impact causes the block to swing to a height of `2.5 cm` above its initial level. The velocity of the bullet is
View SolutionThree identical particles with velocities `v_0hati`, `-3v_0hatj` and `5v_0hatk` collide successively with each other in such a way that they form a single particle. The velocity vector of resultant particle is
View SolutionFrom the top of a tower of height `100 m` a `10 gm` block is dropped freely and a `6 gm` bullet is fired vertically upwards from the foot of the tower with velocity `100 ms^(-1)` simultaneously. They collide and stick together. The common velocity after collision is `(g = 10 ms^(-2))`.
View SolutionA steel ball of radius `2 cm` is initially at rest. It is struck head on by another steel ball of radius `4 cm` travelling with a velocity of `81 cm//s`. If the collision is elastic their respective final velocities are
View SolutionA canon shell fired breaks into two equal parts at its highest point. One part retraches the path to the canon with kinetic enegry `E_(1)` and the kinetic energy of the second part is `E_(2)`. Relation between `E_(1)` and `E_(2)` is
View SolutionA mass of 2.9 kg is suspended from a string of length 50 cm and is at rest. Another body of mass 100 g, which is moving horizontally with a velocity of `150 m//s` strikes and sticks to it. Subsequently when the string makes an angle of `60^@` with the vertical, the tension in the string is (g = `10 m//s^(2)`)
View SolutionIn a smooth circular tube of radius `R` , a particle of mass `m` moving with speed `V_(0)` hits another particle of mass `3 m` at rest as shown. The time after which the next collision takes place (assume elastic collision)

View SolutionA mass ‘m’ moves with a velocity ‘v’ and collides inelastically with another identical mass at rest. After collision the 1st mass moves with velocity `(v)/(sqrt(3))` in a direction perpendicular to the initial direction of motion. Find the speed of the `2^(nd)` mass after collision :
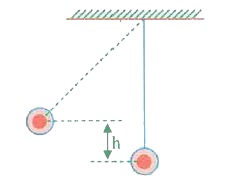
View SolutionIn the figure, pendulum bob on left side is pulled a side to a height h from its initial position. After it is released it collides with the right pendulum bob at rest, which is of the same mass. After the collision the two bobs stick together and raise to a height :-
View SolutionA body oa mass M at rest explodes into three pieces, two of which of mass (M/4) each are thrown- off in perpendicular directions with velocities of ` 6 ms^(-1)` and `8 ms^(-1)` respectively. The third piece will be thrown-off with a velocity of `
View SolutionA mass `m` moving horizontal (along the x-axis) with velocity `v` collides and stricks to mass of `3m` moving vertically upward (along the y-axis) with velocity `2v`. The final velocity of the combination is
View SolutionDuring "elastic collision"
a) there is no loss of kinetic energy
b) the bodies are perfectly elastic
c) temporarily some of the kinetic energy is used to deform the bodies
d) after collision the bodies regain the original shape keeping the total energy constant
View SolutionIdentify the correct statements from the following
a) the collisions between the nuclei and fundamental particles are considered as elastic collisions
b) Emission of an alpha particle by a heavy nucleus is an "elastic collision"
c) The collision between two ivory balls is considered as "elastic collision"
d) A running man jumps into a train. It is an "elastic collision"
View SolutionA ball hits a floor and rebounds after an inelastic collision. In this case
View Solution
EXERCISE -II (H.W) questions and complete solutions for chapter WORK , ENERGY & POWER of NARAYANA PHYSICS (HINGLISH) of Class 11