Complete Solutions to EXERCISE -II (C.W) of chapter WORK , ENERGY & POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK , ENERGY & POWER |
| NARAYANA | EXERCISE -II (C.W) |
| Number Of Questions | 75 |
| Academic Year | 2023-24 |
A particle is moved from (0, 0) to (a, a) under a force a `F=(3hat(i)+4hat(j))` from two paths. Path 1 is OP and path 2 is OPQ. Let `W_(1)` and `W_(2)` be the work done by this force in these two paths. Then,
View SolutionThe graph betwee `sqrt(E)` and `(1)/(p)` is (E=kinetic energy and p= momentum)
View SolutionA body of mass `3 kg` is under a constant force which causes a displacement `s` metre in it, given by the relation `s=(1)/(3)t^(2)`, where `t` is in seconds. Work done by the force in 2 seconds is
View SolutionA person used force `(F)` , shown in figure to move a load with constant velocity on given surface. Identify the correct surface profile:
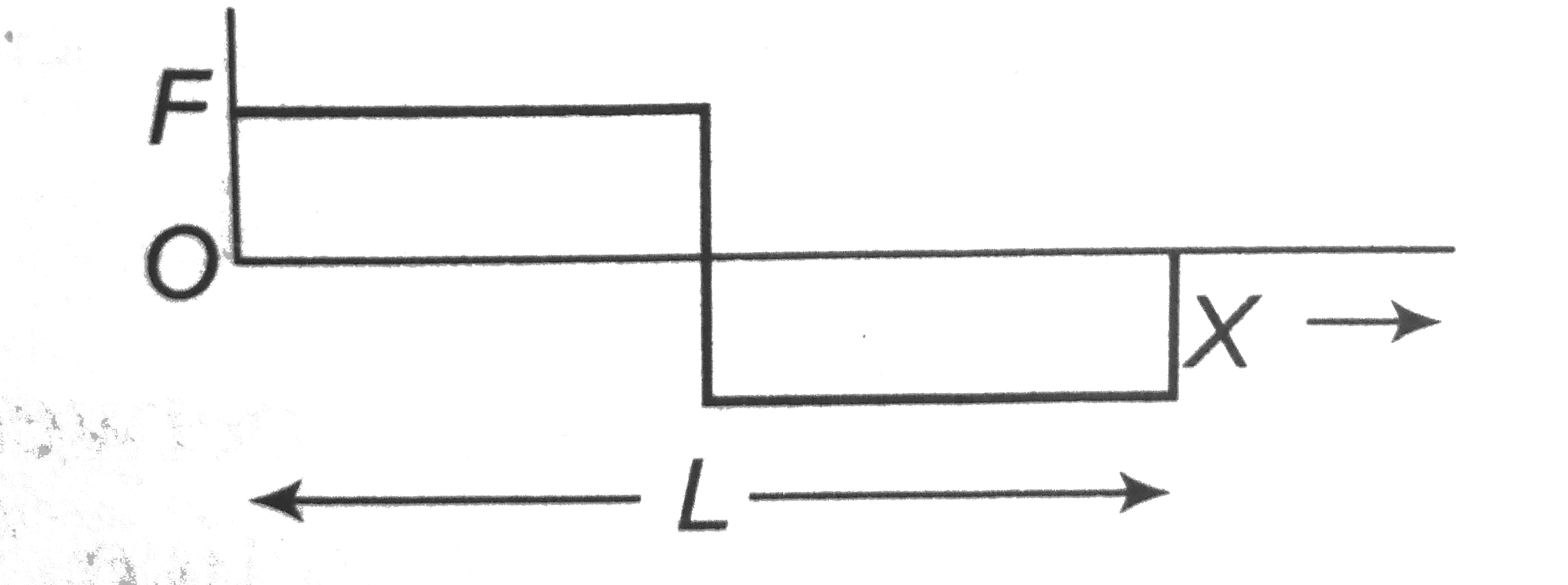
View SolutionA bucket of mass `'m'` tied to a light rope is lowered at a constant acceleration of `g//4`. IF the bucket is lowered by a distance `'d'` , the work done by the rope will be (neglect the mass of the rope)
View SolutionWater is drawn from a well in a `5kg` drum of capacity `55L` by two ropes connected to the top of the drum. The linear mass density of each rope is `0.5kgm^-1`. The work done in lifting water to the ground from the surface of water in the well `20m` below is
`[g=10ms^-2]`
View SolutionA block of mass `10 kg` slides down a rough slope which is inclined at `45^(0)` to the horizontal. The coeffficient of sliding friction is `0.30`. When the block has to slide `5m`, the work done on the block by the force of friction is nearly
View SolutionA uniform rope of length `'L` and linear density `'mu'` is on a smooth horizontal table with a length `'l'` lying on the table. The work done in pulling the hanging part on to the table is
View SolutionA long rod `ABC` of mass "m" and length "L" has two particles of masses "m" and "2m" attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with `A` hinged at the bottom is
 .
.
View SolutionA particle of mass `0.5kg` travels in a straight line with velocity `v=ax^(3//2)` where `a=5m^(-1//2)s^-1`. What is the work done by the net force during its displacement from `x=0` to `x=2m`?
View SolutionA block of mass M is kept on a platform which starts accelerating upwards from rest with a constant acceleration a. During the time interval T, the work done by contact froce on mass M is
` (##NAR_NEET_PHY_XI_P2_C06_E09_011_Q01##) `
View SolutionIn the figure shown all the surfaces are frictionless, and mass of the block 'm' is 1 kg. The block and wedge are held initially at rest. Now wedge is given a horizontal acceleration of `5 m/s^(2)` by applying a force on the wedge, so that the block does not slip on the wedge. Then work done by the normal force in ground frame on the block in 2 sec is :
` (##NAR_NEET_PHY_XI_P2_C06_E09_012_Q01.png" width="80%">
View SolutionThree components of a force acting on a particle are varying according to the graphs as shown. To reach at point B(8, 20, 0)m from point A(0, 5, 12)m the particle moves on paths parallel to x-axis then y-axis and then z-axis, then work done by this force is:
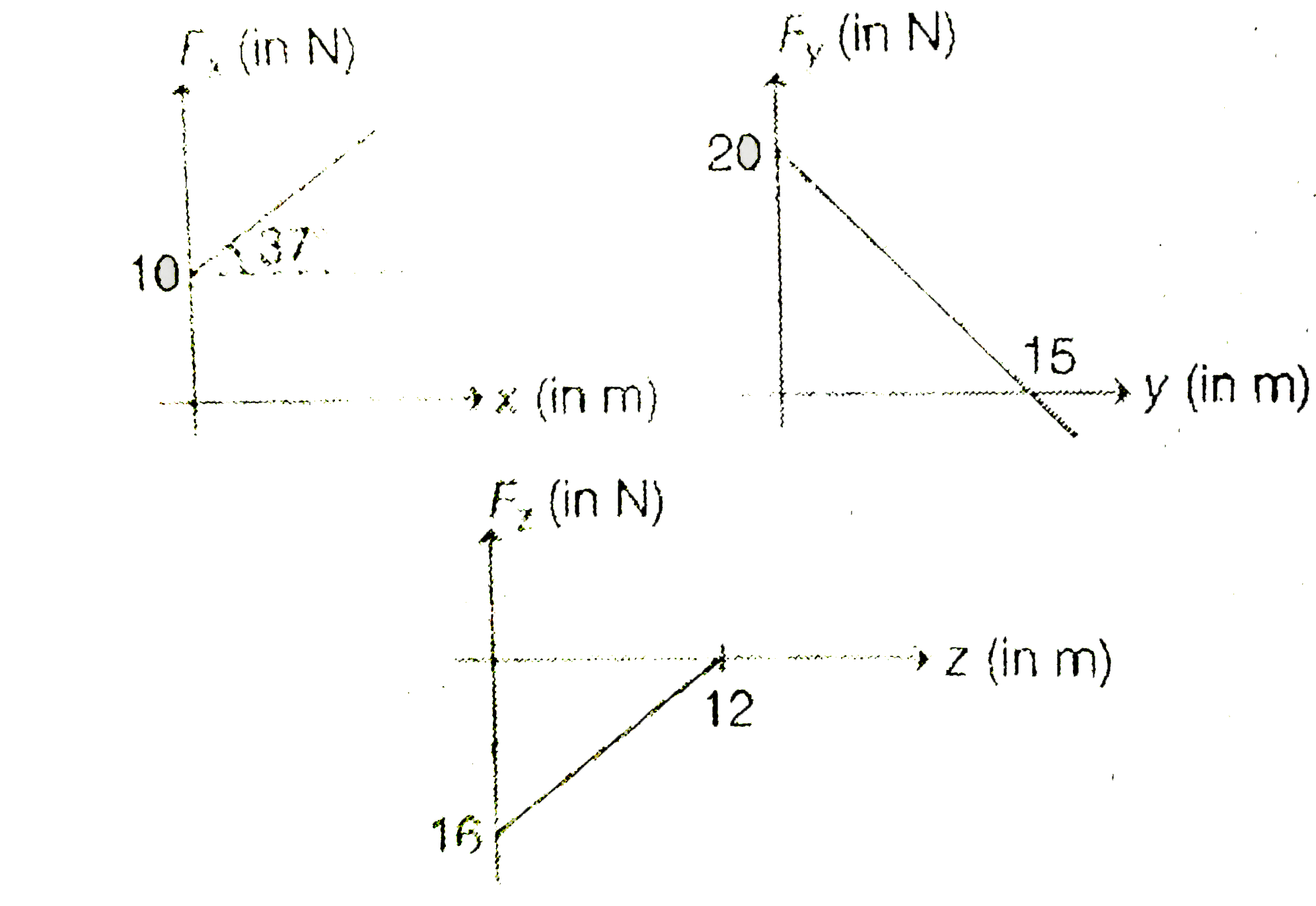
View SolutionA force `vec F = (3 vec i + 4vec j)N`, acts on a particle moving in x-y plane. Starting from origin, the particle first goes along x-axis to thepoint (4,0)m and then parallel to the y -axis to the point(4, 3)m. The total work done by the force on the particle is
` (##NAR_NEET_PHY_XI_P2_C06_E09_014_Q01.png" width="80%">
View SolutionTwo inclined frictionless tracks, one gradual and other steep meet at 'A' from where two stones are allowed to slide down from rest, one on each track as shown in figure. The speed of two stones on reaching at bottom are `v_(1) and v_(2)` respectively. `v_(1) & v_(2)` are related as
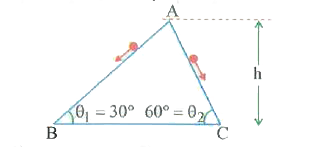
View SolutionTwo spheres of same material are moving with kinetic energies in the ratio `108:576`. If the ratio of their velocities is `2:3`, then the ratio of their radii is
View SolutionIf the mass of a moving body decreased by one third of its initial mass and velocity is tripled, then the percentage change in its kinetic energy is
View SolutionThe kinetic energy of a moving body is given by `k = 2v^(2), k` being in joules and `v` in `m//s`. It's momentum when travelling with a velocity of `2m//s` will be (in `kg ms^(-1)`)
View SolutionThe kinetic energy (KE) versus time graph for a particle moving along a straight line is as shown in the figure. The force versus time graph for the particle may be
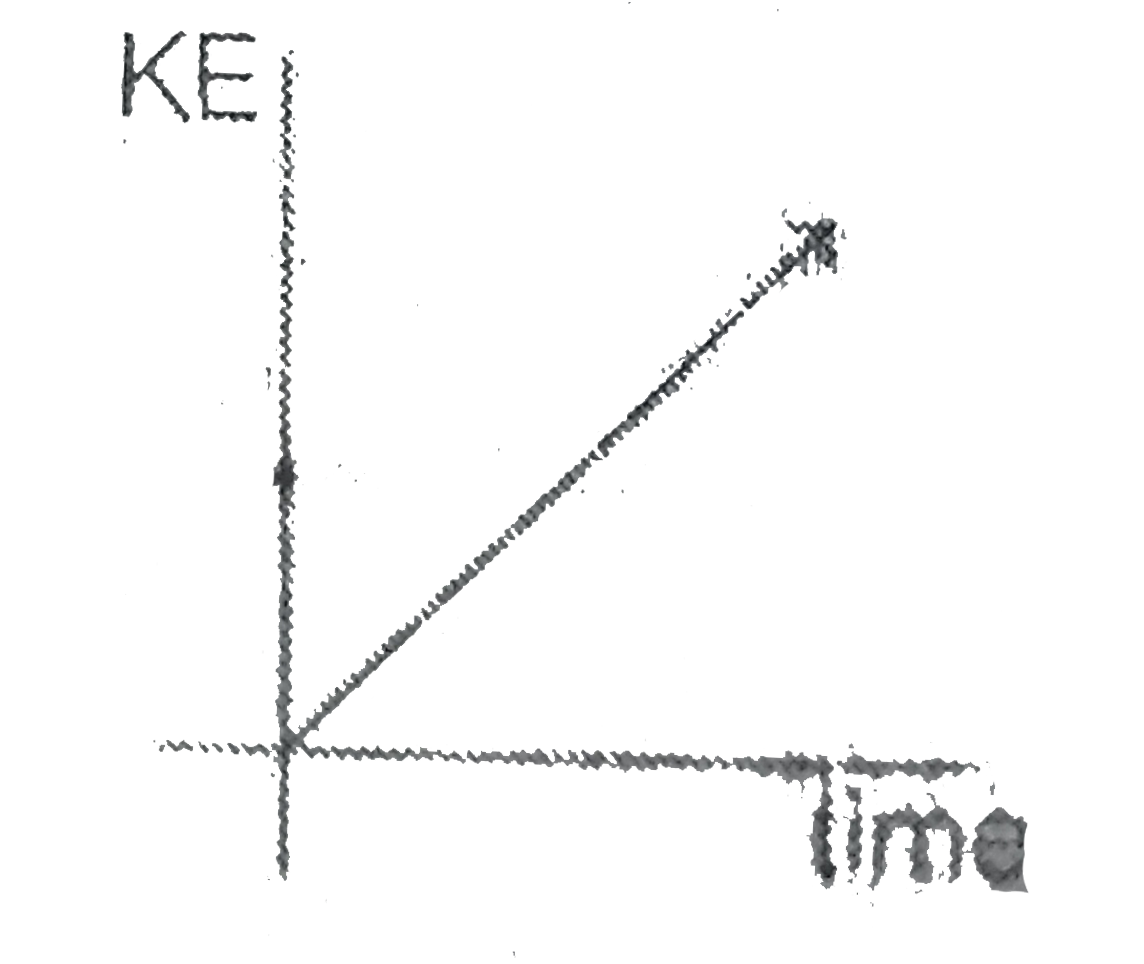
View SolutionA uniform chain of length 2 m is kept on a table such that a length of 60 cm hangs freely from the edge of the table. The total mass of the chain is 4 kg. What is the work done in pulling the entire chain on the table?
View SolutionThe potential energy of a body mass m is `U=ax+by` the magnitude of acceleration of the body will be-
View SolutionA block of mass M is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic energy of the block increases by 20 J in 1 s:-
View SolutionThe kinetic energy K of a particle moving along x - axis varies its position (x) as shown in figure.

The magnitude of force acting on particle at x = 9m is
View SolutionFigure given below shows the plot of the conservative force F, in a unidimensional field. The plot representing the function corresponding to the potential energy (U) in the field is :
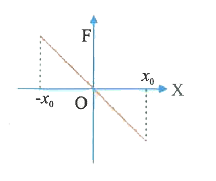
View SolutionMatch the following
`{: ( "Column I", " Column II"),(" (A) Example of conservative force ", "(p) Work done by all forces " ) ,("(B) Potential energy defined for only " , "(q) Force constant (spring constant)"), ("(C ) If two spring are stretched by same force, then ratio of their potential energy is in the inverse ratio of their " , "(r) Gravitational force"),("(D) Change in kinetic energy is equal ", "(s) Conservative force"):}`
View SolutionA massless spring with a force constant `K = 40N//m` hangs vertically from the ceiling.A `0.2 kg` block is attached to the end of the spring and held in such a position that the spring has its natural length and suddenly released. The maximum elastic strain energy stored in the spring is `(g=10 m//s^(2))`
View SolutionA block of mass m moving at a speed v compresses as spring thrugh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA bead of mass `1/2 kg` starts from rest from A to move in a vertical place along a smooth fixed quarter ring of radius `5 m`, under the action of a constant horizontal force `f=5 N` as shown. The speed of bead as it reaches the point (B) is [Take `g=10 ms^(-2)`]
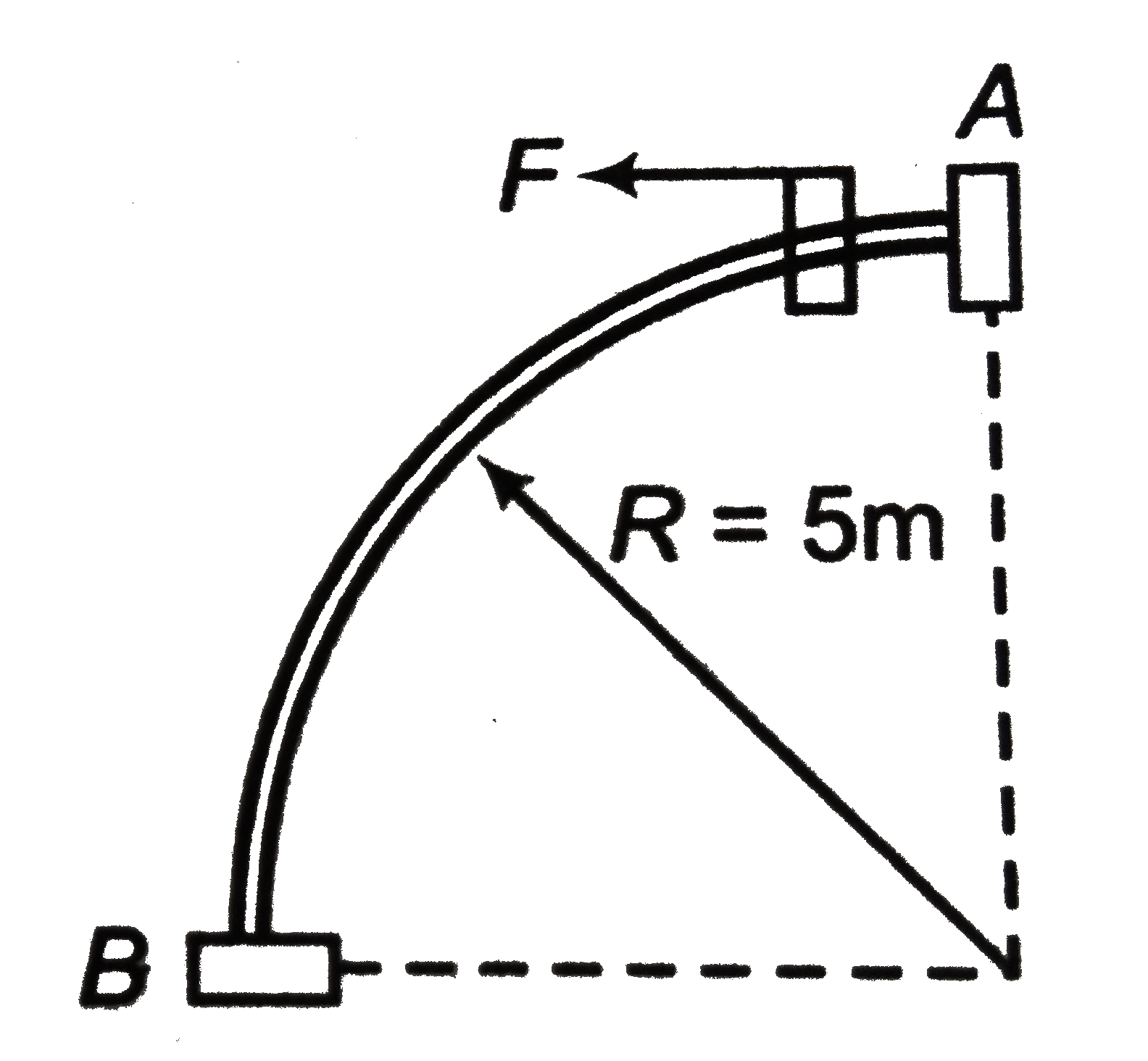
View SolutionAn outfielder throws a cricket ball with an initial kinetic energy of `800 J` and an infielder catches the ball when its kinetic energy is `600 J`. If the path of the ball between them is assumed straight and is `20 m` long, the air resistance acting on the ball is
View SolutionVelocity-time graph of a particle of mass (2 kg) moving in a straight line is as shown in Fig. 9.20. Find the word done by all the forces acting on the particle.
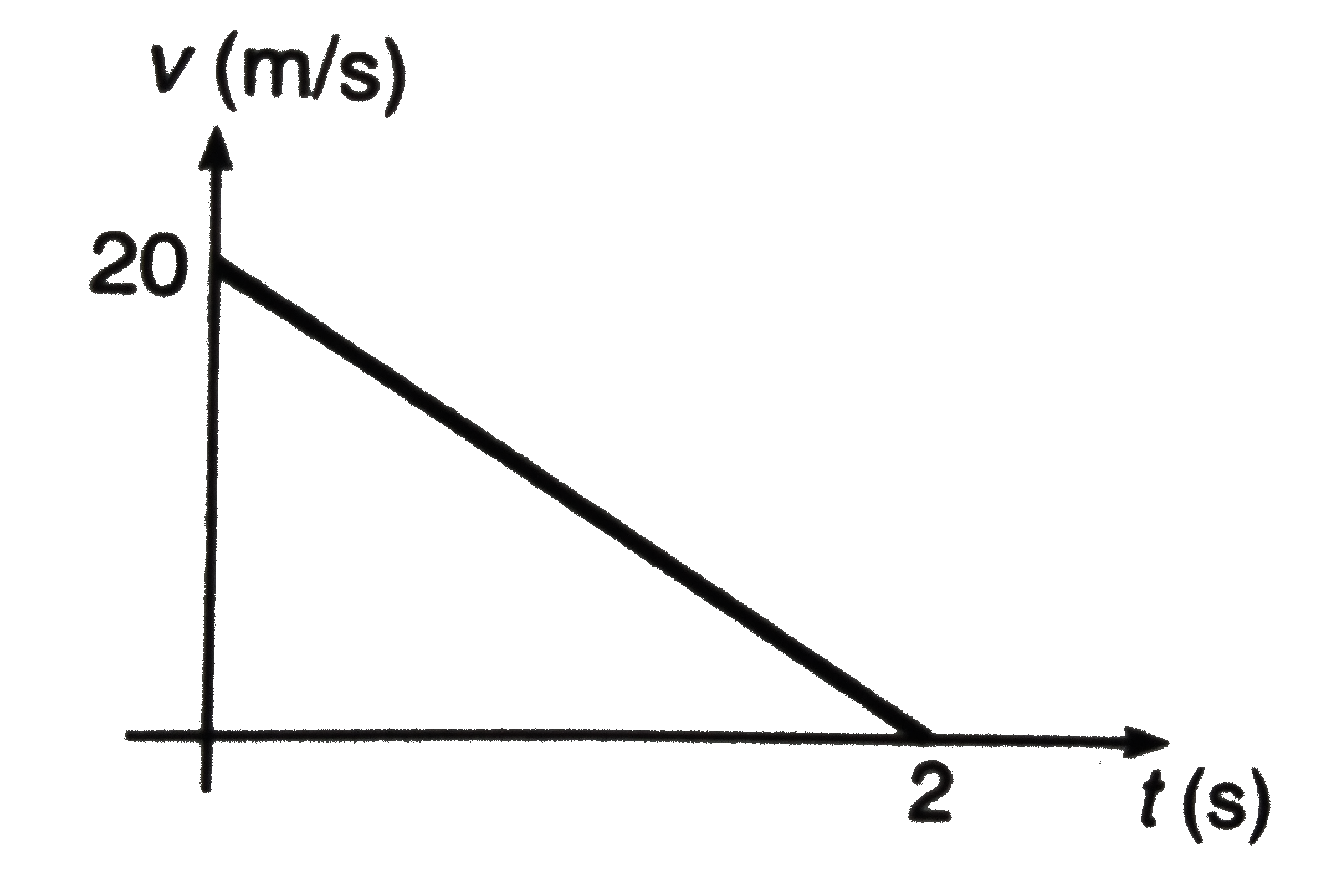 .
.
View SolutionA block of mass 1 kg slides down a vertical curved track that is one quadrant of a circle of radius 1m. Its speed ast the the bottom si `2 m//s`. The work done by frictional force is :

View SolutionA force `F = Ay^(2)+By+C` acts on a body at rest in the `Y`-direction. The kinetic energy of the body during a displacement `y = -a` to `y = a` is
View SolutionA block of mass `m=1kg` moving on a horizontal surface with speed `v_(i)=2ms^(-1)` enters a rough patch ranging from `x0.10m to x=2.01m`. The retarding force `F_(r)` on the block in this range ins inversely proportional to x over this range
`F_(r)=-(k)/(x) fo r 0.1 lt xlt 2.01m`
`=0` for `lt 0.1m` and `x gt 2.01m` where `k=0.5J`. What is the final K.E. and speed `v_(f)` of the block as it crosses the patch?
View SolutionIn the fig. The potential energy U of a particle plotted against its position x from origin. Which of the following statement is correct
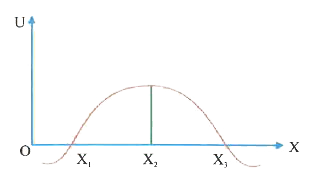
View SolutionIf `F = 2x^(2) - 3x -2`, then choose correct option:-
View SolutionThe potential energy of a 1kg particle free to move along the x-axis is given by `V(x)=(x^(4)/4-x^(2)/2)J` The total mechanical energy of the particle is 2J then the maximum speed `(in m//s)` is
View SolutionA particle located in one dimensional potential field has potential energy function`U(x)=(a)/(x^(2))-(b)/(x^(3))`, where a and b are positive constants. The position of equilibrium corresponds to x equal to
View SolutionA block of mass 30.0 kg is being brought down by a chain. If the block acquires as speed of `40.0 `cm/s` in dropping down 2.00 m ,find the work done by the chain during the process.
View SolutionA body of mass 2 kg is thrown vertically upwards with K.E of 245 J. The acceleration due to gravity is `9.8 ms^(-2)`. The K.E. Of the body will become half at the height of
View SolutionA `3kg` model rocket is launched striaght up with sufficient initial speed to reach a maximum height of `100 m`, even though air resistance (a non-conservative force) performs -`900 J` of work on the rocket. The highest the rocket would have gone without air resistance will be
View SolutionIn the arrangement shown in figure, string is light and inextensible and friction is absent every where. The speed of both blocks after the block `'A'` has ascend a height of `1m` will be `(g=10 m//s^(2))`
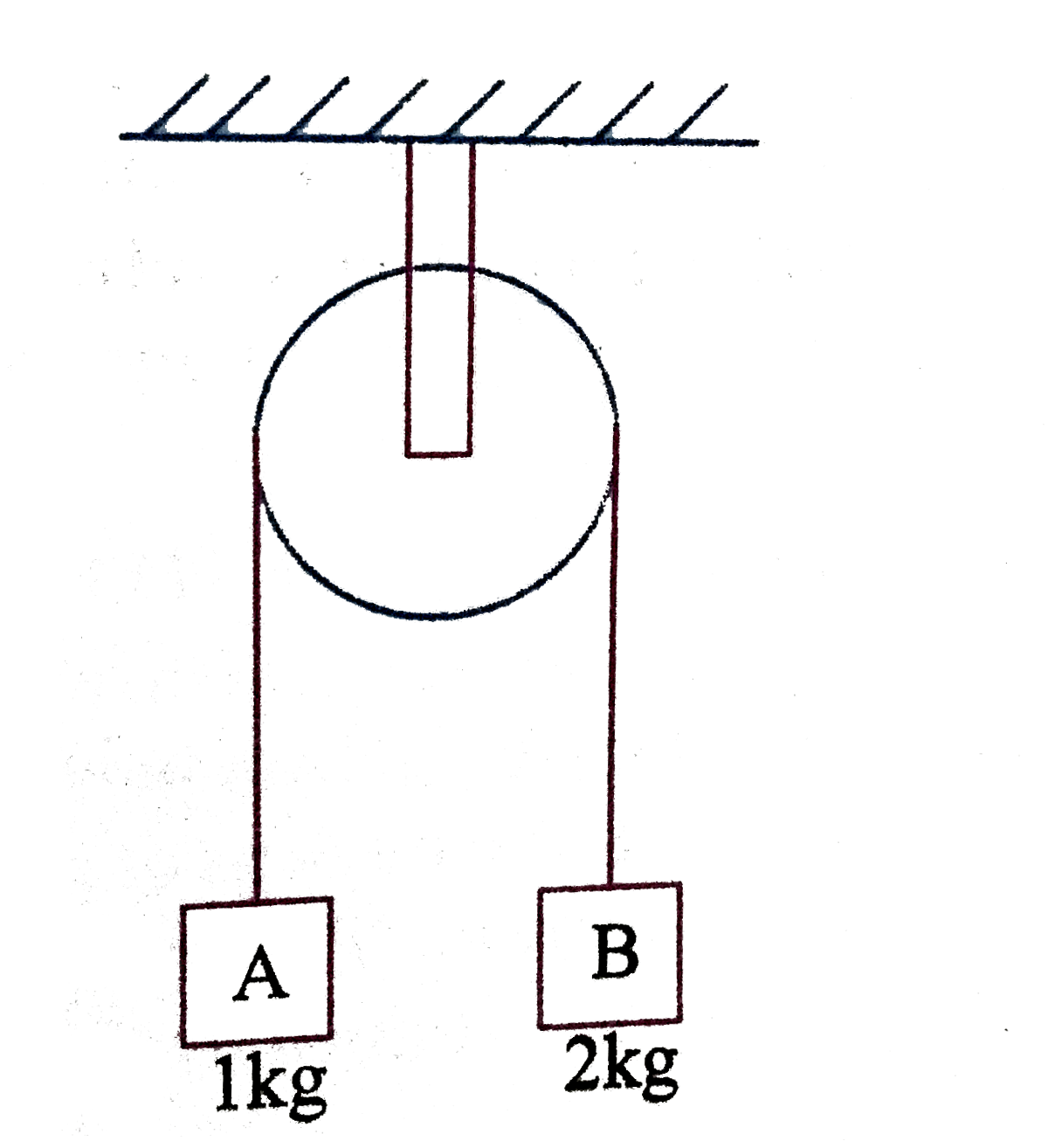
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5m, what is the speed with which the bob arrive at the lower most point, given that, it dissipated 5% of its initial energy against air resistance?
View SolutionSystem shown in figure is released from rest . Pulley and spring is mass less and friction is absent everywhere. The speed of `5 kg` block when `2 kg` block leaves the constant of with ground is (force constant of spring `k = 40 N//m and g = 10 m//s^(2))`

View SolutionThe potential energy of a particle of mass `m` is given by `U = (1)/(2) kx^(2)` for `x lt 0` and `U=0` for `x ge 0`. If total mechanical energy of the particle is `E`. Then its speed at `x = sqrt((2E)/(k))` is
View SolutionFigure shows the vertical section of a frictionless surface. A block of mass `2kg` is released from rest from position A, its KE as it reaches position C is (`g=10ms^-2`)
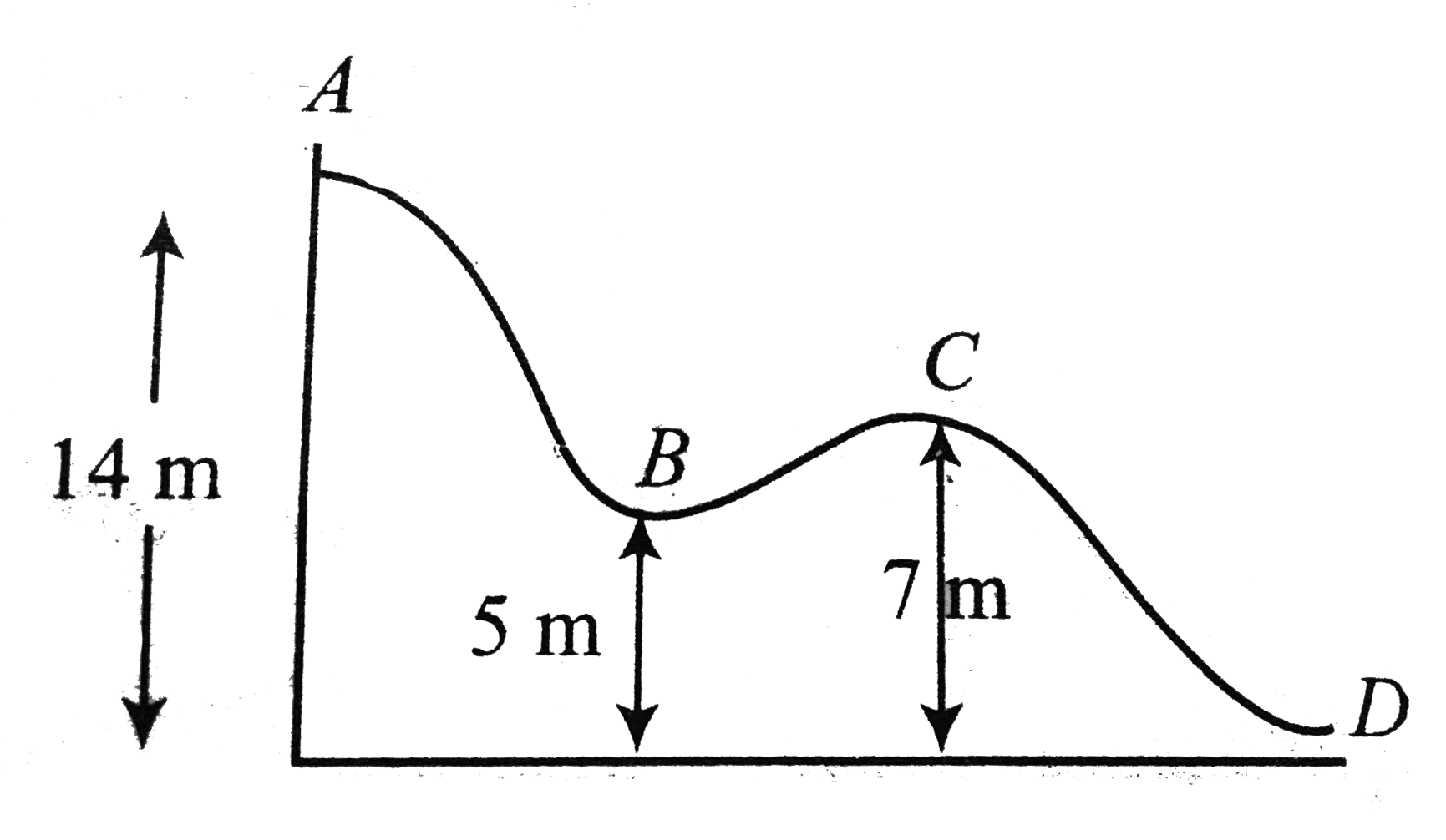
View SolutionA body of mass `m` falls from a height `h` and collides with another body of same mass at rest. After collision, the two bodies combine and move through distance `(d)` till they come to rest. Find the work done against the resistive force.
View SolutionPower supplied to a particle of mass 4 kg varies with time as `P=(3t^(2))/(2)` watt. Here t in second. If velocity of particle at t = 0 is v = 0, the velocity of particle at time t = 2s will be
View SolutionA particle of mass m is moving in a circular path of constant radius r such that its centripetal acceleration `a_(c)` is varying with time t as `a_(c) = k^(2)rt^(2)`, where k is a constant. The power delivered to the particle by the forces acting on it is :
View SolutionA constant power `P` is applied to a particle of mass `m`. The distance traveled by the particle when its velocity increases from `v_(1)` to `v_(2)` is (neglect friction):
View SolutionA body is moved from rest along a straight line by a machine delivering constant power. The ratio of displacement and velocity `(s//v)` varies with time `t` as
View SolutionPower applied to a particle varices with time as `P =(3t^(2)-2t + 1)` watt, where t is in second. Find the change in its kinetic energy between time `t=2s` and `t = 4 s` .
View SolutionA car of mass `M` accelerates starting from rest. Velocity of the car is given by `v=((2Pt)/(M))^((1)/(2))` where `P` is the constant power supplied by the engine. The position of car as a function of time is given as
View SolutionPower supplied to a particle of mass 4 kg varies with time as `P=(3t^(2))/(2)` watt. Here t in second. If velocity of particle at t = 0 is v = 0, the velocity of particle at time t = 2s will be
View SolutionA particle is moving along x-axis under the action of a force F, which varies with its position `(x)as fprop(1)/(sqrtx).`Find the variation of power due to this force with x.
View SolutionA body of mass m is projected with intial speed u at an angle `theta` with the horizontal. The change in momentum of body after time t is :-
View SolutionA stone is tied to a string of length l and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is
View SolutionA simple pendulum is oscillating with angular displacement `90^(@)` For what angle with vertical the acceleration of bob direction horizontal?
View SolutionA nail is fixed at a point `P` vertically below the point of suspension 'O' of simple pendulum of length `1 m`. The bob is released when the string of pendulum makes an angle `30^@` with horiozontal. The bob reaches lowest point and then describes vertical circle whose centre coincides with `P` . The least distance of `P` from `O` is
View SolutionA simple pendulum with a bob of mass 'm' swings with angular amplitude of `60^@`. When its angular displacement is `30^@`, the tension in the strings would be
View SolutionA stone of mass 1 kg tied to a light inextensible string of lenth `L=(10)/(3)m`, whirling in a circular path in a vertical plane. The ratio of maximum tension to the minimum tension in the string is 4. If g is taken to be `10ms^(-2)`, the speed of the stone at the highest point of the circle is
View SolutionA stationary body explodes into two fragments of masses `m_(1)` and `m_(2)`. If momentum of one fragment is `p`, the energy of explosion is
View SolutionA mass of 1 kg is thrown up with a velocity of 100 m/s. After 5 seconds. It explodes into two parts. One parts of mass 400 g comes down with a velocity 25 m/s Calaculate the velocity of other parts:
View SolutionA bob is suspended from a crane by a cable of length `l=5 m`. The crane and load are moving at a constant speed `v_(0)`. The crane is stopped by a bumper and the bob on the cable swings out an angle of `60^(@)`. The initial speed `v_(0)` is `(g=9.8 m//s^(2))`
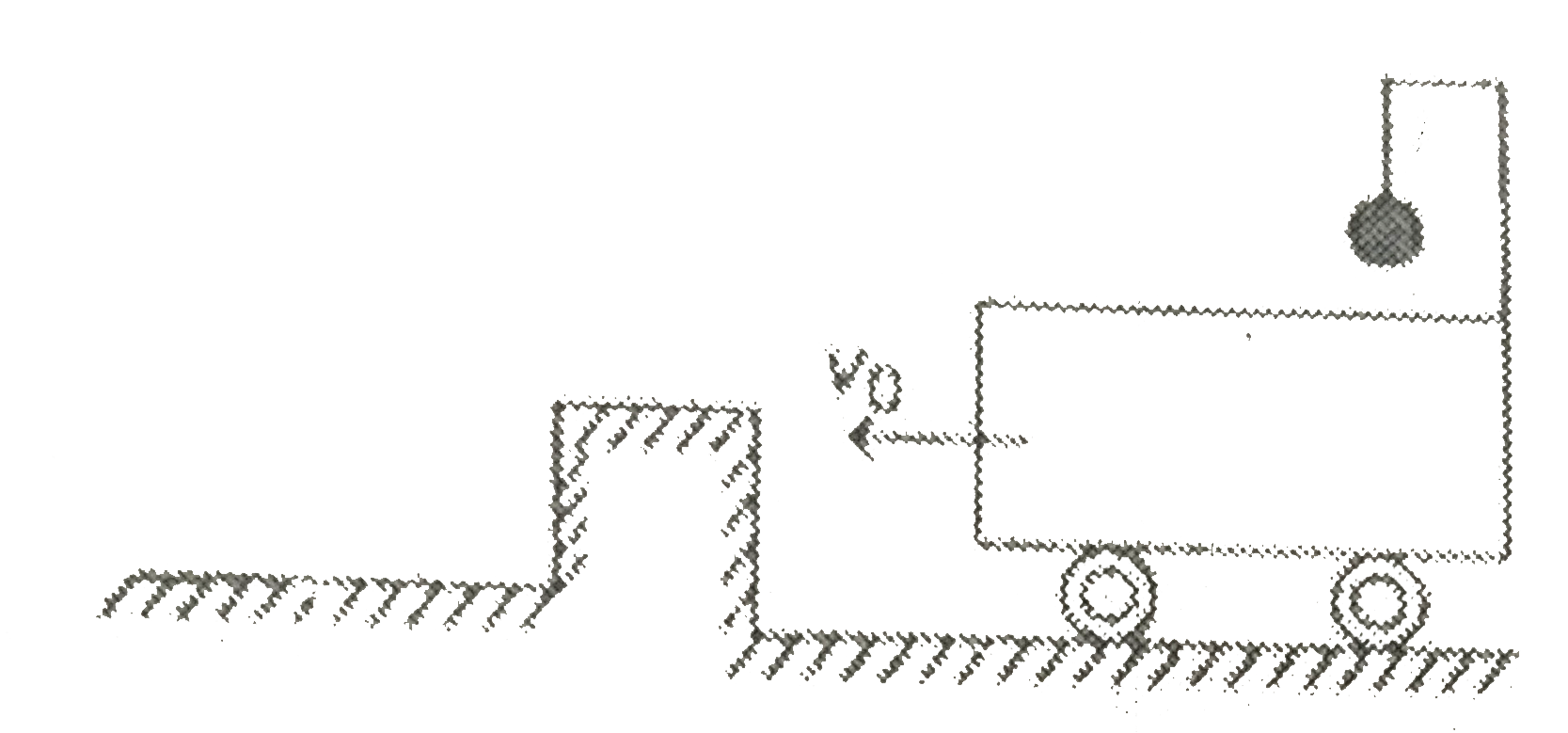
View SolutionTwo balls each of mass `'m'` are moving with same velocity `v` on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionA block of wood of mass `3M` is suspended by a string of length `(10)/(3) m`. A bullet of mass `M` hits it with a certain velocity and gets embedded in it. The block and the bullet swing to one side till the string makes `120^@` with the initial position. the velocity of the bullet is `(g=10 ms^(-2))`.
View SolutionAt high altitude , a body explodes at rest into two equal fragments with one fragment receiving horizontal velocity of `10 m//s`. Time taken by the two radius vectors connecting of explosion to fragments to make `90^(@)` is
View SolutionThree particles A, B and C of equal mass move with equal speed V along the medians of an equilateral triangle as shown in hgure. They collide at the centroid G of the triangle. After the collision, A comes to test, B retraces its path with the speed V. What is the velocity of C ?
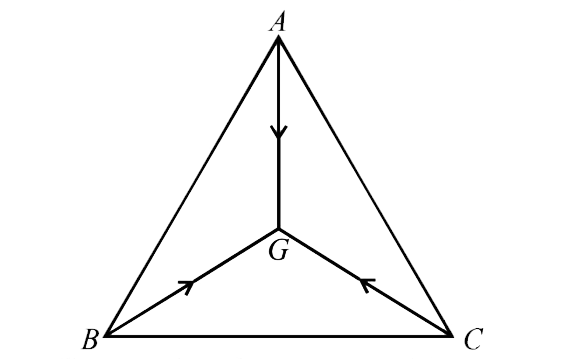
View SolutionTwo sphere `A` and `B` of equal masses lie on the smooth horizontal circular groove at opposite ends of diameter and at the end of time 't','A' impings on 'B' . If 'e' is the coefficient of restitution, the second impinge will occur after a time
View SolutionA mass of `2.9 kg` is suspended from a string of length `50 cm` and is at rest . Another body of mass `100 gm` which is moving horizontal with a velocity of `150 m//s` strikes it . After striking the two bodies combine together . Tension in the string , when it is at an angle of `60^(@)` with the velocity is : `g = 10 m//s^(2)`
View SolutionA block 'A' of mass M moving with speed u collides elastically with block B of mass m which is connected to block C of mass m with a spring. When the compression in spring is maximum, the velocity of block C with respect to block A is (neglect friction) :-

View SolutionA ball moving with velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at an angle of `30^(@)` with the original line of motion. What are the speeds of the balls after the collision ?
View SolutionTwo identical balls `A` and `B` are released from the position shown in Fig. They collide elastically with each other on the horizontal portion. The ratio of heights attained by `A` and `B` after collision is (neglect friction)

View SolutionA billiards player hits a stationary ball by an identical ball to pocket the target ball in a corner pocket that is at an angle of `35 ^(@)` with respect to the direction of motion of the first ball. Assuming the collision as elastic and that friction and rotational motion are not important, the angle made by the target ball with repect to the incoming ball is
View SolutionStatement -I : If collision occurs between two elastic bodies their kinetic energy decreases during the time of collision.
Statement -II : During collision intermolecular space decreases and hence elastic potential energy increases
View SolutionAssertion: A quick collision between two bodies is more violent that show collision , even when initial and final velocity are identical.
Reason: The rate of change of momentum determine that force is small or large.
View Solution
EXERCISE -II (C.W) questions and complete solutions for chapter WORK , ENERGY & POWER of NARAYANA PHYSICS (HINGLISH) of Class 11