Complete Solutions to EXERCISE of chapter MOTION IN A STRAIGHT LINE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A STRAIGHT LINE |
| NCERT | EXERCISE |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
In which of the following exmples of motion, can the body be considered approxinmately a point object :
(a) a railway carriage moving without jerks between two two stations.
(b) a mondey sistting on top of a man cycling smoothly on a circulat track. (c ) a spinning cricket ball that turns sharply on hitting the round . (d) a tumbling beake theat has slopped off the edge of a table ?
View Solution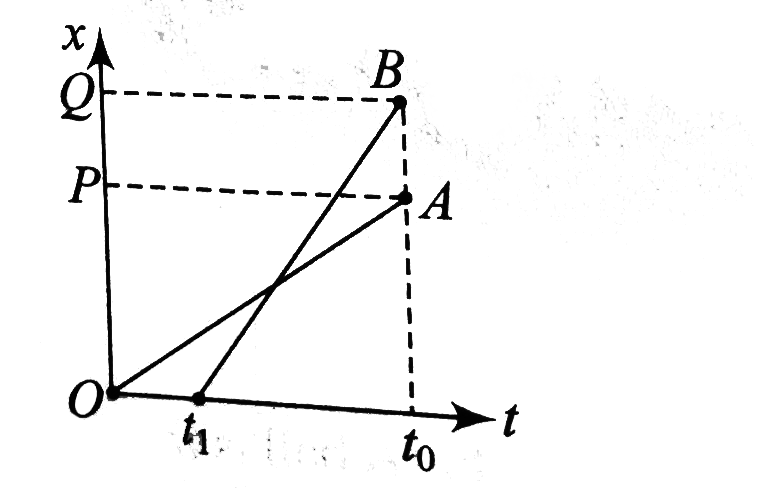
The position-time (x-t) graphs for two children A and B returning from their school O to their homes P and Q respectively along straight line path (taken as x-axis) are shown in figure. Choose the correct statement (s):
View SolutionA woman starts from her home at `9.00` a.m., walks with a speed of `5 km h^(-1)` on straight road up to her office `2.5 km` away, stays at the office up to `5.00 p.m.`, and returns home by an auto with a speed of `25 kmh^(-1)`. Plot the position-time graph of the woman taking home as origin.
View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the `x -t` graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start
View SolutionA jet airplane travelling at the speed of ` 500 km ^(-1)` ejects its products of combustion at the speed of ` 1500 km h^(-1)` relative to the jet plane. What is the speed of the burnt gases with respect to observer on the ground ?
View SolutionA car moving along a straight highway with speed of ` 126 km h^(-1)` is brought to a stop within a distance of ` 200 m`. What is the retardation of the car (assumed uniform) and how long does it take for the car to stop ?
View SolutionTwo trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of `72 km h^(-1)` in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by `1 ms^(-2)`. If after 50s, the guard of B just brushed past the driver of A, what was the original distance between them ?
View SolutionOn a two lane road , car (A) is travelling with a speed of `36 km h^(-1)`. Tho car ` B and C` approach car (A) in opposite directions with a speed of ` 54 km h^(-1)` each . At a certain instant , when the distance (AB) is equal to (AC), both being ` 1 km, (B) decides to overtake ` A before C does , What minimum accelration of car (B) is required to avoid and accident.
View SolutionTwo towns `A` and `B` are connected by a regular bus service with a bus leaving in either direction every `T` min. `A` man cycling with a speed of `20 km h^(-1)` in the direction `A` to `B` notices that a bus goes past him every `18 min` in the direction of his motion, and every `6 min` in the opposite direction. What is the period `T` of the bus service and with what speed (assumed constant )do the buses ply on the road?
View SolutionA player throwsa a ball upwards with an initial speed of `29.4 ms^(-1)`.
(i) What is the direction of acceleration during the upwared motion of the ball?
(ii) What are the velocity and acceleration of the ball at the highest point of its motion?
(iii) Choose the x=0 and t=0 to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of X-axis, and give the signs of positive, velocity and acceleration of the ball during its upward, and downward motion.
(iv) To what height does the ball rise and after how long does the ball return to the player's hand?( Take g`=9.8 ms^(-2)`, and neglect air resistance).
View SolutionRead each statement below carefully and state with reasons and examples if it is true or false ,
(a) with zero speed at an instant may have non-zero acceleration at that instant
(b) with zero speed may have non-zero velocity
(c ) with positive constant speed must have zero acceleration
(d) with positive value of acceleration must be speeding up.
View SolutionA ball is dropped from a height of a height of 90 m on a floor. At each collsion with the floor , the ball loses one - tenth of its speed . Plot the speed -time graph of its motion between t 0 to 12 s.
View SolutionExplain clearly, with ezamples, the difference between :
(a) magnitude of displacemnt (sometimes called distance ) overand
interval of time, and the total length of the path coverd by a particle over the same interval.
(b) magnitude of average velocity over an intercal of time , and the average speed
over the same interval. [ Average speed of a particle over an interval of time is defined as the toal path length
divided by the time intrval]. Show in both (a) and (b) that the second quantity is either greater than or equal to first.
When is the equality sing true ? [ For simplocity, consider one- dimensional motion only]
View SolutionA man walks on a straight road from his home to a market ` 2.5 km` away with a speed of `5 km //h`. Finding the market closed, he instantly turns and walks back with a speed of `7.5 km//h`. What is the (a) magnitude of average velocity and (b) average speed of the man, over the interval of time (i) `0` to 30 min `. (ii) 0 to 50 min (iii) 0 to 40 min ?
View SolutionThe instantaneous speed is always equal to the magnitude of instantaneous velocity. Why?
View SolutionLook at the graphs (a) to (d) carefully and state, with reasons, with of these cannot possibly represent one dimensional motion of a particle.
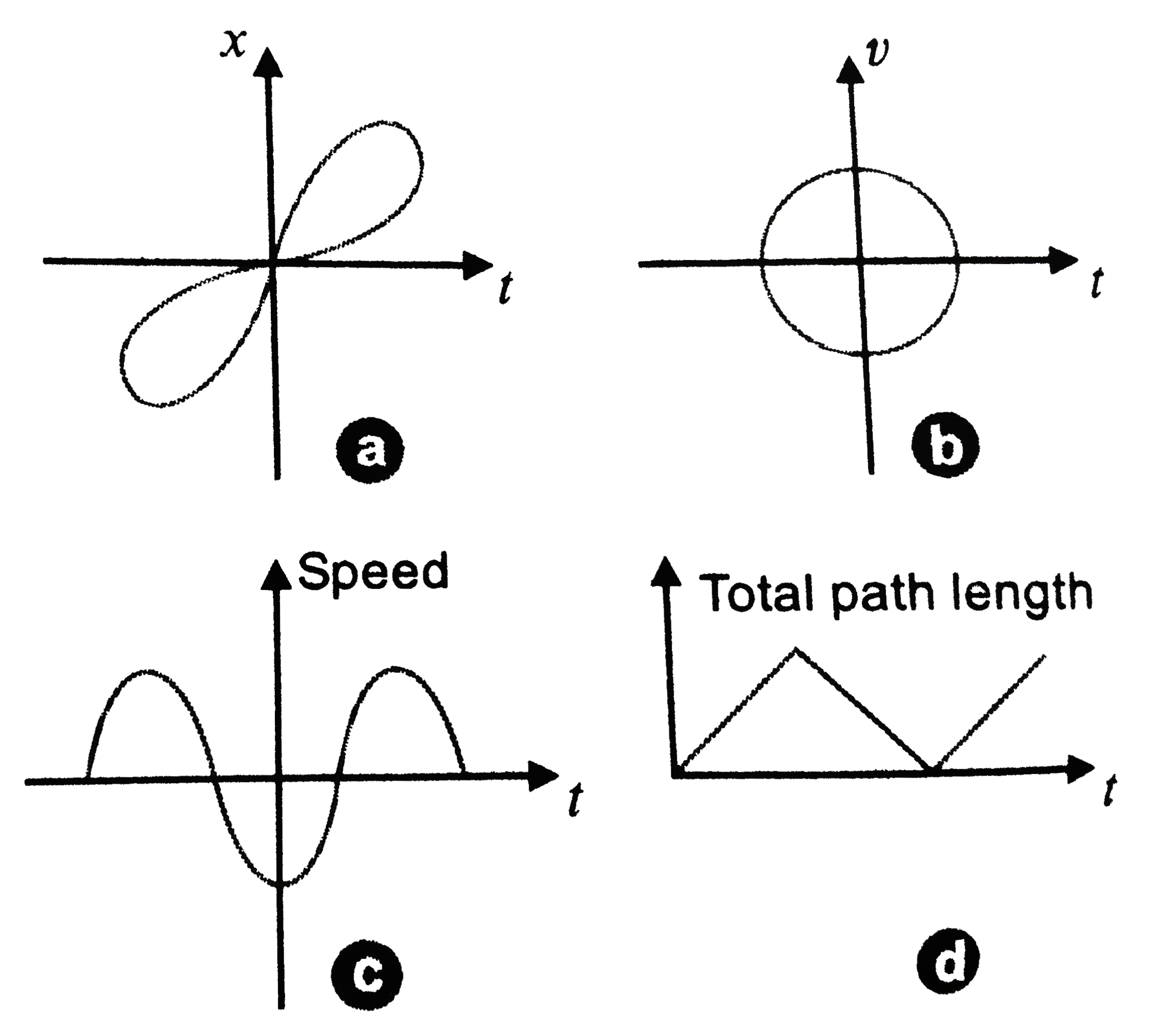
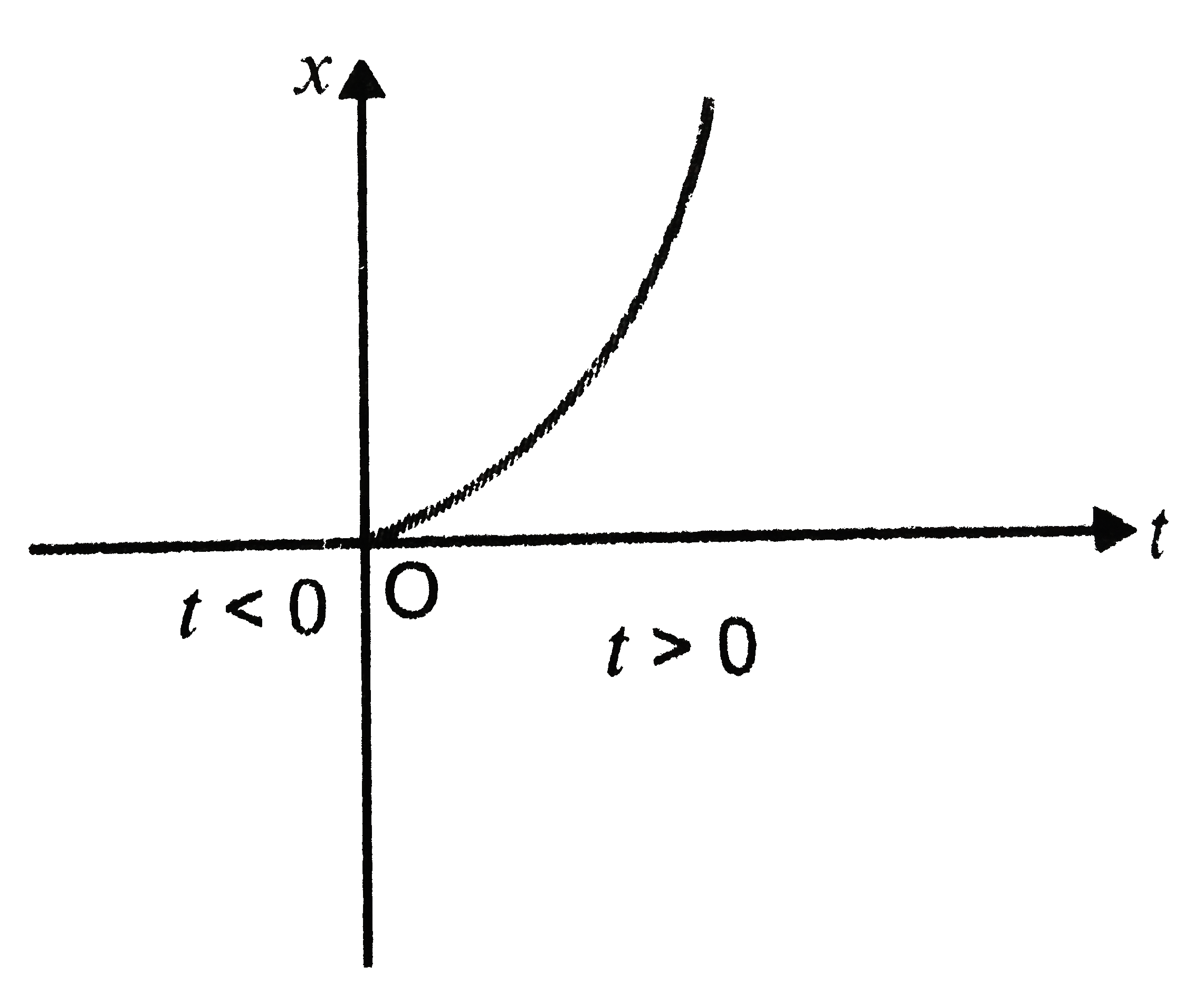
View SolutionFig. shows `x-t` plot of one dimensional motion a particle. Is it correct to say from the graph that the particle moves in a straight line for ` t lt 0` and on a parabolic path form ` t gt 0 `? If not, suggest a suitable physical context for this graph.
View SolutionA police van moving on a highway with a speed of `30 km h^(-1)` Fires a bullet at a thief's car speeding away in a same direction with a speed of `192 km h^(-1)`. If the muzzle speed of the buller is `150 m s^(-1)`, with what speed does the bullet hit thief's car? .
 .
.
View SolutionSuggest a suitable physical situation for each of the following graph . Fig.
View SolutionFig gives the `x-t` plot of a particle executing one dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particles at ` t= 0.3 s`, ` 1.2 s, - 1. 2 s`,
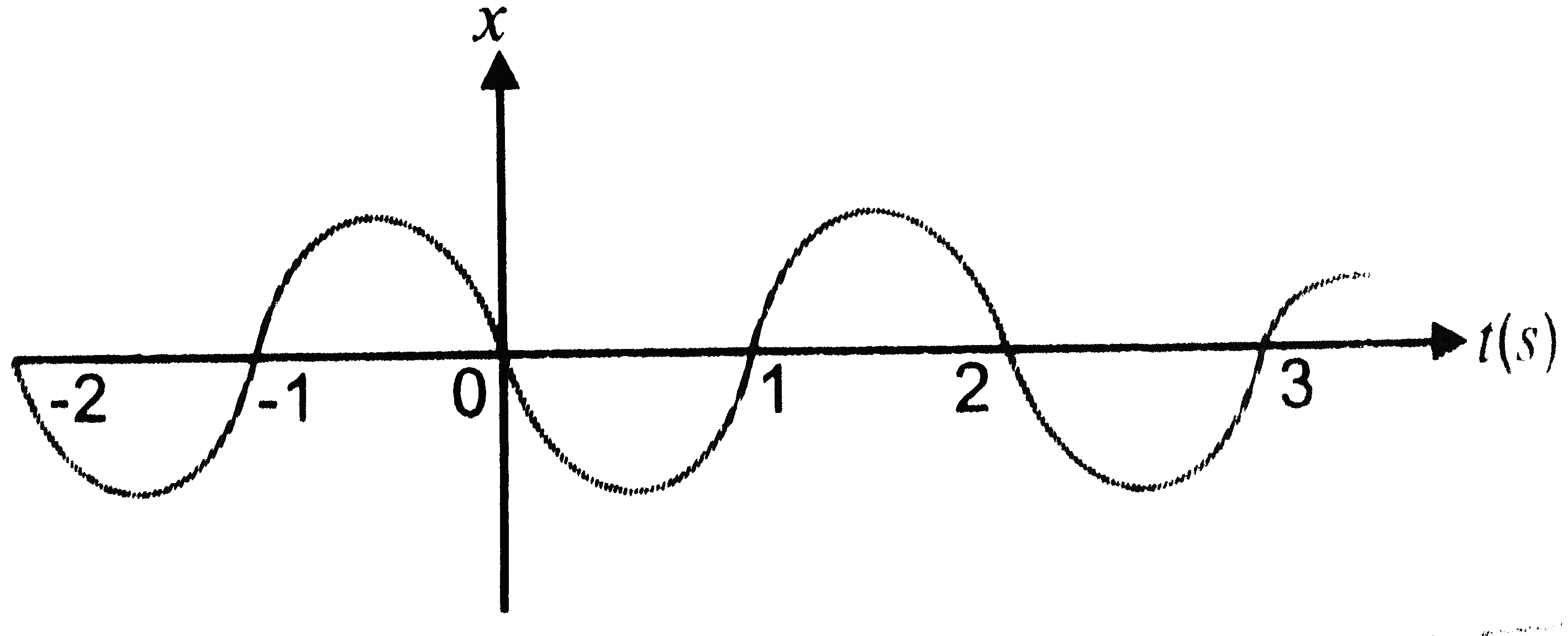
View SolutionFig. show the ` x-t` plot of a particle in one dimensional motion. Three different equal intervals of time are shown. In which interval the average speed is greatest and in which it is the least? Give the sign of average speed for each interval.
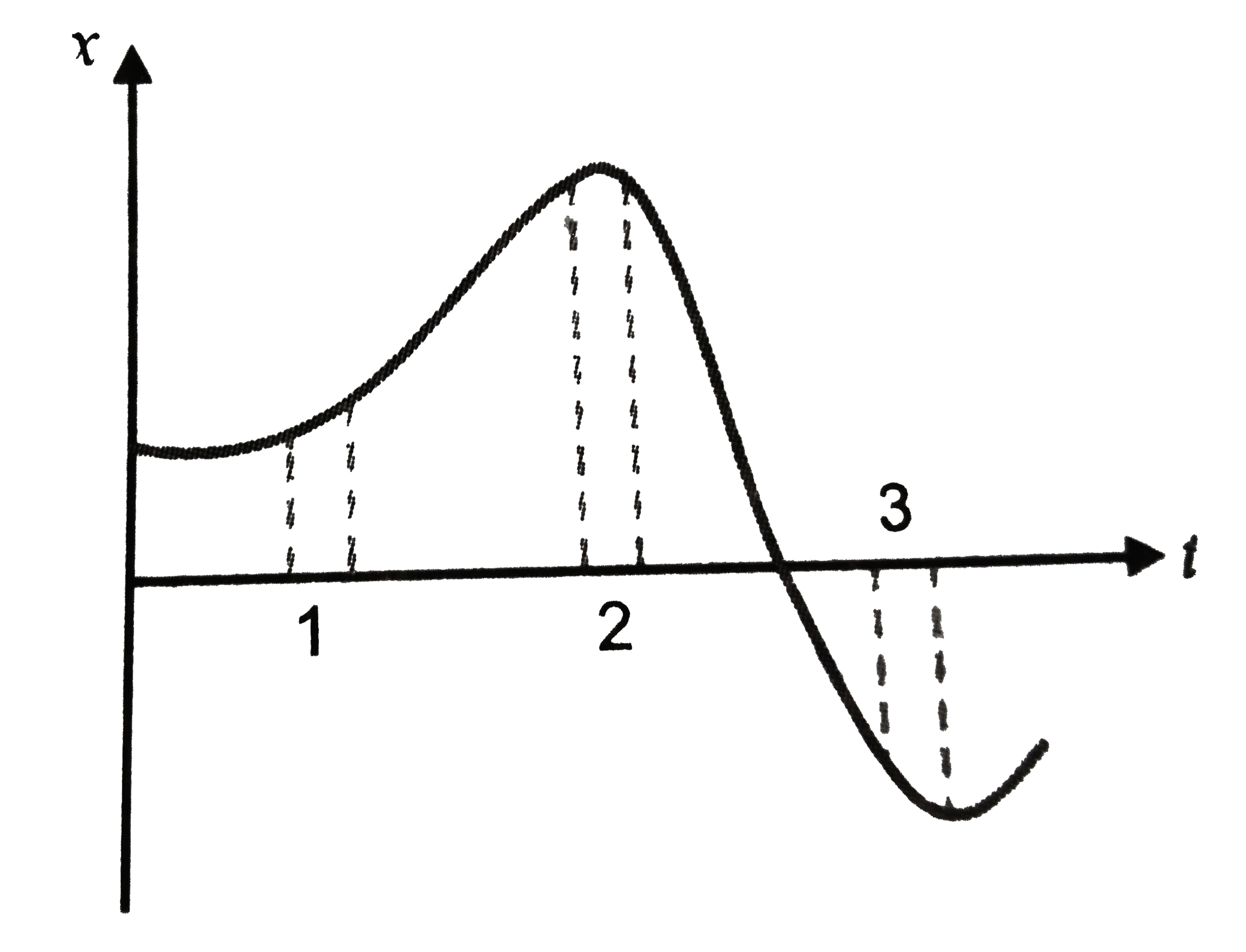 .
.
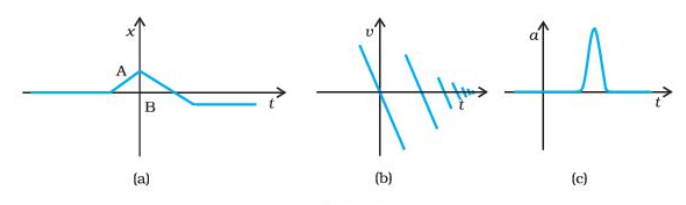
View SolutionGiven a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion, give the signs of `v` and `a` in the three intervals. What are the accelerations at the points ` A, B , C` and ` D` ?
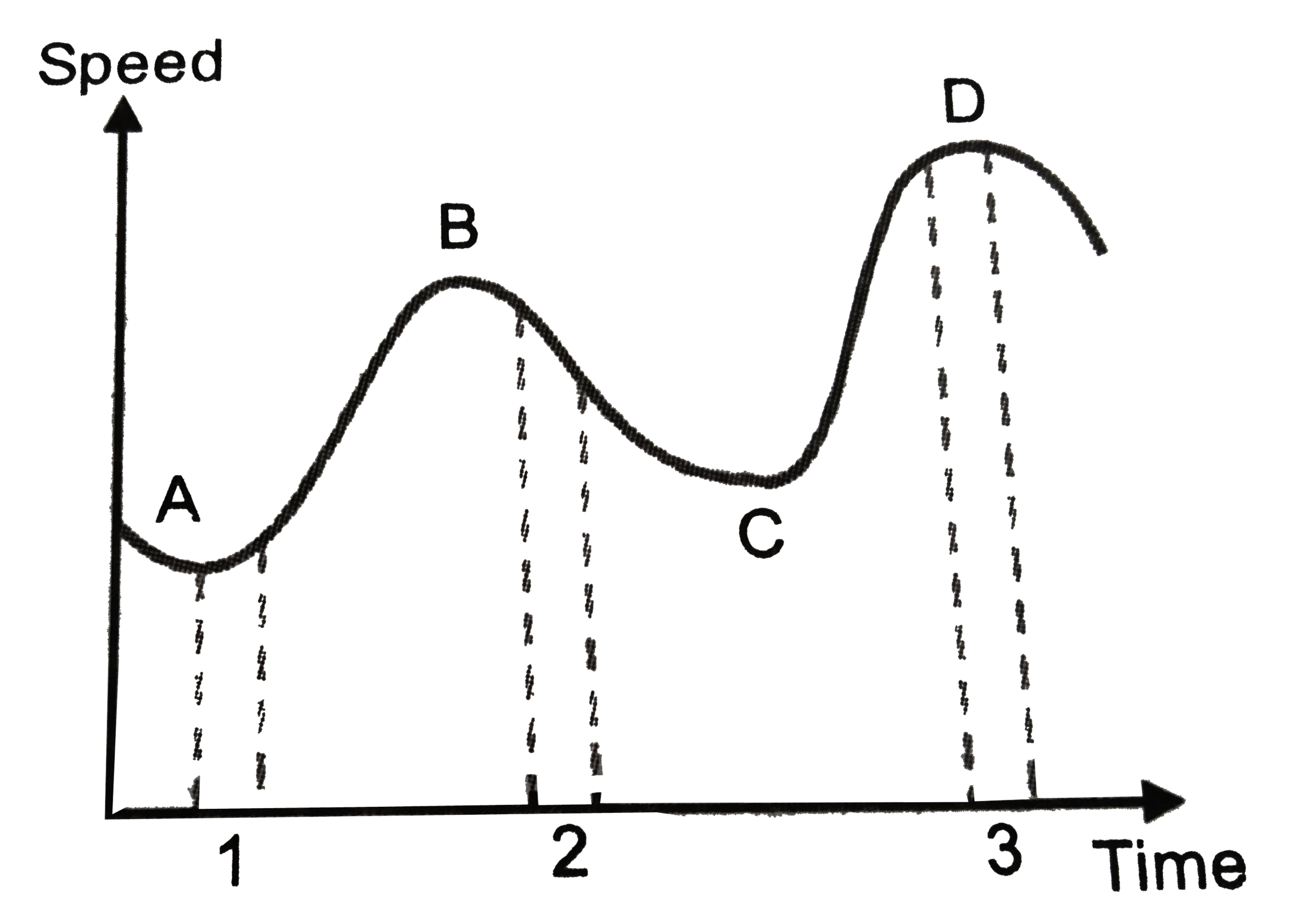 .
.
View SolutionA three wheeler starts from rest, accelerates uniformly with ` 1 ms^(-2)` on a straight road for ` 10 s` and then moves with uniform velocity. Plot a graph between the distance covered by the vehicle during the `n_(th)` second ( n = 1,2,3, ……..) versus n. What do you expect the plot to be during accelerated motion: a straight line or a parabola?
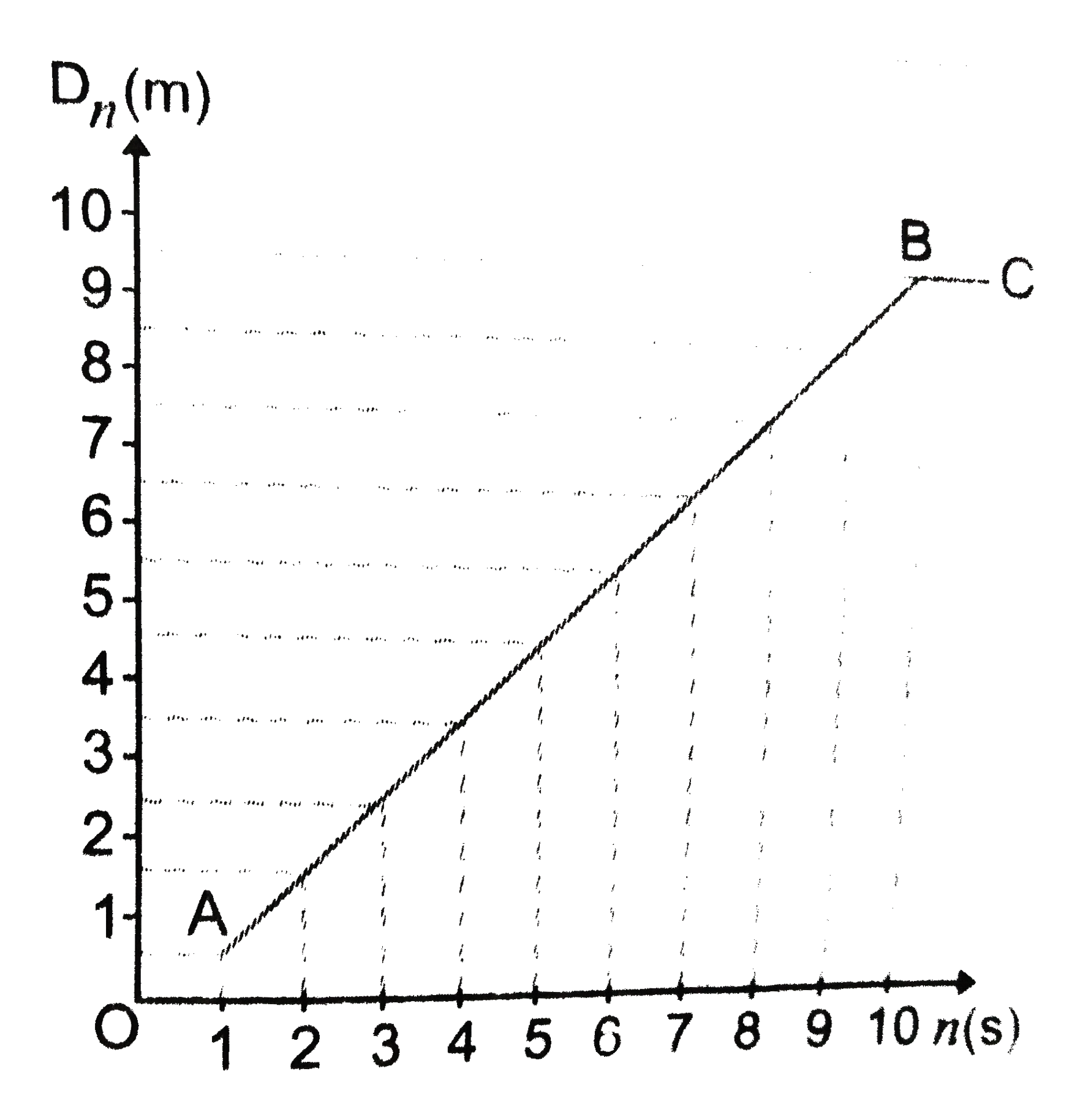 .
.
View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to ` 49 ms^(-1)`. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of `5 ms^(-1)` and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
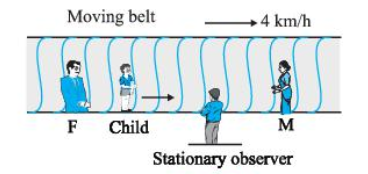
View SolutionOn a long horizontally moving belt, a child runs to and fro with a speed `9 kmh^(-1)` ( with respect to the belt) between his father and mother located 50m a part on the moving belt. The belt moves with a speed of `4 kmh^(-1)`. For an observer on a stationery platform outside, what is the
(i) speed of the child running in the direction of motion of the belt?
(ii) speed of the child running opposite to the direction of motion of the belt? (iii) time taken by child in (i) and (ii) ?
which of the answers alter if motion is viewed by one of the parents?
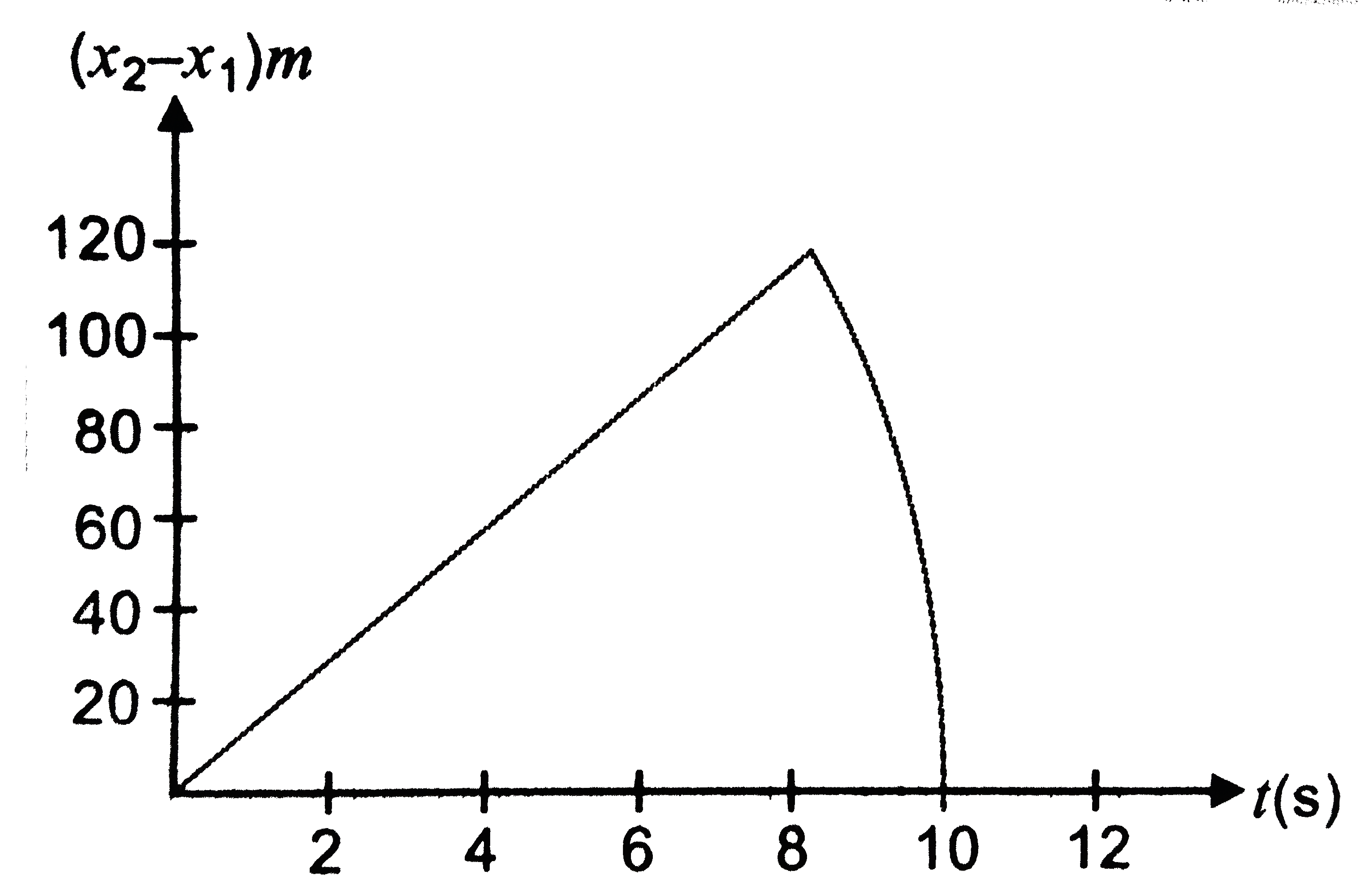
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff ` 200 m` high with initial speeds of ` 15 ms^(-1)` and ` 30 ms^(-1)`. Verify that the graph shown in Fig. 2 ( NCT). 13 , correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect the air resistance and assume that the stones do not rebound after hitting the ground. Take ` g= 10 ms^(-2)`.Give equations for the linear and curved parts of the plot.
 .
.
View SolutionThe speed-time graph of a particle moving along a fixed direction is shown in the Fig. The distance traversed by the particle between (a) `t=0 s to 10 s` .
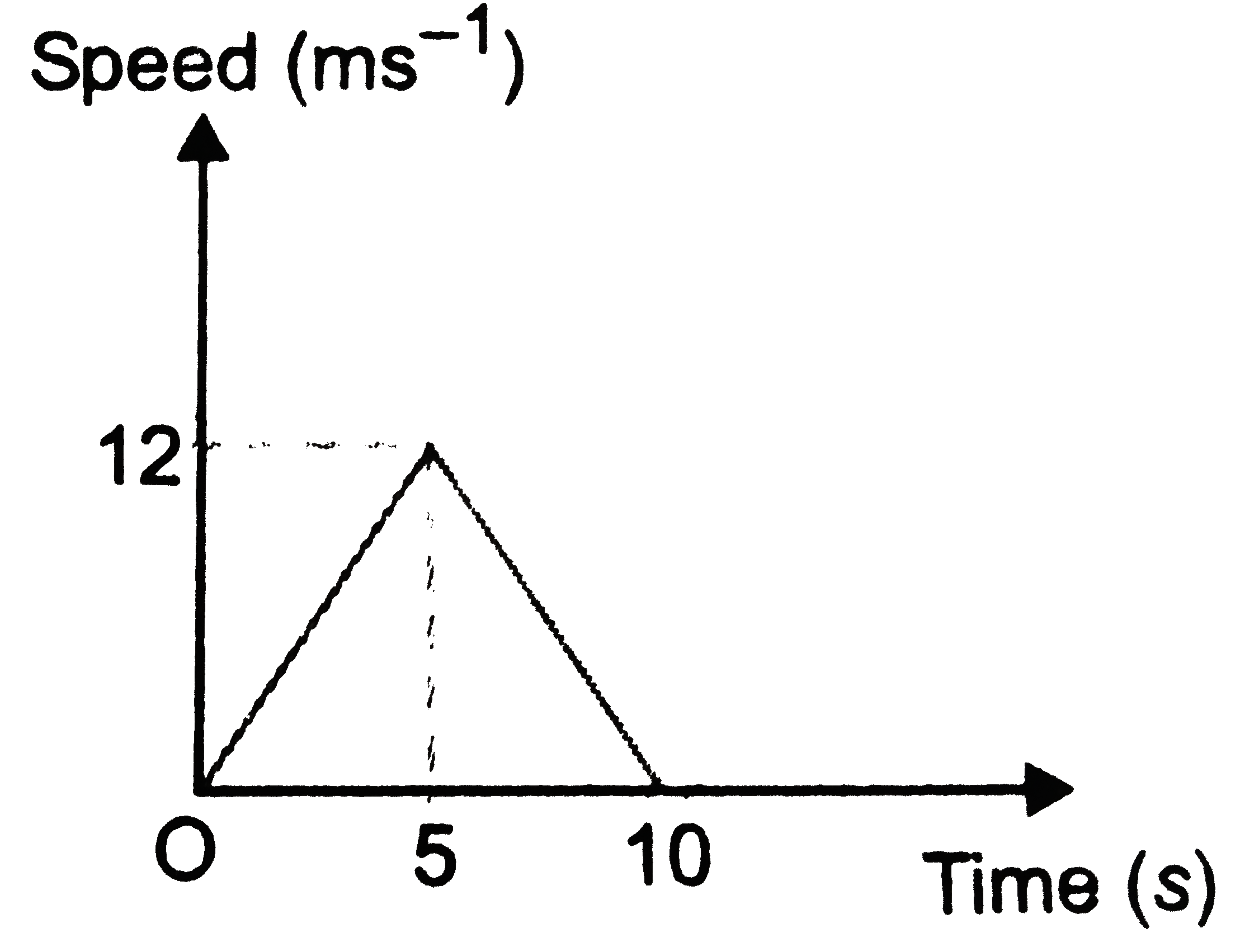 .
what is the average speed of the particle over the intervals?
.
what is the average speed of the particle over the intervals?
View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig.:

(a) Which of the following formulae are correct for describing the motion of the particle over the time-interval `t_(1)` to `t_(2)`:
(a) `x(t_(2)) = x(t_(1)) + v (t_(1)) (t_(2) - t_(1)) + (1//2) a (t_(2) - t_(1))^(2)`
(b) `v(t_(2)) = v(t_(1)) + a (t_(2) - t_(1))`
(c) `v_("average") = (x (t_(2)) - x(t_(1)))//(t_(2) - t_(1))`
(d) `a_("average") = (v(t_(2)) - v(t_(1)))//(t_(2) - t_(1))`
(e) `x(t_(2)) = x(t_(1)) + v_("average") (t_(2) - t_(1)) + (1//2) a_("average") (t_(2) - t_(1))^(2)`
(f) `x(t_(2)) - x(t_(1))` = area under the `v - t` curve bounded by the t-axis and the dotted line shown.
View Solution
EXERCISE questions and complete solutions for chapter MOTION IN A STRAIGHT LINE of NCERT PHYSICS(ENGLISH) of Class 11