Complete Solutions to Exercises (B) of chapter FRICTION, WORK POWER AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FRICTION, WORK POWER AND ENERGY |
| NN GHOSH | Exercises (B) |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
A block of mass 2kg is placed on a trolley of mass 20 kg free to move on a frictionless floor. What are the frictional force, accelerations of the block and trolley if the block is pulled by a force of 3 N ? The coefficient of friction between block and trolley is 0.25. What will be the values of all three if the block is pulled by 8 N force ? At what value of the applied force will the bodies just tend to separate ?
[Hint : So long as the force applied does not produce the limiting frictional force the two will move with common acceleration. When the force applied exceeds that limiting value the block will move on the trolley with a different acceleration]
View SolutionA block of mass `m` height `2h` and width `2b` rests on a flat car which moves horizontally with constant acceleration a as shown in figure. Determine

a. the value of the acceleration at which slipping of the block on the car starts, if the coefficient of friction is `mu`.
b. the value of the acceleration at which block topples about `A`, assuming sufficient friction to prevet slipping and
c. the shortest distance in which it can be stopped from a speed of `20 ms^(-1)` with constant deceleration so that the block is not disturbed. The following data are given `b=0.6 m, h=0.9 mu=0.5` and `g=10ms^(-2)`
View SolutionAssuming that a car whose CG is at a height `b` from the rear wheel and at a distance c from the front wheel and at a height `h` above the pavement, has sufficient power and there is sufficient friction, find the maximum acceleration that it would be able to develop without tipping over backward.
View SolutionA flexible but inextensible chain of length `l` is placed on a smooth table with an initial length `1 = nl` hanging down the table. Calcultae the velocity with which the chain will leave the table if released from rest. Consider two cases : (i) the hanging part does not touch the ground which is at a large distance, (ii) the lower end of the hanging part initially just touches the ground. Also calculate the time in which the chain leaves the table in the first case
[Hint : Taking the table as the datum and `m` as the mass per unit length of the chain, apply the principle of conservation of energy].
View SolutionCalculate of velocity `v` of the falling masss P after it has gone down by `x` in an axle and wheel system of radii r and R respectively (Figure 2.12)
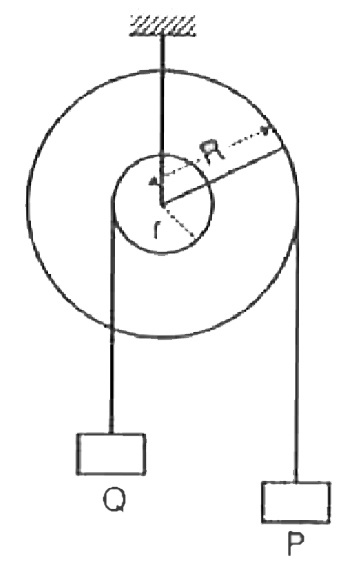
[Hint : Let Q go up by `y` when P down by x
Then `(x)/(y)=(R)/(r) :. x=(R)/(r)y`
Apply work-energy theorem to the system (P+Q+ceiling). Remember that the gravitational pulls are the lone forces external to the system, the tensions and pull of ceiling are internal forces of the system]
View SolutionIf the system if Figure 7.13 is released from rest in the configuration shown by solid lines, find the maximum distance `h` through which the weight will fall. (Neglect friction and masses of pulleys) What will happen if `P = 2Q` ?
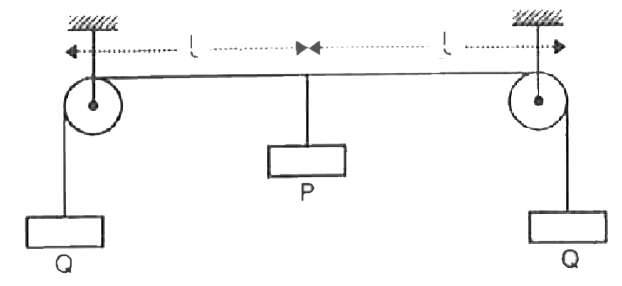
[Hint : Apply work-energy theorem to the compound system consisting of the three masses and ceiling. To find intantaneous velocities of the masses apply the condition that the length of the string remains constant. Also remember that gravitational pulls are the lone forces external to the system, the tension of the string and pull the internal force ceiling are of the system]
View SolutionA body of mass `m` starts from rest down a plane of length `l` at an angle `theta` with the horizontal. (a) find the body's speed at the bottom (b) How far will it slide horizontally on a similar surface after reaching the bottom of the incline. The coefficient of friction between the body and the plane is `mu`.
View SolutionA block A of mass 4 kg is placed on another block B of mass 5 kg , and the block B rests on a smooth horizontal table . For sliding block A on B , a horizontal force of 12 N is required to be applied on A How much maximum force can be applied on B so that both A and B move togrther ? Also find out acceleration produced by this force .
View SolutionA block A of 10 kg rests on a rouch, horizontal table and is connected to another block of mass 5 kg by a string passing over frictionless pulley. This mass hangs vertically (a) Determinem the minimum weight of a third block C which can be placed on A to prevent it from sliding if `mu_(s)=0.2` (b) The block C is suddenly lifted, then what is the acceleration of the block A ? `(mu_(k) = 0.18)`
View SolutionA block of mass `m` slides down an inclined right angled trough .If the coefficient of friction between block and the trough is `mu_(k)` acceleration of the block down the plane is

View SolutionA force of 5 N acts on a 15 kg body initially at rest. The work done by the force during the first second of motion of the body is
View SolutionThe force required to tow boat at a constant velocity is proportional to the velocity. If it takes 7460 W to two a certain boat at a speed of 4 kmph, how much horse power (1 H.P = 746 watts) will be required to tow it at a speed of 12 kmph ?
[Hint : Force `prop` velocity P = force `xx` velocity]
View SolutionWhat power is developed by a grinding machine whose wheel has a radius of 20 cm and runs at 2.5 revolutions per second when the tool to be sharpened is held against the wheel with a force of 20 kg ? The coefficient of friction between the tool and the wheel is 0.3
[Hint : Power `= Fv = F omega r = mu N omega r` where N is the normal reaction]
View SolutionConsider the system of weights `P_(1)=1 kg,P_(2) = 2 kg,P_(3) = 5kg and P_(4) = 0.5 kg` as shown in Figure 7.14. `alpha = 30^(@), g = 9.8 ms^(-2)` and the coefficient of friction between the weights and the planes is 0.2 Find (a) the acceleration of the system (b) tensions in the strings between `P_(1) and P_(2)` and that between `P_(2) and P_(2)` respectively and (c) the force with which `P_(4)` presses down on `P_(3)`
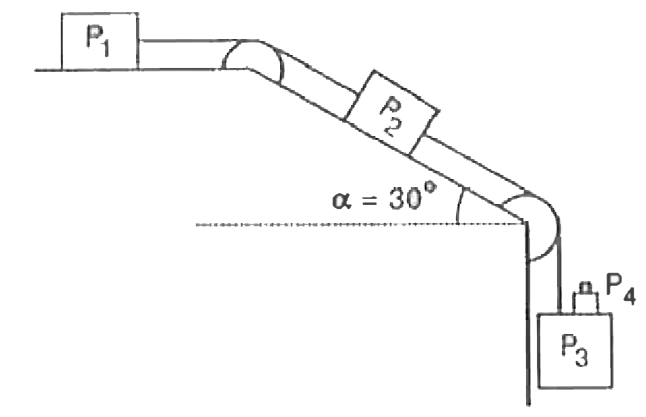
[Hint : Make free-body diagrams and apply Newton's law of motion after resolving the forces acting on a body along and perpendicular to the plane on which it lies]
View SolutionA plane surface, incline at `37^(@)` to the horizontal is accelerated horizontally till a block of mass `m` originally at rest with respect to the plane, just starts to slip up the plane. The coefficient of static friction between surfaces in contact is `mu = (5)/(9)` Find the acceleratiobn of the plane
[Hint : Applying D' Alembert's principle bring the system to rest. Make free-body diagram adn apply second law of motion]
View SolutionA weight of mass `m=1` kg attached to a spring of force constant `k = 20 N m"^(-1)` is able to oscillate on a rouch `(mu = 0.05)` steel rod. The displacement from the initial position of equilibrium is `a=30` cm. Find how many swings (i.e., movement from maximum to the equilibrium or back) will it make before coming to rest ? Take `g = 10 ms^(-2)`
[Hint : Use energy conservation to find `a_(n)` and hence have number of swings]
View Solution`M_(A) = 3 kg ,M_(B) = 4 kg ,M_(C) = 8 kg`. Coefficient of friction between any two surface is `0.25` pulley is frictionless and string is massless .A is connected to wall through a massless right rod.

View SolutionThe total mass of an elevator with a 80 kg man in it is 1000 kg. This elevator moving upward with a speed of 8 `m//sec,` is brought to rest over a distance of 16m. The tension T in the cables supporting the elevator and the force exerted on the man by the elevator floor will respectively be-
View SolutionTwo masses 1.65 kg and 3.30 kg are joined together by a massles rod parallel to an incline to `30^(@)`, over which both slide down, with the 1.65-kg mass trailing behind the 3.30-kg mass. The coefficient of friction between the first mass and the plane is 0.226 and that between the second mass and the plane is 0.113 Find (a) the tension in the rod, (b) the common acceleration of the two masses
[Hint : Make free-body diagram of the two bodies and consider their motion along and perpendicular to the plane]
View SolutionA body of mass m was slowly hauled up the hill as shown in the fig. by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force, if the height of the hill is h, the length of its base is I and the coefficient ot friction is `mu`.
 .
.
View SolutionFollowing are three equations of motion `S=ut+(1)/(2)at^(2)` `v(s)=sqrt(u^(2)+2as)` `v(t)=u+at` Where ,`S,u,t,a,v` are respectively the displacement `(` dependent variable `)`, initial `(` constant `)`, time taken `(` independent variable `)`, acceleration `(` constant `)` and final velocity `(` dependent variable `)` of the particle after time `t`. Find the velocity of the particle after 10 seconds if its acceleration is zero in interval `(`0 to 10s`)-`
View SolutionAn escalator joins one floor with another 10 m above. The escalator is 20 m long and moves along its length at `1.0 ms^(-1)`. (a) What power must its motor deliver if it is required to carry a maximum of 100 persons per minute of average mass 60 kg ? (b) If a man walks up the escalator in 10 s, how much work does the motor do on him ? (c) If this man turned around at the middle and walked down the escalatir so as to stay at the same floor, would the motor do work on him ?
[Hint : Apply work energy theorem]
View SolutionA ball of mass `m` is projected horizontally with velocity `v` into the barrel of a spring gun of mass M initially at rest on a frictionless table. The mass `m` sticks in the barrel at the point of maximum compression of the spring. What fraction of the initial energy of the ball is stored in the spring ?
[Hint : Apply energy conservation principal to the system to obtain the maximum work done on the spring which is stored as potential energy of the spring. The spring will be progressively compressed till the two acquire a common velocity]
View SolutionA block of mass 2kg slides on a frictionless table with with a speed of `10 ms^(-1)`. Directly in front of it and moving in the same direction is a block of mass 5 kg moving at `3 ms^(-1)`. A massless spring with force constant `k = 1120 Nm^(-1)` is attached to its back (the side facing 2 kg mass) When the blocks collide, what is the maximum compression of the spring ?
[Hint : Apply 'work energy' theorem to the system of block and principle of conservation of momentum]
View SolutionAn ideal massless spring is compressed by 1 m by a force of 100 N. The same spring is placed at the bottom of a frictionless inclined plane `(theta = 30^(@))`. A 10-kg mass is released from the top of the incline and is brought to rest momentarily after compressing the spring by 2m. Through what distance does the mass slide before coming to rest ?
[Hint : Apply work-energy theorem]
View SolutionMasses `M_(1),M_(2) and M_(3)` are connected by string of negligible mass which pass over massless and frictionless pulleys `P_(1) and P_(2)` as shown in figure 7.15. The masses move such that the string between `P_(1) and P_(2)` is parallel to the incline and the portion of the string between `P_(2) and M_(3)` is horizontal. The masses `M_(2) and M_(3)` are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of `37^(@)` with the horizontal. If the mass `M_(1)`moves downwards with a uniform velocity, find (i) the mass of `M_(1)`, (ii) the tension in the horizontal portion. `(g=9.8 ms^(-2) , sin 37^(@)=(3)/(5))`
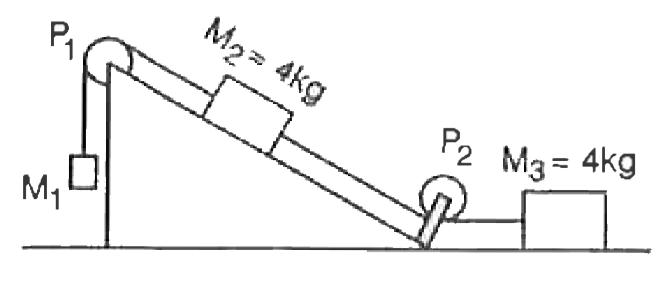
View SolutionThe handles of a table-drawer are equidistant from the sides of the drawer and are distant c from each other. Show that it will be impossible to pull the drawer out by pulling one handle if `l le mu c` where `l` is the length of the drawer from back to front and `mu` is the coefficient of friction
[Hint : Consider a force applied at inclination `theta` with the knob of the handle. Apply conditions for translational and rotational equilibrium. Hence show it is possible to draw when
`tan theta ge (l-muc)/(mu^(2)c+2mu^(2)x+2muI)`
Since `tan theta` is positive, `l ge mu c`]
View SolutionA fixed pulley carries a weightless thread with masses `m_(2) and m_(1)` at its ends `(m_(2) gt m_(1))`. There is friction between the thread and the pulley. If it is such that the thread starts slipping when the ratio of `m_(2)` to `m_(1)` is `n_(0)`. Find :
(a) the friction coefficient
(b) the acceleration of the masses when `(m_(2))/(m_(1))=n gt n_(0)`
[Hint : Consider an element of the thread of width `d theta` at angular distance `theta `from the horzontal diameter of the pulley. The forces at the ends are T and T = dT. If dN is the normal reaction of the pulley on the element than df (frictional force on the element) `= mu dN` Resolving the tensions at the ends along and perpendicular to the radius vector of the element, we have for equilibrium of the element `dT = df and dN = T d theta` Integrate from `T_(1)` to `T_(2).T_(1)=m_(1)g and T_(2)=m_(2)g`. These are obtained by considering equilibrium of `m_(1) and m_(2)`]
View SolutionA block of mass `m` is placed on the rough incline of a wedge of mass M and inclination `alpha` to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is `mu`.
View SolutionA car starts moving from rest along the circumference of a horizontal circle of radius `R =49` m with a constant tangential acceleration `a_(t)=0.62 ms^(-2)`. The coefficient of sliding friction is `mu = 0.2`. What distancem will the car describe without sliding ?
[Hint : The car will start sliding when the frictional force attains its upper bound]
View SolutionA block of mass `m=37.5 kg` is placed on a table of mass `M = 12.25 kg` which can move without friction on a levelm floor. A particle of mass `m_(0) = 0.25 kg` moving horizontally with velocity `v_(0)=302 ms^(-1)` strikes the block completely inelastically. Calculate the distance through which the block moves relative to the table before they acquire a common velocity and also calculate that common velocity (`mu` between block and table = 0.25)
View SolutionWater from the bottom of a dam of depth `h` comes out through a narrow pipe and strikes continuousy the tips of the blades of a water turbine. The length of each blade is R. Calculate the most advantaneous speed of rotation of the turbine
[Hint : The most advantageous speed corresponds to the development of maximum power in the turbine]
View SolutionA 60 kg man leaps vertically from a crouching position when his centre of mass is 40 cm above the ground. As his feet leave the floor his centre of mass is 90 cm above the ground and rises to 120 cm at the top of his leap. Calculate up upward froce, assumed constant, that the ground exerts on the man.
[Hint : Human body is a system of particles]
View SolutionWhat work should a man do to walk up a subway escalator moving down with speed `v` ? The height of the escalator is `h`, and the man walks up the escalator at a speed u.
View SolutionAn object of mass m slides down a hill of height h and of arbitrary shape and stops at the bottom because of friction. The coefficient of friction may be different for different segments of the path. Work required to return the object to its position along the same path by a tangential force is
View SolutionA skater standing on a perfectly floor holds on the nearby railing and then pushes himself away from the railing. By the time his arms are fully stretched and are about to leave the railing the gains velocity by `10 m//s`. If his armlength is 0.9 m, what is the work done by the force of the railing on him ? Is any pseudo work done by it ? Find the exerted by the railing on the skater. Assume skater's mass 70 kg.
View Solution
Exercises (B) questions and complete solutions for chapter FRICTION, WORK POWER AND ENERGY of BHARATI BHAWAN PHYSICS (HINGLISH) of Class 11