Complete Solutions to Exercises of chapter ROTATIONAL DYNAMICS, MOMENT OF INERTIA of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL DYNAMICS, MOMENT OF INERTIA |
| NN GHOSH | Exercises |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
A sphere of mass 10 kg and diameter 10 cm rolls without slipping with a velocity of 50 cm per second. Calculate its total kinetic energy.
View SolutionCalculate the moment of inertia of a cylinder of length `1.5 m`, radius `0.05m` and density `8 xx 10^(3) kg//m^(3)` about the axis of the cylinder.
View SolutionA uniform rod rotates in a horizontal plane about an axis perpendicular to its length and passing through an extreme end. Calculate the moment of inertia and kinetic energyof the rod if its length is 3m, its mass 6 kg and angular velocity 20 raidans per second.
View SolutionA sphere starting from rest rolls for 5.3s without slipping along a plane which is 1m in length. The upper end of the plane is 1 cm higher than the lower end. Find the accelerationi due to gravity.
View SolutionA couple of 10 Nm is applied to a flywheel of mass 10 kg and radius 50cm. What is the resulting acceleration? For how many seconds must the couple be applied and then removed to produce 100 rpm (revolutions per minute) in the wheel?
View SolutionIf the earth suddenly contracted to half of its present radius without losing any mass, how many hours would there be in a day? (hint: Apply the principle of conservation of angular momentum).
View SolutionA ring, a disc and a sphere all of the same radius and mass roll down an inclined plane from the same height `h`. Which of the three reaches the bottom (i) earliest (ii) latest ?
View SolutionA flywheel of mass 5 kg and radius 10 cm rolls down a plane inclined at `30^(@)` to the horizontal. It rolls from rest through 100 cm in 10s. Neglecting friction find a) the kinetic energy of the flywheel at the end of 10s, (b) the momentum of intertia of the flywheel about its axis.
View SolutionTwo point masses `m_(1)` and `m_(2)` are joined by a weightless rod of length `r`. Calculate the moment of inertia of the system about an axis passing through its centre of mass and perpendicular to the rod.
View SolutionA thin uniform rod AB of mass m and length l is hinged at one end to the level floor and stands vertically. If it s allowed to fall, with what angular velocity will it strike the floor?
View SolutionA hoop of radius 3m weighs 150 kg. It rolls along a horizontal floor so that its center of mass has a speed of `15cm//sec`. How much work has to be done to stop it? ltbrlt [Hint : A hoop is a ring]
View SolutionA sphere rolls up an inclined plane whose inclination is `30^(@)`. At the bottom of the inclined plane, the center of mass of the sphere has a translational speed of `5ms^(-1)` (a) How far does the sphere travel up the plane? (b) How long does it take to return to the bottom?
View SolutionA student sits on a stool that is free to rotate about a vertical axis. He holds out his arms horizontally, with a 4-kg weight in each hand. The stool is set in rotation with angular speed of 0.5 revolution per second. Calcualate the angular speed of the student is 90 cm and his rotational inertia is 7kg `m^(2)`.
[Hint: Use conservation principle]
View SolutionA solid sphere of 1kg reaches the bottom of an inclined plane after rolling without slipping over a horizontal plane with velocity of `20ms^(-1)`. The inclination of the plane with the horizontal is `30^(@)`. What is the velocity of the center of mass of the sphere immediately after it starts moving up the plane? Up to what distance along the plane will it rise? Assume sufficient friction to prevent slipping.
View SolutionA thin uniform rod of mass m and length l, pivoted freely at its base, is allowed to fall from a vertical position. Calcualte its angular velocity and acceleration when it has turned through `60^(@)`.
View SolutionWhat must be the relation between length and radius of a cylinder of given mass and density so that its moment of inertia about an axis through its center of mass and perpendicular to its length may be minimum?
View SolutionA circular disc is of mass M and radius r. From it a circualr piece is cut out with a radius of the disc as its diameter. Find the moment of inertia of the remainder about the axix of the disc
View SolutionA string is wrapped around a cylinder of mass M and radius r. The string is pulled vertically upward to prevent the center of mass from falling as the cylinder unwinds the string. (a) What is the tension in the string? B) How much work has been done on the cylinder once it has reached an angular speed `omega`? c) what is the length of string unwound in the time its acquires angular speed `omega`?
View SolutionA small sphere of mass m and radius r rolls without slipping on the insides of a large hemisphere of radius R whose axis of symmetry is vertical. Its starts at the top from rest. What is the kinetic energy of the small sphere at the bottom? What fraction is rotational and what transiational? What normal force does the small spheres exert on the hemisphere at the bottom?
[Hint: consider circular motion of center of mass at the bottom to calcualte normal reaction. For others consider conservation of energy.?
View SolutionA billiard ball is struck by a cue when it starts moving with velocity `v_(0)` without rolling. How far will the ball move before it ceases to slide on the table if `mu` is the coefficient of friction between ball and table?
View Solutiona) Explain why the cushion of a billard table is made to receive the impact of the billard ball at height of 0.7 d where d is the diameter of the ball.
b) With what part of a sabre should an object be slashed in order that the user does not feel the impact on the hand? Consider the sabre as a uniform lamina.
[Hint: In either case if the striking point is at such a distance that the lower point remains at rest, there will a rise no force. Such a point is called center of impact].
View SolutionA right circular cylinder of radius r and mass m is suspended by a cord that is wound around its surface. It is allowed to fall, prove that at its center of gravity will follow a vertical rectilinear path and find the accleration along this path. Determine also the tensile force in the cord.
View SolutionThe mass of the earth is increasing at the rate 1 part in `5 xx 20^(19)` per day by the accretion of meteors falling normally upon the earth's surface. Find the corresponding rate of change of the period of rotation of the earth supporting the earth to be a sphere of uniform density.
[Hint: Consider the deposit as a spherical shell and apply principle of conservation of angular momentum]
View SolutionA meter stick of length l and mass M lies on a frictionlesss table. The stick is free to move in any way on the table. A hockey ball of mass m moving perpendicuarly to the mass of the ball so that it remains at rest immediately after the collision?
[Hint: Elastic collision means that kinetic energy is conserved in the process. Consider conservation of kinetic energy, conservation of angualr momentum and linear momentum, i.e., `1/2mv^(2)` = `(1/2Mv^(2') + 1/2Iepsilon^(2)`, `mv1/2 = Iepsilon`, `mv = Mv^(')`.
Eliminate `v^(2')` and `w^(2)` from the first with the help of the other two. Use the expression `I = 1/12 MI^(2)]`
View SolutionA long light thread is wond partly around cylinder of radius r and mass m partly on a simialr cylinder but free to turn about a fixed axis. The movable one is allowed to fall from rest. Find the velocity of the cylinder as a functiono of the height h through which it has fallen. Does the cylinder fall without slipping?
View SolutionA tim,ber of mas m rests on two rollers, each of mass `m/2` and radius r and is pulled along a horizontal plane by a force P. Assuming there is no slipping and treating the rollers as right circular cylinders, find the acceleration of the timber.
View SolutionShow that in order to get a billiard ball to roll without sliding from the start the cue must hit the ball not at the center (that is, a height above the table equal to the ball's radius R) but exactly at a height `2/5`R above the center
[Hint, Consider linear momentum and angular motion of the ball. Apply the condtion for rolling without sliding. F = ma and `tau = F xx h = 2/5mR^(2)xx alpha`. Condition rolling without a sliding it a`=alphaR]`
View SolutionTwo masses 500 g and 460g are suspended from the ends of a light string passing over a frictionless heavy pulley of radius 5cm. When released from rest the heavier mass is observed to fall 75cm in 5s. What is the rotational inertia of the pulley? ltbr. [Hint: When the pulley is heavy the tensions on the two slides are different.]
View SolutionA solid cylinder of weight 20 kg and radius 7.5 cm is placed on a inclined plane with inclination `30^(@)` to the horizontal. A light thin tape is wound around the cylinder and is taken tangentially over the upper surface parallel to the plane and finally attached to a 5-kg body after passing over a light smooth pulley. Find the tension in the tape and linear acceleration of the cylinder up the plance, assuming no slip.
View SolutionA point A is located on the rim of a wheel of radius R which rolls witout slipping along a horizontal surface witih velocity V. Find the total distance traversed by the point A between successive moments at which it touches the surface.
View SolutionA plank of mass `m_(1)` with a sphere of mass `m_(2)` on it rests on a smooth horizontal surface. A canstant horizontal force F is applied to the plank. With what sliding between the plank and the sphere?
[hint: Rel vel. Of the lowest point `v-(2) + epsilonR -v_(1)`=0 for no sliding)
View SolutionIf in the loop-the-loop track of figure a small spherical ball of mass m is released and it rolls without slipping down the loop, calcualte the normal force exerted by the track on the ball when it is at the highest position. Take R: r=`6:1`
View SolutionA uniform rod of length 2a is held at inclination `alpha` with the horizontla with its lower end at a height h above a horizontal plane surface and is let fall. It rebounds elastically from the plane. If you just before the other end touches the plane the rod makes the same angle with the horizontal, find the value of h in terms of a and `alpha`.
View SolutionAn experimentor stands on a stool capable of rotating about a vertical axis and holds a rotating wheel of moment of intertia `I_(1)` about its axis and angualr velocity `epsilon_(1)` with its axis coinciding with the vertical axis of the stool. The moment of inertia of the stool and the experiment about the vertical axis is `I_(2)`. Calculate the change in kinetic energy of the system if the experiment rotates the wheel through
i) `180^(@)` and ii) `90^(@)`
View SolutionA uniform cylinder of radius R, and mass M rotates freely about a stationary horizontal axix O. A thin cord of length l and mass m is wound on the cylinder in a single layer and its free end is falling vertically. Find the acceleration as a function of the length x of the hanging part of the cord. Assume the center of mass of the wound part of the cord to be the axis of the cylinder.
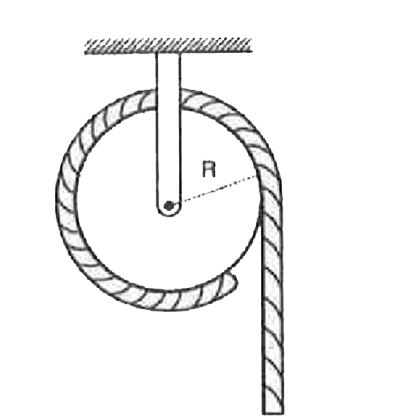
View SolutionA carpet of mass `M` is rolled along its length so as to from a cylinder of radius `R` and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to `R//2`.
View SolutionA man of mass m stands on the edge of a horizontal unifom disc of mass M and radius R whichis capable of rotating freely about a stationary vertical axis passing through its center. At a certain moment the man starts moving along the edge of the disc, he shifts over angle `theta` relative to the disc and then stops. Find the angle through which the disc rotates.
View SolutionA uniform solid cylinder of radius R=20cm rolls over a horizontal plane and passes on to an inclined plane meeting the horizontal plane at angle `alpha=30^(@)` with the horizontal. Find the maximum value of velocity `v_(0)` which still permits the cylinder to roll into the inclined plane without a jump. Assume sliding to be absent.
View SolutionA particle at angular position `theta_(0)` inside a fixed smooth hemispherical bowl of radius r is projected horizontally with velocity `v_(0)`. Calculate its value so that the particle may rise to the top.
View SolutionTwo cylinders with radii `r_(1)` and `r_(2)` and rotational inertia `I_(1)` and `I_(2)` are supported on their horizontal axles. The first one is set in rotation with angular velocity `epsilon`. The axle of the other cylinder (smaller) is moved until it touches the large cylinder and is caused to rotate by the frictional forces between the two. Find the angualr velocity of the two cylinders after slipping ceases between them.
[Hint: Consider angular impulse received by the cylinders]
View SolutionCalculate the vertical and horizontal reactions of the pivot when the rod of the problem 15 has turned through `theta=60^(@)`.
View SolutionA small body A is fixed to the inside of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane, at the moments when the body A gets into the lower position, the centre of the hoop moves with velocity `v_0`(figure). At what values of `v_0` will the hoop move without bouncing?

View Solution
Exercises questions and complete solutions for chapter ROTATIONAL DYNAMICS, MOMENT OF INERTIA of BHARATI BHAWAN PHYSICS (HINGLISH) of Class 11