Complete Solutions to EXERCISES of chapter HYDROSTATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | HYDROSTATICS |
| NN GHOSH | EXERCISES |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
A raectangular tank 2 m deep, 5 m broad and 10 m long is filied with water . Calculate the thrust on each of the sides and on the base . Density of water `1000 kg m^(-2) and g=9.8ms^(-2)`)
View Solutionif the atmosperic presssure is `1.1 xx 10^(5)Nm6(-2)` (pascal ) and the diameter of Magderburg hemispheres are 40 cm find the force required to pull them asunder.
View SolutionA cube floating on mercry has 1/4 of its volume will remain immresed in mercury? (Relative density of mercury =13.6)
View SolutionA block of wood weight 4 kg and has a relative density 0.6 . It is to be loabed with lead so that it will folat completely immersed. What weight of lead is needed (a) if the lead is on top of the block (b) if the lead is attached below the block ? Density of lead=`11.34xx10^(3) kg m6(-3)`
View SolutionA metal plate measuing 2m x 1m is immersed in water and is held there with is shorter side parallel to the free surface at a depth of 5 meters. Calculate the thrust on the plate , (i) when it is horizontal (ii) when it is vertical ,(iii) when it is at an inclination of `30^(@)` with the vertical .
View SolutionA sperical iron shell floats almost, completely submerged submerged in water . If its outer diameter is 0.5 m and the relative density of iron is 8 m find the inner diameter.
View SolutionA cylinder of iron floats vertically and fully immersed in a vessel containing mercury and water. Find the ratio of the length of the cylinder immersed in water to that immersed in mercury. (Relative density of mercury = 13.6 and that of iron = 7.78)
View Solutionthe stem of a common hydrometer is divided into 100 equal parts. It reads 0 in water and 100 ina liquid of relative density 0.8. find the relative density of the liquid in which it reads 50 .
View Solutionthe stem of a hydrometer is diveided into 100 equal parts. It reads 0 in water and 100 in a liquid of reative density 0.8 . Find the realtive denstiy of the liquid in which it reads 50.
View SolutionA U-tube contains water in its lower part. Then 32 cm of kerosene of relative density 0.8 is poured into one limb and a vegetable oil of reative density 0.65 is poured into the other. The water level in the kerosene oil side is 5 cm lower that in the other . what is the height of the column of vegtable oil ?\
View Solutiontwo bodies counterpoise each other when suspended in water from the arms of a balance. The mass of one body is 0.28 kg and its relative density 5.6 . It the mass of the other is 0.36 kg, what is the realtive density of the other body ?
View SolutionA U-tube contains water in its lower part. Then 32 cm of kerosene of relative density 0.8 is poured into one limb and a vegetable oil of reative density 0.65 is poured into the other. The water level in the kerosene oil side is 5 cm lower that in the other . what is the height of the column of vegtable oil ?\
View Solutiontwo bodies counterpoise each other when suspended in water from the arms of a balance. The mass of one body is 0.28 kg and its relative density 5.6 . It the mass of the other is 0.36 kg, what is the realtive density of the other body ?
View SolutionCalculate the depth of water at which a bubble of air would just float. Density of water `=1000 kg^(-3)` and density of air `= 1.29 kg ^(-3)`. Atmospheric pressure =`10^(5)` pa.
View SolutionA tube 1.5 m long and closed at on end is half filled with mercry and is then inverted with its open ends just dipping into a mercury tough.Find the height of mercury in the tube if the reading of the barometer is 0.75 m.
View Solutiontwo cylinders A and B are of the same dimensions but of different materials. A alone flots in a liquid with half of its length immersed. When B is placed over A , the combination just floats in the same liquid . Compare the densities of the two cylinders A and B.
View SolutionA tube 2m long and closed at on e end is half filled with mercury and is then inverted with its open end just dipping into a mercury trogy. Find the height of mercury which will stand in the tube if the reading of the barometer is o.75 m.
[hint: `P_(1) = 0.765,V_(1)= 1 propm^(3), P_(2)=(3//4-x),V_(2)= (2-x)prop m^(3),use p_(1)V_(2)=P_(2)V_(2).]`
View SolutionA column of mercury of 10cm length is contained in the middle of a narrow horizontal 1m long tube which is closed at both the ends. Both the halves of the tube contain air at a pressure of 76 cm of mercury. By what distance will the column of mercury be displaced if the tube is held vertically?
View SolutionThe volume of an air bubble becomes 8 times the original volume in rising from the bottom of a lake to its surface. If the barometice height is 0.76 m of mercury (density of mercury is `13.6 g cm^(-3) and g = 9.8 ms^(-2))` what is the depth of the lake ?
View SolutionA bottle whose volume is `0.45 xx 10^(-3) m^(3)` is sunk mouth downwards below the surface of water in a tank. How far must it be sunk so that `0.75 xx 10^(-4) m^(3)` of water may run up into bottle ? The atmospheric pressure `=10^(5) Nm^(-2)` and density of water `=1000 kg m^(-3)`
View SolutionThe volume of an air bubble becomes 8 times the original volume in rising from the bottom of a lake to its surface. If the barometice height is 0.76 m of mercury (density of mercury is `13.6 g cm^(-3) and g = 9.8 ms^(-2))` what is the depth of the lake ?
View SolutionA fauly barometer reads 71.12cm and 76.20cm when a true barometer reads 72.39cm and 78.74cm, respectively. Find the ture reading when the faulty barometer stands at 73.66cm.
View SolutionThe hieght of a mercury barometer is 75.6 cm . the baromter tube has cross -section of `1cm ^(2)` and the volume of the enclosed space above the mercury surface is 10 cc. one cc of air at atmospheric pressure is introduced into the tube. Find the change in the reading of the barometer.
View Solutionthe height of a mercury barometer is 76 cm at sea level and 50 cm at the top of a hill. Determine the height of the hill. (Densities of air and mercury are `1.36 kg m^(-3) and 13.6 xx 10^(3) kg m^(-3))`
hint : Difference of pressure =76 cm - 50 cm = 26 cm of mercury
` 0.26 xx 9.8 xx 13.6 xx 10^(3) Nm^(-2)`
pressure due to h metre of air = `h xx 9.8 xx 1.36`]
View Solutionthe height of mercury in a fauilty barometer is 75 cm and the tube above mercury is 10 cm long. The correct barometer reading is 76 cm. when the faulty barometer reads 74 cm, find the true barometer reading .
View SolutionThe neck and bottom of a bottle are 2 cm and 20 cm in diameter respectively if the cork is pressed with a force of 1.2 kgf in the neck of the bottle, calculate the force exerted on the bottom of the bottle.
View Solutionin a Bramha's press the area of the two plungers are `2cm^(2) and 60 cm^(2)` respectively. The pump plunger is worked by a lever whose arms are 5 cm and 75 cm. if the end of the lever is raised and lowered by 30 cm at evergy stoke, find the numberof strokes required to raise the press plunger by 2cm .
View SolutionA pump in the basement of a garage is used to poerate a hyfraulin hack on the firest floor. The areas of the of the two piston is 3 m higher than the other one . How great a load can be lifted by a force of 10 kg applied to the lower piston ?
View Solutionthe presseure inside th receiver of an air pump is reduced to 1/4 of the initial pressure after 3 strokes. What will be the pressure after 8 strokes ?
View Solutionin an air pump, the volume of the barral is 1/10 that of the receiver. If in the the volume of the vessel. Calculate the density of air in the vessel after 15 complete strokes.
View Solutionthe cylinder of a water pump is 4 cm above the surface of water in a well. If the readius of the cylinder of the pump be 5cm, calculate th e force acting on the piston while the pump is working.(Density of water `= 1000 kg m^(-3)`)
[ hint : force = area x pressure due to 4-m high column of water .]
View Solutionthe barral of a common pump (pump for warer ) is 50 cm long and its bottom is 6 m from the surface of water. If the cross - section of the cross - section of the thinner pipe joining the barrel with water in well 3/14 of that of the barrel, find the height of the water in the pipe after the first stoke. (water barometer is 9 m of water .
`A xx 1/2 + 3/14Axx (6-x)
A(24/14 - 3/14x)A/14(25-3x)`
final pressure =(9-x)m of water , now use `P_(1) V_(1) = P_(2) V_(2)`]
View SolutionA vessel is filled with mercury to a hiegt of 0.9 m . Could the vessul be completely empited with the aid of a siphon ? If not , to what extent can it be empited ? (Barometer reading is 0.7 m mercury)
View SolutionA canal lock gate is 4 m broad and the depth of water on opposite side of the gate are 5m and 2m . Find the resultant thrust on the gate and the torque tending to ture the gate about its base. Density of water `= 1000 kg m^(-3) and g = 9.8 m s^(-2)`
View Solutionto what height must a cylinder must a cylinder be filled with a liquid so that the thrust on the side may be equal to the thurst at the bottom ?
View SolutionTwo identical cylindrical vessel with their bases at the same level each contain a liquid of density `rho`. The height of the liquid in one vessel is `h_(1)` and in the other is `h_(2)` the area of either base is A. What is the work done by gravity is equalising the levels when the two vessels are connected?
View SolutionA iron shell loses half its weight in water. What portion of its volume is hollow ? ( Relative density of iron =7.5)
View SolutionA cylinder of relative density 0.7 is 0.5 m high and the radius of its base is 1m . It floats in water with its axis vertical . Find the legth of the cylinder inside water. What force is needed to raise it by 1 cm ? Denstiny of water =1000 kg `m^(-3)`
View SolutionA ship with cargo sinks by x when she goes into a river from the sea. She discharges cargo and proceding again to sea, she rises by z. if the sides of the ship be assumed to be vertical to the water, show that relative density of sea water is `y/(z-x+y)` , assuming relative density of river water to be 1 .
View SolutionA beaker containing water (weighing 150 g) is placed on the pan of a balance which shows a reading of 200g on the other pan (a) now the stone is put into the beaker. Will they weigth the same, more or less ? (b) It the ston eis suspended b a thread from an extenal support and allowed to sink into water without touching any part of the beaker, what weight will be required balance ? (Density of stone =2000`kg m^(3)`)
View SolutionA beaker containing water is placed on the pan of a balance which shows a reading of 200 g. A lump of sugar weighing 75 g and of volume 30 cc is now suspended inside the water from an external support without touching any part of the beaker. (a) what will be the reading just when the lump of sugar is immersed ? how will the reading change as time passes ? (b) what will be the initial reading if the lump is simply dropped gently into the beaker and how will the reading change?
View SolutionA boat flaoting in a water tank is carrying a number of large stones. If the stones are unloaded into the water, what will happen to the water level in the tank
[ hint : Assume the initial level of the tank to be K and the length of the boat immersed in water to be h. Apply the law of floatition. find the volume of water in th tank. repeat the process after a plece of stone is unloaded. the stone will sink to the bottom .
assume the new height to be H' and h' respectively.
make use of the fact that the volume of water remains constant .
`H-H=V/A((P_(s))/(P_(w))-1)`
where V = volume of stone , A = area of cross - section of tank , `P_(s)` = density of stone and `P_(w)` = desnsity of water .]
View SolutionA breaker filled with water up to the brim contanis a piece of ice floating in the water . Will water spill as ,ice melts ?
[ Hint : In th eprocess, total mass (mass of ice + mass of water ) remains constant, show that `H=(M=m)/(A_(Pw))` wher M is the mass if water, m=mass if teh ice, A= area of cross - section of the veaker and `P_(w)` = desnity of water .]
View SolutionA man ina boat drink water from alake. Will the level of water of the lake fall or rise ?
View SolutionA man is a boat scoops out a stone from the bottom o f a lake and puts it in his boat. Will the level of water is the lake rise or fall ?
View SolutionIn problem 43 if the piece of ice contains a piece of brass, will the water spill out ?
View SolutionIN problem 43 , what difference will be observed (a) if the water is hot ,(b) if the water is at `4^(@)C` ?
View SolutionIn problem 43 , if the piece of ice contains a piece of cork . Will water spill out ?
View SolutionAn ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals `76cm` of mercury. The lenghts of the mercury column and the trapped air column are `20cm` and `43cm` respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of `60^(@)`? Assume the temperature to remain constant.
View SolutionA vertical cylinder of total lwgth 100 cm is closed at the lower end and fitted with a movable , frictionless, gas - tight disc ,at the other end. An ideal gas is trapped under the disc of negligible mass. Initially the height of the gas column is 90 cm and the dis is in equlibrium . Mercury is slowly poured on the top of the disc and it just starts overflowing when the disc has descended thorugh 32 cm. find the atmospheric pressure.
View SolutionTwo spheres of volume 250 cc each but of relative densities 0.8 an d 1.2 are connected by a string and the combination is immersed in a liquid. Find the tension T in the string. `(g=10m//s^(2))`
View SolutionTwo non - viscous, incompressible and immiscible liquids of densities (rho) and (1.5 rho) are poured into the two limbs of a circular tube of radius ( R) and small cross section kept fixed in a vertical plane as shown in fig. Each liquid occupies one fourth the cirumference of the tube.
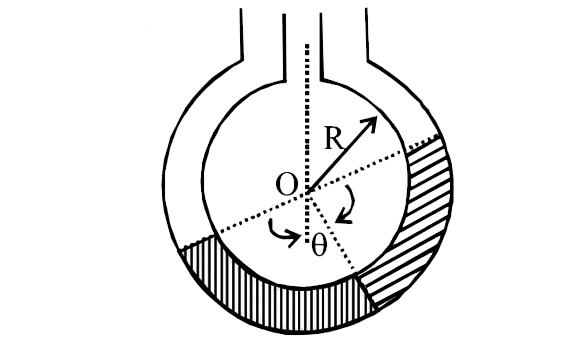 .
.
(a) Find the angle (theta) that the radius to the interface makes with the verticles in equilibrium position.
(b) If the whole is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the period of these oscillations.
View SolutionA common hydrometer has a small portion of its bulb rubbed off due to fequent use. In consquence when placed in wter it appears to indicate the sp . Gravity of water 1.002 find the fraction fo its weight lost dure to frquent use .
View Solutionfind the density of air at any height and hence the height at which it is halved. Assume that the temperature reamins fixed throughout the atmosphere. The pressure at the earth's surface is `P_(0) = 1.012 xx 10^(5) Nm^(-2)` and density ` p_(o)=1.293 kg m^(-3)`
View Solutionan oil tanker moving with speed `v` decelerates uniformly and comes to a stop within a distance s . Find the pressure due to the oil to the back and front walll of the tanker during the period of deceleration. Assume the taker to be a parallelpiped of length l, width b and heigth lt and the density of the oil to be p.
View Solutionthe base of cylindrical vessel is hemesphericl in shape with rdius R . If the vessel is filled with liquid of density p up to a height h. calculate the thrust on the base.
View SolutionA lipuid is poured into a cylindrical vessel of height H and mass M. to what height a liquid of density p should be poured so that the centre of gravity of the vessel + kuqyud ' sustem mat be at the minimum height from the bottom . Negalect the mass of the bottom .the area of cross - section of the vessel of A .
View SolutionA container contains a liquid whose density varies from free surface ar p =ax+ b where `a=4xx10^(3) kgm^(-4) and b= =10^(-3)` cylindrical solid of length l=0.75 m and denssity `sigma=0.5xx10^(3) kgm^(-3)` is floated in the liquid. Calculate the length of the cylinder inside the liquid .
View SolutionA long metal rod of length I and density p is held vertically with its lower end touching sea-water of density `p_(0)`. Calculate the time in which the whole of the rod will sink into water and the velocity of the rod. Negtect water resistance and assume vertical postion of the rod throughout its motion .
View Solution
EXERCISES questions and complete solutions for chapter HYDROSTATICS of BHARATI BHAWAN PHYSICS (HINGLISH) of Class 11