Complete Solutions to Illustravtive Example of chapter NEWTONS LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION |
| PHYSICS GALAXY | Illustravtive Example |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
Find the acceleration of masses `m_(1)` and `m_(2)` connected by an inextensible string, shown in figure-2.13(a). The string and pulley are assumed to be massless and frictionless.
View SolutionA situation is shown in figure-2.15, Find the acceleration of masses `m_(1)` abd `m_(2)` mass of pulley is `m_(P)`. Consider the string going over the pulley is massless and frictionless.

View SolutionFind the acceleration of masses `m_(1)` and `m_(2)` moving down the smooth incline plane. The string and the pulley are masseless and frictionless.
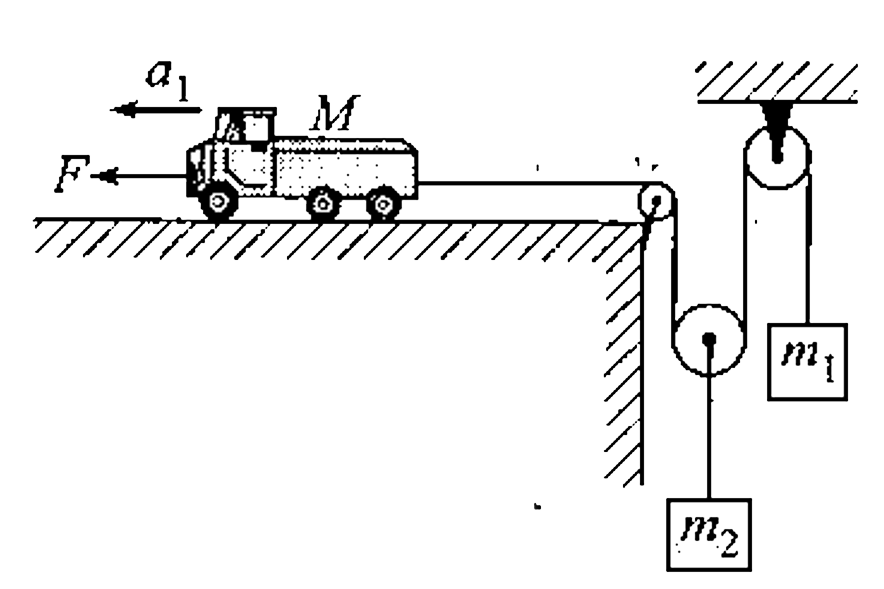
View SolutionA toy truck of mass M is moving towards left with an acceleration `a_(1)` as shown in figure-2.17. It is connected to a mass `m_(1)` with a massless and frictionless string, going over a movable massless pulley, to which another mass `m_(2)` is connected. Find the force acting on the truck towards right and the acceleration of masses `m_(1)` and `m_(2)`
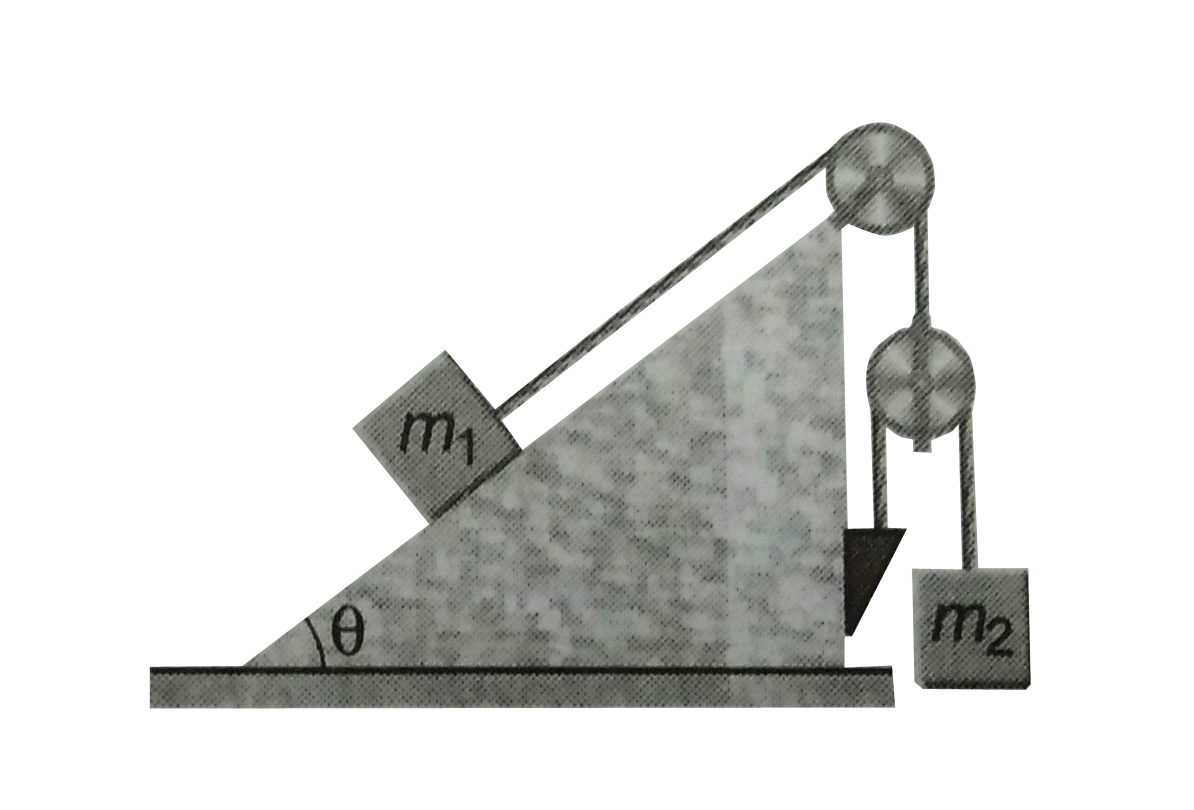
View SolutionFind the acceleration of the body of mass `m_(2)` in the arrangement shown in figure. If the mass`m_(2)` is `eta` time great as the mass `m_(1)` and the angle that the inclined plane forms with the horizontal is equal to `theta`. The masses of the pulley and threads, as well as the friction, are assumed to be negligible.
View SolutionIn the arrangement shown in figure the mass of the ball is `eta` times as that of the rod. The length of the rod is `L` the masses of the pulleys and the threads as well as the friction, are negligible. The ball is set on the same level as the lower end of the rod and then released. How soon will the ball be opposite the upper and of the rod?

View SolutionThe object in fig. weighs 40kg and hangs at rest. Find the tensions in the three cords that hold it.

View SolutionA cubical block is experiencing three forces `F_(1) = 20 N` acts at angle `45^(@)`with horizontal and lies in diagram plane of the cube `F_(2) = 30 N` acts along y- axis and `F_(3) = 40 N` acts in x- direction as shown in fig find the friction force acting on the block if it is at rest

View SolutionA chain of mass 'm' is attached at two points `A` and `B` of two fixed walls as shown in the Find the tension in the chain near the walls at point `A` and at the mid point `C`
 .
.
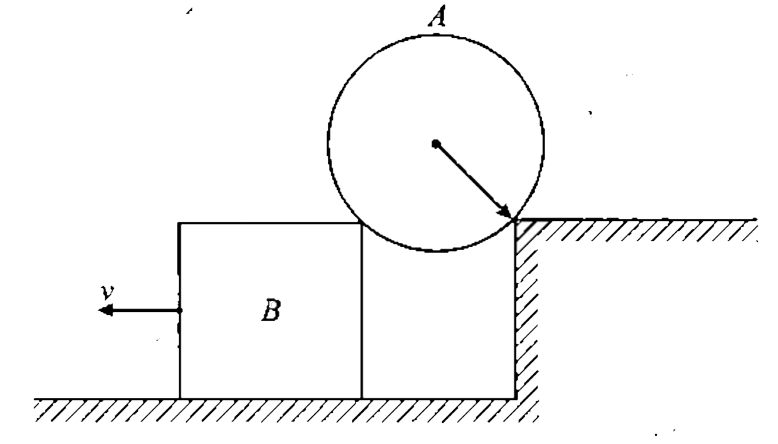
View SolutionFigure-2.35 shows a cylinder A of mass M which is resting on two smooth edges, one fixed and other is that of a block of B. At an instant block B is pulled toward left with a constant speed v. Find the force exerted by the cylinder on the fixed edge after some time when the distance between the two edges will become `x = sqrt(2)R. "At " t = 0` the distance betwween the two edges was zero.
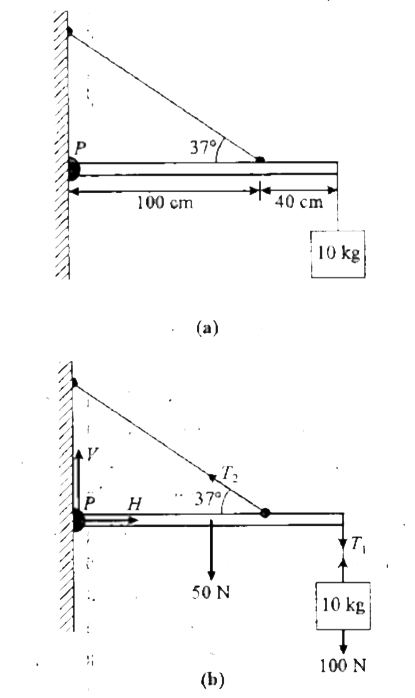
View SolutionIn figure-2.40(a), we see a beam of length L pivoted at one end and supporting a 200 kg object at the other end. Find the tension T in the supporting cable that runs upward to the ceiling. Assume that the weight of the negligible. Take `g = 10m//s^(2)`
View SolutionFor the uniform 5 kg beam shown in figure-2.41(a), how large is the tension in the supporting cable and what are the components of the force exerted by the hinge on the beam ? Take `g = 10 m//s^(2)`
View SolutionThe uniform 20 kg ladder hinged at the bottom in figure-2.42(a), leans against a smooth wall. If a 40 kg person stands on the ladder shown, how large are the forces at the wall the ground Take ` g = 10 m//s^(2)`.
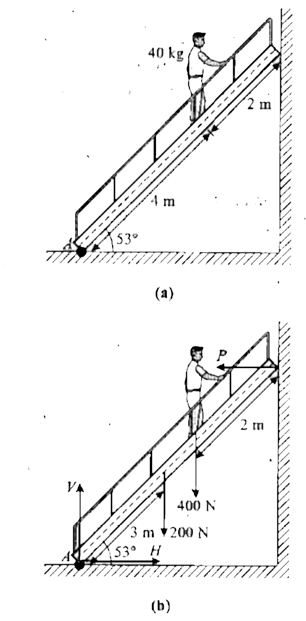
View SolutionCalculate the force P required to cause the block of weight `W_(2)=200N` just to slide under the block of weight `W_(1)=100N` shown in figure-2.43. What is the tension in the string AB and the normal forces acting between the blocks and that applied by ground on `W_(2)`? Surfaces of the blocks in contact are rough and the frictional force between the two blocks is 25 N and that between lower block and ground is 75 N Take `g = 10 m//s^(2)`.
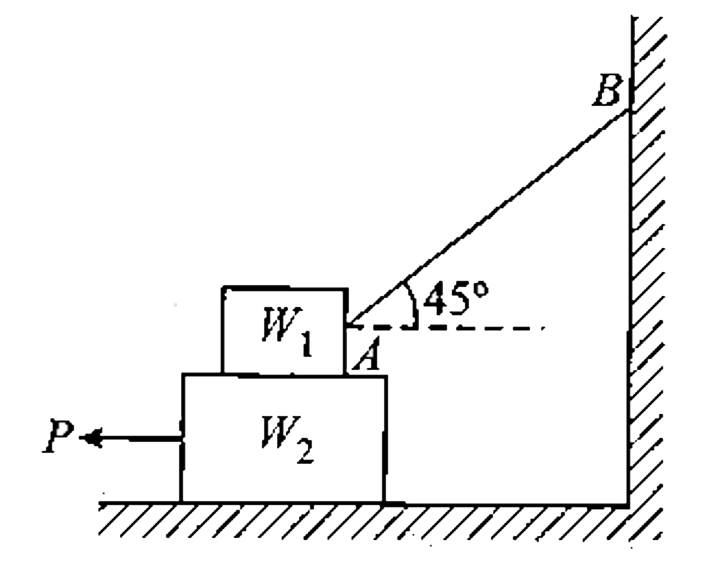
View SolutionFigure shows a light platform on which a man of mass M is standing and holding a string passing over a system of ideal pulleys. Another mass m is hanging as shown in fig. Find the force the man has to exert to maintain the equlibrium of system, and find the force exerted by the platform on the man. Also find the ratio of `M//m`.
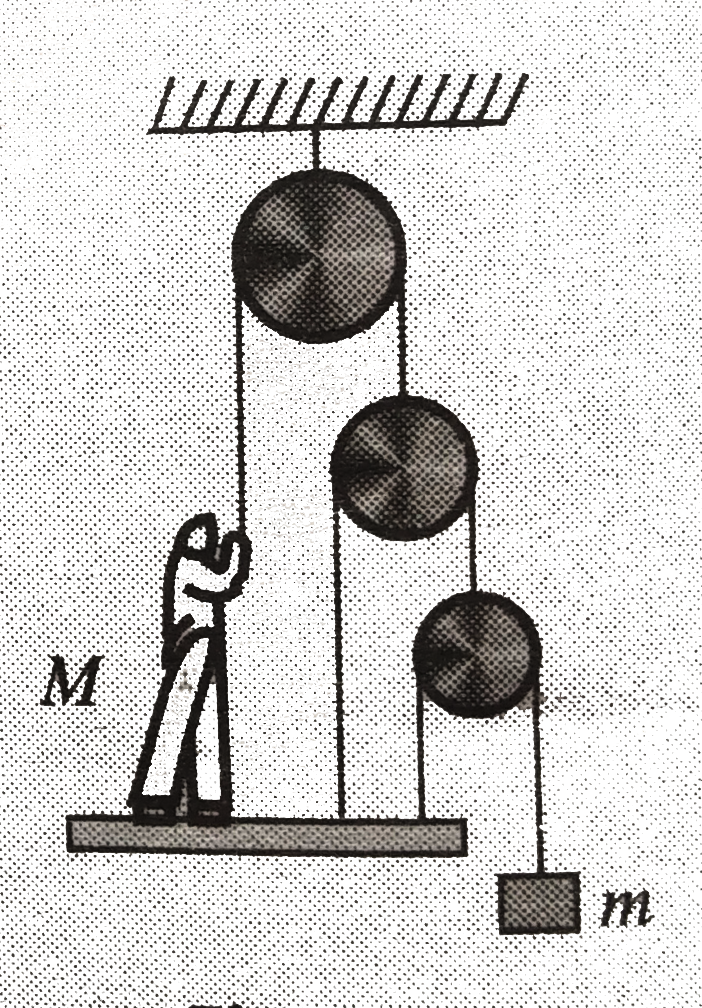
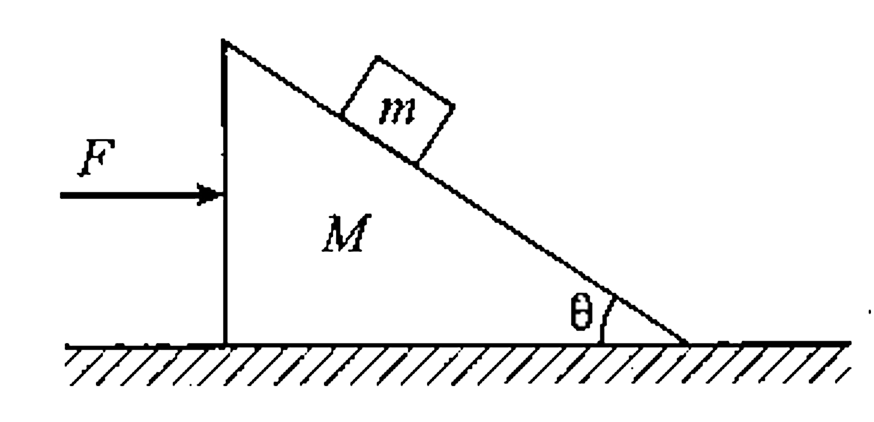
View SolutionFigure-2.52 shows a box of mass m is placed on a wedge of mass M on a smooth surface. How much force F is required to be applied on M so that during motion m remains at rest on its surface
View SolutionFigure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
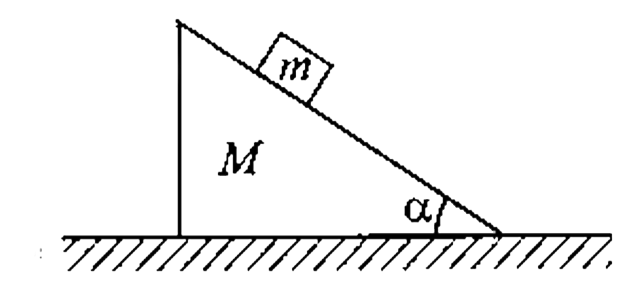
View SolutionFigure-2.57 shows a large block of mass M, supporting two small mass `m_(1)` and `m_(2)`, connected by a light, frictionless thread. A force F is acting on M, such that the block `m_(1)` is sliding down, with an acceleration `a_(1)`. Find the force F applied on M and also the acceleration of M. Assuming all surfaces are frictionless.
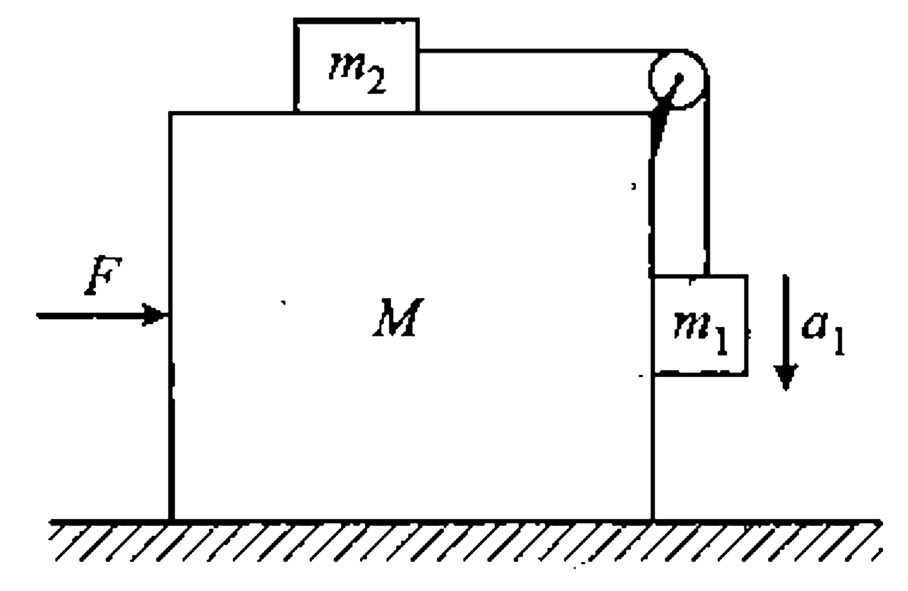
View SolutionFind the weight shown by the weighing machine on which a man of mass m is standing at rest relative to it as shown in figure-2.59. Assume that the wedge of mass M is in free fall.

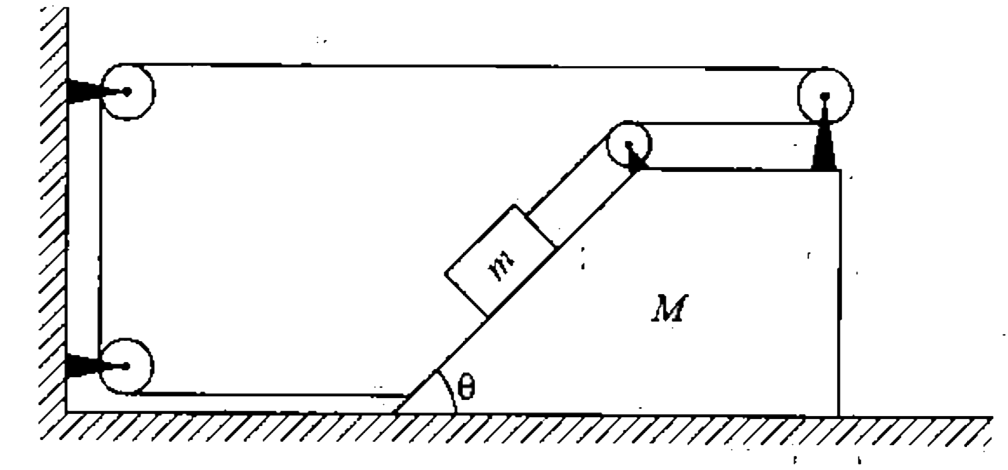
View SolutionIn the figure-2.61 a bar of mass m is on the smooth inclined face of the wedge of mass M,the inclination to the horizontal being 0.The wedge is resting on a smooth horizontal plane.Assuming the pulley to be smooth and the string is light and inextensible. Find the acceleration of M,when M and m are always in contact.

View SolutionFigure-2.64 shows a block of mass M supporting a bar of mass m through a pulley system. If system is released from rest, find the acceleration of block M and the tension in the strings
View SolutionA `100 kg` load is uniformly moved over a horizontal plane by a force F applied at an angle `30^(@)` to the horizontal. Find this force if the coefficient of friction between the load and the plane is 0.3. Take `g = 10m//s^(2)`
View SolutionConsider the situation shown in figure. The block `B` moves on a frictionless surface ,while the coefficient of friction between `A` and the surface on which it moves is `0.2`. Find the acceleration with which the masses move and also the tension in the strings. `(Take g = 10 m//s^(2))`.

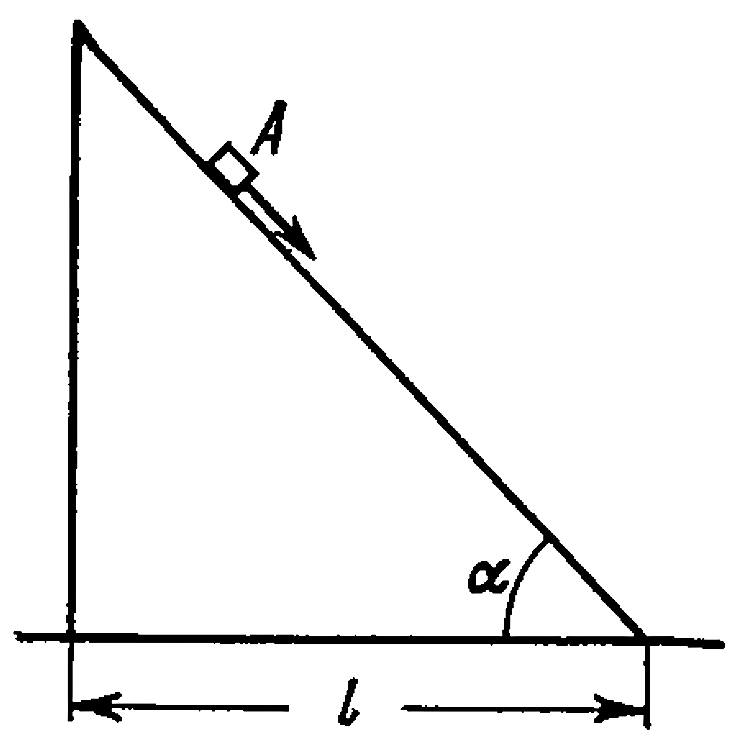
View SolutionA small body A starts sliding down from the top of a wedge (figure) whose base is equal to `l=2.10m`. The coefficient of friction between the body and the wedge surface is `k=0.140`. At what value of the angle `alpha` will the time of sliding be the least? What will it be equal to?
View SolutionA block slides down a rough inclined plane of slope angle `theta` with a constnat velocity. It is then projected up the same plane with an intial velocity v the distance travelled by the block up the plane coming to rest is .
View SolutionTwo blocks of masses `m_(1)` and `m_(2)` respectively are connected by an inextensible and weight less string which passes over a smooth and light pulley fixed at the top comer of a long carriage.The upper surface of the carriage is friction less and the body `Å` rests on it. B hangs vertically in contact with the rough vertical side of the carriage. The carriage moves with an acceleration gH towards right hand side as shown in figure-2.79. If the blocks remain stationary with respect to the carriage and `m_(1) = 7.5 m_(2)`, calculate the coefficient of friction between the block B and vertical side of the carriage.
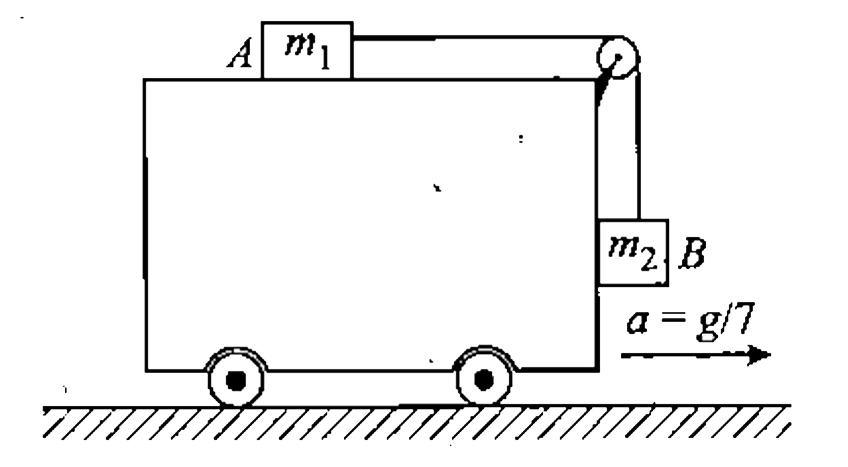
View SolutionA plank of mass `m_1` with a bar of mass `m_2` placed on it lies on a smooth horizontal plane. A horizontal force growing with time t as `F^'=at` (a is constant) is applied to the bar. Find how the accelerations of the plank `w_1` and of the bar `w_2` depend on t, if the coefficient of friction between the plank and the bar is equal to k. Draw the approximate plots of these dependences.
View SolutionA bar of mass `m` is placed on a triangular block of mass `M` as shown in figure The friction coefficient between the two surface is `mu` and ground is smooth find the minimum and maximum horizontal force `F` required to be applied on block so that the bar will not slip on the inclined surface of block

View SolutionTwo masses `m_(1)` kg and `m_(2)` kg passes over an atwoods machine. Find the ratio of masses `m_(1)` and `m_(2)` so that string passing over the pulley will just start slipping over its surface. The friction coefficient between the string and pulley surface is 0.2.
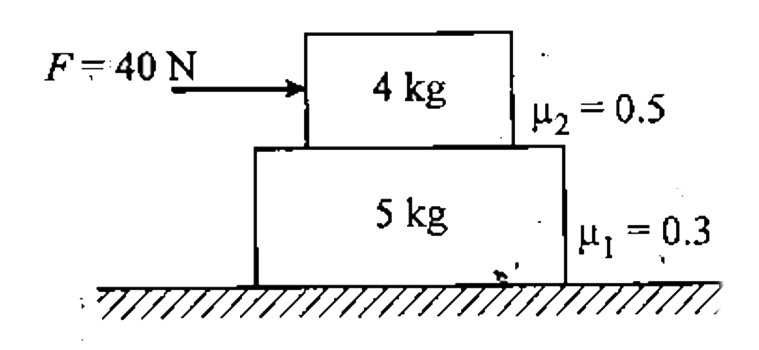
View SolutionFind the acceleration of the two blocks of 4 kg and 5 kg mass if a force of 40 N is applied on 4 kg block. Friction coefficients between the respective surface are shown in figure-2.92. Take `g = 10 m//s^(2)`
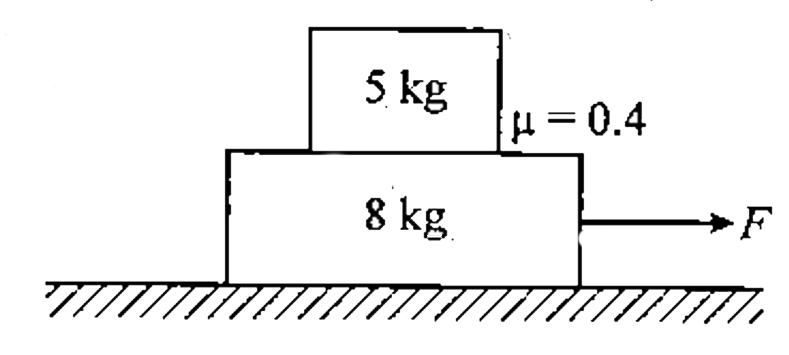
View SolutionFind the maximum possible force which can be applied to the 8 kg block shown in figure-2.94 to move both the blocks together if bottom surface is (a) frictionless, (b) having friction coefficient 0.3. Take `g = 10m//s^(2)`
View SolutionIn the sitution shown in figure there is no friction between `2 kg` and ground.

a. For what maximum value of force `F` can all three blocks move together?
b. Find the value of force `F` at which sliding starts at other rough surfaces.
c. Find acceleration of all blocks, nature and value of friction force for the following values of force `F` (i) `10N` (ii) `N` and (iii) `25 N`
View SolutionIn the situation shown in figure-2.99.
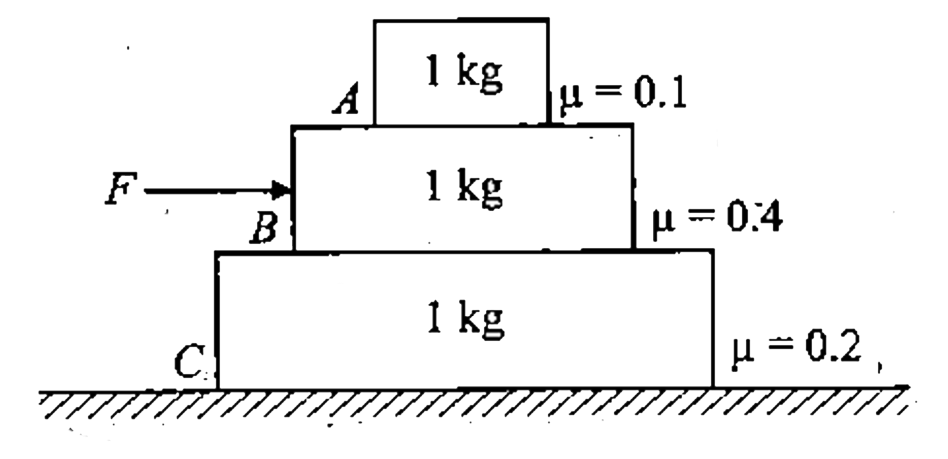
(a) For what minimum value of the force F will the system or any part of it start to move ?
(b) Find the values of force F when slipping starts between (i) A and B and (ii) B and C. Take `g = 10m//s^(2)`
View SolutionFigure-2.107 shows a block of mass m attached to a spring of force constant k and connected to ground by two string of equal lengths making an angle `90^(@)` with each other. In relaxed state natural length of the spring is l. In the situation shown in figure, find the tensions in the two strings.
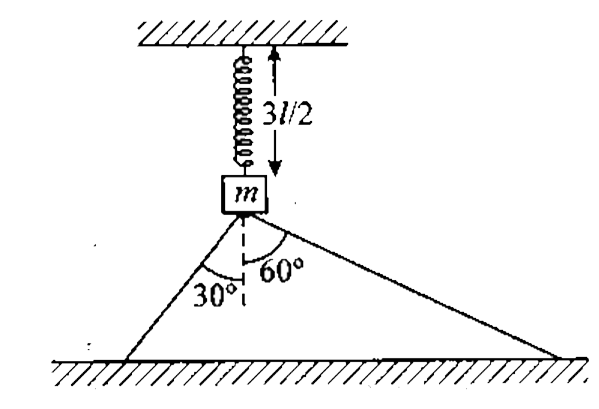
View SolutionFigure-2.109 shows a block A on a smooth surface attached with a spring of force constant k to the ceiling. In this state spring is in its natural lengthl. The block A is connected with a massless and frictionless string to another identical mass B hanging over a light and smooth pulley. Find the distance moved by A before it leaves contact with the ground
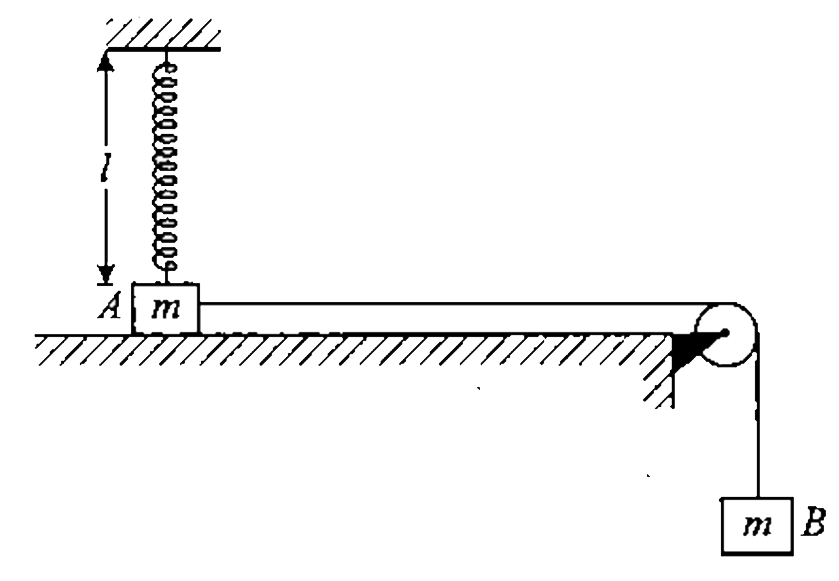
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of lengths `l//3` and `2l//3`, and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure-2.111. Find the stretch in each of the spring.
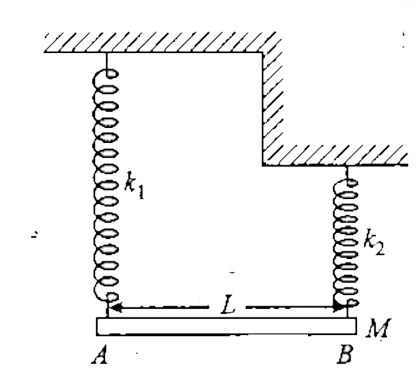
View SolutionFind the stretch in the springs shown in figure-2.112. The respective data are given in the figure. The friction and masses in pulleys are negligible.
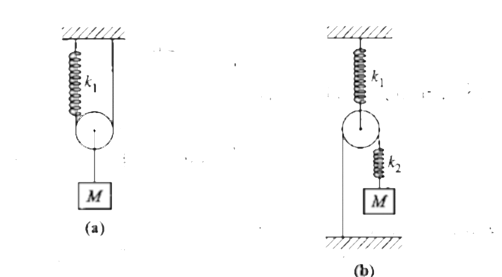
View SolutionFind the readings of spring balances `S_(1),S_(2)` and `S_(3)` of the springs shown in figure-2.115(a). If the string snaps at point A find the readings of the three spring balances just after the string snaps. All pulleys and strings are ideal.
View Solution(a) Find the acceleration of the three masses shown in figure-2.116(a) and the extension in the spring. The force constant of the spring is 100 N/m. Assume all strings and pullies are ideal.
(b) Find the acceleration of the masses A and B just after the string snaps at P but in this case the spring is replaced by a string. Take `g = 10m//s^(2)`
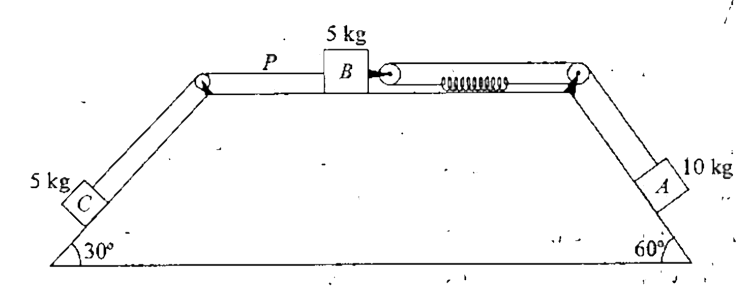
View Solution
Illustravtive Example questions and complete solutions for chapter NEWTONS LAWS OF MOTION of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11