Complete Solutions to Numerical MCQs of chapter NEWTONS LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION |
| PHYSICS GALAXY | Numerical MCQs |
| Number Of Questions | 90 |
| Academic Year | 2023-24 |
Two blocks `A & B` attached to each other by a mass-less spring, are kept on a rough horizontal surface `mu=0.1`. A constant force `F=200 N` is applied on blcok `B` horizon tally as shown below. If a some instant the acceleration of `10 kg` mass is `12 m//s^(2)`, then the acceleration of `20 kg` mass is
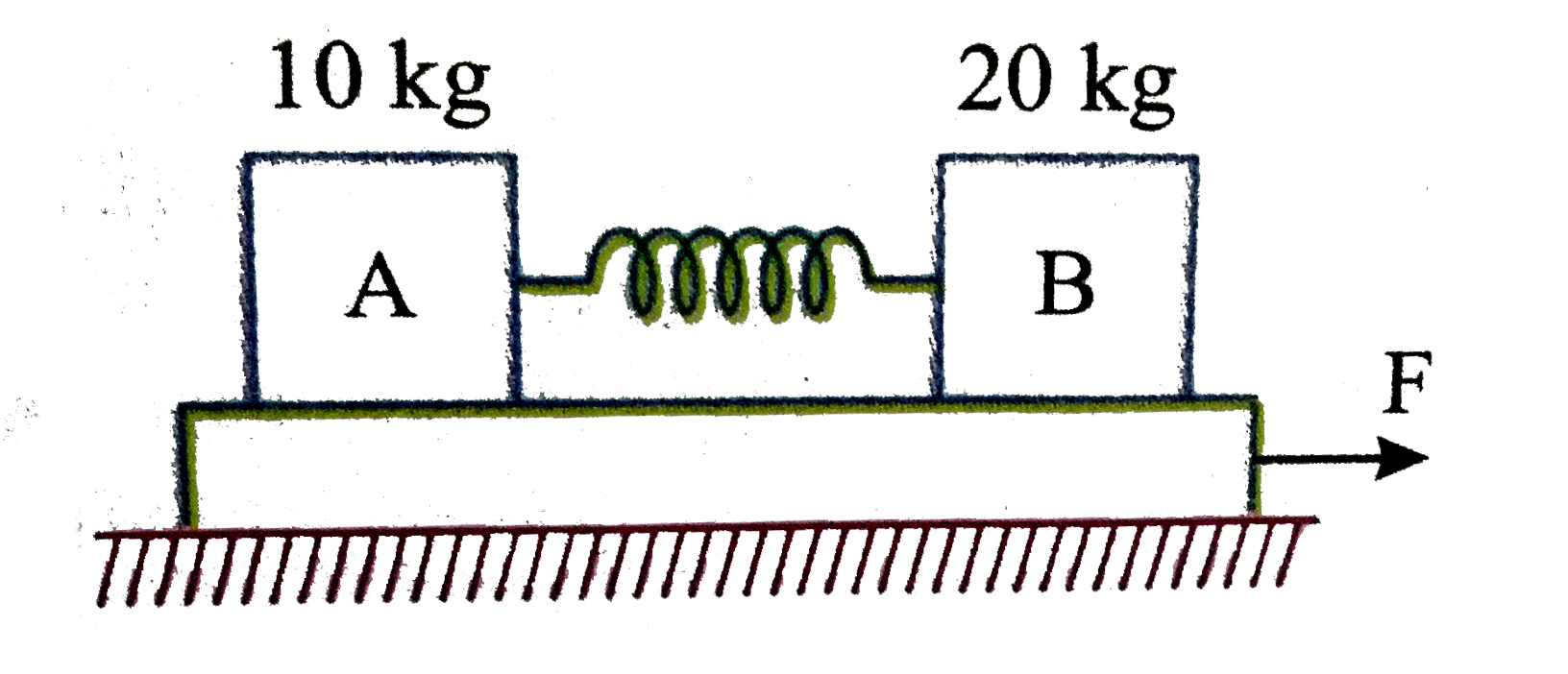
View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is `mu`. What is the minimum acceleration of the cart so that the block m does not fall ?

View SolutionA body of mass `m` is kept on a rough fixed inclined plane of angle of inclination `theta=30^(@)`. It remains stationary. Then magnitude of force acting on the body by the inclined plane is equal to `:`
View Solution
Two blocks A (1 kg) and B (2 kg) are connected by a string passing over a smooth pulley as shown in the figure. B rests on rough horizontal surface and A rest on B. The coefficient of friction between A and B is the same as that between B and the horizontal surface. The minimum horizontal force F required to move A to the left is 25 N. The coefficient of friction is:
View SolutionA particle moving on the inside of a smooth sphere of radius r describing a horizontal circle at a distance `r//2` below the centre of the sphere. What is its speed ?
View SolutionIn the system of pulleys shown what should be the value of `m_(1)` such that 100 gm remains at rest : (Take `g = 10 m//s^(2)`)
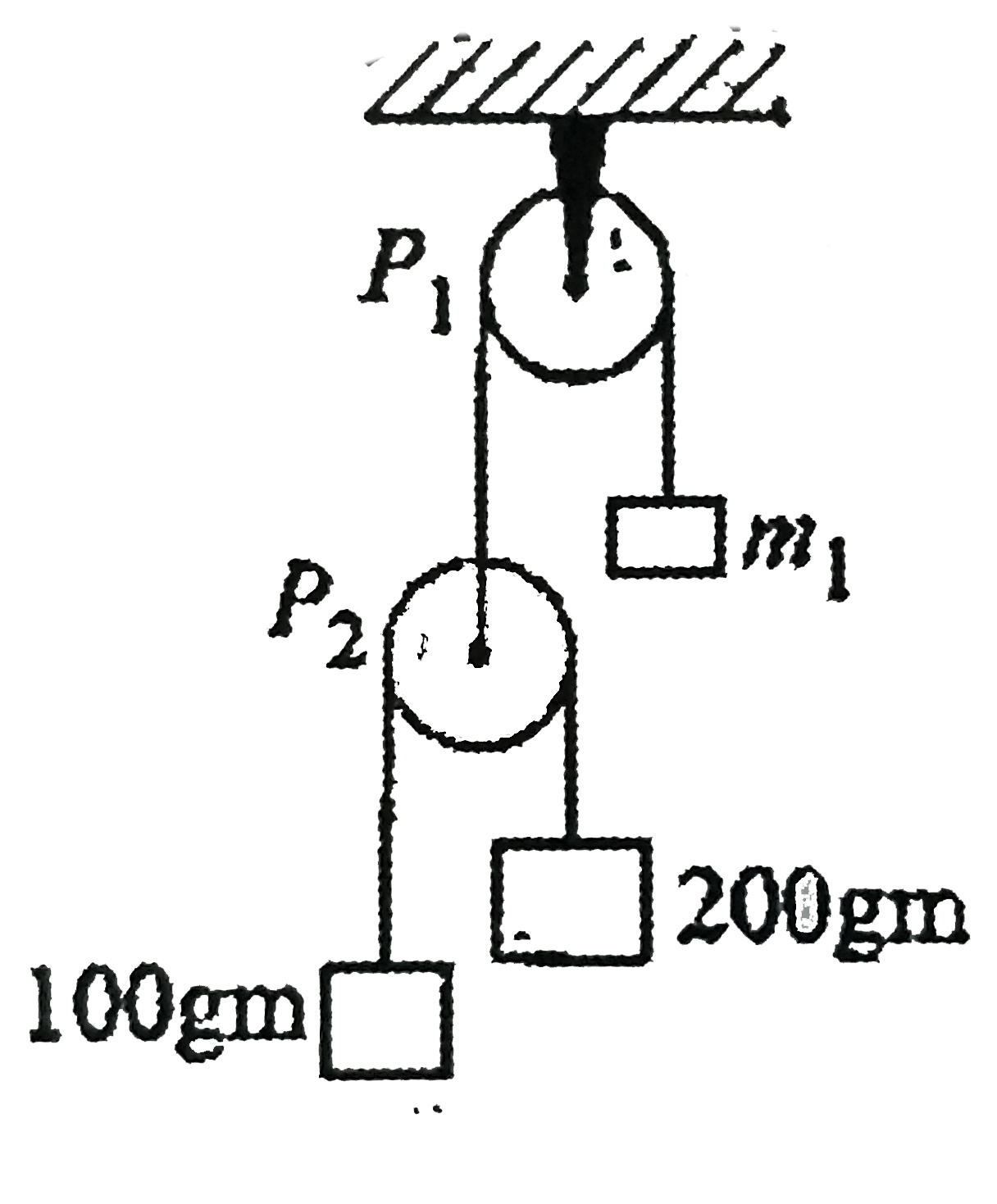
View SolutionA body of mass M is kept on a rough horizontal surface (friction coefficient `= mu`). A person is trying to pull the body by applying a horizontal force but the body is not moving. The force by the surface on the body is F where :
View Solution
In the figure, at the free end of the light string, a force F is spplied to keep the suspended mass of 18 kg at rest. Then the force exerted by the cirling on the system (assume that the string segments are vertical and the pulleys are light and smooth) is:(`g=10(m)/(s^2)`)
View SolutionA ball weighing `10g` hits a hard surface vertically with a speed of `5m//s` and rebounds with the same speed The ball remains in contact with the surface speed The ball remains in contact with the surface for `0.01s` The average force exerted by the surface on the ball is .
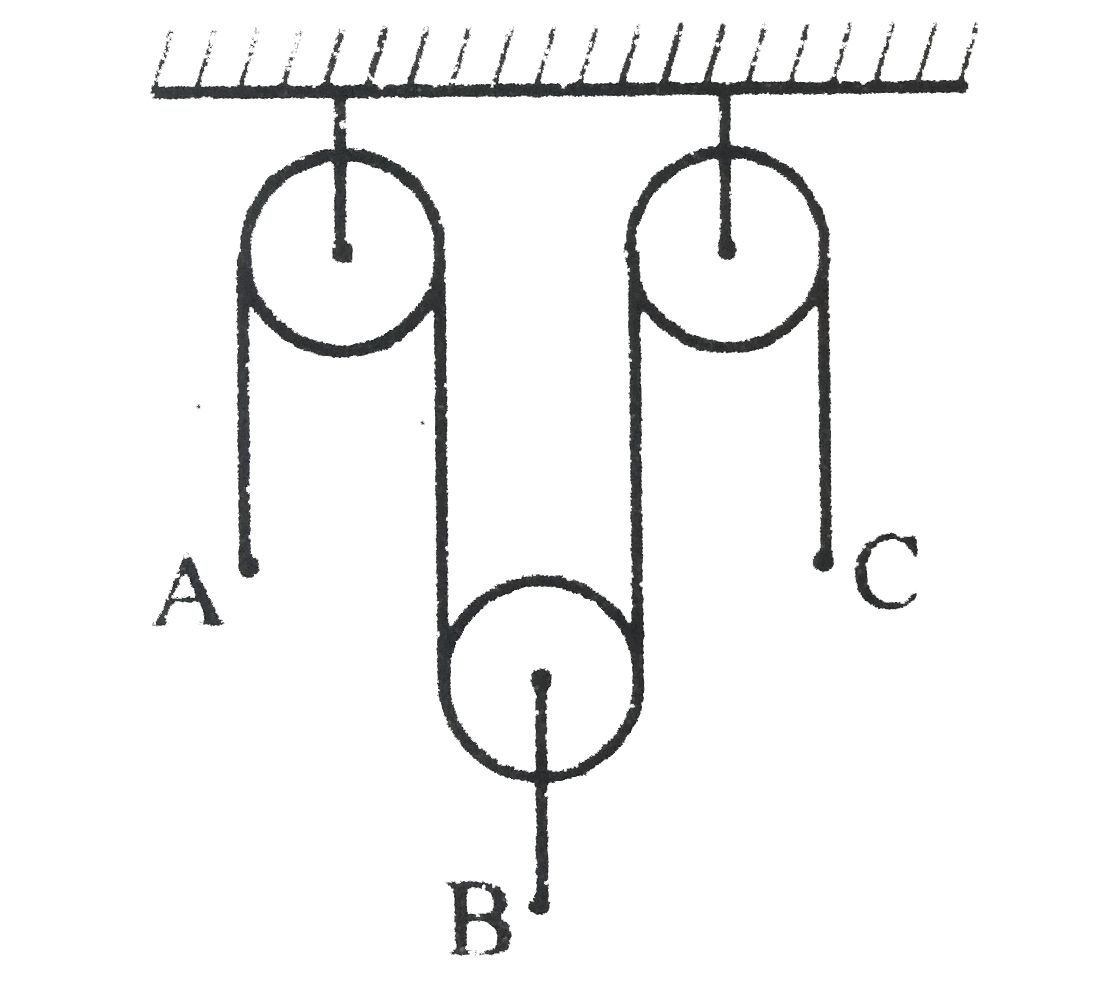
View SolutionThe pulley in the diagram are all smooth and light. The acceleration of `A` is `a` upwards and the acceleration of `C` is `f` downwards. The acceleration of `B` is
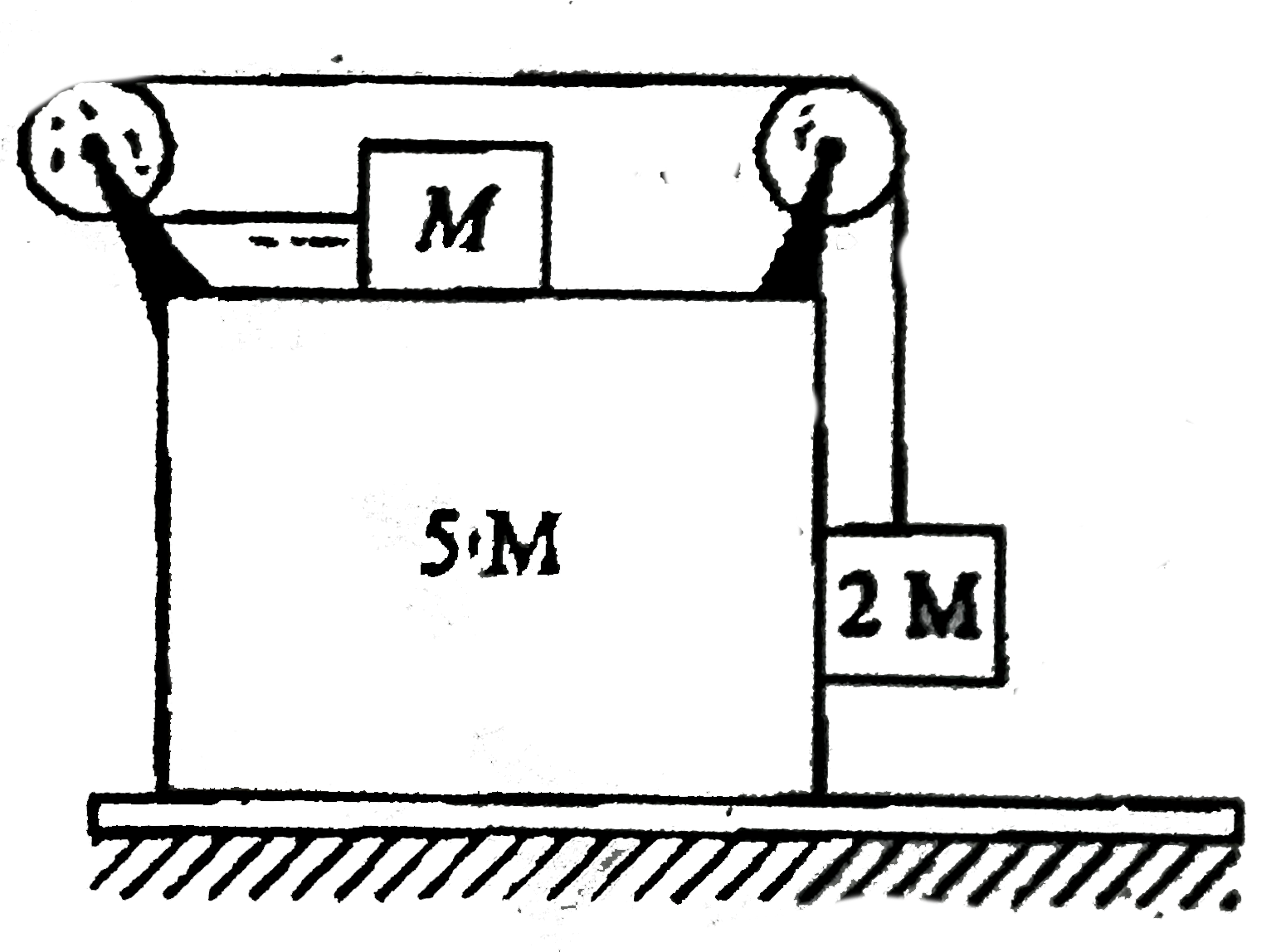
View SolutionIn the system shown, the initial acceleration of the wedge of mass 5M is (there is no friction anywhere)
View SolutionFind the acceleration of 3 kg mass when acceleration of 2 kg mass is `2ms^(-2)` as shown in figure-2.140
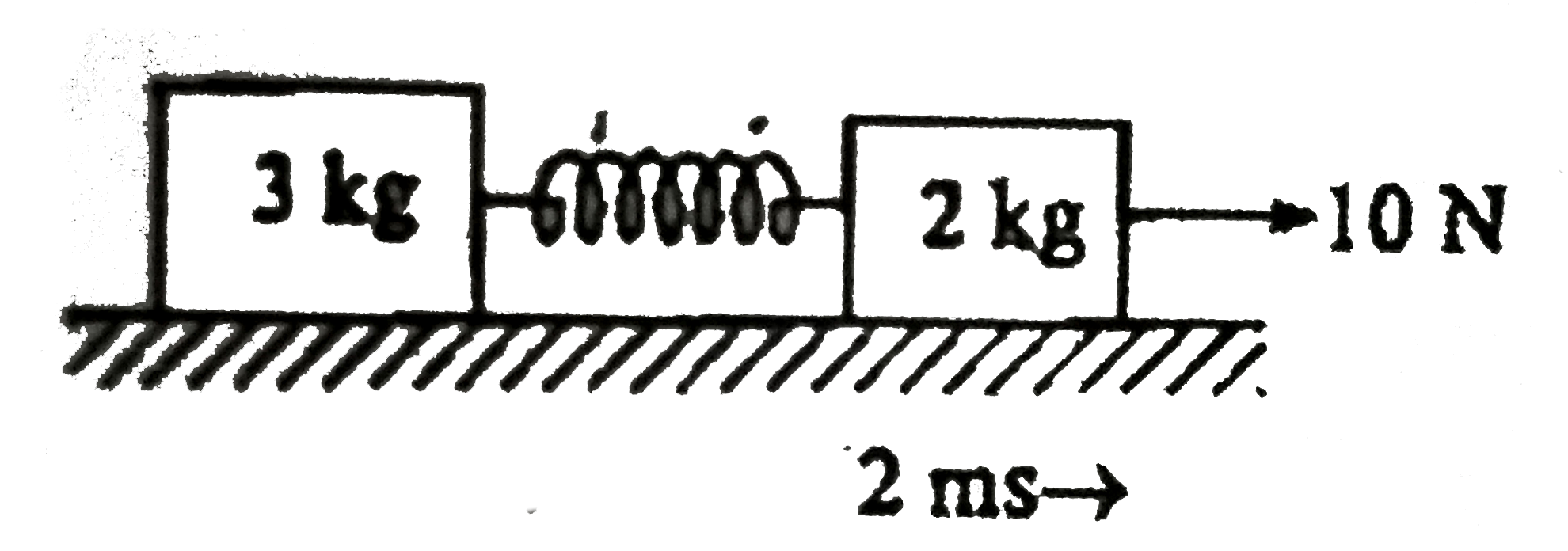
View SolutionForce F is applied on upper pulley. If F = 30 t where t is time in second. Find the time when `m_(1)` loses contact with floor : (Take `g = 10 m//s^(2)`)
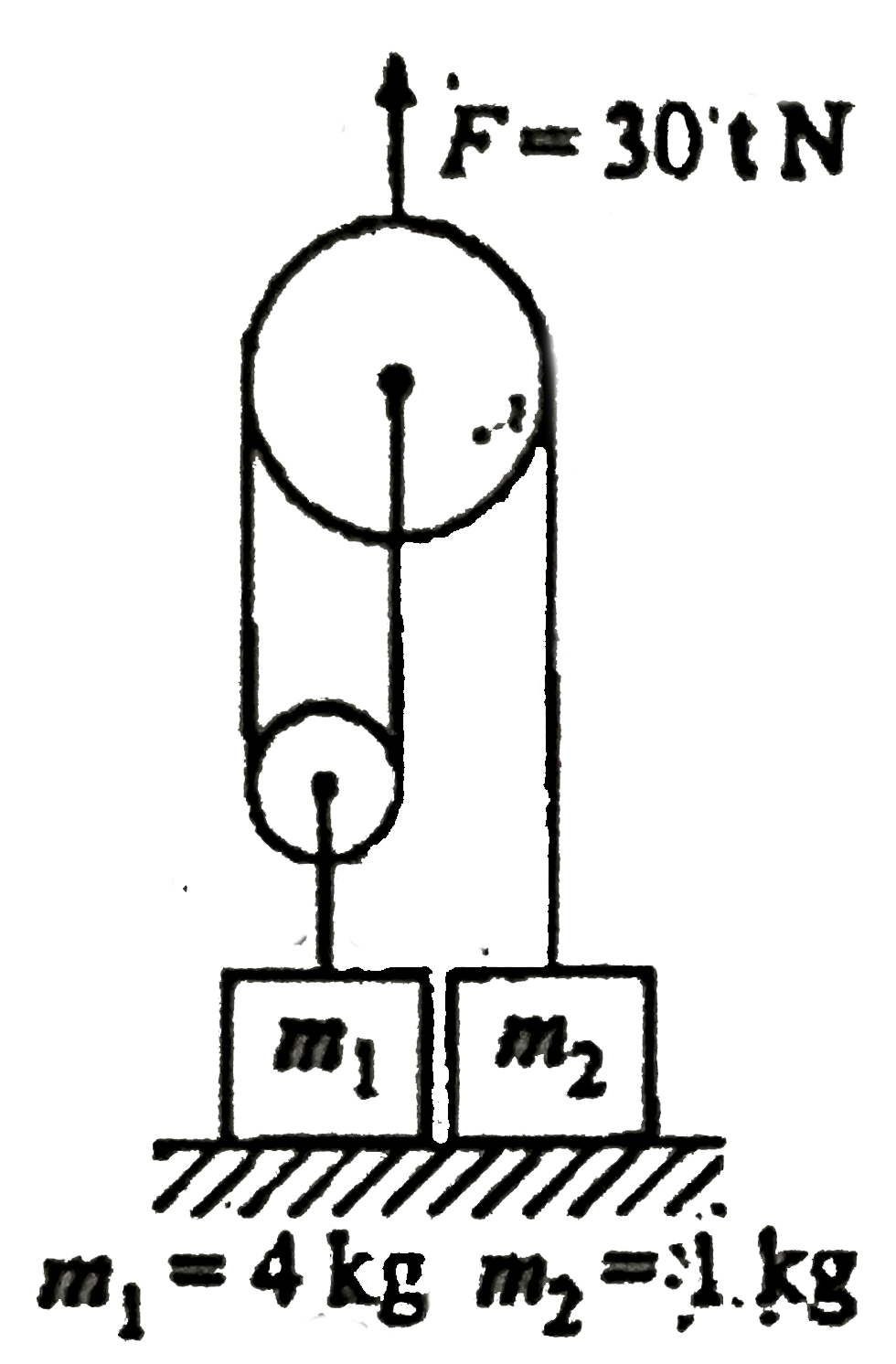
View SolutionA varying horizontal force `F =` at acts on a block of mass `m` kept on a smooth horizontal surface An identical block is kept on the first block.The coefficient of friction between the blocks is `mu` . The time after which the relative sliding between the blocks prevails is
View SolutionThe system shown is just on the verge of slipping. The coefficient of static friction between the block and the table top is :
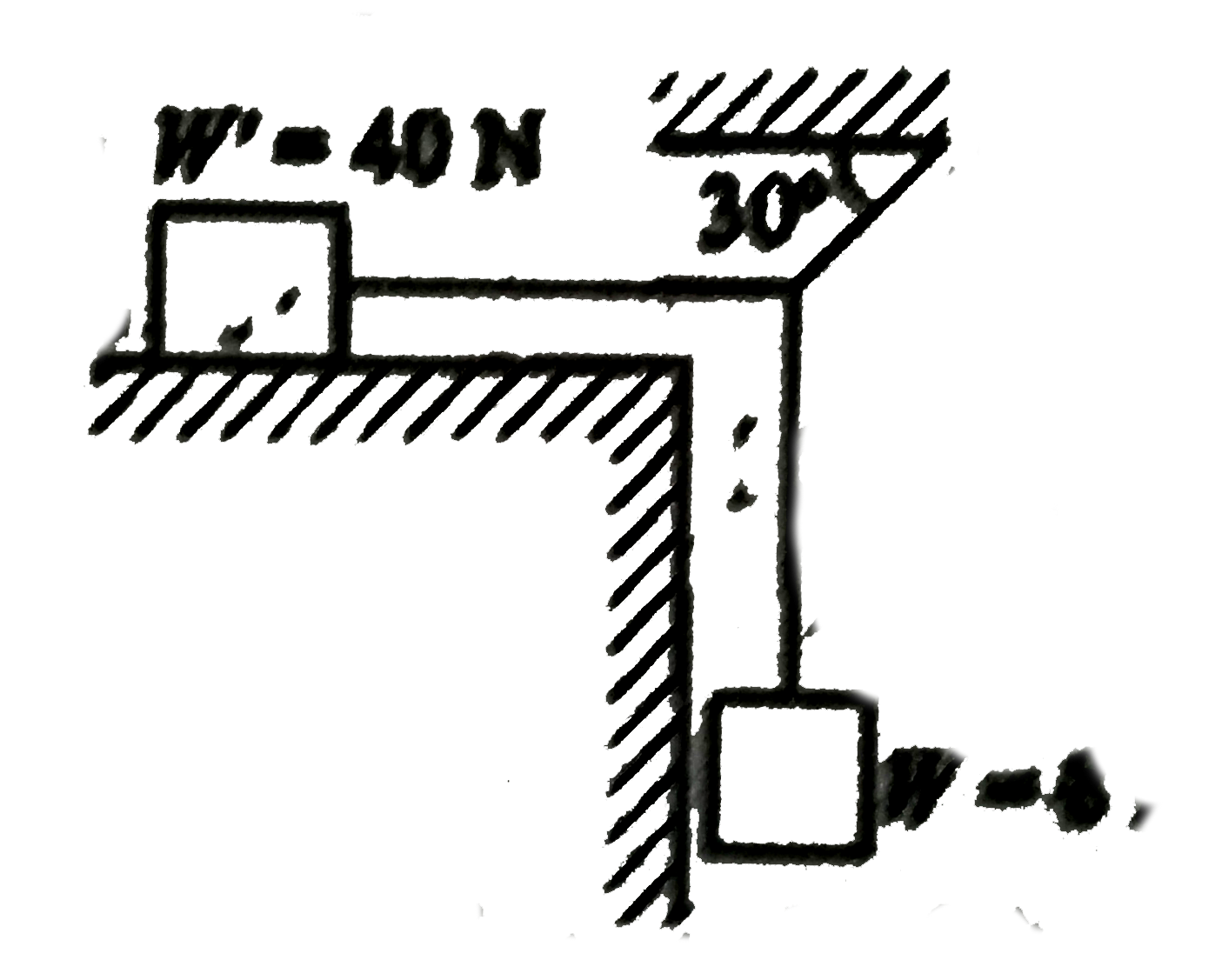
View SolutionA body is moving down a long inclined plane of angle of inclination `theta`. The coefficient of friction between the body and the plane varies as `mu - 0.1 x`, where x is the distance moved down the plane. The body will have the maximum velocity when it has travelled a distance x given by :
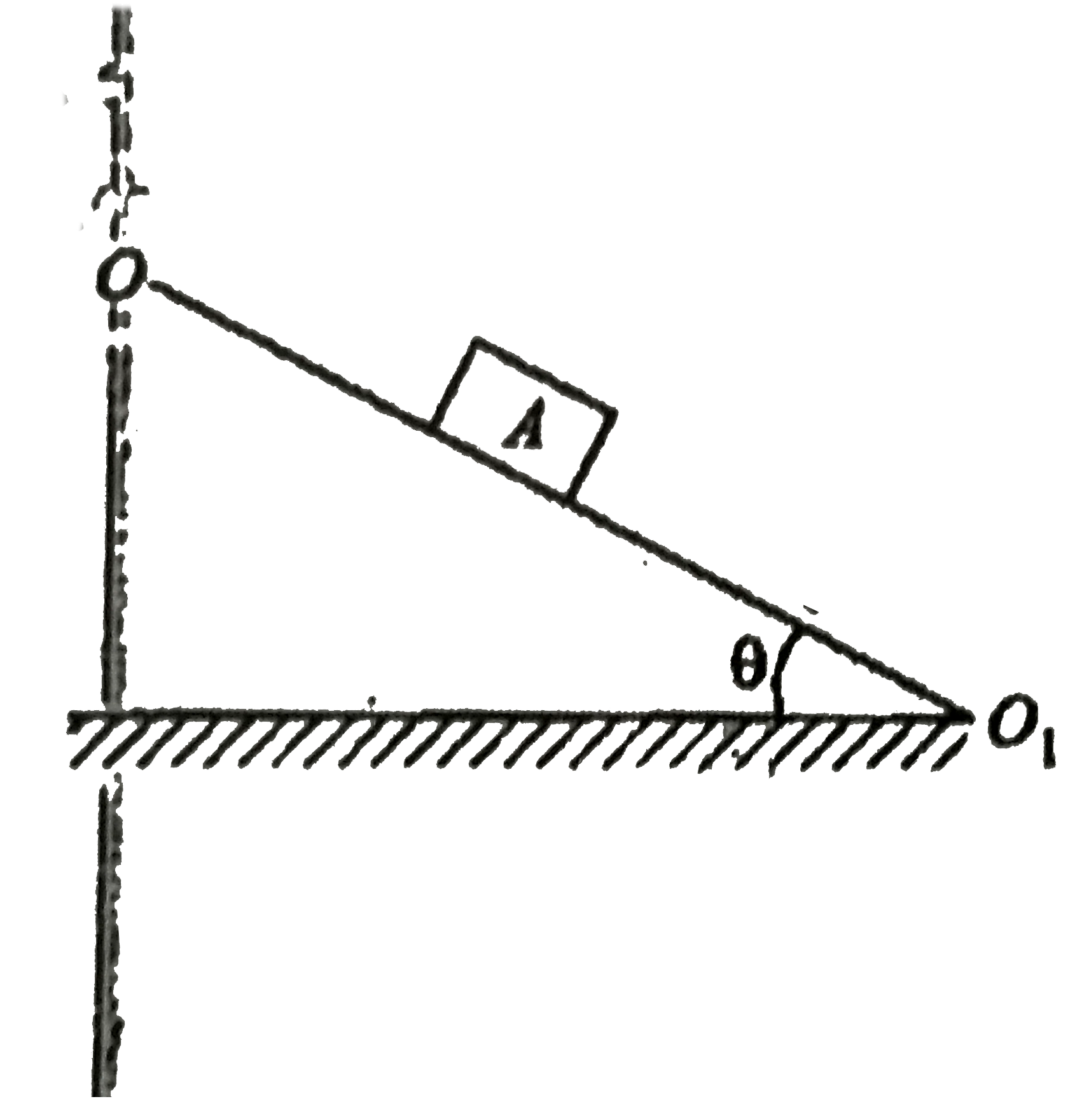
View SolutionA block A kept on a rough plate `(OO_(I))` with coefficient of static friction `mu_(s)=0.75` & coefficient of kinetic friction `mu_(hat(k))=0.5`. The plate is leaning with horizontal at an angle `theta=tan^(-1)(mu'_(s))`. If the plate is further tilted slightly then the acceleration of block will be :
View SolutionFor a particle rotating in a vertical circle with uniform speed, the maximum and minimum tension in the string are in the ratio 5 : 3. If the radius of vertical circle is 2 m, the speed of revolving body is (`g=10m//s^(2)`)
View SolutionBlock M slides down on frictionless incline as shown. The minimum friction coefficient so that m does not slide with respect to M would be :
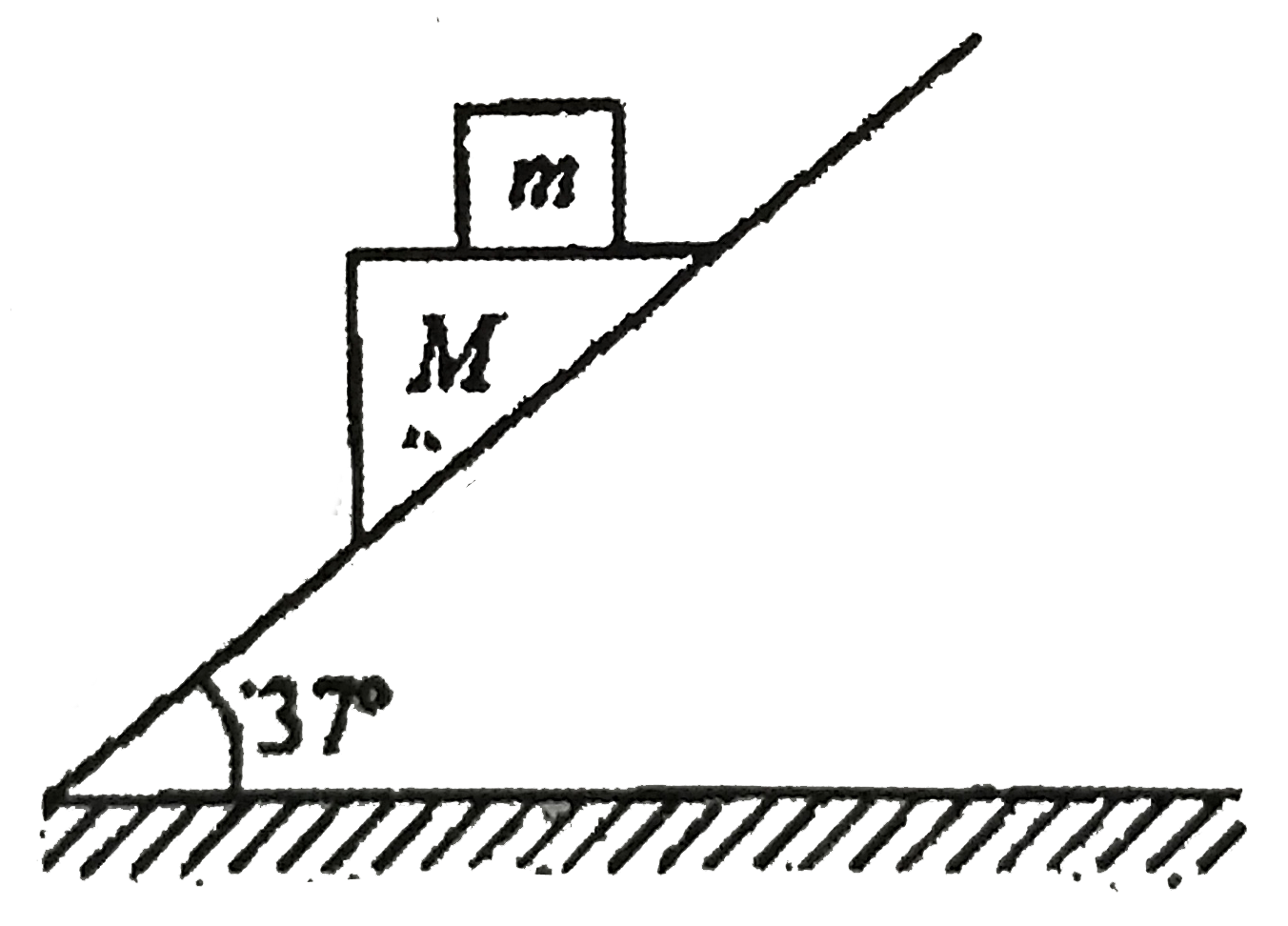
View SolutionA force `F = Be^(Ct)` acts on a particle whose mass is m and whose velocity is 0 at t = 0. It's terminal velocity is :
View SolutionIn the figure shown neglecting friction and mass of pulley, what is the acceleration of mass `B` ?
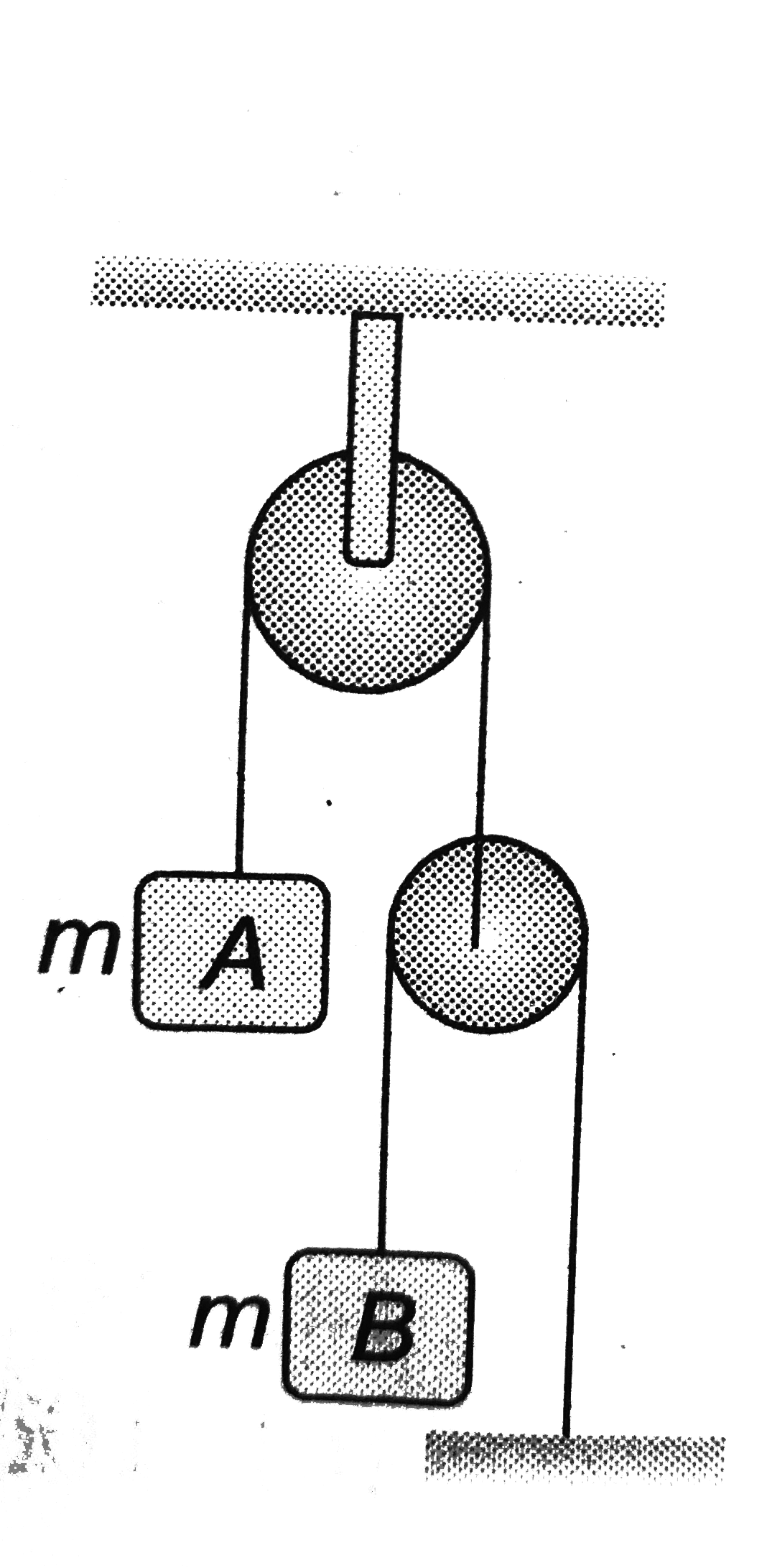
View SolutionTwo bodies of mass m and 4m are attached by a string shown in the figure-2.146. The body of mass m hanging from a string of length l is executing simple harmonic motion with amplitude A while other body is at rest on the surface. The minimum coefficient of friction between the mass 4m and the horizontal surface must be to keep it at rest is :

View SolutionA spring of force constant k is cut into two pieces such that one piece is double the length of the other. Then the long piece will have a force constant of :
View SolutionA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?

View SolutionA car starts from rest to cover a distance s. the coefficient of friction between the road and the tyres is `mu`. The minimum time in which the car can cover the distance is proportional to
View SolutionThree equal weights of mass 3 kg each are hanging on a string passing over a fixed pulley as shown in figure-2.147. The tension in the string connecting weight B and C is : (Take `g = 10m//s^(2)`)
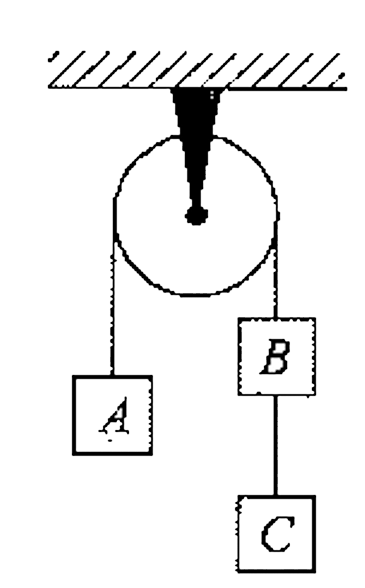
View SolutionA block of mass` m_(1) = 1 kg` is horizontally thrown with a velocity of `v = 10 m//s` on a statonary long plank of mass`m_(2) = 2 kg` whose surface has `mu = 0.5 ` plank rest on frictionless surface find the time when the block comes to rest w.r.t plank

View SolutionA board of mass m = 1 kg lies on a table and a weight of M = 2 kg on the board. What minimum force F must be applied on the board in order to pull it out from under the road ? The coefficient of friction between board and table is `mu_(2) = 0.5` : (Take `g = 10 m//s^(2)`)
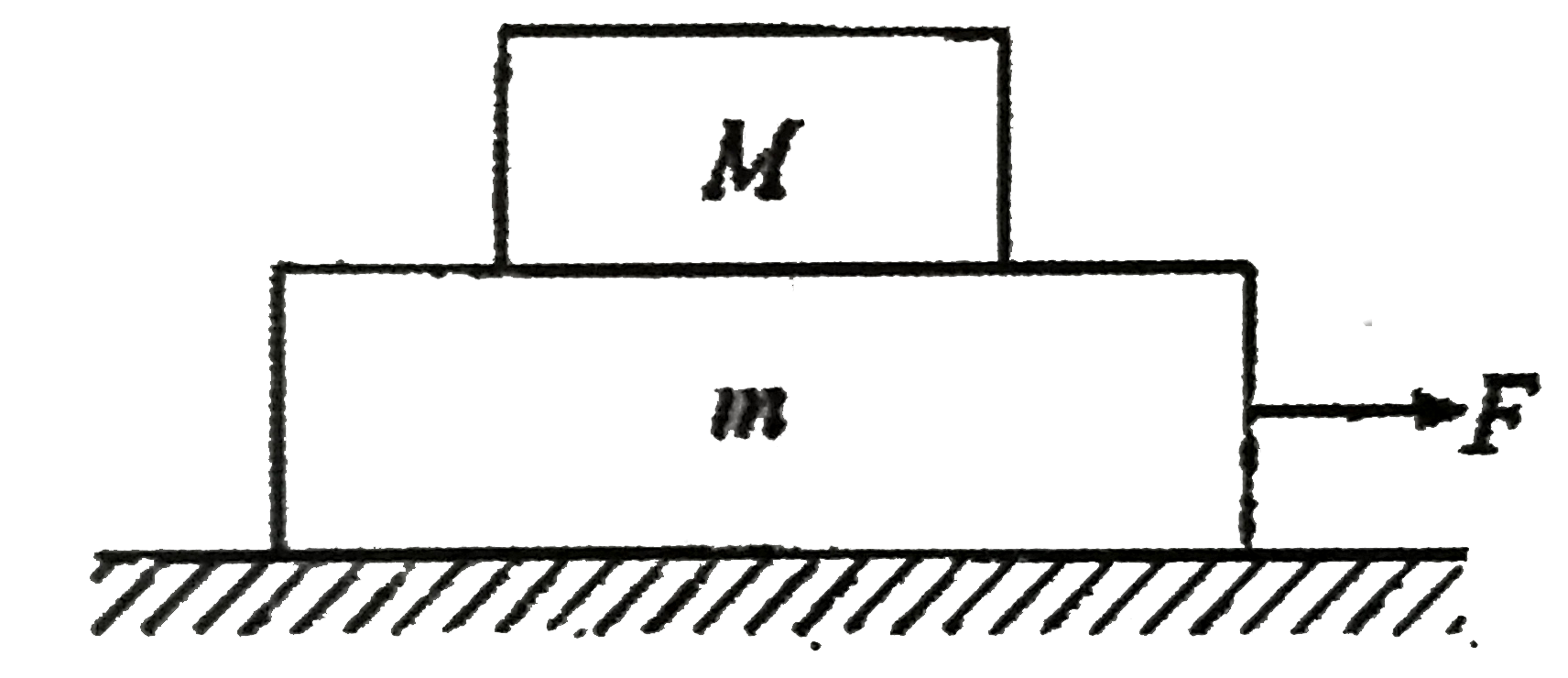
View SolutionA man is standing in a lift which goes up and comes down with the same constant acceleration. If the ratio of the apparent weights in the two cases is `2 : 1` , then the acceleration of the lift is : (Take `g = 10 m//s^(2)`)
View SolutionA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force `F` is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is

View SolutionIn the shown mass pulley system, pulleys and string are massless. The one end of the string is pulled by the force F = mg. The acceleration of the block will be :

View SolutionA block is given certain upward velocity along the incline of elevation `alpha`. The time of ascent to upper point was found to be half the time of descent to initial point. The co-efficient of friction between block and incline is :
View SolutionConsider the shown arrangement. The coefficient of friction between the two blocks is 0.5 . There is no friction between the 4 kg block and of 12 N is applied on the 2 kg block as shown in the figure, the acceleration of the 4 kg block would be

View Solution
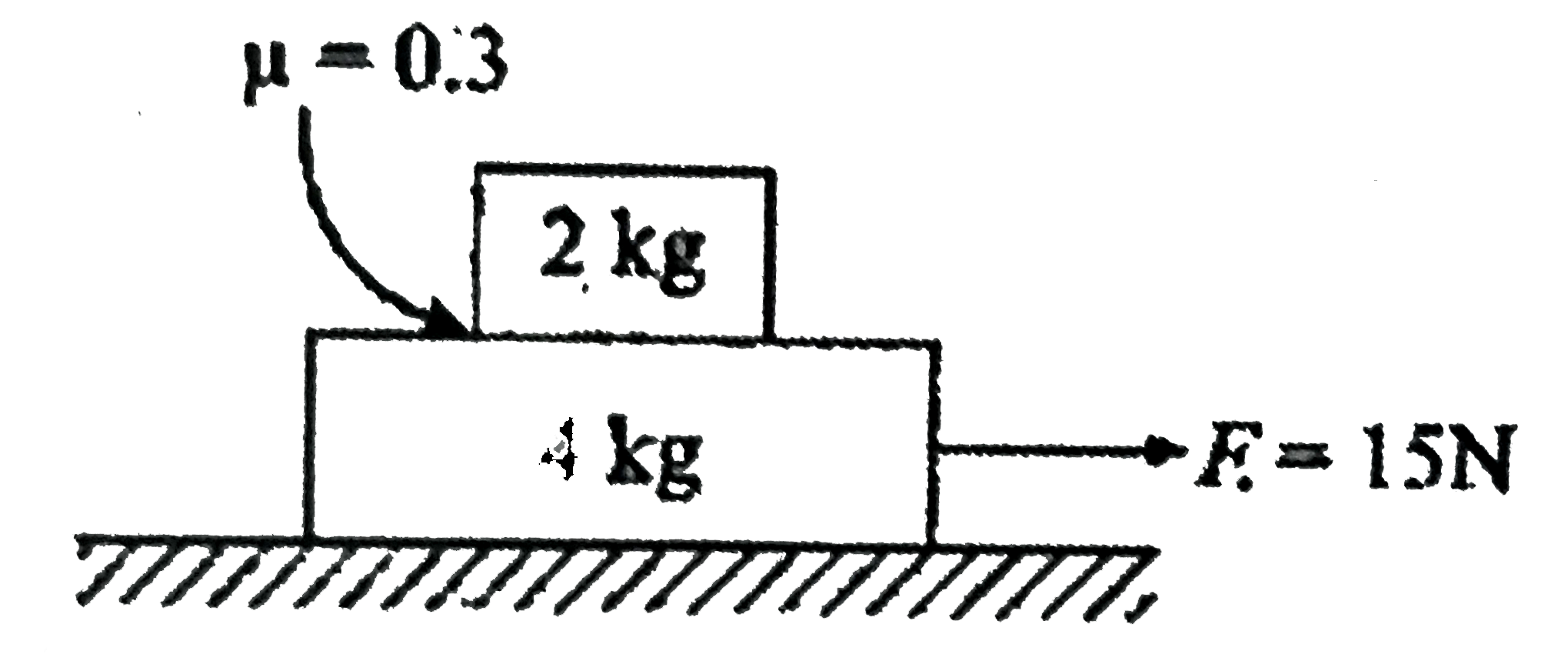
A 40 kg slb rest on a frictionless floor as shown in the figure. A 10 kg block rests on the top of the slab. The static corfficient of friction between the block and slab is 0.60 while the kinetic friction is 0.40 the 10 kg block is acted upon by a horizontal force 100N. If `g=9.8(m)/(s^2)`, the resulting acceleration of the slab will be.
View SolutionA load attached to the end of a spring and in equilibrium produces 9 cm extension of spring. If the spring is cut into three equal parts and one end of reach is fixed at 'O' and other ends are attached to the same load, the tension in cm of the combination in equilibrium now is :
View SolutionA heavy spherical ball is constrained in a frame as shown in figure-2.153. The inclined surface is smooth. The maximum acceleration with which the frame can move without causing the ball to leave the frame :
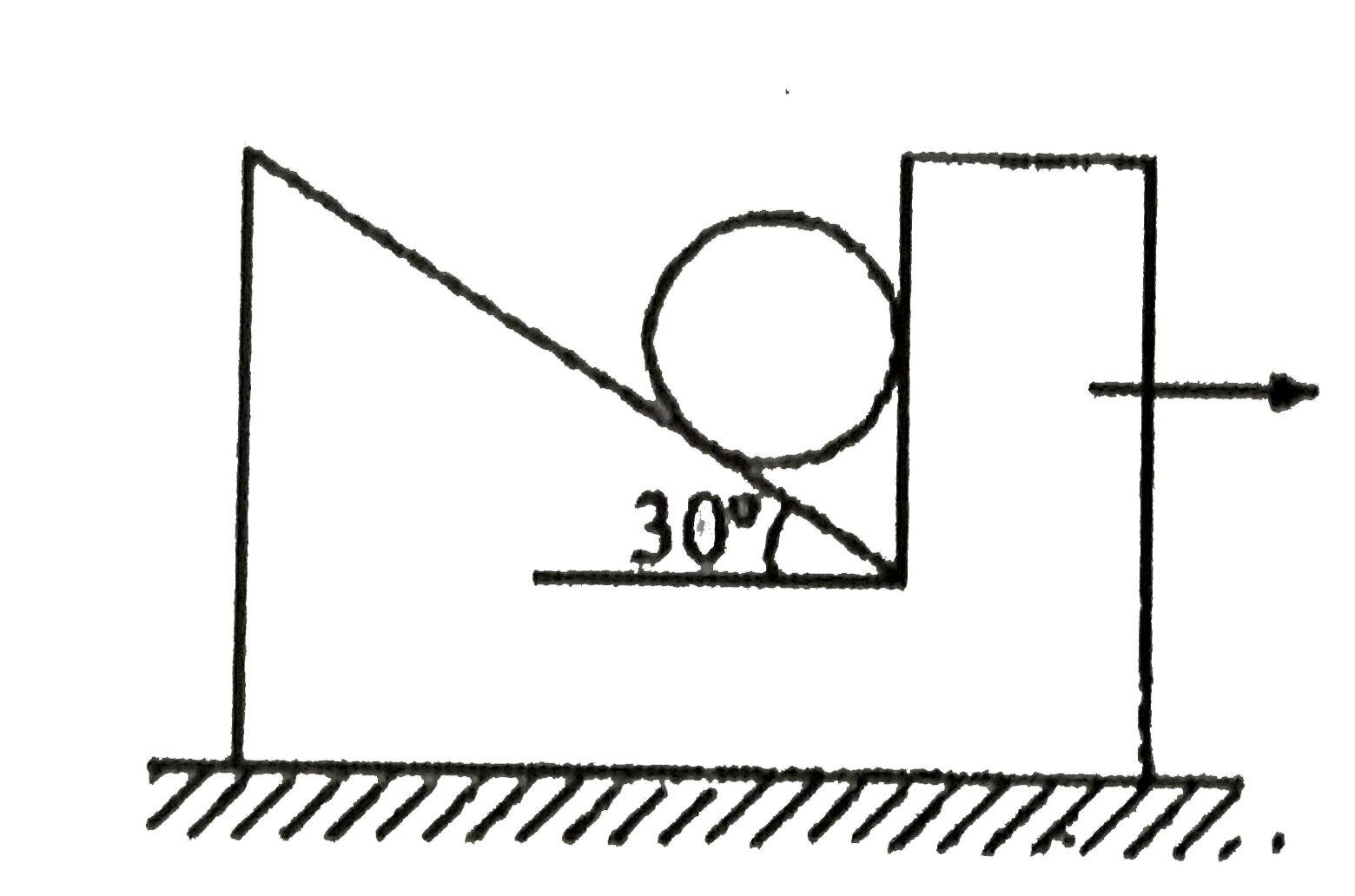
View SolutionFind the reading of spring balance as shown in figure-2.154. Assume that mass M is in equilibrium :

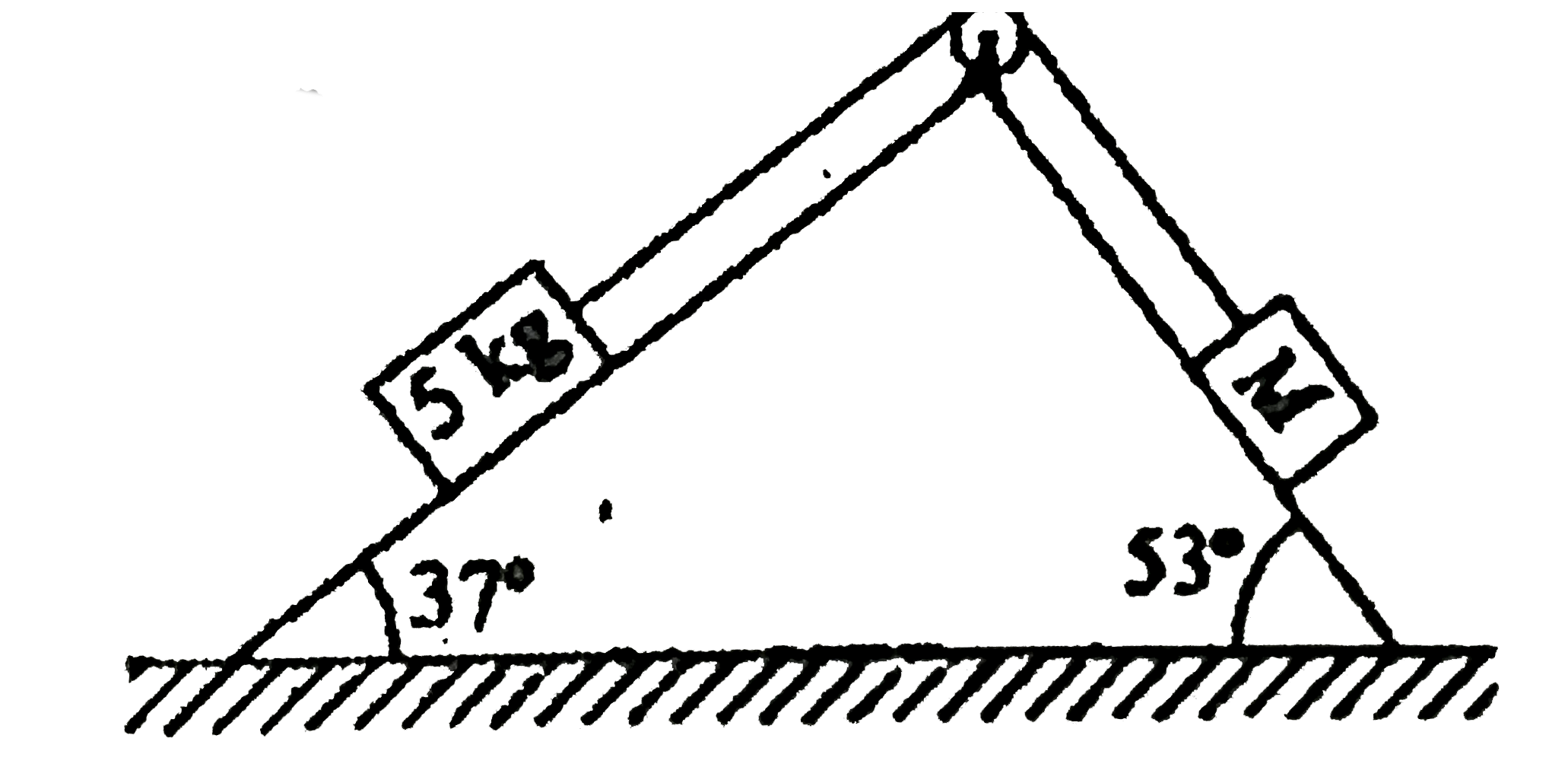
View SolutionFor what value of M will the masses be in equilibrium. Masses are placed on fixed wedge :
View SolutionA body of mass m starts sliding down an incline of `30^(@)` from rest. The body comes to rest just when it reaches the bottom. If the top half of the plane is perfectly smooth and the lower half is rough, find the force of friction :
View SolutionA mass of 0.5 kg is just able to slide down the slope of an inclined rough surface when the angle of inclination is `60^(@)`. The minimum force necessary to pull the mass up the incline along the line of greatest slope is : (Take `g=10m//s^(2)`)
View SolutionMinimum force required to keep a block of mass 1 kg at rest against a rough vertical wall is P. If a force `P//2` is applied then the acceleration of the block will be :
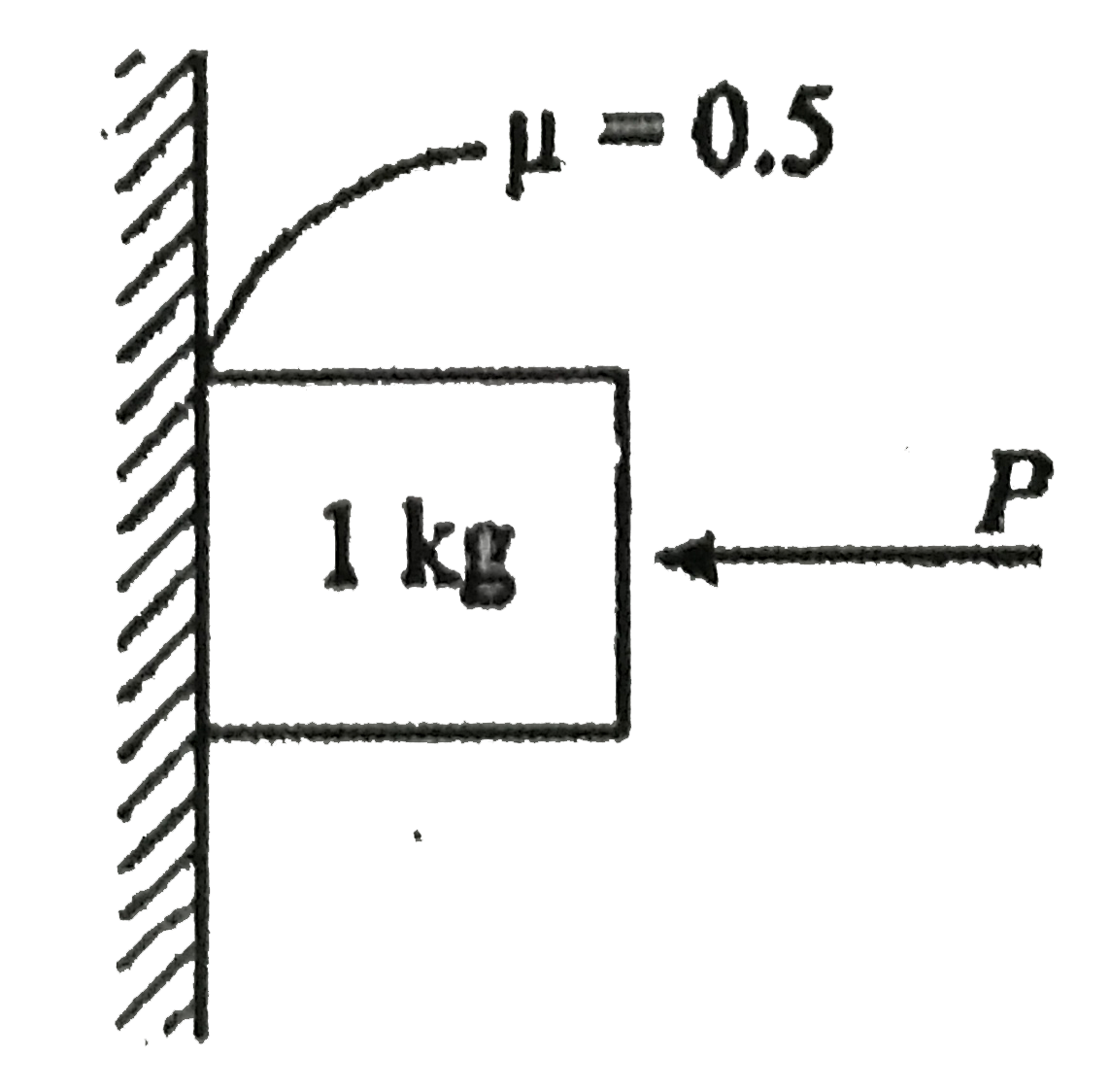
View SolutionA 60 kg body is pushed with just enough force to start it moving across a floor and the same force continues to act afterwards. The coefficient of static friction and sliding friction are 0.5 and 0.4 respectively. The acceleration of the body is
View SolutionA particle of small m is joined to a very heavy body by a light string passing over a light pulley. Both bodies are free to move. The total downward force on the pulley is
View SolutionA 20 kg monkey slides down a vertical rope with a constant acceleration of `7 ms^(-2)`. If `g = 10 m//s^(-2)`, what is the tension in the rope ?
View SolutionA block A of mass 2 kg rests on another block B of mass 8 kg which rests on a horizontal floor. The coefficient of friction between A and B is 0.2 while that between B and floor is 0.5. when a horizontal force of 25 N is applied on the block B. the force of friction between A and B is
View SolutionA man slides down a light rope whose breaking strength in `eta` times his weight `(eta lt 1)`. What should be his maximum acceleration so that the rope just breaks ?
View SolutionA string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by

View SolutionA mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is `mu`. The force of friction between the mass and the surface is :
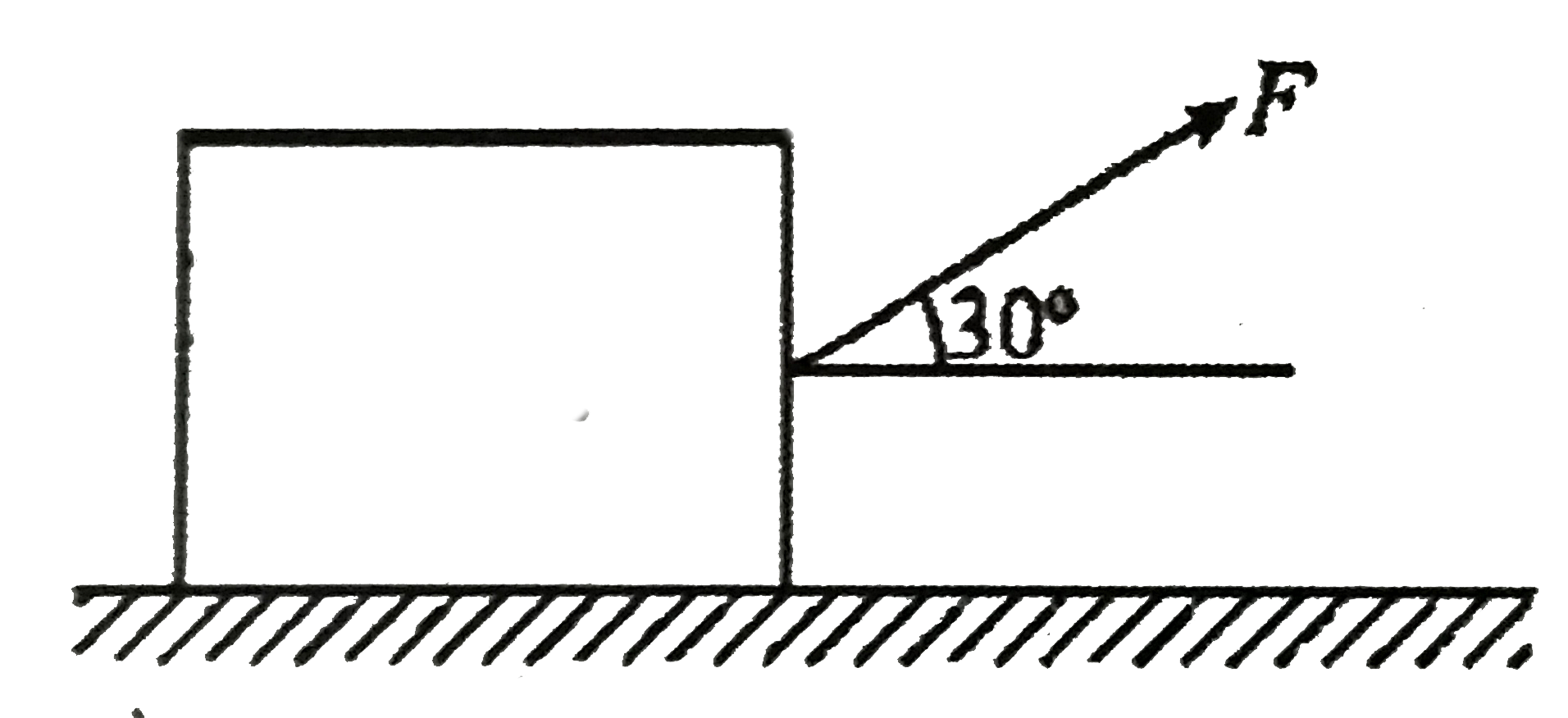
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA block of mass M = 4 kg is kept on a smooth horizontal plane. A bar of mass m = 1 kg is kept on it. They are connected to a spring as shown & the spring is compressed. Then what is the maximum compression in the spring for which the bar will not slip on the block when released if coefficient of friction between them is 0.2 & spring constant = 1000 N/m : (Take `g=10m//s^(2)`)

View SolutionIf Newton is redefined as the force of attraction between two masses (each of 1 kg) 1 meter apart, the value of G is :
View SolutionTwo weights `w_(1)` and `w_(2)` are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up at an acceleration g , the tension in the string will be
View SolutionThree weights are hanging over a smooth fixed pulley as shown in the figure. What is the tension in the string connecting weights `B` and `C` ?
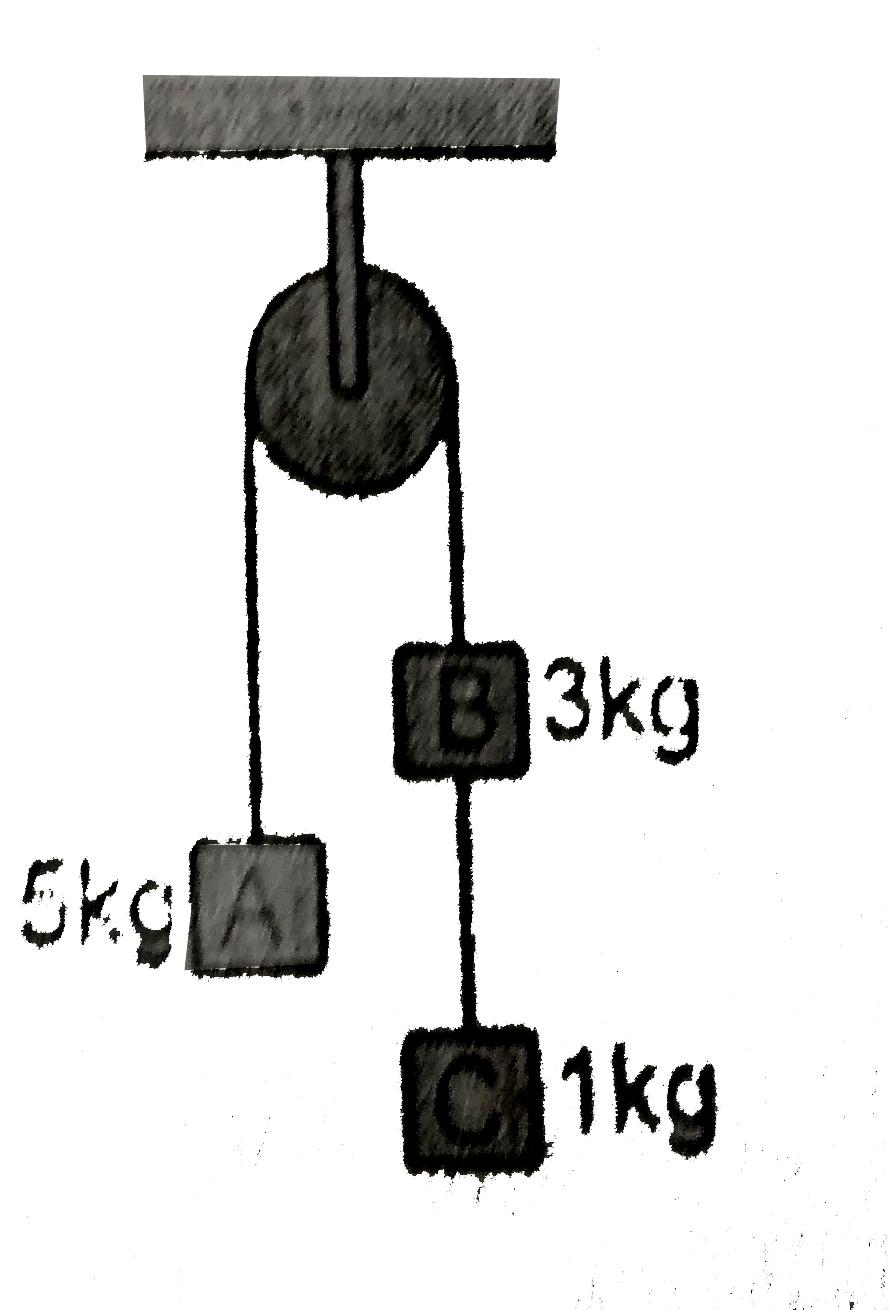
View SolutionFigure shown a wooden block at rest in equilibrium on a rought horizontal plane being acted upon by force `F_(1) = 10 N, F_(2) = 2 N`, as shown .IF`F_(1)` is removed , the resulting force acting on the block will be

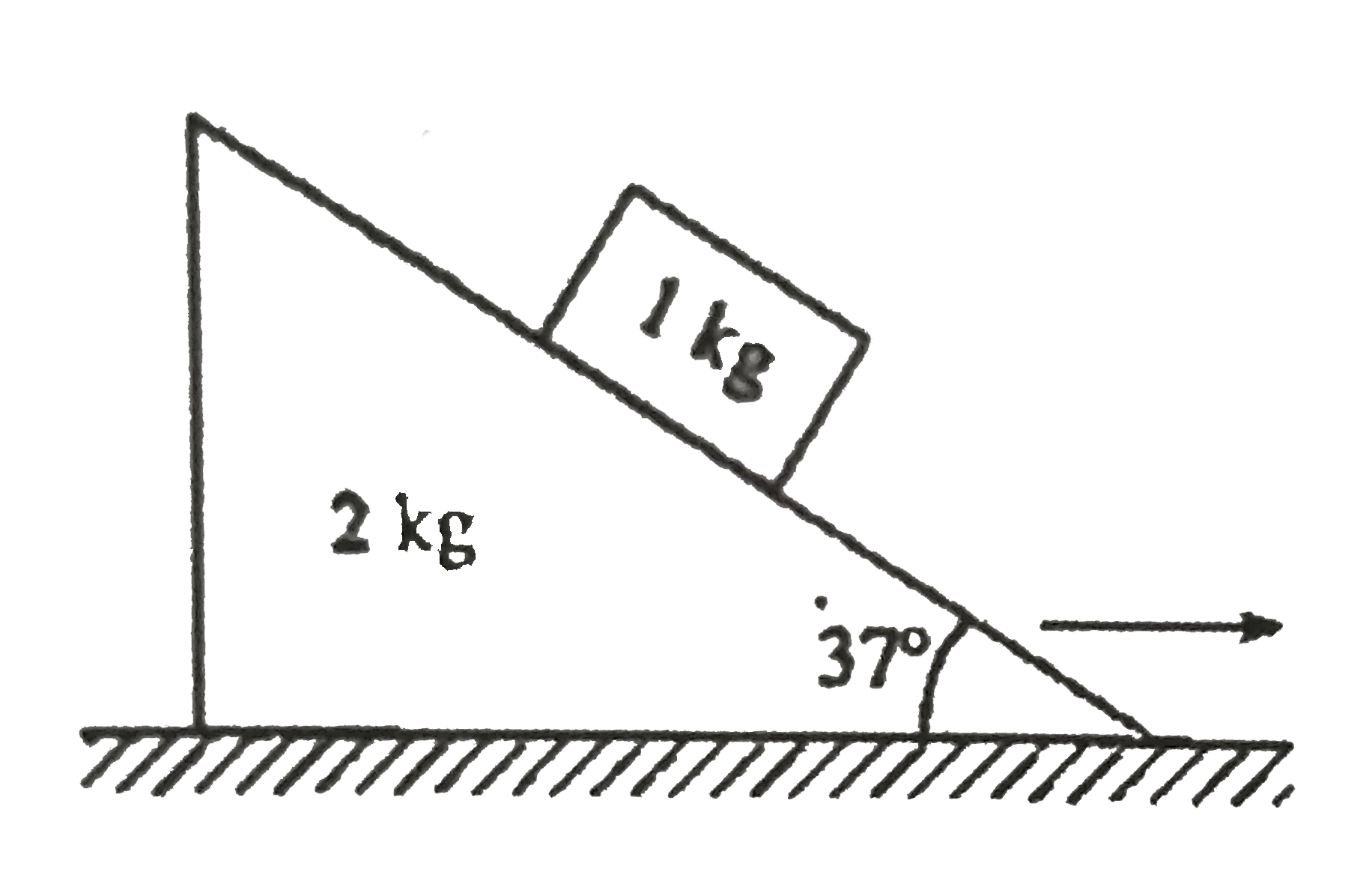
View SolutionFigure-2.162 shows a wedge of mass 2kg resting on a fritionless floor. A block of mass 1 kg is kept on the wedge and the wedge is given an acceleration of `5 m//s^(2)` towards right. Then :
View SolutionA man drags an m kg crate across a floor by pulling on a rope inclined at angle `theta` above the horizontal. If the coefficient of static friction between the floor and crate is then the tension required in the rope to start the crate moving is :
View SolutionIf the coefficient of kinetic friction be in above question then the initial acceleration of the crate will be :
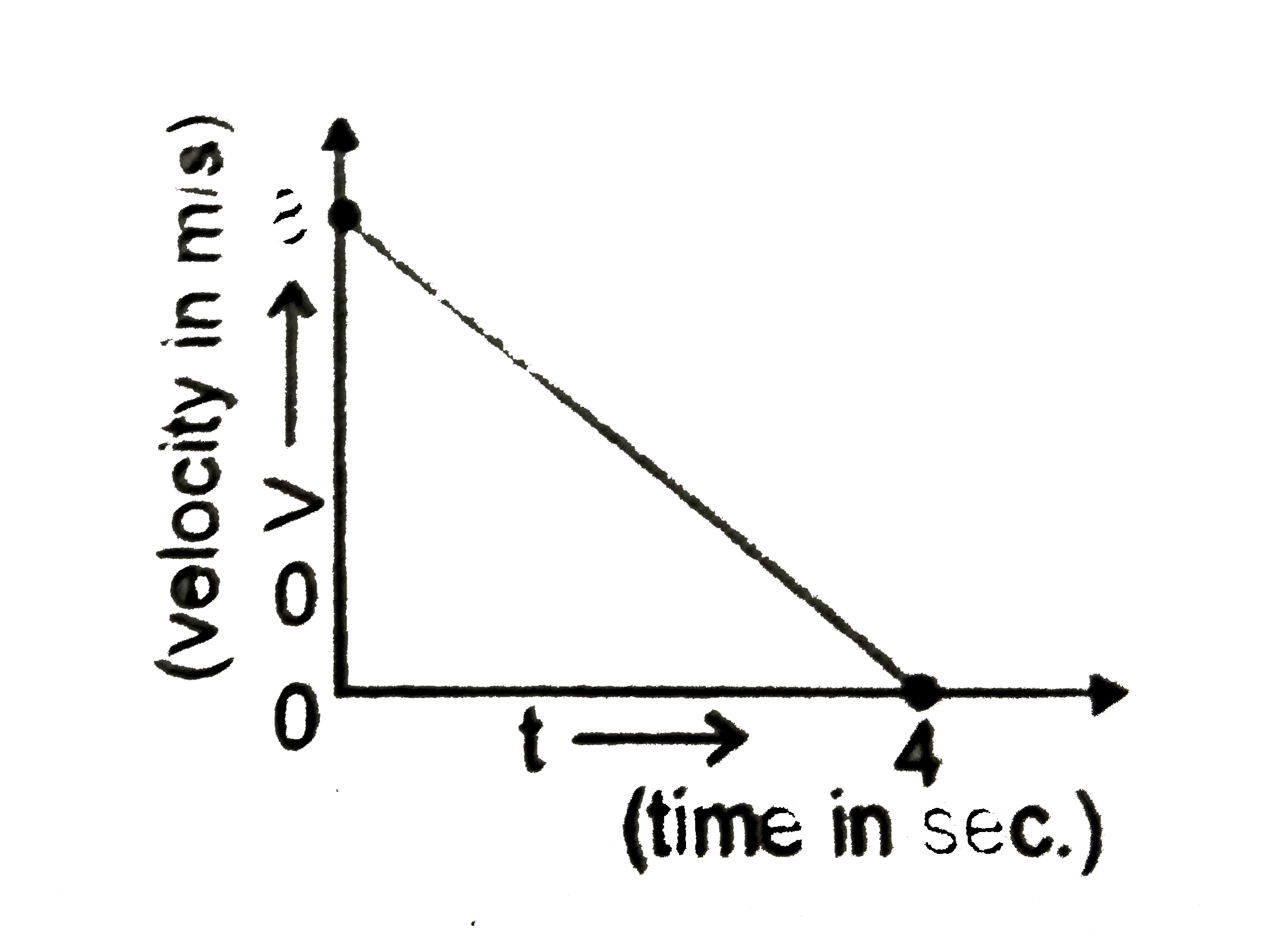
View SolutionA block of mass `2 kg` is given a push for a moment horizontally and then the block starts sliding over a horizontal plane. The graph shows the velocity`-` time of the motion. The co`-` efficient of sliding friction between the plane and the block is `:`
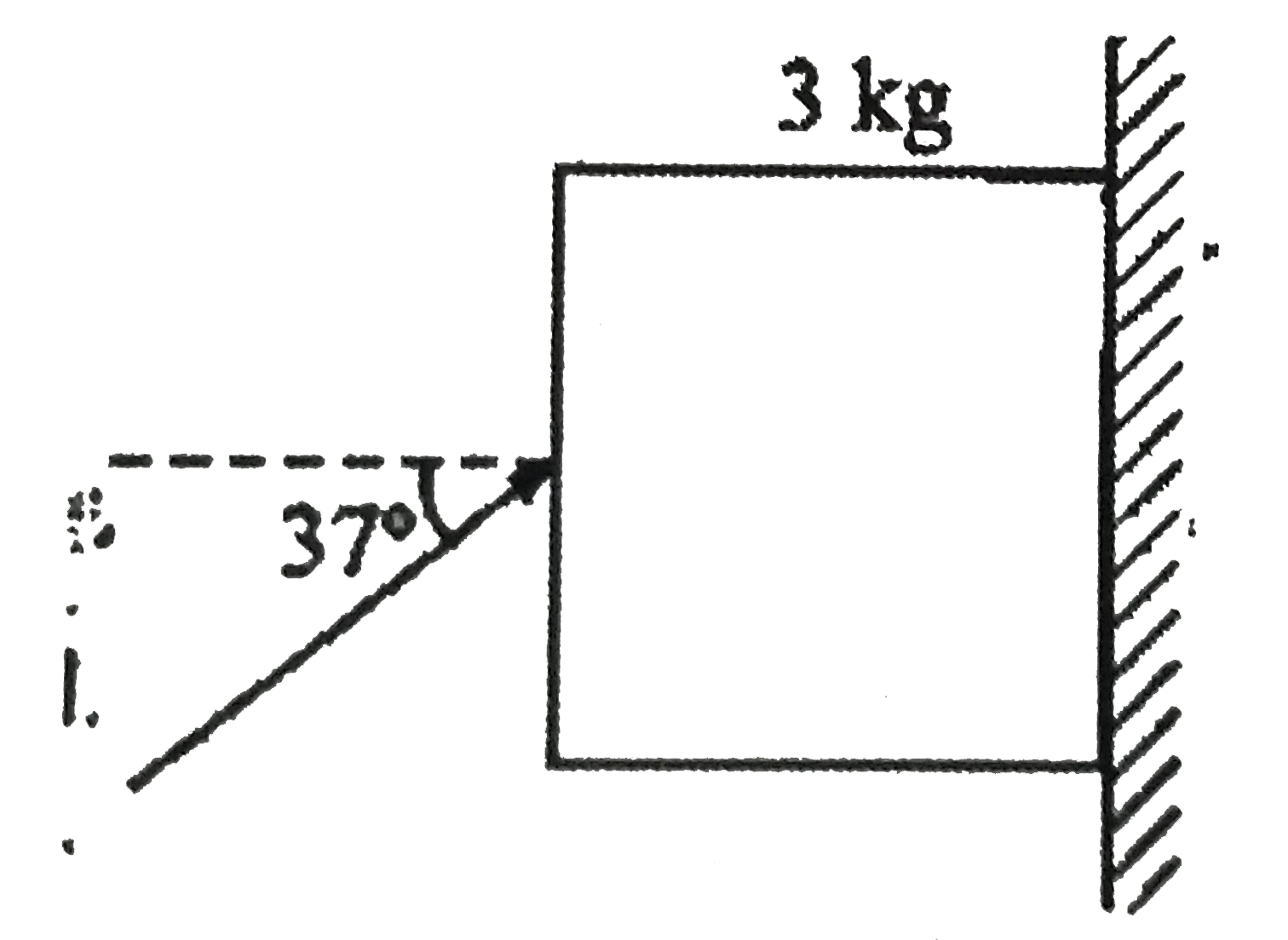
View SolutionA force of 100N is applied on a block of mass 3 kg as shown in the figure-2.164. The coefficient of friction between the surface and the block is 0.25.The frictional force acting on the block is: (Take `g=10m/s^(2)`)
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is `5m//s^2`, the frictional force acting on the block is…………newtons.
View SolutionA block of mass M on a horizontal smooth surface is pulled by a load of mass `(M)/(2)` by means ofa rope AB and string BC as shown in the figure-2.165. The length & mass of the rope AB are L and `(M)/(2)` respectively and BC is massless. As the block is pulled from AB= L t oAB = 0 its acceleration changes from :

View SolutionWhat should be the maximum value of M so that the 4 kg block does not slip over the 5 kg block : (Take `g=10 m//s^(2)`)

View SolutionThe direction of three forces 1N, 2N and 3N acting at a point,are parallel to the sides of an equilateral triangle taken in order. The magnitude of their resultant is:
View SolutionA body weighs 6gms when placed in one pan and 24gms when placed on the other pan of a false balance. If the beam is horizontal when both the pans are empty, the true weight of the body is :
View SolutionA 20 kg block placed on a level frictionless surface is attached to a cord which passes over two small frictionless pulleys,as shown in figure-2.167,to a hanging block originally at rest 1m above the floor. If the hanging block strikes the floor 2 s after the system is released, the weight of the hanging block is :
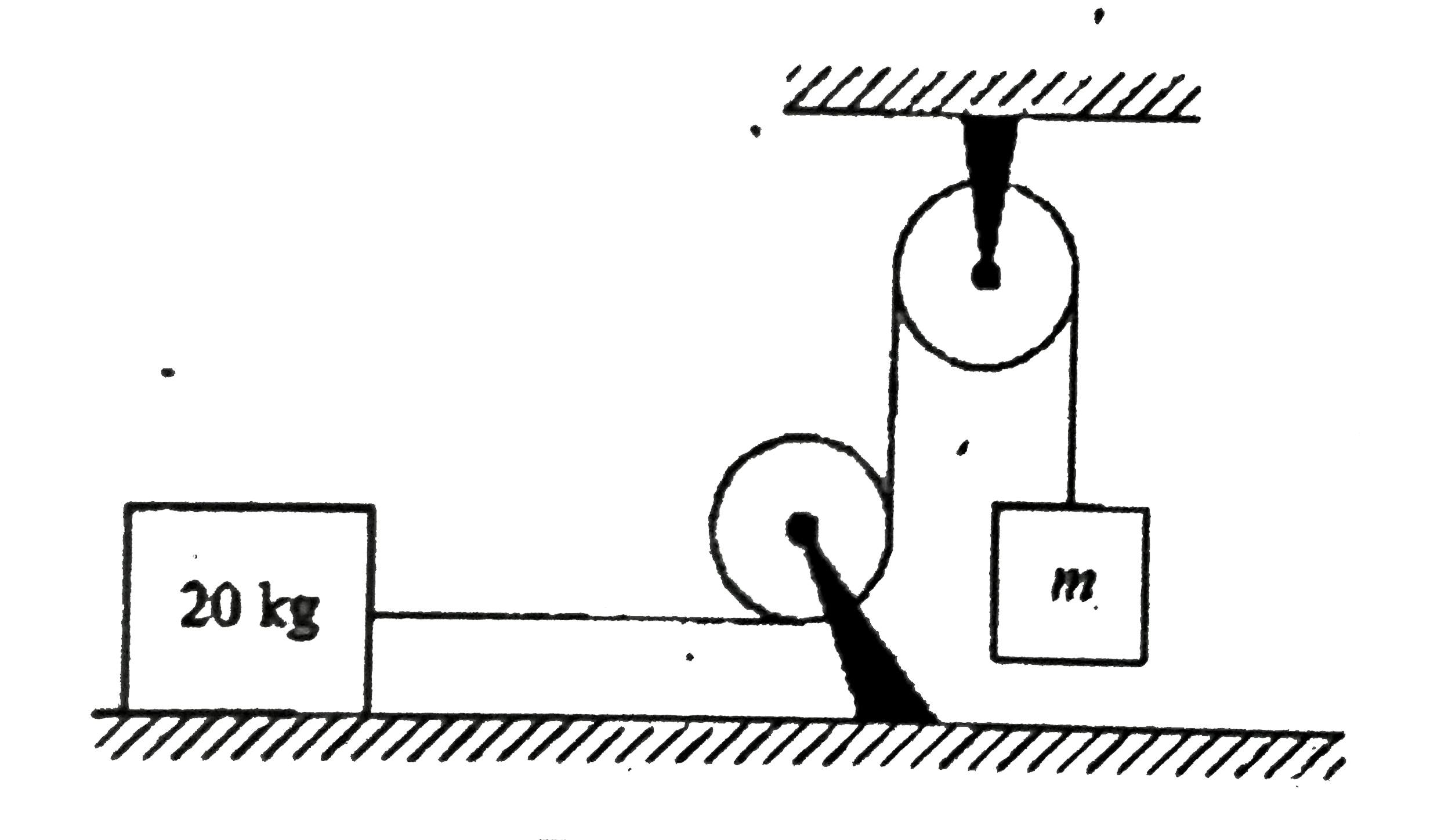
View SolutionFor the arrangement shown in figure-2.169, the tension in the string to prevent it from sliding down, is :

View SolutionA given object takes 3 times as much time to slide downa `45°` rough incline as it takes to slide down a perfectly smooth `45°` incline. The coefficient of friction between the object and the incline is :
View SolutionA stationary body mass `m` is slowly lowered onto a rough massive plat from moving at a constant velocity `v_(o)=4m//s`. On smooth surface. The distance the body will slide with respect to the plat from `(mu=0.2)` is:

View SolutionIn the arrangement shown, the pulleys are smooth and the strings are inextensible. The acceleration of block B is :
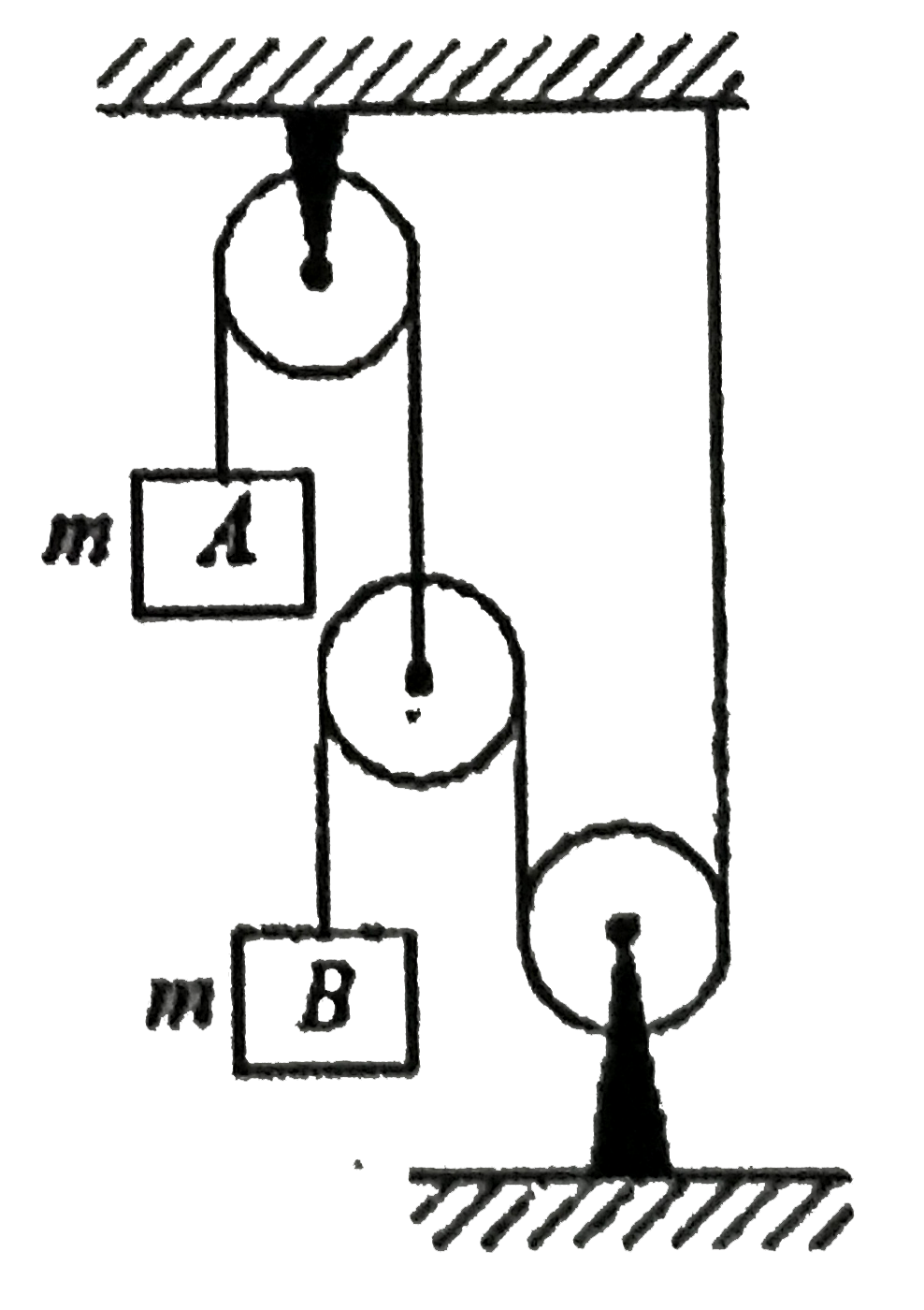
View SolutionAn empty plastic box of mass 9 kg is found to accelerate up at the rate of `g//3` when placed deep inside water. Mass of the sand that should be put inside the box so that it may accelerate down at the rate of `g//4` is :
View SolutionWith what minimum acceleration mass M must be moved on frictionless surface so that m remains stick to it as shown in figure-2.171. The co-efficient of friction between M & m is `mu` :
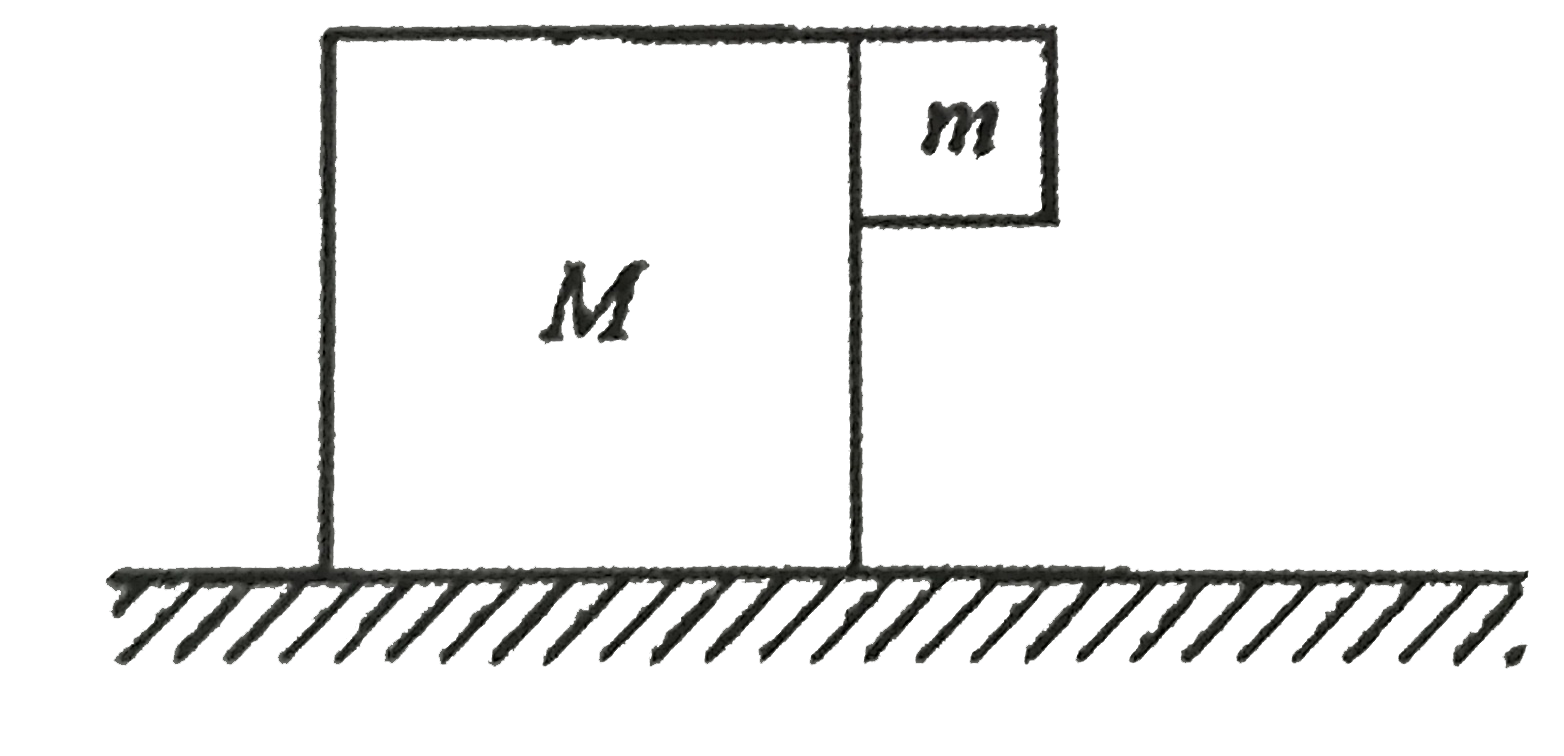
View SolutionThe coefficient of friction between 4 kg and 5 kg blocks is 0.2 and between 5 kg block and ground is 0.1 respectively. Choose the correct statement : (Take `g=10m//s^(2)`)
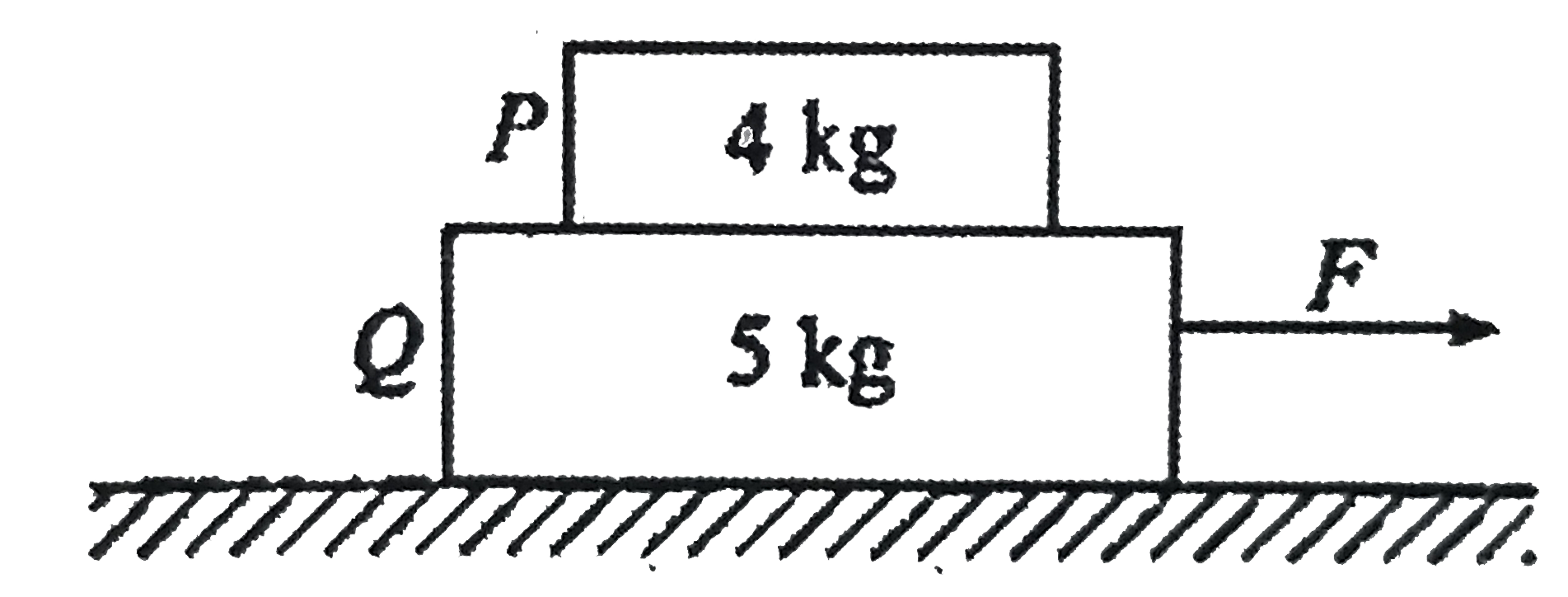
View SolutionFind the friction force between the blocks in the figure-2.173:
View SolutionA pulley is attached to one arm of a balance and a string passed around it carries two masses `m_(1)` and `m_(2)`. The pulley is provided with a clamp due to which `m_(1)` and `m_(2)` do not move. On removing the clamp, `m_(1)` and `m_(2)` start moving. How much change in counter mass has to be made to restore balance ?

View SolutionBlocks A and B have masses of 2 kg and 3 kg. respectively. The ground is smooth. P is an external force of 10 N. The force exerted by B on A is

View SolutionTwo blocks of masses `m_(1)` and `m_(2)` are placed in contact with each other on a horizontal platform. The coefficient of friction between the platform and the two blocks is the same. The platform moves with an acceleration. The force of interaction between the blocks is `:`

View SolutionA body of weight `w_1` is suspended from the ceiling of a room through as chain of weight `w_2`. The ceiling pulls the chain by a force
View SolutionA horizontal uniform rope of length L, resting on a frictionless horizontal surface, is pulled at one end by force F. What is the tension in the rope at a distance l from the end where the force is applied?
View SolutionA block of mass `m` slides down an inclined right angled trough .If the coefficient of friction between block and the trough is `mu_(k)` acceleration of the block down the plane is

View SolutionA ball is held at rest in position A by two light cords. The horizontal cord is now cut and the ball swings to the position B. What is the ratio of the tension in the cord in position B to that in position A?
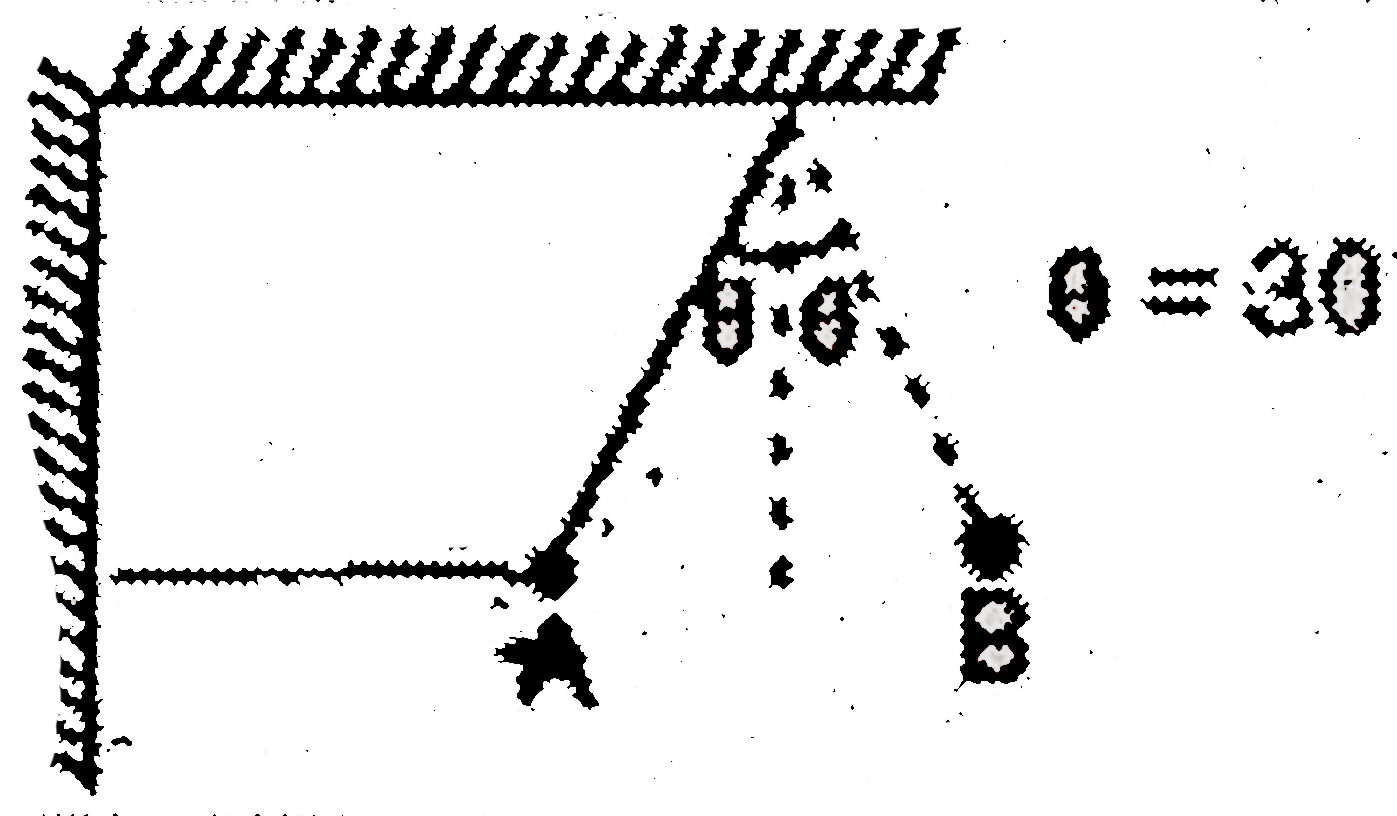
View SolutionA boy standing on a weighing machine notices his wight as 400 N. When he suddenly jumps upward the weight shown by the machine becomes 600 N. The acceleration with which the boy jumps up is : (Take `g=10m//s^(2)`)
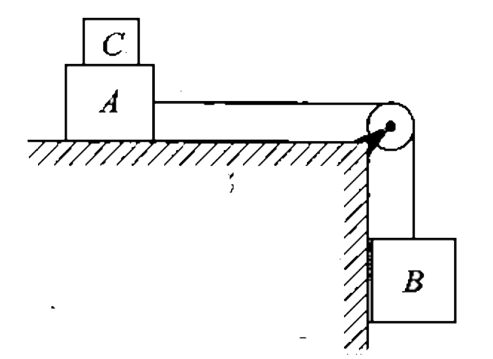
View SolutionTwo mass A and B of 5 kg and 6 kg are connected by a string passing over a frictionless pulley fixed at the corner of table as shown in figure-2.179. The coefficient of friction between A and the table is 0.3. The minimum mass of C that must be placed on A to prevent it from moving is equal to : (Take `g=10ms^(2)`)
View SolutionA heavy body of mass `25kg` is to be dragged along a horizontal plane (`mu` = `(1)/(sqrt(3))`. The least force required is `(1 kgf = 9.8 N)`
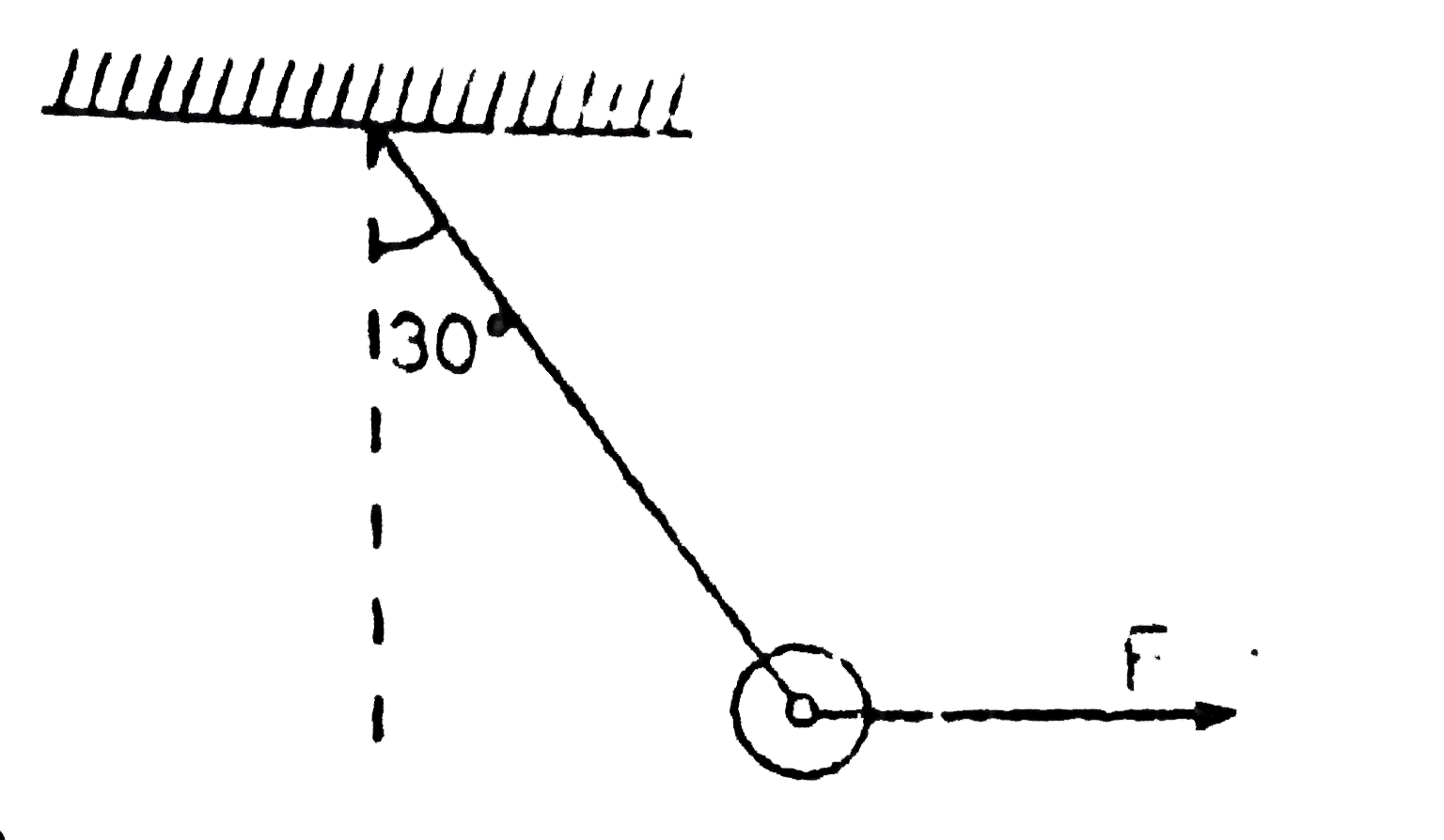
View SolutionA heavy particle of mass `1kg` suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle `30^(@)` with the vertical. The magnitude of the force F equals
 .
.
View SolutionThe human body can safely stand an acceleration 9 times that due to gravity which is `10 m//s^(2)`. The minimum radius of curvature with which a pilot may safely turn a plane vertically upward at the end of a dive, when the plane's speed is 720km/hr is :
View SolutionA 1 kg block is being pushed against a wall by a force F=75N as shown in the figure. The coefficient of friction is 0.25. The magnitude of acceleration of the block is:

View SolutionA block of mass 10 kg is suspended through two light spring balances as shown in figure

View SolutionThree rigit rods are joined to form an equilaterla triangle ABC of side 1 m. Three particles carrying charges `20 muC` each are attached to the vertices of the triangle. The whole system is at rest in an inertial frame. The resultant force on the charged particle. A has the magnitude.
View SolutionA rope of length L has its mass per unit langth `lambda` varies according to the function `lambda(x)=e^(x//L)`. The rope is pulled by a constant force of 1 N on a smooth horizontal surface. The tension in the rope at `x=L//2` is :

View SolutionWhat force must man exert on rope to keep platform in equilibrium : (Take `g=10m//s^(2)`)
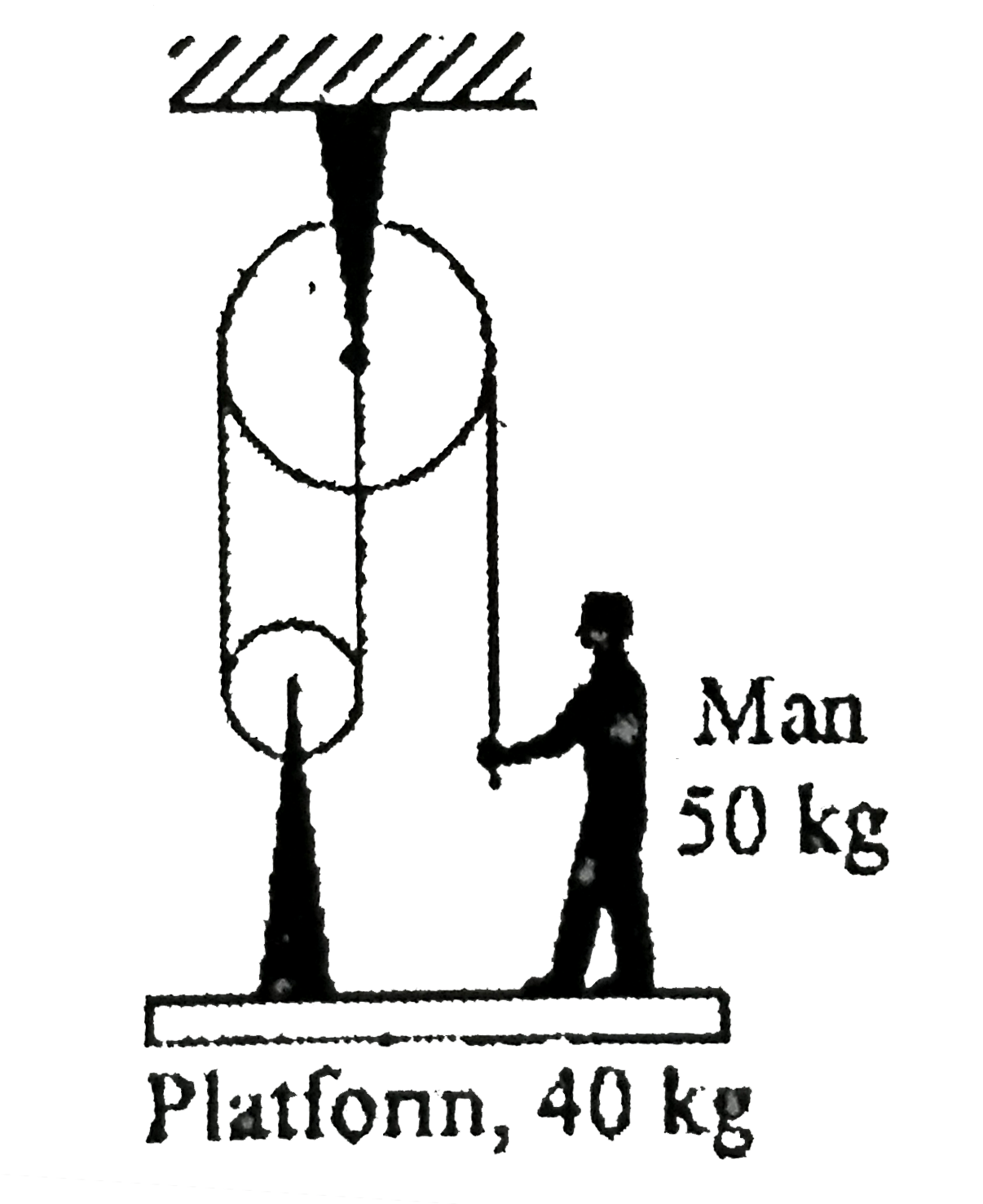
View Solution
Numerical MCQs questions and complete solutions for chapter NEWTONS LAWS OF MOTION of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11